直流微电网暂态自适应虚拟惯性控制策略及其参数可行域研究
2023-11-24张祥宇陈立威
张祥宇,陈立威,付 媛
(华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003)
0 引言
直流微电网作为大电网的有益补充之一,在具备灵活可控的功率调节能力的同时,无须考虑频率和功角稳定的问题[1-2],是目前针对新能源组网、吸纳分布式电源与负荷等应用场合的有效技术手段之一[3]。然而,高度电力电子化隐藏了微电网各端口的固有惯性,高新能源渗透率则容易诱发直流电压的频繁波动。“双高”特性为微电网的稳定运行带来了巨大的挑战[4],促使电压质量问题成为微电网的研究热点之一。
通过增加硬件设备可以改善直流微电网的暂态性能,但电解电容在功率密度和使用寿命等方面存在技术缺陷,超级电容器又难以克服经济性问题[5]。由此可见,硬件设施的研发仍缺乏突破性进展。而作为改善波形质量的另一途径,通过附加控制挖掘微电网隐藏惯性的方法已受到专家学者们的广泛关注[6]。文献[7-8]分别以电量和预测控制为切入点,通过动态调整蓄电池输出平抑直流电压波动,增强系统惯性。文献[9]则类比交流系统的转子运动方程建立惯性与电压变化率的函数关系,通过模拟电容外特性提高电网的电压支撑能力。然而,上述控制策略提供的有效惯量为常数,恒定的虚拟电容难以应对多变的系统工况,引入虚拟惯性在提供电压支撑能力的同时也会延长电压恢复的过程[10]。因此,微电网亟需灵活的惯性调节能力以进一步改善系统稳定性和动态性能。
目前,虚拟惯性自适应控制策略已衍生出多种形式。文献[11]通过向下垂控制中引入反正切函数来耦合系统惯性与电压变化率,在合理利用惯性裕度的同时还能防止下垂系数越限。但创新点主要聚焦在数学函数的优势融合,缺乏稳定性角度对虚拟惯性控制参数选取范围的研究。为消除线路阻抗的不良影响,文献[12]利用模糊算法改进自适应下垂控制器以实现不平衡功率在复合储能中的合理分配,但该研究缺乏对惯性水平的分析。文献[13]在传统灵活虚拟电容控制基础上综合考虑多个约束指标改进并设计虚拟电容值,对各指标的极限情况进行约束,然而虚拟电容设计过程忽略了直流电压恢复性能,且在回路中引入大量的模式切换环节可能会增加直流微电网失稳风险。为优化交流电网频率特性,文献[14]则沿袭虚拟电机控制的思路,通过类比的方法实现交直流参数间的相互映射,但虚拟惯性系数对频率波动影响的定量评估方法仍有待进一步研究。文献[15]以母线电压变化率为依据划分扰动等级,并借助高阶幂函数计算附加电容。但模式切换会为系统稳定性增加隐患,高阶幂函数随底数增长迅速,容易引发惯性过补偿,导致功率指令受限。
显然,现有的惯性自适应控制策略虽然就惯性裕度、电压波动程度等角度对惯量合理水平进行了一定的分析,但仍然难以满足系统在不同扰动下变化的惯性需求。直流微电网亟需能够在暂态过程中动态响应系统工况的灵活惯性支撑能力。另外,系统惯性和阻尼之间存在交互机理,惯性控制对直流微电网稳定性产生的影响也亟待评估[16]。换言之,惯性控制存在附加风险,控制参数的取值范围仍然有待研究。因此,还需要对附加虚拟惯性控制加以改进,进一步探究其暂态稳定性。
为了优化系统的动态响应能力,本文首先给出直流微电网的拓扑结构和端口控制策略。其次,利用电源和负荷侧的外特性曲线分析负荷变化后直流侧电量积累的暂态过程和稳态运行点的移动轨迹,并借助电量理论对下垂系数加以改进,提出一种能够依据系统运行工况投入可变虚拟电容的惯性自适应控制。然后,通过小信号建模和根轨迹分析明确控制参数对微电网稳定运行的影响。鉴于电量分析的局限性,通过引入极点配置的方法为控制参数的选取提供约束。最后,搭建五端直流微电网的仿真模型,验证本文所提控制策略的有效性。
1 直流微电网稳定运行电量分析
1.1 直流微电网的拓扑结构及固有惯性
大电网退出运行对于储能设备而言是最严苛的工作环境,此时储能设备需承担起短时间内维持系统内部功率平衡和电压稳定的职责。直流微电网系统拓扑如图1 所示,由风电机组、光伏电池组等新能源发电单元、以蓄电池为主的储能单元、交直流负荷等端口及其对应的电力电子换流器构成。图中:W_VSC 表示机侧电压源型变流器;PV_DC、B_DC 分别表示光伏电池组、蓄电池侧斩波电路;L_VSC 和L_DC分别为交、直流负荷侧变流器;Pw和Ppv分别为风电机组和光伏电池组模块向外输送的功率;Cw和Cpv分别为风电机组和光伏电池组模块的端口电容;PL1和PL2分别为直流负荷与交流负荷;Cdc和Cac分别为直流和交流负荷的端口电容;PB为蓄电池的输出功率;CB为储能端口电容。
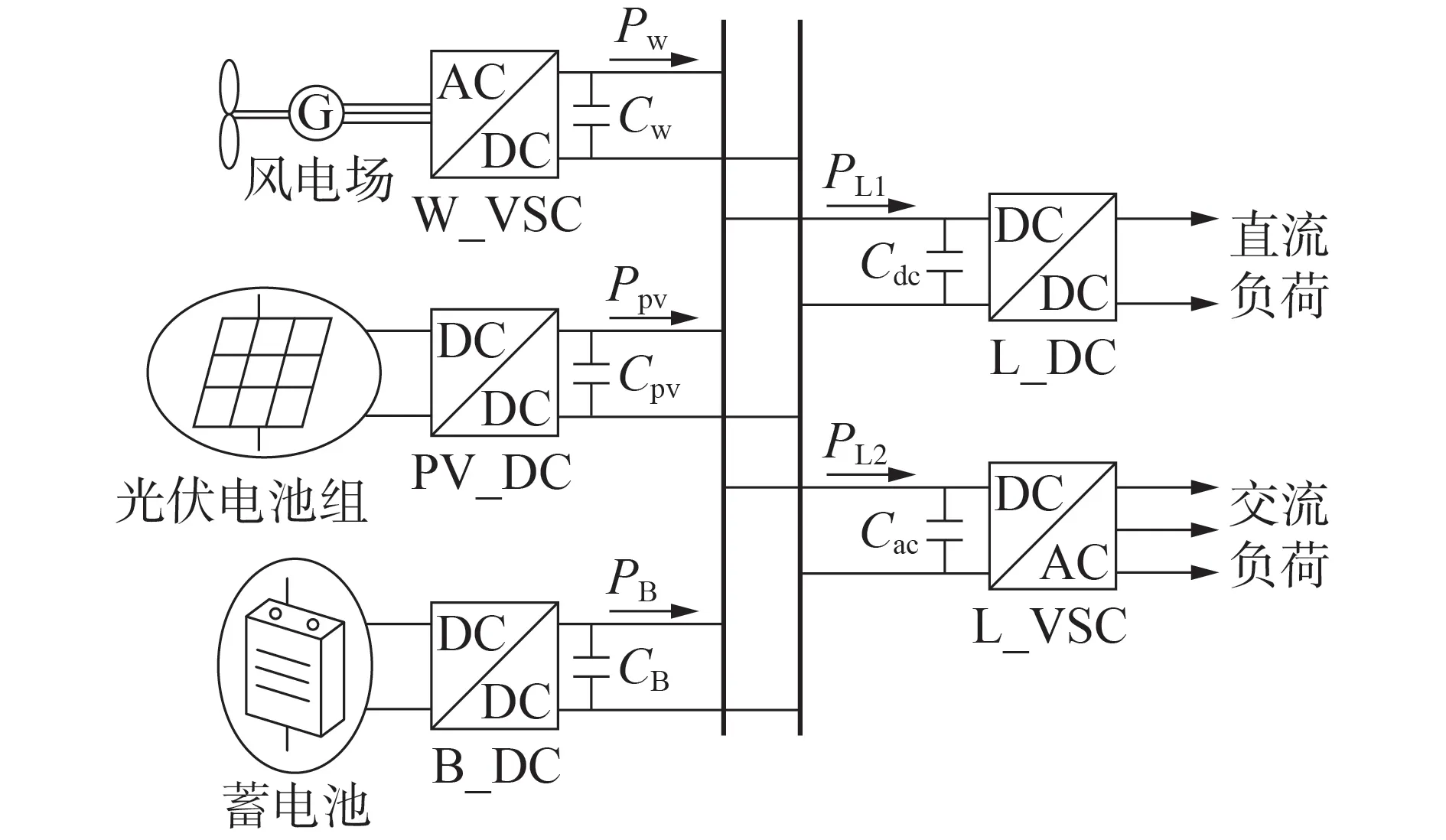
图1 直流微电网拓扑结构Fig.1 Topology structure of DC microgrid
其中,风电机组和光伏电池组分别通过机侧电压源型变流器W_VSC 和斩波电路PV_DC 向直流母线注入有功功率,两者通常采用最大功率点跟踪控制以充分利用风能和太阳能,在新能源富余时,储能设备配合负荷的就地消纳,能够减轻配电网向大电网的送电压力。交流负荷和直流负荷分别经由交直流负荷侧变流器L_VSC 和L_DC 与直流母线相接,通常运行于恒功率模式从直流微电网汲取相应的功率以满足用户的日常需求。储能单元通过斩波电路B_DC实现直流联网,通常采用下垂控制来平抑功率波动,实现维持直流侧电压相对稳定的效果。
当5 个端口输出功率相互平衡,系统不存在功率缺额时,微电网直流电压稳定。而当新能源或负荷发生波动时,直流电压也会随之变化。不同于交流系统,直流微电网用电压水平来描述整体的运行状态。系统惯性则表征为抑制直流母线电压波动的能力。通常采用系统惯性时间常数H0来表征,如式(1)所示。
式中:Wki为第i个并联电容器存储的电能;Ci为第i个并联电容器的电容值;Udc为直流电压额定值;SNci为第i个并联电容器的容量;n为并联电容器总数。直流惯性时间常数的物理意义为额定电压下并联电容器所存储的能量全部释放所需要的时间。
直流微电网借助大量换流器实现能量转换和功率交互,达到整合多种分布式发电单元的目的。然而,电力电子单元具有隔绝各端口耦合的作用,高度电力电子化为直流微电网引入低惯性的特征,最终埋下直流电压波动频繁且剧烈的隐患。
虽然惯性时间常数主要取决于直流电容,但各分布式发电单元直流侧并联电容并不足以有效抑制直流母线电压波动。考虑到储能单元具备功率双向吞吐的能力,若蓄电池能够实时追踪直流母线电压变化率并对其做出反馈,从而在直流侧模拟出电容吸发有功的效果,则对增强直流微电网的惯性,提高系统动态响应能力具有重要意义。
1.2 直流微电网稳定运行及电量分析
直流微电网在稳定运行期间内,交流负荷和直流负荷保持恒定,可将其合并成恒功率负荷单元,表征系统实际负荷总和,负荷总功率PLL=PL1+PL2。风电机组和光伏电池组向直流母线的注入功率虽然取决于风速和辐照度,但在短时振荡期间内近似保持不变,因此新能源发电单元同样可用恒功率源表示,其输出功率为PLS=Pw+Ppv。最终,参考文献[17]对直流微电网平均值等效模型的研究成果,可将恒功率负荷和新能源发电单元合并成一个等值负荷模型,用一个受控电流源表示,对应等值负荷PL=PLLPLS。蓄电池采用下垂控制弥补功率缺额,其直流侧电压参考值取决于输出电流,对应的斩波电路B_DC则可以等效为一个理想直流变压器,仅实现电压和电流增益的效果。因此,五端直流微电网的简化等效电路如图2所示。
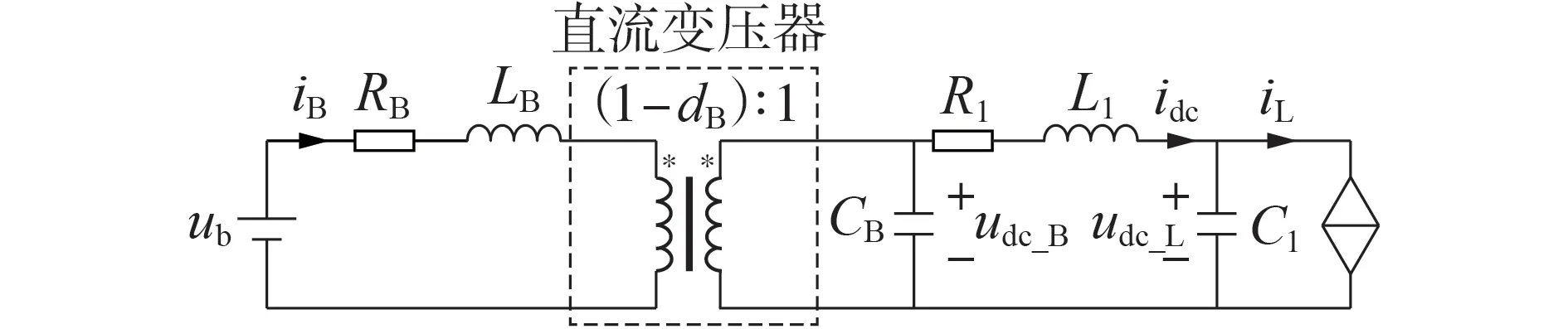
图2 微电网简化等效电路图Fig.2 Simplified equivalent circuit diagram of microgrid
其中,直流变压器为B_DC 简化模型,由非隔离型Boost电路平均值等效模型可知其变比为(1-dB)∶1,dB为占空比。直流变压器左侧为蓄电池侧:ub为蓄电池的直流电压;RB和LB分别为寄生电阻和滤波电感;iB为蓄电池的输出电流。直流变压器右侧为微电网及等效负荷侧:udc—B和idc分别为蓄电池换流器出口直流电压和电流;Rl和Ll分别为换流器和直流线路的等效电阻和电感;Cl为等效负荷直流侧的电容总和;udc—L为对应的负荷侧直流电压;iL为等效负荷对应的电流源输出的直流电流。
根据图2 所示的微电网简化等效电路和平均值等效模型,结合各端口控制原理以及基尔霍夫定律可得系统端口电压、电流以及功率方程分别为:
式中:udc—Bref和kB分别为蓄电池下垂控制的直流电压参考值和下垂系数。联立式(2)和式(3)可知,从回路电压角度来看,微电网稳定运行时蓄电池输出电流idc和直流电压udc—L之间满足一定的线性关系,即蓄电池在直流侧呈现出下垂的外特性,如式(6)所示。
而由式(4)和式(5)可知,从节点电流角度来看,系统稳定时负荷电流iL和直流电压udc—L之间满足双曲线的函数关系,且系统处于稳态运行时,蓄电池侧换流器端口输出电流与负荷电流相同。
稳定运行工况下,蓄电池直流侧和负荷侧外特性如附录A 图A1(a)所示。假设在初始时刻,系统的负荷特性曲线为L2,其与系统下垂特性曲线L1相交并存在A和B这2 个交点,即系统存在2 个可能的稳态运行点。
通过波动等效负荷完成负荷特性曲线L2的跃迁,即可进一步分析源荷两侧运行点的移动轨迹。其中,运行点B在负荷波动后会导致源侧和负荷侧运行点最终难以重合并引发系统失稳。相应地,运行点A在负荷波动后能重新到达新的稳定运行点,运行点移动过程分析见附录A。
此外,直流微电网在实际工程中常配备过压和欠压保护,直流母线电压波动受限于额定值±10 %的范围内。因此从系统运行与保护的角度来看,运行点B也并非稳态运行点。
综上所述,运行点A是直流微电网稳态运行工作点,系统维持稳态运行的必要条件为:
假设系统初始运行点直流电压为udc—L0,对式(2)—(5)附加小偏差量并做线性化处理,整理成矩阵形式后可得:
将式(8)中的系统状态矩阵用A表示。李雅普诺夫第一方法表明,系统大范围渐进稳定的充要条件是状态矩阵A的所有特征根都具有负实部。对于本文简化的系统而言,该条件可等效为状态矩阵A的迹为负,行列式为正,即:
将式(8)、(9)经过移项、变形和整理后可得:
其中,式(11)与式(7)等价。因此,系统能保持稳定的条件如式(10)所示。为了从电量角度诠释维持微电网稳定的充要条件,推导系统电量稳定判据,将式(10)两边同乘以直流电压udc—L,并在[t0,t1]内做关于时间的定积分,其结果如式(12)—(14)所示。
式中:Req=Ll/[Cl(Rl+kB)],表征蓄电池侧等效电阻;QB和QL分别为蓄电池和负荷侧在时间段[t0,t1]内积累的总电量。结合附录A 图A1的分析可知,直流微电网在负荷波动时从原始运行点逐渐偏移到新稳定运行点的过程实质上是蓄电池、负荷以及直流电容充放电动态平衡的过程。若能对蓄电池的输出加以调整改进,使其积累电量在暂态过程中响应电压的变化,则能在蓄电池侧虚拟出可控的直流电容,从而缓解新能源接入情况下直流微电网缺乏惯性的现象。
2 暂态自适应虚拟惯性控制
通过摇摆下垂曲线影响电源功率输出,进而模拟电容动态响应的恒定虚拟电容(invariant virtual capacitor,IVC)控制已取得大量成果。研究表明,借助虚拟电容能够显著缩小母线电压变化率,改善微电网的动态性能。但由于惯性补偿量为常数,在系统控制参数选取不当时,可能会引发系统惯性过补偿的问题。
考虑到蓄电池具备灵活的功率调节能力,若能使其输出响应直流母线电压的波动情况,进而在源侧模拟出可变电容,则能为直流微电网提供灵活的惯性支撑能力。本文基于暂态电量的研究对下垂控制加以改进,将下垂系数调整为:
式中:电压偏差项Δudc—L=udc—Bref-udc—L,表征系统直流电压偏离额定电压的程度;k1和k2分别为虚拟电容系数以及虚拟电容自适应系数,分别表征本文所提控制策略提供的IVC 和可变虚拟电容的大小。分析式(15)可知,下垂系数附加项为电压微分项的非线性叠加,不会对系统的稳态参数造成影响,本文所提的暂态自适应虚拟惯性控制属于自适应虚拟电容(adaptive virtual capacitor,AVC)控制,其优化仅针对负荷波动后的暂态过程。AVC 控制框图可用图3表示。图中:T1—T3分别为3 个一阶惯性环节的时间常数;kp和ki分别为电流内环比例和积分系数。

图3 AVC控制框图Fig.3 Block diagram of AVC control
从图3 可以看出,AVC 控制需要在下垂系数中引入电压和电流微分项,为了防止输入信号在采集过程中被高频干扰信号淹没,本文参考文献[3],在搭建仿真控制模块时,利用高通滤波器代替微分和滤波环节来避免波形失真。
为了对AVC 控制进行电量分析,将改进的下垂系数代入式(13),可知下垂控制经过修正后,蓄电池侧在时间段[t0,t1]内积累电荷增量ΔQB为:
可以看出,储能单元下垂系数的附加项会影响直流电源侧电量积累,并最终呈现出附加电容的控制效果,其具体数值为:
由于式(1)难以满足电容补偿控制下系统惯性分析需求,现通过补充虚拟电容的形式将端口换流器控制模式的影响纳入直流惯性时间常数的考量并加以补充改进,可知AVC 控制下,系统的惯性时间常数HAVC表达式如式(18)所示,这也是控制模式和控制特性在直流电网惯性分析中的一种体现。
式中:SN为直流电容额定容量之和;H0为直流微电网的固有惯性。结合式(17)可知,本文附加的虚拟电容值可划分成两部分,分别为IVC 项k1和可变虚拟电容项-k2Δudc—Ldudc—L/dt。其中,IVC 可为微电网提供恒定的惯性支持,提高系统整体惯性水平;可变虚拟电容的符号则取决于直流电压及其变化率的相对关系,从而为惯性控制引入自适应性。
由式(17)可知,虚拟电容的实际取值在数学上呈现出马鞍面的特性。虚拟电容同直流母线电压及其导数的函数关系曲面图如附录B 图B1 所示。图中,k1=0.3,k2=0.5。
按照前文定义电压偏差Δudc—L=udc—Bref-udc—L,当直流母线电压低于额定值时,其值符号为正;反之则符号为负。若同时引入直流电压的导数及其偏差项作为坐标,则可将附录B图B1划分为4个象限,分别表征微电网4种不同的运行工况。
附加虚拟电容值与系统运行工况的对应关系见附录B 图B2 和表B1,由图B1 可知,若直流电压偏差项Δudc—L和微分项dudc—L/dt同号,则对应运行工况1和运行工况3,分别为直流电压逐渐向额定值偏移的2 种运行工况。为减小电压偏差,提高波形质量。此时虚拟电容自适应项为负值,即可变虚拟电容Cvir 若直流电压偏差项Δudc—L和微分项dudc—L/dt异号,则对应运行工况2 和运行工况4,分别为直流电压高于额定值且持续升高及直流电压低于额定值且持续减小2 种电压偏离运行工况。此时系统的实时需求为缩小电压变化率,减缓电压的波动程度。对应自适应项为正值,可为系统提供额外的惯性,即可变虚拟电容Cvir>k1,有助于进一步阻止直流电压偏离额定值,正好吻合系统的惯性需求。 与IVC 控制相比,本文提出的AVC 控制应对不同工况时更具备惯性灵活性。然而,虚拟惯性存在附加风险,虚拟电容数值的选取又完全由系统控制参数决定,不合理的参数选取方式势必会影响负荷波动时微电网的暂态特性,甚至可能危及系统的稳定性。因此,有必要对控制参数的选取加以研究。本文通过引入控制理论的分析方法为惯性参数的选取提供约束,并给出其稳定取值区间,实现控制参数的优化设计。 本文在研究蓄电池侧换流器B-DC 的端口特性时,忽略其功率损耗,仅考虑换流器两侧端口电压和电流的增益。由图2可知: 将改进后的下垂系数代入式(2)并对式(2)—(5)以及式(19)、(20)在稳态条件下做小信号分析,经过化简后得到小信号模型如附录C 式(C1)—(C4)所示。以此为基础可推导各参数扰动量之间的函数关系如附录C 式(C5)—(C14)所示,结合图3所示的控制简化框图,通过线性叠加可得AVC 控制的小信号框图如附录C图C1所示。 根据小信号框图可推导AVC 控制下系统直流电压Δudc—B与电流Δidc间的闭环传递函数ξTF为: 式中:G1为AVC 控制的传递函数;Gid、Gii分别为蓄电池输出电流小扰动ΔiB与占空比小扰动ΔdB、蓄电池换流器端口电流小扰动量Δidc之间的传递函数;Gud、Gui分别为负荷侧直流电压小扰动Δudc—L与ΔdB、Δidc间的传递函数;Gpi为电流环传递函数;Gld为蓄电池输出电流参考值的小扰动量与负荷直流电压参考值小扰动量间的传递函数。 由式(21)可知,系统的元件参数、运行参数及控制参数都会对直流微电网的稳定性及动态性能造成影响。为进一步探究参数选取的适宜范围,首先需要识别对系统运行影响较大的关键参数。 特征根sn对参数kj变化的灵敏度可用特征根灵敏度量化,其定义为[18]: 结合式(21)、(22)可计算直流微电网控制参数和系统参数的特征根灵敏度,其具体计算结果见附录D 表D1。由表可知:等效电抗和电容主要影响特征根的实部,对应微电网运行稳定性;而比例积分参数则主要影响特征根的虚部,对应微电网的动态性能。由于本文仅关注控制参数的选取范围。在不改变系统元件参数的前提下,为了确定AVC 控制的控制参数选取范围,首先需要排除电流环中比例积分参数的影响。 由附录C图C1可知电流环传递函数ξPI为: 按照控制器的设计原则,系统开关频率应为电流环带宽的5~10 倍以确保微电网具备良好的动态特性[19]。本文搭建的仿真采用脉宽调制脉冲频率为7 650 Hz,电流环的比例系数取0.01,积分系数取100,电流环幅频特性见附录E 图E1。此时电流环的带宽为1 273.2 Hz,为开关频率的1/6左右,符合控制器的要求。 为了明确系统惯性参数的取值范围,首先需要评估微电网对惯性的需求。目前,我国关于直流电网惯性要求的标准规定尚未完善,但沿用直流系统研究发展的思路,通过借鉴交流电网的运行经验有助于确定系统对附加惯性的需求。 由式(2)可知,蓄电池端口电压变化量Δudc—B与其直流侧输出电流变化量ΔiB之间满足如下关系: 考虑直流电压波动范围并利用暂态期间的电压变化率的平均值代替瞬时值,对式(24)经过附录F式(F1)—(F3)的变形和整理即可得到直流微电网电容需求近似值为: 式中:Cn在数值上等效为实际电容及虚拟补偿电容之和;Tn为暂态持续时间。 传统交流电网惯量充足,基本能够实现系统惯性响应时间尺度上的全覆盖,从而为原动机调整出力保留时间裕度。在直流电网中,下垂控制相当于交流系统内的一次调频,能保证系统在较短时间尺度内的动态响应[20]。因此,暂态持续时间Tn可以有针对性地参考同等规模交流系统惯性响应和一次调频的时间范围。 根据式(21)可知,虚拟电容系数k1仅存在于闭环传递函数的分子上,对系统极点几乎没有影响,故其取值完全取决于系统对惯量的需求。而虚拟电容自适应系数k2则同时影响闭环传递函数的分母项和分子项。因此,需要对参数k2与系统极点之间的关系加以研究,确保附加AVC 控制不会影响微电网运行稳定性。 考虑到2个一阶惯性环节的时间常数T1和T2数值较小且非常接近,可令时间常数T1=T2=T,得到与自适应系数k2相关的特征方程和参数根轨迹分别如附录G 式(G1)和图G1 所示。从图G1 可以看出,电容自适应系数增大的同时,微电网稳定性也随之迅速降低,甚至存在引发系统失稳的风险。 为了确保微电网的稳定性和动态特性,需要对极点进行配置。根据保留一定稳定裕度ε下阻尼比ξ不小于0.3的设计原则,极点应满足条件如下: 式中:λ为极点的实部;Ω为极点的虚部;ξmin为阻尼比最小值。分别在直流母线电压高于和低于额定电压的情况下考虑极端情况,并假定蓄电池直流侧输出电流最大值imax不超过额定电流的1.5 倍,且原固定下垂控制下直流母线电压偏差不超过其额定值的10 %。结合式(26)和附录A 式(A18)可得出自适应系数k2的取值范围为: 式中:θ为最小阻尼比对应的角度,即cosθ=ξmin,稳定运行边界除了与直流电流最大值和下垂系数有关外,还受设定的稳定裕度和惯性时间常数影响,结合式(27)—(29)可得自适应系数选取范围与直流电流的关系图如附录H图H1所示。 综上所述,在设计惯性参数时,首先需要确定自适应系数k2的取值以保证系统的稳定性,再根据直流微电网对惯性的需求,借助暂态持续时间确定系统等效电容近似值Cn,最后对恒定电容参数k1的取值范围加以限定,才能实现可控的惯性补偿。 为了验证AVC 控制策略的可行性和有效性,本文搭建了五端直流微电网的仿真模型,拓扑结构如图1 所示。其中,交流和直流负荷均采用恒功率控制,风电机组和光伏电池组则采用最大功率点跟踪控制,蓄电池通过采用不同的控制策略加以对比。IVC 控制可看做本文自适应系数k2置零的效果,且由式(15)可知:置零惯性参数即可置零AVC 中的下垂系数增量,AVC 控制将退化为固定下垂控制。因此,仿真过程中采用的固定下垂控制可以用惯性参数置零的AVC 控制等效。具体的系统参数和控制参数见附录I表I1。 AVC控制能够满足直流微电网在不同运行工况下灵活的惯性需求,进一步优化直流母线暂态电压质量。因此,有必要对系统暂态运行工况下电压波动情况加以仿真验证。 在仿真的初始阶段,风速设置为12 m/s,辐照度设置为1 000 W/m2,风电机组和光伏电池组分别输出最大功率19 kW 和20 kW。交直流负荷的初始值和波动情况见附录I 表I2,4 种运行工况下系统直流电压波动特性如图4 所示,相应的储能端口输出功率和虚拟电容变化情况见附录I图I1 —I4。 图4 暂态运行工况下电压波动曲线Fig.4 Voltage fluctuation curves under transient operation condition 结合电压偏差项和直流电压变化率的符号可知,运行工况1和运行工况3分别对应直流电压低于和高于额定值情况下的电压恢复过程;运行工况2和运行工况4 则分别对应直流电压高于和低于额定值情况下的电压偏离过程。 结合图4 和附录A 图A8 —A11 可知,电压恢复期间内,采用IVC 控制的蓄电池由于惯性最强,负荷突变后直流母线电压恢复的速度最慢。而采用AVC控制的蓄电池可以通过调整输出来加快直流电压恢复的速度,其暂态恢复时间甚至比固定下垂控制还要短。电压偏离期间内,IVC 控制和AVC 控制会向微电网附加额外的惯性,其暂态过程相较固定下垂控制得以延长。其中,AVC 控制的自适应项符号为正,故其电压偏离的暂态过程最长,而下垂控制不存在附加惯性,其暂态过程最短,会最先到达新的稳态。 综上所述,AVC 控制能够动态响应直流微电网运行工况的变化并改变虚拟电容的投入,从而实现延缓电压偏离以及缩短电压恢复时间的目的。 AVC 控制可划分成2 个部分,参数k1可为系统提供恒定的虚拟电容,提高微电网整体的惯性水平,参数k2则可以动态调整附加虚拟电容值以满足系统动态的惯性需求。因此,有必要对AVC 控制参数在不同取值下的微电网的惯性特性加以仿真验证。 4.2.1 参数k1变化时微电网的惯性响应 在初始时刻,风电机组和光伏电池组分别向外输送约19 kW 和20 kW 的有功功率,交直流负荷分别为4 kW 和37.5 kW。直到在1 s 时,直流负荷突增至40 kW,并在3 s 时突减至37.5 kW,直流微电网的惯性响应特性曲线如图5所示。 微电网在1 s时突然出现约2.5 kW的功率缺额,在2 s 时又存在2.5 kW 的剩余功率。由于蓄电池均采用AVC 控制,可以通过调整输出来调节微电网动态响应。由图5 可知,固定k2=0.5 时,随着参数k1的增大,无论是母线电压的跌落还是恢复,微电网的暂态过程都有所延长,即恒定虚拟惯性参数k2可以提高微电网整体的惯性水平。 4.2.2 参数k2变化时微电网的惯性响应 在初始时刻,新能源端口采用最大功率点跟踪控制,风电机组和光伏电池组分别输出19 kW 和20 kW 的有功功率,且负荷运行情况与4.2.1 节所述初始时刻完全相同,这里不再赘述。在1 s 时,直流负荷由37.5 kW 突增为40 kW,并在3 s 时恢复成37.5 kW,采用不同自适应参数k2的情况下,微电网的惯性响应如图6所示。 图6 参数k2变化时微电网惯性响应Fig.6 Inertial response of microgrid when k2 changes 直流微电网在初始时刻运行于额定电压500 V,直至1 s 时发生直流负荷突增并出现2.5 kW 的功率缺额,经过0.5 s 左右的暂态过程后,系统在3 s 时又出现2.5 kW的瞬时剩余功率。 采用AVC 控制的蓄电池能够通过吸发功率改变系统的暂态响应。结合图6 中udc_B、Cvir波形可以看出,固定参数k1=3 的情况下,随着自适应系数k2的增大,电压偏离额定电压的暂态过程得以延长,而电压恢复的暂态过程则被逐渐缩短。由此可以看出,参数k2能够动态修改附加电容的大小,满足微电网实时的惯性需求。 直流微电网具备低惯性的固有特征,负荷的随机波动更会放大该缺陷,造成微电网母线电压频繁的波动。本文提出的AVC 控制能为系统提供动态电容抑制母线电压波动,提高微电网的惯性水平。 图7 为直流负荷在[37.5,44.5] kW 之间随机波动时,蓄电池采用固定下垂控制、IVC 控制以及AVC控制下微电网的动态响应。由图7 可知,蓄电池采用固定下垂控制、IVC 控制以及AVC 控制都可以平抑功率波动,维持直流电压稳定,但由于附加惯性能力的不同,采用固定下垂控制的微电网电压波动更加剧烈,而IVC 控制和AVC 控制都能够向微电网中投入虚拟电容,使直流母线电压波动更平滑。另外,相比于IVC 控制,采用AVC 控制的蓄电池的功率输出对微电网电压的波动更加敏感,能够更加快速地调整惯性功率,在延缓电压偏离的同时加速电压恢复,从而有效改善微电网的波形质量。 图7 负荷随机波动下微电网的惯性响应Fig.7 Inertial response of microgrid under random load fluctuation 总而言之,相较于固定下垂控制和IVC 控制,AVC控制更加适用于新能源渗透率较高以及负荷波动频繁的应用场合。 本文以直流微电网中的蓄电池为研究对象,针对IVC 控制灵活性不足,难以满足不同系统运行工况下变化的惯性需求问题,提出了一种AVC 控制策略。结合理论分析和仿真验证,得到了以下结论: 1)电量理论作为一种计算简便的辅助性研究手段,能够为暂态分析过程赋予更明确的物理意义,弥补数学分析方法重说明而少解释的问题,两者配合使用可以实现多角度的系统性能综合分析; 2)与惯性参数固定的IVC 控制相比,本文所提的AVC 控制能够根据微电网运行工况对可变虚拟电容进行实时调节,从而实现B-DC对系统的灵活惯性支撑,进一步优化微电网动态性能; 3)在分析直流微电网惯性需求的基础上,基于极点配置给出了自适应系数的量化取值区间,并进一步根据惯性需求和虚拟电容自适应项确定IVC 参数的取值,可以在实现系统稳定运行的同时具备良好的动态性能。 附录见本刊网络版(http://www.epae.cn)。3 暂态自适应控制参数分析
3.1 虚拟电容自适应控制小信号建模
3.2 暂态自适应虚拟惯性控制参数选取

4 仿真验证
4.1 暂态自适应虚拟惯性控制运行工况验证

4.2 参数k1和k2的控制效果验证
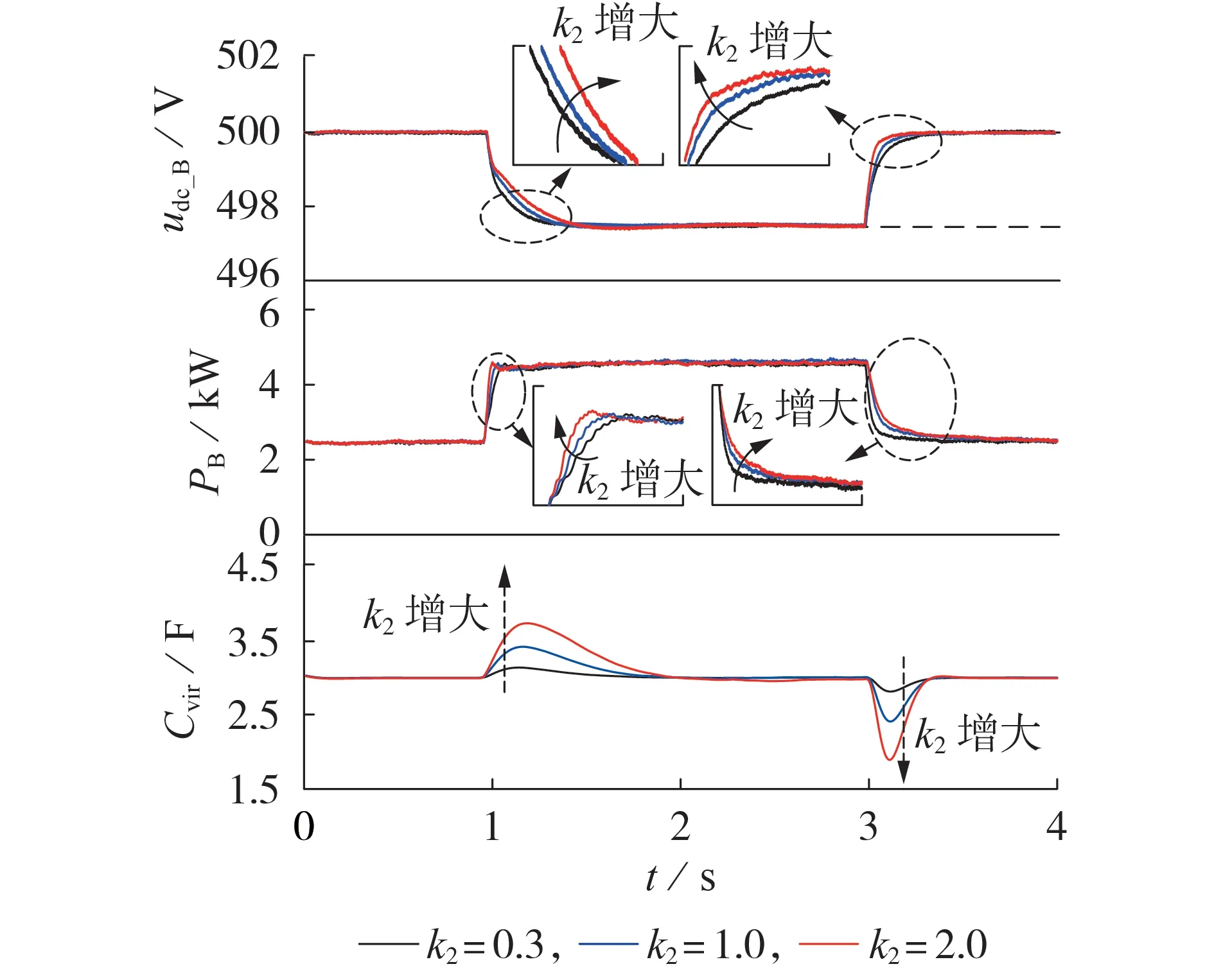
4.3 暂态自适应虚拟惯性控制的有效性验证
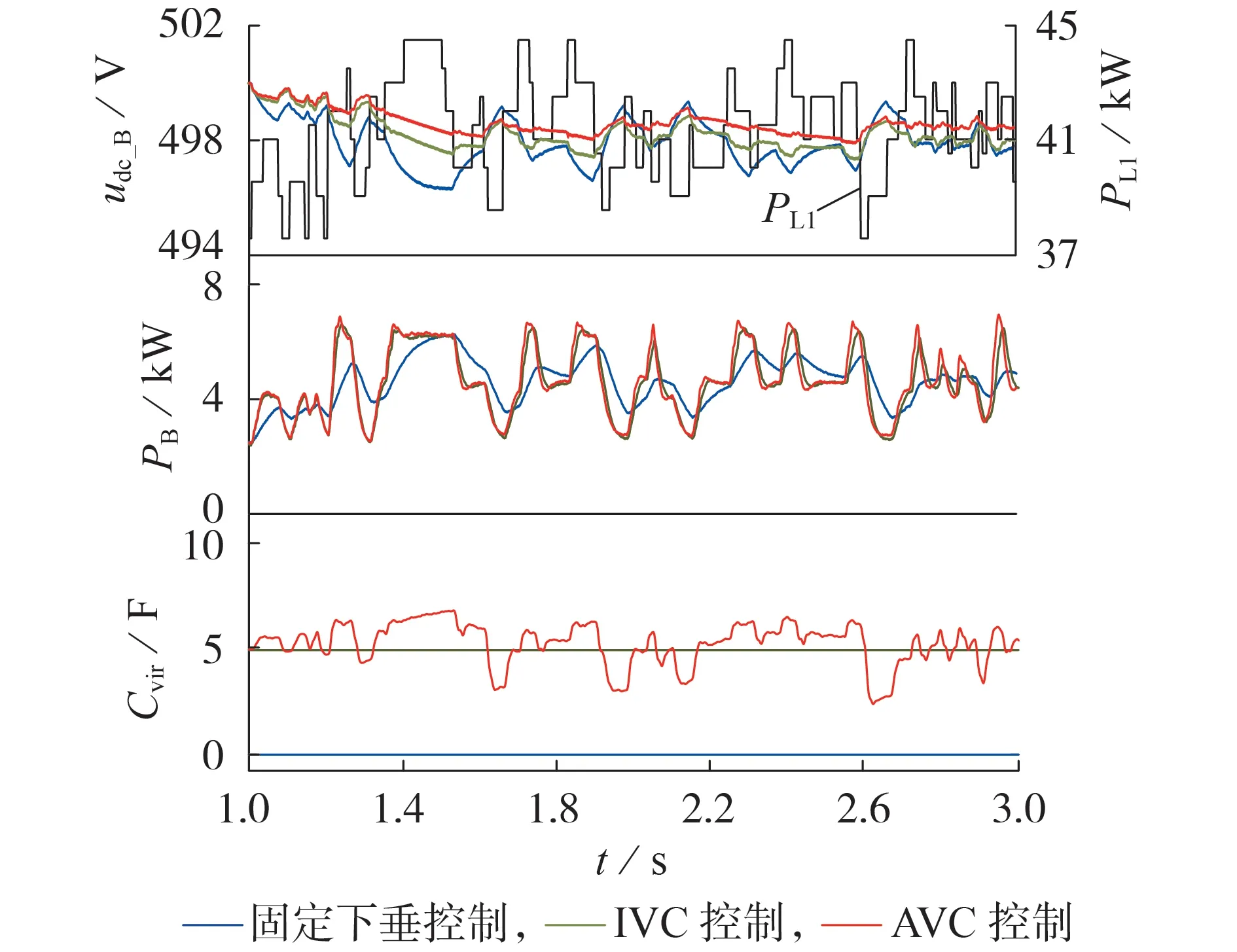
5 结论
