非轴对称五模超材料低频声波调控分析*

2023-11-23徐峰祥潘宇雄

应用声学 2023年6期

杜阔徐峰祥潘宇雄

(1 武汉理工大学现代汽车零部件技术湖北省重点实验室武汉 430070)(2 武汉理工大学汽车零部件技术湖北省协同创新中心武汉 430070)

0 引言

随着声波探测技术不断向低频段拓展，轻质高效的低频材料设计已成为亟待解决的难题。五模超材料是一种同时具备固体形态和流体属性的人造微结构材料[1]。在五模超材料的等效弹性矩阵中，只有体积压缩模态的特征值不为零，而另外5 个剪切模态的特征值均为零，这表明五模晶格周期结构具有显著的类流体力学特性[2]。在弹性波调控方面，五模超材料的能带结构表明，在波长大于晶格常数的频段内，存在与流体相似的线性纵波频散曲线。由这种周期性排列的类水五模胞元组成的声学超材料结构，在相当带宽内可以实现与水的完全匹配。五模超材料凭借薄层、宽带、可控模量各向异性等特性，使其在力学性能调控和声波调控方面均有非常大的应用潜力[3-4]。

2008年，Norris 等[5-7]基于变换声学理论验证了利用五模超材料制造声隐身斗篷的可行性，并论证了声隐身斗篷所需超材料的基本特性。2012年，Layman 等[8]将胞元结构设计与功能设计相结合，设计出一种可定制各向异性的二维斜蜂窝晶格五模材料结构，具有广阔的应用前景。2014 年，Aravantinos-Zafiris 等[9]提出一类非双锥型层状立柱结构五模式超材料，系统分析并优化了单胞的力学与声学性能。同年，国内武汉七一九研究所的学者制备了一种等效密度与水相近的二维环形铝基五模材料，并实验验证了该二维五模材料优异的声学隐身特性[10-12]。

在对超材料的研究中，通常认为带隙形成源于Bragg 散射机理和局域共振机理[13-14]。基于Bragg 机理的胞元，能带结构中的禁带往往在波长与晶格常数相当的较高频段处产生，这也意味着具有Bragg散射特性的胞元结构会因尺寸过大而失去应用价值[15-16]。Liu等[17]采用软橡胶包裹硬质基体构成局域共振单元，发现基于局域共振特性构建的胞元结构，其声子禁带可在波长远大于晶格常数的频段处产生。在水声调控方面，传统水声调控材料以引入气泡、空腔结构等方式增加入射波的能量耗散[18]。这样的材料对水声调控存在一定局限性，隔声工作频段越低，材料就越需要拓宽空腔尺寸、减小胞元弹性模量。考虑到材料在水下的工作环境和材料厚度的限制，Zhao 等[19]设计了一种类水的局域共振力学超材料，该材料在靠近低频声子禁带中心频率处具有超常的隔声特性。基于超材料在低频段的优异发挥，蔡成欣等[20]在三维双锥五模材料单胞的锥元两端处引入软质材料填充，使第一带隙相对带宽扩大了25倍，这为小尺寸五模超材料调控低频声波提供了可能。

随着声呐技术对低频声波感知范围的稳步扩大，为了规避低频声波探测，设计出具有低频宽带隙功能的轻质声学材料显得至关重要。传统五模超材料结构在低频段耦合作用弱、隔声频段窄的问题，现有五模超材料构型均集中在对对称单胞的分析，胞元构形差异不大，简单变换材料与相关结构参数对低频段单模区域和带隙提升很小，且均未探讨单胞对称性对能带的影响。为克服传统对称低频五模材料低频调控能力差的缺陷，本文在已有双锥单胞构型的基础上，设计了具有局域共振特性且含掺杂材料、飞镖型结构非轴对称单胞，探究了各单胞相关结构参数与材料参数对其频散曲线的影响。通过仿真分析，发现这些单胞在低频段不仅具有横波抑制而纵波传播的单模传输区域，而且具有阻止所有声波传播的声子禁带。相比于传统轴对称双锥单胞，设计的非轴对称单胞拥有频率更低、带宽更大的能带结构，改善了低频段薄弱的调控能力。这为用于低频声波调控的五模材料构型设计提供了思路。

1 非轴对称二维五模材料单胞构型及低频声波调控

1.1 非轴对称单胞模型

具有局域共振特性的传统轴对称双锥五模材料单胞(下文简称母胞)构型，由3 个对称双锥构成平面晶格，每3 个双锥结构由3 个扇形节点组成的节点圆连接。母胞晶格常数为a，节点圆半径为R，双锥宽为D，双锥轴向长为L。其中锥形填充区域由TC4钛合金作为硬质材料填充，扇形节点区域取硫化橡胶作为软质材料填充。

本文以母胞为设计模板，采用硬质材料区域不对称再设计和软质材料区域掺杂两种手段降低结构的对称性。通过引入飞镖型结构、掺杂材料的方式构建非轴对称单胞，各单胞结构如图1 所示，按引入飞镖型结构个数将单胞依次命名为A1、A2、A3，红色区域为掺杂材料填充部分。飞镖结构节点圆半径为r，锥角为α，为了更直观地分析降低对称性对能带结构造成的影响，仅控制图1 中目标硬质基体飞镖节点圆半径r、单锥锥角α与掺杂材料模量来改变各单胞的不对称程度，观察能带随参数的变化规律。

图1 非轴对称五模超材料单胞结构示意图Fig.1 Schematic diagram of the unit cell structure of non-axisymmetric pentamode metamaterials

1.2 低频声波调控

软质材料掺杂与硬质结构不对称布局会直接影响胞元在空间中的刚度和质量分布，从而改变结构的固有频率与单胞各阶共振模态。因此，不对称的引入会影响五模超材料的单模传输区域、声子禁带以及五模特性。为了探究非轴对称性对五模单胞能带结构和五模流体特性的影响，本文采用有限元方法，改变单胞局部的材料参数与结构参数，在Bloch 边界条件下扫描图2(a)中的灰色不可约布里渊区边界得到能带结构。母胞以图2(b)中六边形排列方式组成五模超材料结构，母胞结构参数如表1所示。

表1 轴对称母胞构型相关结构参数Table 1 Structural parameters related to axisymmetric mother cell configuration

图2 单胞简约Brillouin 区及其结构排列方式Fig.2 Unit cell parsimonious Brillouin region and its structural arrangement

其中硬质双锥填充TC4 钛合金，圆形节点区域部分填充硫化橡胶，选用与原软质填充材料杨氏模量差异较大的环氧树脂作为掺杂材料，各材料参数如表2所示。

表2 单胞结构填充材料的材料参数Table 2 Material parameters of cell structure filling materials

运用仿真软件依次沿路径XΓ、ΓM、MX对不可约布里渊区边界进行扫描，计算得到图3(a)～(d)所示的频散曲线。图中包含6 条能带，横坐标表示扫描的倒格子空间中布里渊区的波矢方向，纵轴表示所处的频率。图中标识的黑色矩形区域为第一带隙，位于此频段范围的声波将无法传播；灰色矩形部分为只允许纵波传输的单模传输区域。在对五模单胞的频散分析中可以发现，图3(a)所对应的传统轴对称单胞[21-22]单模区域频率范围约为250 Hz，禁带频段处于约700 Hz 的较高频率处，存在低频调控性能差的问题。对传统单胞进行非轴对称设计后，图3(b)中引入掺杂的胞元结构单模区域宽度提升了两倍；图3(c)中含单叶飞镖结构的胞元禁带中心频率从700 Hz 下沉至450 Hz 附近；与单叶飞镖结构单胞禁带相比，图3(d)含三叶飞镖结构的胞元禁带频段拓宽了约3.6 倍。非对称处理后的单胞能带结构的变化表明，降低单胞对称性可能获得超越传统对称单胞的优质单模宽带和声子禁带。

图3 五模单胞频散曲线图及掺杂母胞中A、B、C、D 点的振型图Fig.3 Pentamode unit cell dispersion curves and mode shapes of points A, B, C,and D in doped mother cells

为了观察到五模超材料单模区域频段内的机能，在其频散曲线原点附近处，选取了能带上的A、B、C、D四个参考点，参考点对应的单胞振型如图3(e)～(h)所示。在图3(b)的频散曲线中处于ΓX段的波矢方向为垂直方向，图3(e)中质点的振动方向与波矢平行，图3(f)中质点的振动方向与波矢垂直，同样的可以得到C、D处波矢方向与质点振动方向的关系，即A、C点对应纵波模式，B、D点对应横波模式。这意味着在灰色区域只允许纵波传播而横波被抑制，表征了五模超材料在这一频段区域的流体特性。

此外，为了体现五模超材料在禁带频域范围内的隔声效用，将图3(b)对应的单胞按20×5 的矩形数组进行阵列，并将阵列结构置于矩形水域中，建立的模型如图4(a)所示。对模型左端口处施加激励，在水域中声波通过五模结构后的传声损耗情况如图4(b)所示，掺杂母胞的传声损耗曲线在禁带的中心频率处存在两个较高的传递损失峰值，即结构能很好地抑制频段处于带隙中心频率附近的声波传播，说明此五模单胞阵列结构可起到较好的隔声作用。基于频散曲线中这两段区域的特性，五模超材料不仅可以在单模传输频段内利用自身的类流体特性实现声隐身功能，还能够在带隙频段范围内实现超常的隔声功能。

图4 五模材料水下隔声效用验证Fig.4 Verification of underwater sound insulation effect of pentamode materials

为直观比较各单胞声波调控性能的差异，令频散曲线中所求区域的频率上界为fT，下界为fl。绝对带宽为Abw=fT-fl，绝对带宽越大表示带宽性越好；相对带宽为Rbw=Abw/((fT+fl)/2)，相对带宽越大表示带隙低频性越好。对五模材料在单模传输区域的弹性波解耦能力可用五模品质因数(FOM=B/G)来表征，品质因数越大，表示体积模量B相对剪切模量G越大，纵波和横波之间越难以耦合。当五模品质因数FOM＞1000时，即所设计的五模材料结构具有较好五模特性，与理想五模材料一样能对声波进行调控，品质因数可由纵波和横波对应能带曲线斜率比值的平方求得[21]。图3(b)中掺杂母胞的第一带隙频率上界fT1=781 Hz，频率下界fl1=716 Hz，绝对带宽Abw1=65 Hz，相对带宽Rbw1=9%；单模传输区域频率上界fT2=629 Hz，频率下界fl2=21 Hz，绝对带宽Abw2=608 Hz，相对带宽Rbw2=187%，品质因数约为3640。引入掺杂材料后的母胞解耦了下端缠结的能带，使胞元具有更宽的单模传输区域和更低频的第一带隙，并保持了母胞的五模特性，这说明降低单胞对称性有助于改善单胞的能带结构。造成这种现象的原因可能是单胞在材料上的非轴对称的布置改变了空间中结构刚度和质量的分布，使得相应等效刚度和等效质量的比值向低频靠拢，进而产生了与传统对称单胞不同的频散曲线。

2 数值仿真结果及讨论

为了进一步探究单胞在材料与结构分布上的不对称程度对调控能力的影响，本节对图1 所涉及的3 种构型单胞进行能带结构计算，分析了可改变单胞不对称程度的参数对单模传输区域、第一带隙以及品质因数的影响规律。

2.1 硬质节点圆半径对能带结构影响分析

取0.2～1.6 mm 区间内8 个值作为硬质节点圆半径r，在其他材料参数和几何参数不变的情况下，单独改变虚线框内目标节点圆半径得到相关的数据进行计算处理，单胞硬质节点圆半径变化如图5所示。

图5 飞镖型非轴对称单胞硬质节点圆示意图Fig.5 Schematic diagram of dart type non axisymmetric single cell hard node circle

2.1.1 单叶飞镖单胞节点圆半径对能带结构影响

当引入一叶飞镖型结构时，单胞A1 能带结构随硬质节点圆半径r的变化如图6 所示，半径r越大，单胞A1 的非轴对称性越强。当r=1.6 mm 时，单胞A1的轴对称性程度最弱。随着半径的增加，单模传输区域上界频率fT2从279 Hz 降至251 Hz，绝对带宽Abw2减小了28 Hz。频散曲线中位于低频的能带解耦，第一带隙的频段活动范围从466～509 Hz下沉至380～492 Hz，绝对带宽Abw1增加了69 Hz，相对带宽Rbw1从8.8%提升至25.7%。相比母胞，单胞A1 第一带隙绝对带宽Abw1提升了56 Hz，相对带宽Rbw1提升了17%。

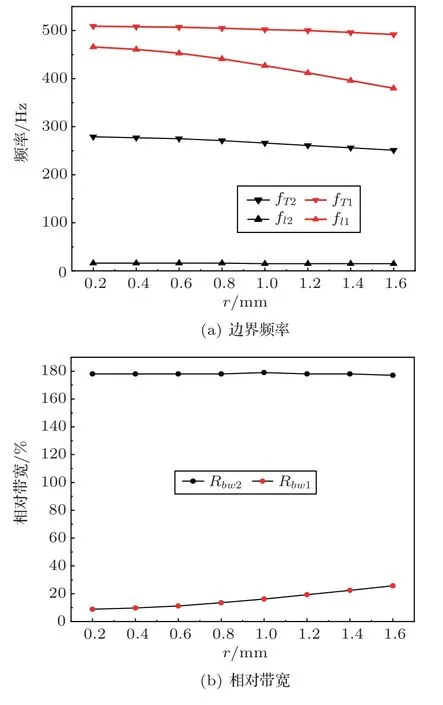
图6 节点圆半径对单胞A1 能带结构的影响Fig.6 Influence of node circle radius on band structure of unit cell A1

2.1.2 双叶飞镖单胞节点圆半径对能带结构影响

当引入两叶飞镖型结构时，单胞A2 能带结构随硬质节点圆半径r的变化如图7 所示。当r=1.6 mm 时，单胞A2 的轴对称性程度最弱。随着半径的增加，单模传输区域上界频率fT2从273 Hz 降至248 Hz，绝对带宽Abw2减小了25 Hz。第一带隙的频段活动范围从430～563 Hz 下沉至348～561 Hz，绝对带宽Abw1增加了80 Hz，相对带宽Rbw1从26.8%提升至46.9%。相比母胞，单胞A2第一带隙绝对带宽Abw1提升了157 Hz，相对带宽Rbw1提升了38%。

图7 节点圆半径对单胞A2 能带结构的影响Fig.7 Influence of node circle radius on band structure of unit cell A2

2.1.3 三叶飞镖单胞节点圆半径对能带结构影响

当引入三叶飞镖型结构时，单胞A3 能带结构随硬质节点圆半径r的变化如图8 所示。当r=1.6 mm 时，单胞A3 的轴对称性程度最弱。随着半径的增加，单模传输区域上界频率fT2从302 Hz 降至270 Hz，绝对带宽Abw2减小了31 Hz。第一带隙的频段活动范围从382～673 Hz 下沉至342～673 Hz，绝对带宽Abw1增加了40 Hz，相对带宽Rbw1从55.2%提升至65.2%。相比母胞，单胞A3第一带隙绝对带宽Abw1提升了275 Hz，相对带宽Rbw1提升了57%。

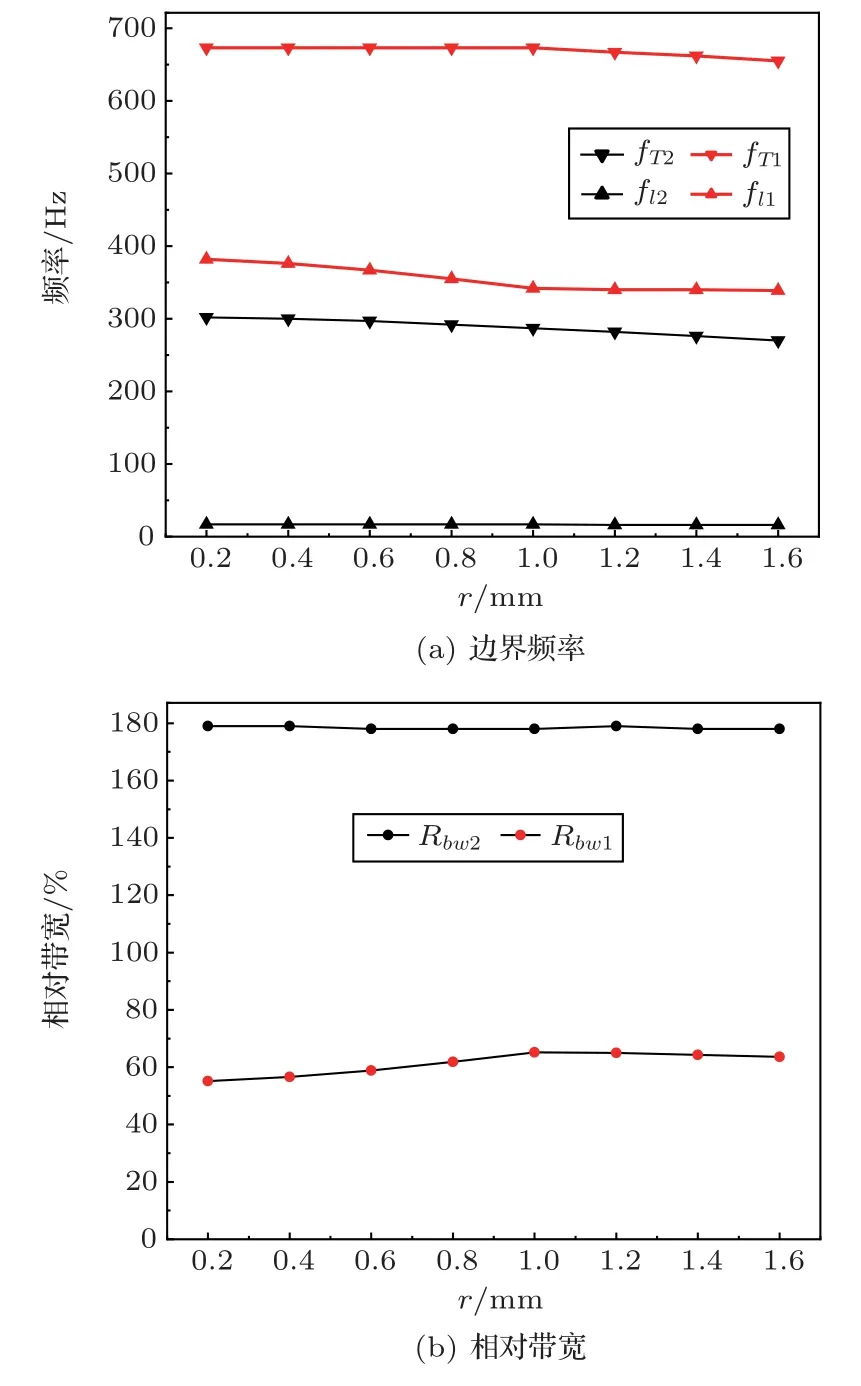
图8 节点圆半径对单胞A3 能带结构的影响Fig.8 Influence of node circle radius on band structure of unit cell A3

2.2 飞镖锥角对能带结构影响分析

对于引入飞镖型结构的单胞，飞镖结构中单锥角度α的改变也会影响带隙的分布。锥角α越大，单锥面积越大，单胞A1 的非轴对称性越强。取16°～44°区间内8 个角度作为硬质基元双锥锥角α，在其他材料参数和几何参数不变的情况下单独改变虚线框内两锥元的锥角α，观察能带结构变化，目标飞镖锥角变化如图9 所示。

图9 飞镖型非轴对称单胞飞镖锥角示意图Fig.9 Schematic diagram of cone angle of dart type non axisymmetric single cell dart

2.2.1 单叶飞镖单胞锥角对能带结构影响

在引入飞镖型结构的单胞A1 中，能带结构随锥角α的变化如图10所示，带宽性能与锥角α大体呈线性关系。当α=16°时，能带中第一带隙宽度极小，绝对带宽Abw1仅有5 Hz。随着锥角α的增加，处于低频的带隙逐渐解耦。当α=40°时，单模传输区域上界频率fT2从254 Hz 提升至289 Hz，第一带隙的频段上下边界从660～665 Hz 降至418～538 Hz，绝对带宽Abw1增加了115 Hz，相对带宽Rbw1从0.75%提升至25.1%。

图10 锥角变化对单胞A1 能带结构的影响Fig.10 The effect of cone angle variation on the band structure of unit cell A1

2.2.2 双叶飞镖单胞锥角对能带结构影响

对于引入飞镖型结构的单胞A2，能带结构随锥角α的变化如图11 所示。随着锥角α的增加，低频解耦的带隙带宽逐渐增大。当α=44°时，单模传输区域上界频率fT2从261 Hz 提升至319 Hz，第一带隙的上下边界从660～665 Hz 降至389～614 Hz，绝对带宽Abw1增加了225 Hz，相对带宽Rbw1从21.1%提升至44.9%。

图11 锥角变化对单胞A2 能带结构的影响Fig.11 The effect of cone angle variation on the band structure of unit cell A2

2.2.3 三叶飞镖单胞锥角对能带结构影响

单胞A3 能带结构随锥角α的变化如图12 所示，随着锥角的增加，单模传输区域上界频率fT2从258 Hz上升至309 Hz，绝对带宽Abw2增加了51 Hz，第一带隙绝对带宽Abw1与相对带宽Rbw1先增大后减小，当锥角α为28°时绝对带宽和相对带宽达到最大值，绝对带宽Abw1增加了78 Hz，相对带宽Rbw1从52.11%提升至65.22%。

图12 锥角变化对单胞A3 能带结构的影响Fig.12 The effect of cone angle variation on the band structure of unit cell A3

2.3 掺杂材料参数对能带结构影响分析

文献[21–22]已将材料参数对轴对称双锥单胞能带影响做了系统分析，发现软质填充材料杨氏模量对能带结构影响较大。对于材料对称分布的单胞，改变部分软质基体杨氏模量也会影响单胞的轴对称性，所以需要探究材料参数变化对能带的影响。单胞掺杂材料引入部位如图13所示，单独改变掺杂材料杨氏模量，观察能带的变化规律。

图13 三叶飞镖型非轴对称单胞A3 掺杂填充示意图Fig.13 Schematic diagram of A3 doping and filling of three leaf dart type non axisymmetric single cell

在引入掺杂材料的单胞A3 中，红色掺杂区域与其余软质材料填充区域杨氏模量差异越大，轴对称性越差。材料密度与其他参数保持不变，掺杂材料杨氏模量对能带结构的影响如图14所示。

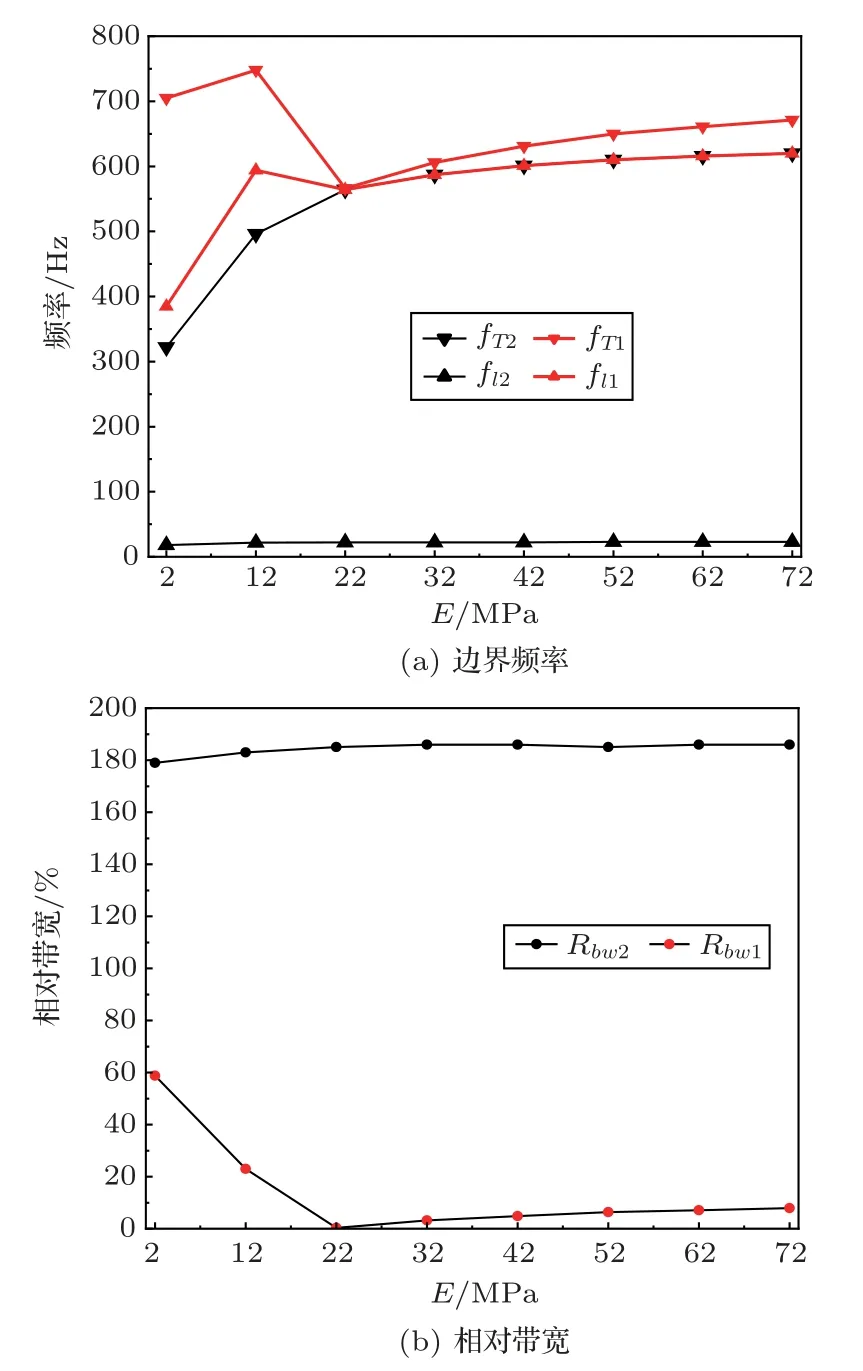
图14 掺杂材料参数对单胞A3 能带结构的影响Fig.14 Influence of doping material parameters on band structure of unit cell A3

随着杨氏模量的增加，单模传输区域上界频率fT2从322 Hz 上升至620 Hz，绝对带宽Abw2增加了293 Hz。扩大的单模区域上边界不断挤压禁带的活动空间，第一带隙相对带宽Rbw1逐渐减小。当E=22 MPa 时，位于低频段的能带解耦，单模上边界与第一带隙下边界重合，出现了一条绝对带宽为2 Hz 的禁带。由于单模区域上边界上升较快，受挤压的第一带隙宽度持续缓慢增长。E=72 MPa时第一带隙绝对带宽Abw1=51 Hz，相对带宽Rbw1=7.9%。相比母胞，在E=72 MPa 时单胞A3的单模相对带宽Rbw2提升了8%，单模绝对带宽Abw2提升了355 Hz。在实际单胞填充材料时，可选取适当模量的掺杂材料来提升单模区域宽度。

2.4 非轴对称对品质因数影响分析

改变对称程度影响单胞能带结构的同时，品质因数也会随之变化。轴对称对称程度对五模材料品质因数的影响如图15 所示。同种单胞随着硬质节点圆半径r或锥角α的增大，轴对称性逐渐降低，品质因数呈递减的趋势。在不同单胞间，随着飞镖型结构叶数的增多，轴对称性逐渐降低，品质因数逐级减小。值得注意的是，通过提升掺杂材料杨氏模量的手段可以显著改善单胞的品质因数，如图15(b)所示，当掺杂材料杨氏模量E=72 MPa 时，单胞A3与含掺杂材料的母胞的品质因数相当，大小约为2857，与没有引入掺杂的结构相比，单胞A3 品质因数提升了66.5%。在对二维五模材料进行非轴对称设计时，可以适当掺杂较高弹性模量的软质材料，以补足因不对称处理损失的品质因数。