一类捕食者－食饵模型的全局拓扑结构分析

张婷婷

（山西应用科技学院 信息工程学院，山西 太原 030062）

二十世纪以来，捕食者－食饵体系凭借其丰富多样的相互作用脱颖而出，迅速取得应用数学家的青睐，各种各样的捕食者－食饵模型得以发展并频繁出现在人们的视野之中.比率依赖的捕食者－食饵模型最早被提出并研究于20世纪80年代末，此后Gutierez［1］发展了比率依赖理论的生理基础，并用模型做出解释.在此基础上，RUAN等［2］对具有比率依赖功能反应函数的捕食者－食饵系统动力学行为进行了分析，并对其所有可能的分支进行了讨论.然而考虑到现实因素，由于自然资源的限制，捕食者彼此之间也会产生竞争，因此考虑捕食者密度依赖和猎物密度依赖的捕食者－食饵系统［3］更符合实际.

许多学者已经在这方面做出了贡献，JIANG等［4］考虑具有密度依赖性死亡率和比率依赖性功能反应函数的捕食者－食饵模型：

其中，x（t）和y（t）分别表示t时刻猎物和捕食者的种群密度.系统（1）各参数均为正，c表示猎物的内禀增长率，b表示猎物种群之间的相互干扰，d表示捕食者的死亡率，r表示捕食者密度依赖性死亡率.捕食者根据比率依赖的功能反应进行捕食，其中s表示捕获率，f表示能量转化率，m表示半饱和常数.文献［4］明确描述了系统（1）在原点周围的局部定性行为，基于原点周围的动力学和其他平衡点，对模型进行了有限平面全局定性分析.系统存在余维二的BT分支且经历了各种分岔现象，并用数值模拟说明理论结果.

然而研究平面系统轨线在全平面上的分布，除了解有限平面上的奇点性态和极限环的情况外，轨线在无限远处的性态也至关重要，而这关键取决于无穷远奇点的性态.目前在这些方面已经有了一些研究工作［5－7］.在文献［4］基础上，考虑无穷远处轨线性态，引入Poincaré变换探讨无穷远奇点的相关性态.将有限奇点与无穷远奇点结合研究系统的轨线在全平面上的分布情况，以Poincaré圆盘上做全局结构图的方法进行系统轨线的全局结构分析.

本文首先阐述了系统平衡点的存在性及其局部性态；其次分析了系统无穷远奇点，对系统轨线分布做全局分析；最后进行了总结讨论.

1 平衡点的存在性及局部性态

由文献［4］可知，系统（1）可变为

系统（2）始终存在1个灭绝平衡点（0，0）和1个边界平衡点（1，0），且在不同条件下，系统（2）可能存在0个，1个或2个正平衡点.当系统（2）存在唯一1个正平衡点E＊（x＊，y＊）时，E＊可能是局部渐近稳定的或是1个鞍结点，当系统（2）存在2个正平衡点E1（x1，y1）和E2（x2，y2）时，E1是1个鞍点，E2可能是局部渐近稳定的.

2 考虑无穷远奇点的全局性态

令z＝0，求解方程组

显然C（0，0）是奇点，且容易判定它是一不稳定结点.根据所确定的无穷远奇点个数及其类型，得到Poincaré圆盘如图1所示.

图1 系统（2）无穷远奇点邻域内轨线分布图

2.1 无正平衡点时全局结构分析

首先考虑系统（2）不存在正平衡点时的全局性态，在这种情况下灭绝平衡点（0，0）和边界平衡点（1，0）分别是吸引子（甚至是全局吸引子）的情形.

情况1（1，0）为鞍点，原点（0，0）处拓扑结构由椭圆扇形和抛物扇形组成，系统（2）有无数条轨线沿θ＝θ1离开原点，无数条轨线沿θ＝θ2进入原点，不存在极限环，（0，0）是全局吸引子，此时系统（2）全局结构图如图2（a）所示.

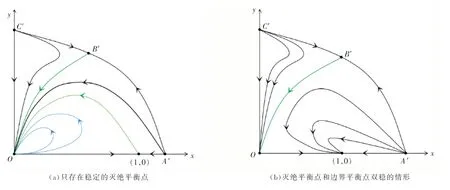
图2 系统（2）无正平衡点时全局结构图

情况2（1，0）为稳定结点，原点（0，0）处拓扑结构由抛物扇形和双曲扇形组成，系统（2）有一条线沿θ＝θ1离开原点，一条轨线沿θ＝θ3进入原点，无数条轨线沿θ＝θ2进入原点，不存在极限环，（0，0）和（1，0）是吸引子，此时系统（2）全局结构图如图2（b）所示.

情况3（1，0）为稳定结点，原点（0，0）处拓扑结构由双曲扇形组成，系统（2）有一条轨线沿θ＝θ1离开原点，一条轨线沿θ＝θ2进入原点，不存在极限环，（1，0）是全局吸引子，此时系统（2）全局结构图如图2（c）所示.

2.2 唯一正平衡点时全局结构分析

系统（2）存在唯一正平衡点时，边界平衡点（1，0）为鞍点，原点（0，0）或正平衡点E＊（x＊，y＊）分别是吸引子（甚至是全局吸引子）的情形.

情况4 原点（0，0）处拓扑结构由抛物扇形和双曲扇形组成，系统（2）有一条轨线沿θ＝θ1离开原点，一条轨线沿θ＝θ3进入原点，无数条轨线沿θ＝θ2进入原点，系统（2）的（0，0）和（x＊，y＊）是吸引子，当不存在极限环时，系统（2）全局结构图如图3（a）所示.

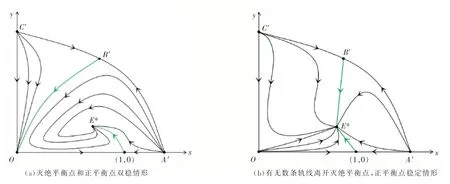
图3 系统（2）存在唯一正平衡点时全局结构图

情况5 原点（0，0）处拓扑结构由抛物扇形和双曲扇形组成，系统（2）有无数条轨线沿θ＝θ1离开原点，一条轨线沿θ＝θ2进入原点，有一条轨线沿θ＝θ3离开原点，不存在极限环，E＊是局部渐近稳定的，且是全局吸引子，此时系统（2）全局结构图如图3（b）所示.

情况6 原点（0，0）处拓扑结构由双曲扇形组成，系统（2）有一条轨线沿θ＝θ1离开原点，一条轨线沿θ＝θ2进入原点，不存在极限环，E＊是局部渐近稳定的，且是全局吸引子，此时系统（2）全局结构图如图3（c）所示.

情况7 原点（0，0）处拓扑结构由双曲扇形和抛物扇形组成，系统（2）有一条轨线沿θ＝θ1离开原点，无数条轨线沿θ＝θ2进入原点，E＊是局部渐近稳定的，且（0，0）和E＊是吸引子.当极限环不存在时，系统（2）全局结构图如图4（a）所示.

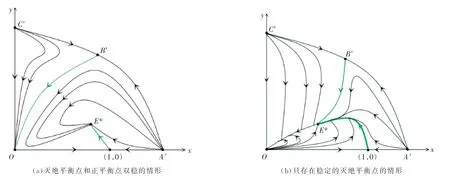
图4 系统（2）存在唯一正平衡点时全局结构图

情况8 原点（0，0）处拓扑结构由椭圆扇形和抛物扇形组成，系统（2）有一条轨线沿θ＝θ1离开原点，无数条轨线沿θ＝θ2进入原点，E＊是一个鞍结点，不存在极限环，（0，0）是全局吸引子，此时系统（2）全局结构图如图4（b）所示.

2.3 两个正平衡点时全局结构分析

系统（2）存在两个正平衡点时，边界平衡点（1，0）和E1是鞍点，（0，0）和另一个正平衡点E2是吸引子.

情况9 原点（0，0）处拓扑结构由椭圆扇形和抛物扇形组成，系统（2）有无数条轨线沿θ＝θ1离开原点，无数条轨线沿θ＝θ2进入原点，E2局部渐近稳定，（0，0）和E2是吸引子，当极限环不存在时，系统（2）全局结构图如图5所示.

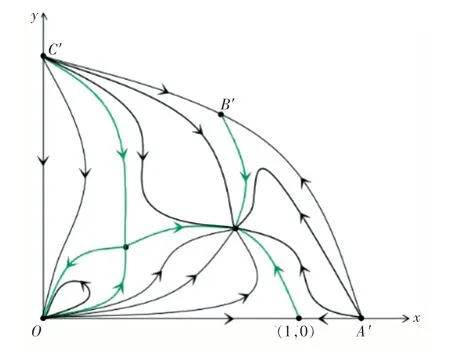
图5 系统（2）存在两个正平衡点时全局结构图

3 讨论

利用微分方程定性理论，对一类具有密度依赖死亡率和比率依赖功能反应函数的捕食者－食饵模型进行了系统轨线的全局结构分析.当系统（2）不存在正平衡点时，由于边界平衡点（1，0）是吸引子，故疾病灭绝；当系统（2）存在唯一正平衡点时，正平衡点E＊（x＊，y＊）是吸引子，故疾病流行；系统（2）存在两个正平衡点时，其中E1是鞍点，另一个正平衡点E2是吸引子，故疾病流行.