图书馆自助借还机数量优化研究

董秀，李艳梅，张杰，董书一

（1.阜阳师范大学 图书馆，安徽 阜阳 236037；2.阜阳师范大学 数学与统计学院，安徽 阜阳 236037；3.蚌埠三十一中，安徽 蚌埠 233000）

近年来，随着知识在经济建设中作用的不断增强，图书馆，特别是高校图书馆在人才培养过程中所起的重要作用越来越凸显.图书馆一方面需要加强图书资源的软硬件建设，另一方面还要提升其服务质量和服务效率，从而提高读者满意度.为此，在信息化和智能化高速发展的大背景下，许多图书馆都购置了一些自助借还机.我校图书馆就购置了6台用于读者借还图书.为了减少读者排队等待时间，提高服务效率与管理水平，本文拟用排队论，特别是异步休假排队对自助借还机进行优化配置.

1 基于休假排队的借还机服务模型

1.1 休假排队简介

图书馆流通部的主要任务是保障读者能借到所需图书以及图书的正常流通，并使读者方便快捷地获得服务.显然，机器配置过多会出现机器空闲，从而造成资源和能源的浪费；而配置过少，会导致系统中读者队列过长、等待时间过长，降低读者满意度.为此，本文拟主要以平均等待时间和平均队长为性能指标，对借还机进行优化配置.

假设需要借还书的读者到达服务系统的到达率服从参数为λ的泊松分布；到达服务系统后按先来先服务（first come，first served，FCFS）规则排队，然后由一个无形的调度器按FCFS策略对其进行调度.假设每台机器的服务率相同，且服从参数为μ的负指数分布，由此可用M／M／c排队系统对借还机服务进行建模.

但在某些时候，如某些机器出现故障、网络出现问题需要维护和保养，系统就不能提供服务.显然，不能应用经典排队模型解决该问题.因此，应采用更加符合此情形的随机服务理论——具有休假的排队解决该问题.

休假排队作为随机运筹中一个具有独特特征的研究方向，它允许服务台在空闲期可休假.LEVY等［1］首先研究了M／G／1型休假模型以有效利用排队系统闲期.LEVY等［2］使用经典生灭过程讨论指数休假时间的M／M／c排队系统，但在求解过程中遇到很大困难.VINOD［3］首先采用拟生灭（quasi birthdeath，QBD）过程研究M／M／c休假排队.田乃硕等［4－5］使用QBD 过程和矩阵几何解方法研究了具有各种休假策略如同步休假、异步休假以及部分服务台异步休假的M／M／c排队，建立多服务台休假排队理论的架构.由于休假排队系统更能客观地反映服务可能中断的事实，同时还为系统的优化设计和过程控制提供灵活性，受到广泛关注，并在云计算［6－7］、交通［8］、社会管理［9］、电子信息［10］等领域得到了广泛应用.本文拟基于部分服务台异步休假的M／M／c排队系统建立借还机服务模型，从而对其配置进行优化.

1.2 基于部分借还机多重休假的M／M／c服务模型建立

在1.1节所述参数为λ和μ的经典M／M／c排队的基础上引入部分借还机异步多重休假策略.具体部分借还机异步休假服务模型描述如下.

（i）d表示允许异步休假的借还机数，即1≤d≤c；

（ii）某台借还机完成某次服务时，若没有读者等待服务，可能发生两种情况：若正在休假的借还机数m＜d，则该借还机开始休假；若m＝d，则该借还机不能休假而进入空闲状态，即借还机有忙、空闲和休假3种状态.否则，有读者等待时，则继续为下一个读者服务；

（iii）某台借还机结束休假时，若有读者在等待服务，则它结束休假，开始借还服务，即由休假状态转为工作状态；否则，开始另一次独立同分布休假；

（iv）借还机的休假时间V 服从参数为θ的负指数分布；

（iiv）随机变量λ、μ和θ彼此之间相互独立.

由上面的描述可知，在任意时刻t处于休假状态的借还机数不超过d，至少有c－d台借还机供读者使用.假设系统达到平稳状态时有k个读者（包括正在接受服务的读者和等待的读者），当0≤k≤c－d时，处于休假状态的借还机达到最大值d，k台处于工作状态，其余的处于空闲状态；当c－d＜k≤c时，系统中至少有c－k台正在休假且没有空闲的借还机；当k＞c时，某时刻可能有j（0≤j≤d）台借还机均处于休假状态，其余处于工作状态.

下面利用QBD 过程，求解系统处于稳态下的队长和等待时间.令Lv（t）表示t时刻系统内读者数，J（t）表示t时刻正在休假的借还机台数，则｛（Lv（t），J（t））｝构成一个二维Markov过程和一个QBD 过程，其状态空间Ω 如下：

当有读者到达系统、服务完成和借还机休假结束时，状态发生会改变.当c＝6、d＝2时按层次将该过程的状态排序的状态转移机制如图1所示.图1中最下层表示没有借还机休假，中间层表示有1台借还机休假，最上层表示有2台借还机休假.例如，状态（7，2）表示系统中当前有7位读者，且2台借还机处于休假状态，其余4台处于服务状态.当有读者到达时它以λ速率转移至状态（8，2）；系统以4μ的服务速率运行，它以4μ速率转移至状态（6，2）；若有1台借还机休假结束，它以2θ速率转移至状态（6，1）.

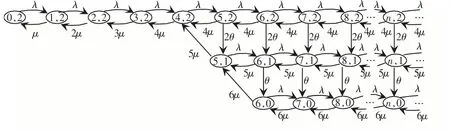
图1 允许2台借还机异步多重休假M／M／6排队的状态转移图

称状态集｛（k，m），…，（k，n）｝，k≥0为水平k，如水平7为｛（7，0），（7，1），（7，2）｝.将状态按字典序排列，且同一水平k内的状态自j＝d开始按递减顺序排列.图1中（0，2）至（7，0）行、（0，2）至（8，0）列的无穷小生成元矩阵为

图1的无穷小生成元矩阵可将其写成如下分块三角阵.

A、B和C均为d＋1阶方阵，且C＝λI，

1.3 基于率阵的模型求解

定理1［11］当ρ＝＜1时，矩阵方程

的最小非负解

称为率阵，其中rkk（0≤k≤d）是方程（3）

在（0，1）内的根，且非对角线元素满足

当ρ＜1时，令（Lv，J）表示过程（Lv（t），J（t））的稳态极限，并记为

定理2［11］ρ＜1时（Lv，J）的分布Pk可表示为

其中α0，α1，…，αc－d，αc－d＋1，…，αc是方程组

的正解，其中pk＝（pkd，pkd－1，…，pkc－k），c－d＋1≤k≤c，

K为常数因子，

其中e为元素全为1的列向量.

2 仿真实验

2.1 参数设置与性能指标

假设有6台借还机，最多允许2台借还机进入休假状态，读者到达平均时间间隔为5min，处理1次借还书平均需要30s，即c＝6，d＝2，λ＝0.2，μ＝2，θ＝0.1.考虑2个借还机休假的M／M／6排队的借还系统.此时，

由定理1得其率阵R：

和10阶方阵B（R）.由定理2，将其代入方程组

解得其根即稳态下（Lv，J）联合分布的数值解为

2.2 λ对系统性能的影响

取λ∈｛0.5n｜1≤n≤10，n∈｝，其他参数不变，得到相关性能指标变化情况，如图2.可以看出，随着读者到达率的增加系统中平均读者数先增后减，而处于休假状态的借还机数和读者平均等待时间不断减小.其原因是当读者到达率较低时，如介于0.5～3.0时，系统中处于休假状态的借还机数达到最大值2（Lv的值采取四舍五入取整），即参与服务的借还机达到最小，所以此时Ls不断增加；当到达率达到一定数值时，处于休假的借还机因休假结束而参与工作从而使Ls、Lv和Ts均呈递减趋势.

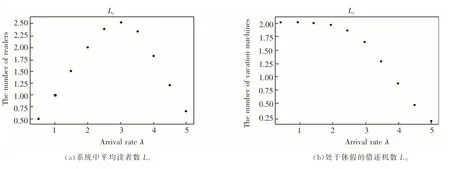
图2 不同读者到达率对系统性能的影响

2.3 d对系统性能的影响

在2.2节基础上，取d＝0，1，2，3，其他参数不变，得实验结果如图3.可看出，不管d取何值，Ls都呈先增后减趋势，Ts基本呈减小趋势.读者到达率λ＝2.5为其临界点，也就是说，当λ＜2.5时，不同的允许休假借还机台数对系统性能指标影响较小；当λ＞2.5时，无论是系统中读者数还是等待时间等性能指标都有较大影响，随着d的增加，两个重要指标都显著减少，系统性能得到提升.其原因是λ＜2.5时，到达率较低不足以使休假的借还机转为工作状态，导致随d的增加，其性能略显降低.相较于不允许休假，借还机在空闲期休假时得以维护和保养，当到达率较高时借还机不会出现故障从而性能得以提升，但如果休假台数过高将导致性能降低.从另一个侧面也说明借还机进行休假的必要性.因此，借还机休假不但可以在一定程度上节约资源和能源、延长机器使用寿命，而且可以提升性能，进而提升读者满意度.

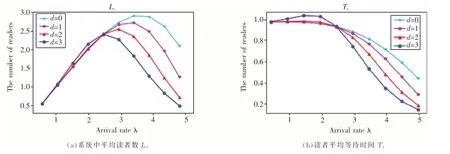
图3 不同允许休假借还机台数对系统性能的影响

3 小结

降低图书馆流通借还书系统排队时间已成为提高读者满意度的有效途径之一.为此，本研究提出部分借还机异步休假的M／M／c排队模型对借还机的配置进行优化，充分发挥其服务能力，以减少等待时间和队长.仿真结果表明借还机休假可以提高系统性能，且就6台借还机而言，允许休假借还机台数为2时，其性能达到最佳.因此，本文提出的模型不仅具较强的科学性和理论性，而且能够为相关高校图书馆借还机配置优化提供参考和借鉴.