2023年湖南省高考物理压轴题赏析、溯源与拓展
2023-11-20姚华鑫
姚华鑫
(北京师范大学未来教育学院)
2023年湖南省高考物理试题以物理学科核心素养为导向,知识点覆盖面较广,突出时代性和实践性,同时兼顾基础性与选拔性.试题立足物理学科知识网络体系,注重数学知识的运用,加强了综合性,体现了高考试题服务选才的功能.其中的压轴题是一道综合物理规律与数学知识的题目.该题目要求学生深入掌握模型的运动规律,综合性和应用性较强,考查了学生的推理论证能力和数学方程化表达能力.
1 原题呈现
原题如图1所示,质量为M的匀质凹槽放在光滑水平地面上,凹槽内有一个半椭圆形的光滑轨道,椭圆的半长轴和半短轴分别为a和b,长轴水平,短轴竖直.质量为m的小球,初始时刻从椭圆轨道长轴的右端点由静止开始下滑.以初始时刻椭圆中心的位置为坐标原点,在竖直平面内建立固定于地面的直角坐标系xOy,椭圆长轴位于x轴上.整个过程凹槽不翻转,重力加速度为g.

图1
(1)小球第一次运动到轨道最低点时,求凹槽的速度大小以及凹槽相对于初始时刻运动的距离;
(2)在平面直角坐标系xOy中,求出小球运动的轨迹方程;
2 试题分析
2.1 试题情境
本题以一道动态的椭圆摆模型为情境,巧妙设置以数学知识为载体的物理试题,涉及动量守恒定律和机械能守恒定律,辅以运动轨迹的数学方程表达,属于综合性和应用性较强的题目,难度较大.
2.2 必备知识
该题通过对小球和凹槽运动过程中的状态量的计算,考查动量守恒定律的应用、机械能守恒定律适用条件的判断与运用、数学曲线方程表达、速度的分解与合成以及变换参考系分析问题等知识.
2.3 能力素养
本题考查的关键能力主要有理解能力、推理论证能力和模型建构能力,凸显了物理学科核心素养.本题要求学生具备运用数学知识解决物理问题的能力,实现物理规律数学化表达的能力.在理解能力方面,该题要求学生能从基本的球摆模型中挖掘有效信息,认识到小球在不同形状的轨道中运动所满足的共同的物理规律与定律.在推理论证能力和模型建构能力方面,求解小球的轨迹方程要求学生具备运用物理知识建立相应的数学模型的能力,用数学化的表达式表现其中所蕴含的物理规律;第(3)问要求学生能充分挖掘题设轨迹的特点,并运用几何关系分解小球速度,达到解决问题的目的.
2.4 解题过程
(1)水平地面光滑,小球运动到最低点的过程中,小球和凹槽水平方向不受任何外力,小球和凹槽组成的系统水平方向动量守恒.
设小球运动到最低点时的速度为v1,凹槽的速度为v2,于是可得mv1=Mv2.
由于接触面均光滑,可知系统机械能守恒,可得
解得
在水平方向采用微元法,由水平方向动量守恒得
对小球从释放到第一次运动到轨道最低点过程求和,可得mx1=Mx2,又x1+x2=a.
联立上述各式解得
(2)解法1以地面为参考系,由于水平方向动量守恒,系统的质心在水平方向上不动,设小球在某时刻的坐标为(x,y),凹槽水平位移为z,可得Mz=m(a-x),解得.根据数学知识可得此时小球运动轨迹的椭圆方程为.
该解法是在已知小球运动轨迹是椭圆的基础上得出的.后面我们将分析此模型下小球运动轨迹是椭圆具有普遍性.
解法2设在地面S参考系中小球的横坐标为x,小球和凹槽的水平位移分别为x1和x2;设在凹槽S′参考系中小球的横坐标为x′,如图2所示.
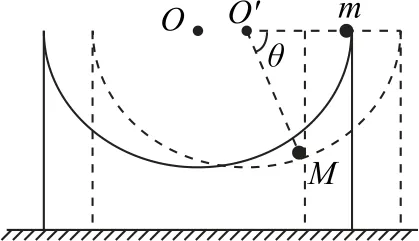
图2
根据小球在两个参考系中的相对关系,由运动情况不难得出在S′系中小球的坐标满足
在S系中有x=x′+x2,x+x1=a,由水平方向动量守恒有mv1x=Mv2,即有mx1=Mx2,又y=y′.
联立以上各式解得
解法2是在变换参考系的情况下,根据二者的位移关系解得轨迹方程.该种解法比较符合学生的认知水平和知识储备,是教学中处理该类问题的常见做法.
(3)解法1将代入式②整理可得
此时小球的运动轨迹是以(a-b)为圆心,b为半径的圆.
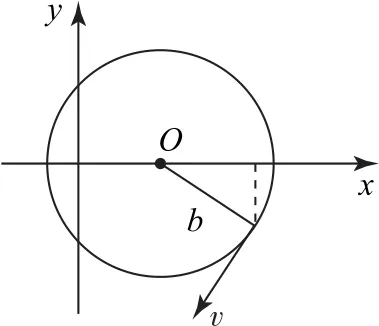
图3
根据机械能守恒可得
解法2对式①进行隐函数求导可得
整理可得
3 题目溯源
如图4所示,半圆形光滑槽质量为M,半径为R,置于光滑水平地面上.一质量为m的小球可在槽内自由滑动.开始时小球由A处静止释放.求:

图4
(1)m滑到最低点时,m、M对地的速度大小;
(2)在最低点时m对槽的压力;
(3)m对地的运动轨迹在最低点的曲率半径;
(4)m对地的轨迹方程.

(1)系统水平方向动量守恒且全过程系统的机械能守恒,可得在最低点有
(2)当m运动到最低点时,槽没有加速度,可选作惯性参考系,此时m相对于M的速度为v1+v2,m相对于M的运动半径为R,根据牛顿第二定律可得
(3)以地面为参考系,小球的运动轨迹不是一个圆,设小球经过最低点时对应的曲率半径为ρ,根据牛顿第二定律得
(4)以地面为参考系,建立向右为x正方向、向下为y轴正方向的平面直角坐标系,如图5所示.设小球在某时刻的坐标为(x,y),光滑槽的水平位移为z,由于水平方向动量守恒,系统的质心在水平方向的位置不变,可得Mz=m(R-x),解得.由图可知任意时刻小球的坐标为

图5
联立上述各式可得可见小球的轨迹为椭圆的一部分,椭圆的中心为,半长轴为R,半短轴为.
小结通过上述解答过程,我们发现在一般情况下,无论凹槽的轨道是圆轨道还是椭圆轨道,小球相对于地面参考系的轨迹都是椭圆方程的一部分.不同点在于,凹槽是椭圆轨道时,我们可以调整小球与凹槽的质量比,使得小球的运动轨迹为圆弧.
4 拓展思考
4.1 揭开影响小球轨迹方程的面纱
如果凹槽的轨道形状不再是圆或者椭圆,那么小球相对于地面参考系的运动轨迹还是椭圆或者圆轨道的一部分吗? 接下来我们将推导凹槽轨道是抛物线时小球相对于地面参考系的轨迹方程.
我们以地面参考系为S系,以凹槽参考系为S′系.设小球在S系中的横坐标为x,小球和凹槽的水平位移分别为x1、x2;在S′系中小球的横坐标为x′,设凹槽曲线的抛物线方程为y=-ax2+a,如图6 所示,根据相对运动情况有如下关系.
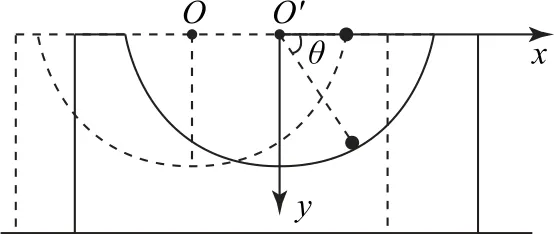
图6
在S′系中小球的坐标满足y′=-ax′2+a,在S系中有x=x′+x2,x+x1=a.由水平方向动量守恒可知mv1x=Mv2,即mx1=Mx2.又y′=y.
联立上述各式解得
由数学知识易知上述小球的轨迹为抛物线方程,开口朝上,轨迹的最低点向右平移个单位.这时我们得出结论,小球相对于地面参考系的运动轨迹取决于凹槽的形状.
4.2 揭开小球速度最大值出现位置的面纱
为研究方便,我们选取凹槽形状是圆的情况来探讨小球最大速度出现的位置.当二者的质量之比满足什么条件时,小球最大速度出现在最低点呢?
小球在S′系中做圆周运动,设图中小球在该系中的速度为,二者在S系中的速度分别为v1、v2.此时小球和凹槽圆心的连线与水平方向所成夹角为θ,如图7所示.
水平方向有v1x=-v2.
竖直方向有v1y=.
在S系中,根据动量守恒定律和机械能守恒定律可得mv1x=Mv2,即
联立上述各式可得
接下来,我们探讨这个小球最大速度出现在最低点时k所满足的条件.
令x=sinθ∈(0,1),整理可得
令u=x2∈(0,1),这是一个关于u的二次方程.对称轴,故上式二次方程的最小值在u=1时取到,如要恒成立,则需最小值都要大于零,即有
整理可得2k2+2k-1≤0,解得,故当时,小球的速度最大值出现在最低点;当时,小球的速度最大值出现在最低点两侧.
5 教学启示
一道高考题的设计是命题专家深思熟虑后完成的,经典模型不按套路出牌将会成为新高考试题的亮点.这道高考压轴题实质上是一道经典模型题目的改编题,只是将圆轨道改成了椭圆轨道.这就启示我们在未来物理教学中,要对教材和课后习题中的典型题目进行深入挖掘,开展“一题多解、一题多变、多题归一”的变式训练,让学生透彻理解题目中的物理规律本质.当然,我们也可以通过小组讨论的形式,让学生自主改编试题并进行自我解答,从而引导学生在讨论分享中形成多样化的问题意识,碰撞出思维的火花.
(完)

