一种改进的短签名云数据审计方案
2023-11-17崔圆佑王绪安苏昀暄
崔圆佑,王绪安,郎 讯,涂 正,苏昀暄
(1.武警工程大学 密码工程学院,陕西 西安 710000;2.武警安徽总队,安徽 合肥 230000;3.武警贵州总队,贵州 贵阳 550000)
1 引 言
近年来信息时代迎来了云计算、云存储和物联网等新科技。物联网将所有的信息实体连接到互联网上,包括计算机、可穿戴智能设备、传感器等。云计算需要强大的存储能力,一方面是为用户提供强大的计算能力[1],另一方面用户为了使用方便也更愿意将数据存储在云端。云存储与云计算紧密相连,同时前者是后者提供的最主要的服务之一。虽然云存储具有数据管理高效、存储空间扩展便利、成本较低和使用方便等优点,但是云存储器也因为其开放性和存储数据的高价值,使之成为恶意攻击的重点。同时云服务提供商也可能出于节约存储空间和窃取用户秘密的目的,破坏、删除或者修改用户存储的数据。因此用户必须审核存储在云端的数据,保证云端数据的完整性不被破坏。
数据完整性审计[2-3]是指用户在上传原始数据后,在不直接访问全部原始数据的情况下,通过某项协议达到对云端数据完整性验证的目的。数据完整性审计的思想是首先由云存储服务提供商通过计算用户上传的原始数据产生一个能够证明数据完整性的签名或者证据,然后返回给用户。验证前用户首先对原始数据进行处理和计算,得出一些特征信息并存储在本地,然后验证时则根据申请验证前存储的一些信息,来对要求云端返回证据的正确性进行验证,从而确保数据完整性不被破坏。依据是能否修复出错数据文件,经典地分为数据持有性证明机制(Provable Data Possession,PDP)和数据可恢复性机制(Proofs Of Retrievability,POR)。2001年由BONEH等[4]提出了BLS签名机制,这是一种对数据完整性验证的次数没有限制且能够支持公开验证的短消息签名机制。在这个PDP机制中,利用BLS签名替代Ateniese方案中的RSA签名。2004年,为了解决审计次数受限的问题,DESWARTE等[2]利用具有同态特性RSA签名算法(am)r=amr=(ar)mmodN,提出了基于RSA签名的PDP验证机制。但是引入RSA算法依然无法解决计算开销过大的难题。因此,2006年,FILHO等[5]在此基础上引入了欧拉函数φ(n)来降低计算量,提高传输速度。2007年与2011年,ATENIESE等[6-7]对此进行改进。此方案通过引入数据文件分块技术和同态认证标签成功降低了计算规模,并把多个数据块的值通过计算聚合为一个值。而且采用抽样的策略,通过概率性证据而不是绝对性证据对云端数据进行数据完整性检测,进一步降低了计算的开销。2011年,WANG等[8]提出了一种基于BLS同态签名和RS纠错码的方案,用以实现可证明的数据持有性证明PDP。该验证方案使用默克尔哈希树(Merkle Hash Tree,MHT)和 BLS保证存储的数据块的正确性,支持数据的公共验证和动态更新。此外,2008年,CURTMOLA等[9]提出了新的数据持有性验证机制(MR-PDP),用以实现支持多副本的数据完整性证明。在提高数据安全性的同时,降低了对多个副本逐一进行验证的开销之和。2016年,李勇等[10]利用多分支路径树(Large Branching Tree,LBT)来存储处理数据块,从而构造了新的数据完整性验证方式(LBT-PDP),用以取代之前的跳表。2019年,ZHU等[11]设计了一种基于ZSS短签名的,可用于审计云物联网数据的方案,从而降低开销。2020年,毛向杰等[12]设计了一种云数据完整性混合验证方案。为实现高效验证,该方案中静态验证使用基于BLS签名的验证方式,动态验证使用基于多分支路径的验证方式。2020年,杨小东等[13]提出了一种基于秘密共享技术和多分支路径树的多用户多副本云端数据公开审计方案。为了满足用户安全撤销的需求,该方案引入了重签名算法。此外,2020年,咸鹤群等[14]提出了一种无需第三方审计者(Third Party Auditor,TPA)在线参与的云存储数据删重方案,确保在进行流行度调查时不泄露明文信息。2022年,杨海滨等[15]设计了一种无双线性对的云审计方案,通过Schnorr算法和区块链技术只生成被审计数据的标签,从而降低开销。
然而文献[11]的方案中存在一些瑕疵,还不够严谨。主要是在证据生成过程中,生成的部分证据无法进行运算,不满足加法循环群的运算法则。文中在原数据验证协议的基础上进行了一些调整,弥补了原方案中的不足。通过分析该方案的安全性,证明了文中对ZHU等原方案的优化和改进是有效的。
2 系统模型
ZHU等方案的系统模型如图1所示,共有3个实体组成: 用户、云服务提供商(Cloud Service Provider,CSP)和第三方审计者(Third Party Auditor,TPA),也就是User/Client、CSP和TPA。具体的应用场景包括物联网、医疗系统、电力系统或者其他工业系统等。医疗系统中可以传输相关医疗数据,电力系统中可以传输相关用户信息,物联网中可以依托传感器等收集和传递相关信息。
(1) 用户(User/Client):主要包括对数据有存储需求的用户和对数据进行收集的设备。以物联网为例,网络控制中心将传感器收集到的用户数据存储在CSP提供的云存储服务器上,用户可以与云存储服务器建立通信。此外,TPA受用户委托审计云端存储数据的完整性。
(2) 云服务提供商:提供的业务包括数据的存储和计算。

图1 基于物联网的云审计系统模型
(3) 第三方审计者:具有专业能力的、独立可信第三方。它不知道所存储的具体的数据。在获得用户审计授权后,它向存储用户数据的云服务器发起验证申请。
工作流程如下:
① KeyGen(k)→(pk,sk):输入安全参数k,输出用户的的公钥pk和私钥sk。
② SigGen(sk,m)→σ:输入一个文件m和私钥sk,输出数据块的签名集σ。
③ GenProof(m,σ,chal)→pf:将一个文件m、一个签名集合σ和生成的挑战信息chal作为输入,输出由挑战信息chal指定的数据块的占有证明pf。
④ VerifyProof(chal,pf)→{TRUE,FALSE}:将一条挑战信息chal和一条完整性证明pf作为输入,输出结果为真(TRUE)或为假(FALSE)。
3 原方案
3.1 方案结构

具体结构如下:

(2) SigGen(sk,m)→σ:签名时,用户计算出对应的数据块的签名σ。文件m被分割为数据块{m1,m2,…,mn},mi是其中任意一个数据块,其对应的签名为σi。
令签名:
(1)
则文件m的签名为σ={σ1,σ2,…,σn}。用户将文件m和签名σ打包为{m,σ}发送给CSP,将签名σ发送给TPA,将本地保存的文件m删除。
首先TPA生成挑战信息,然后发送给CSP。TPA从集合{1,2,…,n}选择c个元素组成新的集合I={s1,s2,…,sc},其中1≤s1≤…≤sc≤n。对于任意i∈I,首先TPA生成一个伪随机数vi=φ(kO,i),然后发送一个挑战信息chal={(i,vi)}s1≤i≤sc给CSP。
(3) GenProof(m,σ,chal)→pf:在CSP收到TPA的挑战信息chal和受挑战的数据块的签名{σi}s1≤i≤sc后,计算:
(2)
(3)
(4)
最后,CSP将证据pf={R,μ,η}发送给TPA。
(4) VerifyProof(chal,Pf)→{TRUE,FALSE}:在这个阶段,TPA在收到证据pf后,对相应的签名{σi}s1≤i≤sc进行验证。通过对下面的等式进行验证,判断被第三方审计挑战的数据块是否被正确地持有:
e(η,P)·e(μ+R,P)=e(P,P) 。
(5)
3.2 存在的正确性问题
(1) 根据循环群的定义,若一个群G的每一个元都是G的某一个固定元a的乘方,则称G为循环群,记作G=(a)={am|m∈Z},此时称a为群G的一个生成元。 简单地理解,就是循环群内的运算,如加法或者乘法,是以生成元的整数幂次(整数倍)的运算。 假设G的代数运算用加号表示时,有G= (a)={am|m∈Z}。

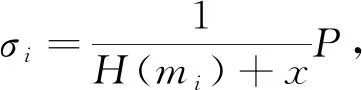
(2) 根据椭圆曲线运算特点,假定P点为(a1,b1),Q点为(a2,b2),P+Q为(a3,b3)。因此当在进行形如2P,3P,…,NP的计算时,这个不是单纯的2×P乘法这么简单,而是要进行如P+Q的运算,如2P=P+P,3P=P+2P等。
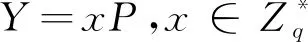
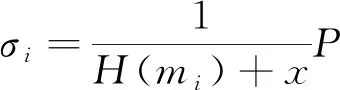
3.3 存在的安全性问题
(1) 根据ZSS短签名所基于双线性映射的双线性特征,e(k1P+k2P,P)=e(k1P,P)·e(k2P,P),可知要使TPA证据验证时等式e(η,P)·e(μ+R,P)=e(P,P)成立,只需要满足e(η+(μ+R),P)=e(P,P),即Y=xP。 而要使等式η+(μ+R)=P成立,显然是容易的,例如攻击者可以伪造证据pf′={R′,μ′,η′},令η′=3P,μ′=-P,R′=-P。
攻击者可以是恶意的CSP,通过伪造证据pf={R,μ,η},欺骗TPA进行完整性审计,实现篡改云存储服务器中的数据,甚至不需要存储任何数据,从而节约存储空间。 某未知攻击者也可以截获用户上传的数据后,将错误的数据上传给云服务器,而在TPA进行审计时,直接冒充CSP回复证据。
(2) 原方案无法抵御重放攻击。 假设某次审计生成的挑战为chal1,第2次审计生成的挑战为chal2,则CSP两次生成的证据分别为pf1={R1,μ1,η1}和pf2={R2,μ2,η2}。
TPA第1次发出挑战时,CSP生成的证据pf1能够通过等式e(η,P)·e(μ+R,P)=e(P,P)的验证。此时CSP保存第1次审计时的证据pf1。 在TPA第2次发出挑战时,恶意CSP可以将存储的数据直接删除或篡改的情况下,直接返回第1次的证据pf1同样能通过验证。 因为pf1已经证明是正确的,同时在e(η,P)·e(μ+R,P)=e(P,P)中,3个变量η,R,μ均为已知。所以恶意CSP可以利用pf1应对所有TPA的审计。
4 改进的方案
4.1 方案改进
文中针对原方案中暴露出的运算正确性问题提出了优化方案,主要是改进优化了证据pf中的η的生成算法。

(2) SigGen(sk,m)→σ:签名时,用户计算出对应的数据块的签名σ。 文件m被分割为数据块{m1,m2,…,mn},mi是其中任意一个数据块,其对应的签名为σi,与原方案的式(1)相同。
因此,文件m的签名为σ={σ1,σ2,…,σn}。 用户将文件m和签名σ打包为{m,σ}发送给CSP,将签名σ发送给TPA,将本地保存的文件m删除。
首先TPA生成挑战信息,然后发送给CSP。 TPA从集合{1,2,…,n}选择c个元素组成新的集合I={s1,s2,…,sc},其中1≤s1≤…≤sc≤n。 对于任意i∈I,首先TPA生成一个伪随机数vi=φ(kO,i),然后发送一个挑战信息chal={(i,vi)}s1≤i≤sc给CSP。
(3) GenProof(m,σ,chal)→pf:在CSP收到TPA的挑战信息chal和受挑战的数据块的签名{σi}s1≤i≤sc后计算:R、μ和η。 其中R和μ与原方案的式(2)和式(3)相同,η的计算公式为
(6)
最后,CSP只将证据pf*={μ,η}发送给TPA。
(4) VerifyProof(chal,Pf)→{TRUE,FALSE}:在这个阶段TPA在收到证据pf*={μ,η}后,通过之前发送给CSP的挑战信息chal={(i,vi)}s1≤i≤sc和公钥Y=xP,计算出:
(7)
通过对下面的等式进行验证,判断被可信第三方挑战的数据块是否被正确地持有:
e(μ+R*,η)=e(P,P)H(R*)+H(μ)。
(8)
4.2 正确性分析
定理1在优化改进的云审计方案中,假如TPA和CSP可以互相正确应答相关信息,且能完成完整性审计,则证明方案正确。
证明:根据改进的方案,在验证阶段,如果TPA与CSP互相传递的信息无误,那么CSP提供给TPA的证据pf={R,μ,η}也是正确的;如果TPA验证时能够通过下面的等式,则表明改进的方案是正确的,即
e(P,P)H(R)+H(μ)=
e(P,P)H(R*)+H(μ)。
4.3 安全性分析

证明:为了实现用户外包数据的完整性审计,用户首先计算外包数据的数据块标签,然后发送给TPA:
同时,TPA能够自行获取用户的公钥Y=xP。
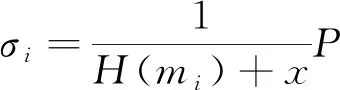
定理3TPA无法通过 CSP 提供的证据pf={μ,η},来恢复用户的数据。
证明:假设在随机预言机模型下,存在一个模拟器Γ能够在没有获得用户隐私数据的前提下生成正确的回复。假定TPA为敌手A1,此时A1通过构建模拟器Γ来模拟TPA的输入和输出,模拟器Γ拥有公钥pk和签名σ等公开的信息。
攻击者A1输入集合I={s1,s2,…,sc}和证据pf*={μ,η},输出结果TRUE或者FLASE。 构造的模拟器将执行以下操作:
(1) 模拟器Γ选择随机数i∈Zq且i∈{1,2,…,n}。
(2) 模拟器Γ从集合{1,2,…,n}中选择c个元素组成新的集合I={s1,s2,…,sc}。
(3) 模拟器Γ生成一个挑战信息chal={(i,vi)}s1≤i≤sc给CSP。
(4) 此时攻击者A1得到CSP返回给TPA的证据pf*={μ,η}。

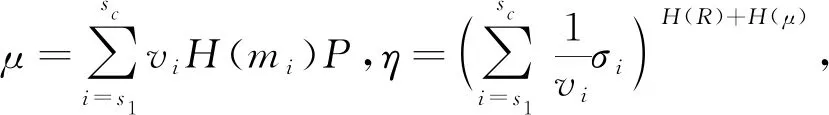
定理4不存在一个概率多项式时间(Probabilistic Polynomial-Time,PPT)的攻击者A能够使用算法P伪造出证明pf′,并通过完整性验证。
证明:假设存在一个攻击者A,可以伪造签名并骗过TPA审计。此时攻击者A生成相应的证据pf′={μ′,η′}能够使等式e(μ′+R*,η′)=e(P,P)H(R*)+H(μ′)成立。
定理5改进方案能够抵御前文给出的第1种攻击。
证明:改进的方案中TPA进行验证的等式为
e(μ+R*,η)=e(P,P)H(R*)+H(μ)。
通过在等号右侧进行H(R*)+H(μ)次幂运算,避免出现验证等式e(μ+R,η)=e(P,P)的情况。若等号右侧未进行H(R)+H(μ)次幂运算,则伪造证据仅需满足:
(9)
而通过在等号右侧进行H(R*)+H(μ)次幂运算,为使等式e(μ+R*,η)=e(P,P)H(R*)+H(μ)成立,即令e(μ+R*,η)=e(P,(H(R*)+H(μ))P),则需要满足:
(10)
此时P、μ+R和η均在椭圆曲线上,且μ、R和η均未知,寻找a,b,μ,R,η满足等式(9)是困难的,因此构造满足条件的证据pf*={μ,η}和R*是困难的,且R*在TPA上,无法伪造。定理5证毕。
定理6新方案能够抵御重放攻击。

4.4 性能分析
文中分析对比了新方案与原方案中的计算开销。为了更好地对比两者之间的性能差异,首先分别对两个方案中用户、CSP和TPA的计算开销进行分析,然后进行对比,得出变化量。计算符号含义如表1所示。

表1 计算符号含义
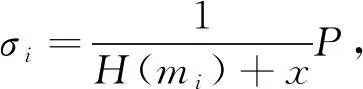
从表2可以看出,文中改进方案的标签的计算开销与原方案相同。 同时发现,一方面在新方案中CSP针对TPA的挑战,生成证据的计算开销有所增加,生成证据的时间变化量与审计的数据块量呈线性关系;另一方面,新方案中TPA进行完整性验证的计算开销的变化量,不随审计数据块数量的变化而变化。 最后新方案整体的计算开销变化不大,而且比原方案提供了更好的计算准确性。此外在通信开销上原方案CSP上传的证据为pf={R,μ,η},新方案为pf*={μ,η},节约了通信开销。

表2 计算开销对比
5 结束语
笔者发现ZHU等的方案虽然运算效率较高,但是在验证过程中存在计算方面的问题,这意味着该方案在实际运行中会存在诸多问题。针对存在的问题,文中在原方案的基础上进行优化,提出改进方案,对安全性进行验证,同时改进的方案较大地压缩了ZHU方案的计算开销。希望在未来的安全云存储方案设计中,相关研究人员能够避免出现相关数学运算上的问题,提高审计方案的正确性。
文中改进方案是基于ZSS方案的,与基于RSA的方案不同,相比文中方案具有更低的计算开销,但是在面对未来日益复杂的用户需求,后期要从以下两点进行改进:
(1) 文中方案没有考虑云存储文件的备份。如果云存储器遭受物理或者网络破坏,数据将受到威胁。下一步工作将融入多副本方案,改进数据存储的安全性。
(2) 文中方案目前不支持动态验证。下一步将结合MHT或者在多副本方案下结合MHT,改进出支持数据动态操作的数据完整性验证方案。
