模糊推理优化的抗遮挡PMBM跟踪算法

李翠芸,衡博文,谢金池

(西安电子科技大学 电子工程学院,陕西 西安 710071)

1 引 言

目标跟踪技术是通过传感器对特定区域内目标数量和位置等关键信息进行估计的技术。随着传感器分辨力的不断提高,目标跟踪算法逐渐由单一点目标跟踪发展到了多扩展目标跟踪,在对多个目标的运动状态进行跟踪的同时,还能够估计其扩展形状,从而具有了更大的实用价值。与联合概率数据关联、多假设跟踪[1-2]等传统算法相比,基于随机有限集[3]的目标跟踪算法不需要考虑目标和量测之间的数据关联,在减小计算复杂度的同时具有更高的跟踪精度,目前已经成为目标跟踪领域的研究热点[4-5]。其中,泊松多伯努利混合(Poisson Multi-Bernoulli Mixture,PMBM)滤波器[6]使用泊松点过程(Poisson Point Process,PPP)描述未检测目标,使用多伯努利混合分布描述已检测目标,在目标新生、死亡等复杂场景中也可以实现有效跟踪,近年来受到了学者们的广泛关注。

目标遮挡是多扩展目标跟踪中的常见问题。当目标之间的距离较近时,目标的扩展形状发生交叠,便产生了遮挡问题。此外,如果传感器的扫描区域内存在未知障碍物,也会出现目标被部分或全部遮挡的现象。如果多扩展目标跟踪算法不对这些特定场景进行考虑,在跟踪过程中将面临目标丢失的问题,从而导致对目标数量的估计产生偏差。为了解决目标遮挡引起的问题,目前已经有多种算法被提出,其中最为常见的是基于检测的方法。该类方法的核心思想是先通过检测判断目标是否被遮挡,再对处于遮挡情况的目标作进一步处理。文献[7]提出了一种在遮挡情况下基于归一化互相关的鲁棒目标跟踪方法,对未被遮挡的目标和被遮挡的目标进行不同的处理。文献[8]提出了一种基于置信度的遮挡检测算法,当检测到目标被遮挡且丢失跟踪中的目标时,算法会激活探测器以定位目标并继续跟踪。除此以外,另一类解决遮挡问题的算法是基于遮挡概率的方法。LAMARD等将目标的宽度作为遮挡条件来估计其遮挡概率,并将遮挡概率集成到势概率假设密度(Cardinalized Probability Hypothesis Density,CPHD)滤波器中[9]。文献[10]提出了一种激光测距仪量测条件下的具有遮挡处理能力的改进标签多伯努利(Labeled Multi-Bernoulli,LMB)滤波器。文献[11]提出了激光测距仪量测条件下的可变检测概率,用以解决泊松多伯努利混合滤波器的遮挡问题。在上述提出的算法中,目标遮挡概率的计算通常依赖特定种类的传感器提供的数据,并不能较好地适用于标准量测。文献[12]提出了一种使用贝塔分布模拟真实检测概率的BGGIW-PMBM算法。该算法虽然没有对遮挡问题进行特殊处理,但在可变检测概率的基础上能够被动地解决遮挡问题。在实际场景中,遮挡概率受到多种因素影响,具有非线性等特点,往往难以直接给出精确模型,而模糊系统可以从宏观角度充分利用模糊信息知识,形成易于处理的系统模型。因此,模糊系统能较好地解决非线性问题,具有广阔的应用和研究前景[13]。在目标跟踪领域内,模糊系统被广泛使用,许多学者都使用模糊系统对多目标跟踪算法进行了不同的优化[14-16]。

针对现有的泊松多伯努利混合算法在遮挡场景中不能稳定跟踪的问题,文中将模糊系统与基于高斯过程(Gaussian Process,GP)建模方法[17]的泊松多伯努利混合滤波器相结合,提出了一种模糊推理优化的抗遮挡高斯过程-泊松多伯努利混合滤波算法(GP-PMBM)。首先,针对扩展目标发生遮挡时的不同场景给出了相应的目标遮挡模型;其次,通过把可变检测概率加入状态空间的方式将遮挡对目标状态的影响考虑到算法滤波中;最后,将所构建的模糊推理系统与高斯过程-泊松多伯努利混合滤波算法结合,借助模糊系统的描述能力和泊松多伯努利混合滤波器的良好性能,实现对扩展目标的跟踪。实验结果表明,文中所提算法能够有效解决目标的遮挡问题,与现有泊松多伯努利混合滤波算法相比具有更高的精度。

2 目标遮挡模型

目标遮挡指目标在遮挡物的影响下部分或全部不可见。在跟踪过程中,目标发生遮挡时伴随着量测率的变化,从而导致滤波器对目标数量的错误估计。为了对目标遮挡过程进行描述,首先需要建立一个对应的目标遮挡模型。该模型建立的前提假设是目标的扩展形状不能被忽略,这与扩展目标跟踪的前提假设一致。在目标跟踪算法中,滤波器只能获得来自传感器的量测。假设传感器只产生目标所属类别的边缘量测,当目标被障碍物遮挡时,情形如图1所示。

图1 目标被障碍物遮挡示意图

从图1中可以看出,目标在遭遇障碍物时,传感器只能够获得目标未被遮挡部分的量测,而无法探测到被遮挡部分,显然此时目标的量测率会因为遮挡而下降。考虑将量测变化率作为衡量目标遮挡概率的一个因素,在第k时刻,量测变化率可表示为

(1)

其中,mk表示第k时刻算法所预测的与目标匹配的量测数量,nk表示第k时刻实际与目标匹配的量测数量。

在多扩展目标跟踪场景中,当目标之间距离过近时,会出现目标交叉导致互相遮挡的情况,如图2所示。

图2 目标间遮挡示意图

从图2中可以看出,右侧的目标2遮挡了左侧的目标1的一部分,在这种情况下传感器只能获得目标1未被遮挡部分的量测和目标2的全部量测。通常情况下,当两个目标质心距离越小时,越有可能发生目标间遮挡;反之,目标质心距离越大时,发生目标间遮挡的概率就越小。假设两目标质心之间的距离为d,采用多目标最短质心距离来衡量目标遮挡概率,可表示为

dm=min({di,j}) ,

(2)

(3)

其中,di,j表示目标i和目标j之间的质心距离,dmax表示最大距离。

3 可变检测概率模型

在随机集滤波框架中,检测概率是指监视区域内目标被传感器检测到的概率。通常假设目标的检测概率pD取决于目标状态,在仿真实验中用常数来近似。在此假设下,泊松多伯努利混合滤波算法没有充分考虑遮挡对目标状态的影响,进而产生在目标遮挡场景下的相应问题。本节对原有的泊松多伯努利混合目标状态空间模型加以改进,使目标的检测概率受遮挡影响而变化,进而把目标遮挡对目标状态的影响纳入到滤波步骤中,以实现泊松多伯努利混合滤波算法在遮挡场景下的稳定跟踪。

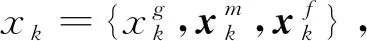
(4)

(5)

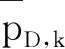
显然,目标的检测概率与遮挡概率具有负相关关系,将两者的关系表示为

(6)

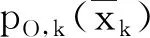
由文献[18]可知,泊松多伯努利混合滤波器在目标发生漏检时,有如下的目标存在概率更新公式:

(7)

(8)

其中,rk|k-1=pSrk-1,表示目标上一时刻的存在概率经过预测步骤后的取值。可以看出,当一个目标被遮挡时,通过降低它的检测概率可以减缓该目标的存在概率的下降速度,避免目标因存在概率太低而被滤波器剪枝,从而适当延长被遮挡目标的生存时间,以实现提升滤波器在遮挡场景下的跟踪性能的目的。

4 遮挡概率的模糊推理

从上面内容可以推测出目标遮挡概率与量测变化率和最短质心距离有关,但是仍难以构造线性模型对其直接计算。为了解决这个问题,可以通过构建相应的模糊推理系统使得到的可靠推理信息在计算遮挡概率时发挥作用。要构建一个模糊系统,首先需要确认模糊系统的输入和输出,再建立它们的隶属度函数,最后建立模糊规则。显然,将量测变化率和最短质心距离作为两个输入变量较为合适。一般来说,模糊集的数量越多,输出的精度越高,同时计算量就越大。对于量测变换率,其取值范围为[0,1],选择4个语言模糊集{VS,S,M,B}分别表示{非常小,小,中,大},以此来描述目标量测率的不同变化程度。其中,模糊集VS和模糊集B的隶属度函数采用梯形函数,模糊集S和模糊集M的隶属度函数采用三角形函数。对于最短质心距离,其取值范围为[0,10]m,选择与量测变化率相同的4个语言模糊集{VS,S,M,B}对应表示{非常小,小,中,大},以此来描述最短质心距离的大小。与量测变化率不同,其相关的隶属度函数主要采用三角形函数。两个输入变量的隶属度函数分别如图3、图4所示。

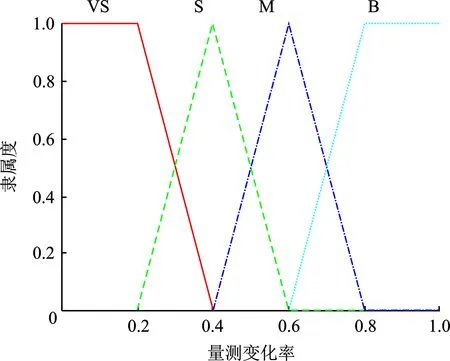
图3 量测变化率的隶属度函数

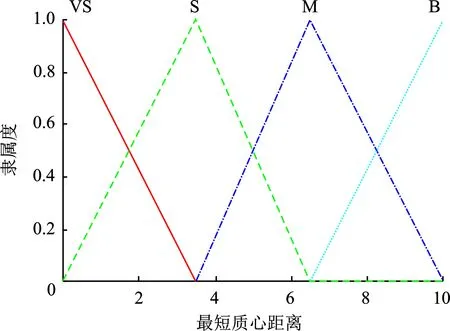
图4 最短质心距离的隶属度函数

首先,将该系统的输出变量设为遮挡概率。与输入变量不同,用5个模糊集来描述输出变量以获得更高的精度,遮挡概率的取值范围为[0,1],选择模糊集{VS,S,M,B,VB}分别表示{非常小,小,中,大,非常大}。输出变量的隶属度函数如图5所示。

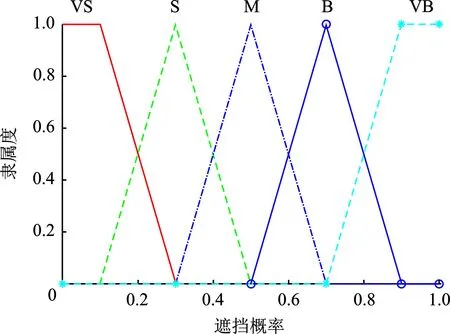
图5 遮挡概率的隶属度函数

接着,根据上述定义的两个模糊输入和一个模糊输出,可构建相应的16条模糊规则,如表1所示。表1中,pZ表示量测变化率,dm表示最短质心距离。

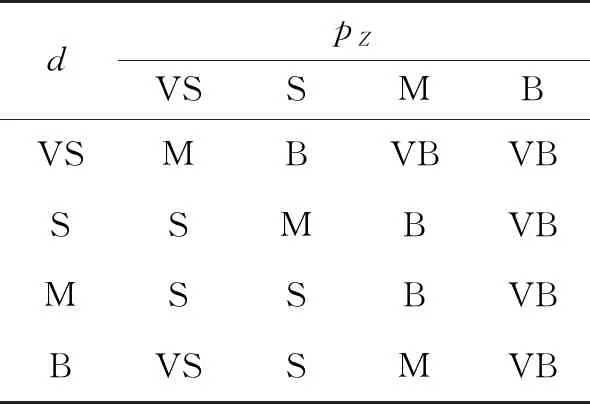
表1 模糊规则

最后,根据输入变量的隶属度函数和模糊规则,借助MATLAB软件中的模糊控制工具箱生成相应的模糊推理系统,如图6所示。

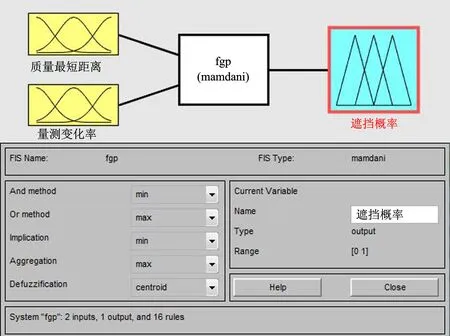
图6 使用MATLAB模糊控制工具箱生成模糊系统

5 模糊推理优化的GP-PMBM算法

通过将模糊推理系统融入高斯过程-泊松多伯努利混合滤波器,可以得到适用于遮挡场景的FGP-PMBM滤波器。滤波步骤包括预测、量测分组和划分、目标检测概率的估计、更新。

步骤1 预测。与GGIW-PMBM类似,FGP-PMBM的预测分为PPP预测和MBM预测两部分。其中,PPP项表示从未被检测到的目标,MBM项表示已经被检测到的目标。PPP预测的强度为

(9)

(10)

(11)

MBM预测的存在概率和空间分布为

(12)

(13)

步骤2 量测分组和划分。由于多扩展目标场景中量测集中的量测并非来自单个目标,且可能为不属于任何目标的杂波,因此无法直接进行更新,需要在更新前对量测进行分组和划分。量测分组通过设定门限将门限内的量测分配给同一个目标,门限的相关参数由目标的质心和形状范围确定,具体步骤参见文献[19]。在划分量测时,通常使用基于密度的含噪声空间聚类(Density Based Spatial Clustering of Applications with Noise,DBSCAN)算法,具有较高的准确度。

步骤3 目标检测概率的估计。利用第4节中的模糊推理系统估计目标的遮挡概率,进一步计算出目标的检测概率。为了减小计算量,只计算最有可能存在的目标的遮挡概率,主要包含权值较大的假设。同时,将权值较低的假设的目标遮挡概率设为0,根据式(6)计算目标当前时刻的检测概率。

步骤4 更新。PPP漏检部分的强度为

(14)

PPP漏检对应的目标参数分别为

(15)

(16)

PPP被检测到的部分转化为MBM,其存在概率和空间分布为

(17)

(18)

(19)

MBM漏检部分的存在概率和空间分布为

(20)

(21)

其中,

(22)

(23)

(24)

MBM漏检对应的目标参数为

(25)

(26)

MBM被检测到的部分存在概率和空间分布为

(27)

(28)

滤波步骤中其余参数的具体计算与文献[18]的一致,此处不再赘述。

6 仿真结果与分析

为了验证文中所提出的FGP-PMBM算法在不同遮挡条件下跟踪扩展目标的有效性,设计了两个不同的仿真实验,将FGP-PMBM算法与GP-PMBM算法、GGIW-PMBM算法[18]以及BGGIW-PMBM算法[12]进行对比。其中,实验1验证在实验场景内有固定障碍物时所提算法的有效性,实验2验证在两目标交叉发生目标间遮挡的场景下所提算法的有效性。在文中的所有仿真实验中,蒙特卡洛次数均为100,仿真实验平台为AMD Ryzen 7 5700G,CPU3.80GHz,MATLAB2020。

实验1设定监视区域为[0,200]m×[0,200]m,场景中包含一个目标,该目标的存活时间为60个时刻,目标的运动模型为CV模型,初始状态为x=[10,190,0,3,-3,0]T。场景中存在一个中心坐标位于[136,64]m,遮挡半径为10.5 m的遮挡物,目标在41时刻到45时刻之间共5个时刻被遮挡物遮挡,目标的运动状态转移矩阵Fm和过程噪声协方差矩阵Qm分别为

(29)

(30)

传感器接收到的量测和目标的真实运动轨迹如图7所示。图8是4种不同算法在该场景下的跟踪结果图。

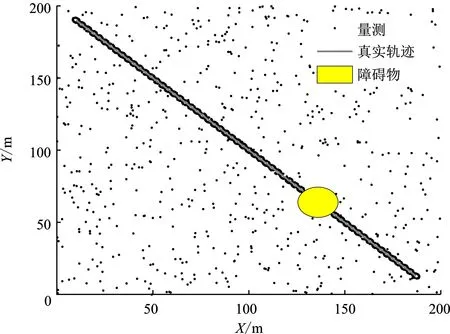
图7 实验1场景量测和目标真实轨迹

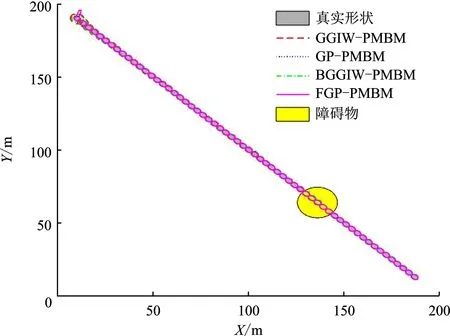
图8 实验1跟踪结果

图9为GGIW-PMBM、GP-PMBM、BGGIW-PMBM和FGP-PMBM算法的跟踪结果在目标被遮挡时刻左右的局部放大图,图10展示了4种算法在该场景下的目标数估计结果,图11和图12分别是4种算法的目标检测概率和存在概率估计。

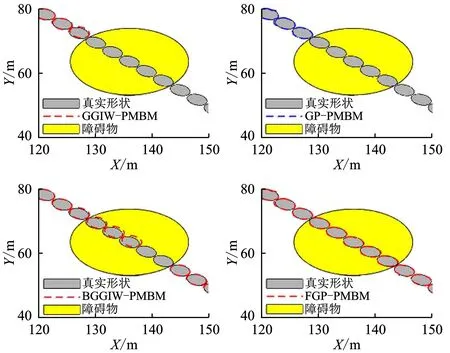
图9 4种算法跟踪结果的局部放大图

图10 实验1目标数估计

从图9可看出,FGP-PMBM在目标被遮挡时仍然持续地跟踪目标。BGGIW-PMBM在目标被遮挡的前3个时刻仍能跟踪目标,但在目标被遮挡的后两个时刻漏估目标,并在传感器重新获得目标量测后继续跟踪目标。GP-PMBM和GGIW-PMBM在目标被遮挡时丢失了目标,在遮挡消失后将此目标视为新生目标继续跟踪。图10中目标数的估计结果进一步验证了上述结论。

从图11、图12中可看出,GGIW-PMBM和GP-PMBM丢失目标的原因,较高的检测概率导致算法不能准确地估计被遮挡目标的存活概率,进而使目标的存活概率在漏检时迅速下降,并在达到滤波器的修剪阈值后被修剪。BGGIW-PMBM被动地逐渐降低了目标检测概率,并且在目标被遮挡的前3个时刻中,估计的目标存在概率仍大于0.5。但是在目标被遮挡的后两个时刻中,BGGIW-PMBM估计的目标存在概率下降至0.5以下,而导致漏估目标。由于存在概率没有达到修剪阈值,该目标的假设继续以伯努利项的形式存在,使得BGGIW-PMBM在场景中重新出现目标量测后继续跟踪。FGP-PMBM则充分考虑到目标被遮挡的可能,较快地降低了目标的检测概率。因此,FGP-PMBM估计的目标存在概率在同一时刻相比于BGGIW-PMBM的估计结果更高。FGP-PMBM算法在所有时刻中未漏估目标,这说明其对被遮挡目标存在概率的估计相较于BGGIW-PMBM的估计更加准确。

图11 实验1目标检测概率估计

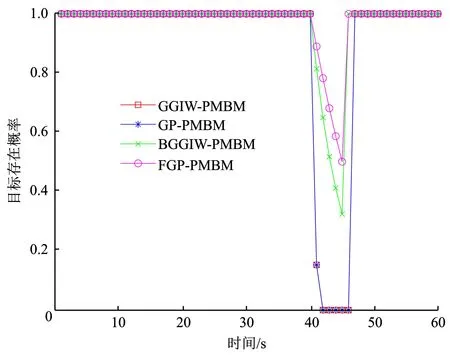
图12 实验1目标存在概率估计

图13给出了4种算法跟踪结果的质心OSPA。可以看出,当目标被障碍物遮挡时,GP-PMBM和GGIW-PMBM的OSPA距离误差立即大幅增加。BGGIW-PMBM在遮挡发生后的前3个时刻误差保持稳定,随后大幅增加,而FGP-PMBM在整个遮挡期间误差变化不大。其中,GP-PMBM和GGIW-PMBM的误差较高是因为算法在目标被遮挡后的所有时刻中丢失了目标,BGGIW-PMBM则因为有两个时刻漏估目标而表现弱于FGP-PMBM。实验结果表明,FGP-PMBM在场景中有固定遮挡物的情况下具有更高的跟踪精度。

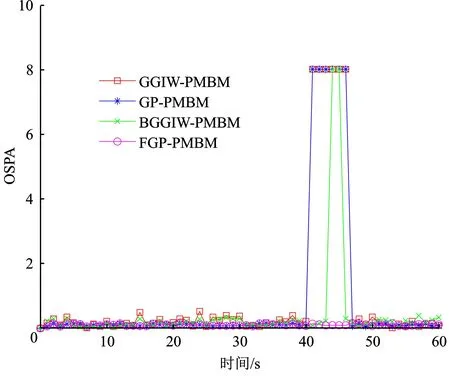
图13 实验1跟踪结果的质心OSPA

实验2设定监视区域为[0,250]m×[0,200]m,场景中包含了两个目标,且所有目标的存活时间皆为60个时刻,目标的运动模型为CV模型,初始状态分别为x1=[10,175,0,3.5,-2.5,0]T和x2=[10,25,0,3.5,2.5,0]T,两目标在31时刻交叉并发生了目标间遮挡。其他相关参数的设置与实验1相同。

该场景下传感器接收到的量测和目标的真实运动轨迹如图14所示,图15是该场景下GGIW-PMBM、GP-PMBM、BGGIW-PMBM和FGP-PMBM 4种算法的跟踪结果图,图16为3种算法的跟踪结果在交叉部分的局部放大图,图17是该场景下4种算法的目标数估计结果。

从图15可看出,GGIW-PMBM、GP-PMBM、BGGIW-PMBM和FGP-PMBM算法都完成了跟踪任务。从图16可看出,GP-PMBM和GGIW-PMBM在目标发生交叉的时刻漏估了被遮挡的目标2,误认为在该时刻只存在一个目标,BGGIW-PMBM以及FGP-PMBM在目标发生交叉时仍然准确地估计出场景中存在两个目标。图17进一步验证了上述结论。

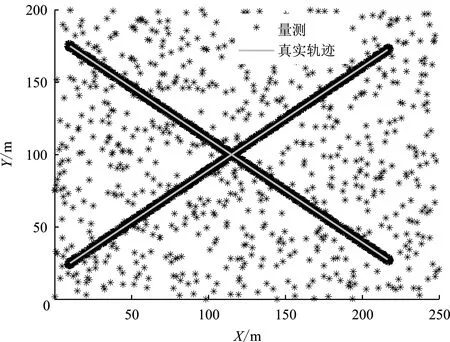
图14 实验2场景量测和目标真实轨迹

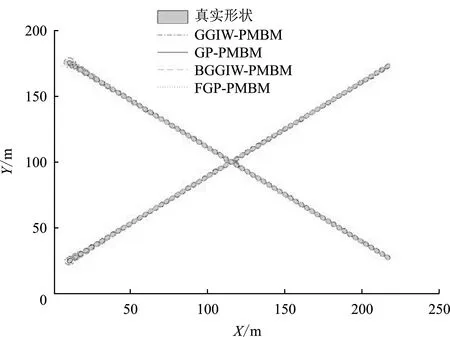
图15 实验2跟踪结果

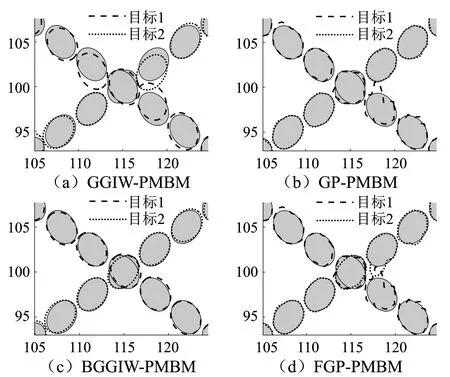
图16 4种算法跟踪结果局部放大图

图17 实验2目标数估计

图18至图21分别是4种算法跟踪目标1、目标2时的检测概率估计和存在概率估计。

图18 实验2目标1检测概率估计

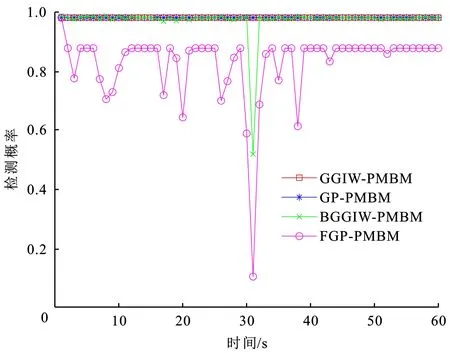
图19 实验2目标2检测概率估计

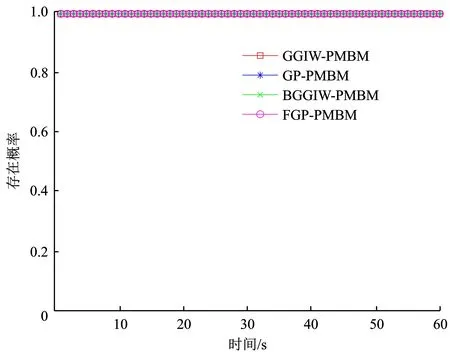
图20 实验2目标1存在概率估计

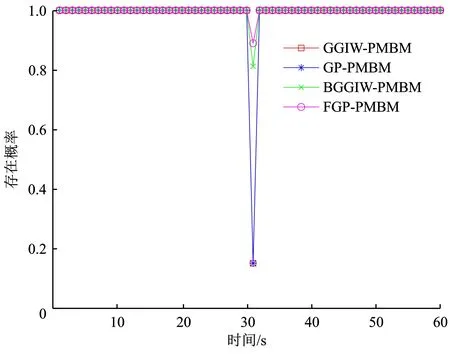
图21 实验2目标2存在概率估计

图22 实验2跟踪结果的质心OSPA

从图18、图19可以看出,GGIW-PMBM和GP-PMBM在交叉时刻维持固定检测概率,并没有对因目标遮挡而造成的目标漏检做出反应。FGP-PMBM基于对目标遮挡概率的计算快速降低了目标1和目标2的检测概率,BGGIW-PMBM则在该时刻因目标2漏检而被动地降低了目标2检测概率,但没有改变目标1的检测概率。从图21可看出,GGIW-PMBM和GP-PMBM错误估计了被遮挡目标的存在概率,它们估计的目标2的存在概率都低于0.5,从而导致了算法漏检。FGP-PMBM和BGGIW-PMBM则较慢地降低了被遮挡目标的存在概率,使算法能够准确估计目标数目。图22给出了4种算法跟踪结果的质心OSPA。

从图22可以看出,在目标交叉时刻GP-PMBM和GGIW-PMBM的误差较高,主要是由此时对场景中目标数目的错误估计导致的。与GGIW-PMBM、GP-PMBM、BGGIW-PMBM相比,FGP-PMBM在60个时刻内的OSPA均值分别降低了约65.05%、37.22%和38.94%。表2给出了该场景下4种算法的平均运行时间。

从表2可以看出,GGIW-PMBM的运行时间最短,FGP-PMBM由于加入了模糊推理系统,运行时间相较于GP-PMBM有所增加。

表2 4种算法的平均运行时间

7 结束语

文中主要针对GP-PMBM滤波算法在目标遮挡场景下的跟踪问题进行研究。首先根据不同的遮挡情况给出了对应的目标遮挡模型,并对PMBM滤波器的状态空间模型加以改进;然后基于量测变化率和最短质心距离构建了用于计算目标遮挡概率的模糊推理系统;最后将模糊推理系统与GP-PMBM滤波器相结合,提出了适用于遮挡场景的FGP-PMBM滤波器。仿真结果表明,文中提出的FGP-PMBM算法在面对障碍物遮挡和目标间遮挡时仍然能够维持较高的估计性能,充分验证了所提出的FGP-PMBM滤波器在遮挡场景下的优越性。