一种融合纵横时空特征的交通流预测方法

侯 越,郑 鑫,韩成艳

(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)

1 引 言

近年来,城市汽车保有量激增,道路网承载力不足,使得交通拥堵问题愈发严重。作为智能交通系统(Intelligent Transportation Systems,ITS)[1]的重要组成部分,交通流预测是信息诱导解决交通拥堵问题的主要技术手段。其通过挖掘多源数据中的隐藏特征,学习历史交通流的变化规律为ITS提供流量分配决策依据,从而为交通拥堵问题的解决提供智慧化的信息调配优化方案。

交通流预测经历了统计学模型[2-3]、传统机器学习模型[4-5]、深度学习模型3个阶段。其中,深度学习因其强大的非线性拟合能力和深层特征提取能力成为目前的主流模型,如典型的卷积神经网络(Convolutional Neural Network,CNN)[6-7]、长短时记忆网络(Long Short-Term Memory,LSTM)[8]、双向长短时记忆网络(Bidirectional Long Short-Term Memory,Bi-LSTM)[9]、门控循环单元(Gated Recurrent Unit,GRU)等。文献[10]利用LSTM提取断面交通流时序特征预测交通速度。文献[11]利用一维卷积网络提取断面交通流的空间特征,利用LSTM、Bi-LSTM分别提取交通流短期、长期时间依赖特征。上述研究虽有效预测了断面交通流,但未考虑上下游断面间的纵向时空特性与断面内部多车道间的横向时空特性对交通流预测的影响。文献[12]基于相似性度量与能量归一化捕捉到上下游断面间的时滞特性,并利用LSTM预测断面交通流。但该方法忽略了上下游断面间交通流传递与回溯的空间流动特性,未能充分挖掘上下游交通流潜在的纵向时空关系。文献[13]利用LSTM、GRU实现快速路车道级速度预测,基于信息熵的灰色关联分析有效提取了车道级交通流空间特征,然而该组合建模方式在提取时空特征时,割裂了交通流时空特性提取的一致性,对交通流横向时空关系捕捉不足。

针对上述问题,笔者提出一种融合纵横时空特征的组合深度学习交通流预测模型(Bidirectional Long Short-Term Memory-Multiscale Convolution group-Attention,Bi-LSTM-MConv-Attention)。通过计算延迟时间量化消除上下游断面间的交通流时滞特性;利用Bi-LSTM与向量拆分数据输入方式,捕捉消除时滞影响后上下游交通流双向的时序特征与空间流动特征,达到充分挖掘交通流纵向时空关系的目的。同时模型采用多尺度卷积群提取待预测断面内多车道多时间步下的横向时空特征。最后构建注意力融合模块关注纵横时空特征对交通流的动态影响,并输出最终交通流的预测值。

2 交通流纵横时空相关性分析

2.1 纵向时空相关性分析

纵向时空相关性是指具有纵向延伸分布位置关系的断面间,因交通流传播与回溯的空间流动性而引起的交通流时空关联关系。在纵向延伸分布位置关系中,上下游断面间的空间位置关系尤为典型。受空间位置关系及各车辆差异化驾驶行为的影响,上游交通流传递至下游会存在一定时延,这种在实际场景中普遍存在的现象称为空间时滞性。为了更清晰地说明该现象,选用2016年9月9日上午6点至下午18点,OpenITS合肥示范区2号和6号微波检测器数据来绘制监测断面的流量日折线图,如图1所示。2号、6号检测器分别位于路段上游和下游,具有纵向空间分布关系。由图1可知,2号和6号检测器监测断面的流量变化趋势高度一致,这充分说明上下游断面间存在较强的纵向时空关联关系。同时,2号检测器的流量较6号检测器始终提前抵达至波峰或波谷,这说明上下游断面间存在明显的空间时滞特性,这一特性会造成后续输入模型的数据存在误差,消除时滞性可增强上下游断面间交通流数据的时空相关关系,从而有效提高预测精度。

图1 检测器监测断面流量折线图(每5分钟一测)

2.2 横向时空相关性分析

横向时空相关性是指同一断面内车道级交通流数据间的相互关联影响,是空间关系中另一种较为普遍的结构分布。以OpenITS合肥示范区黄山路与天智路交叉口黄山路西进口断面为研究对象,分析断面内车道间交通流存在的横向时空相关性。图2为研究断面内部车道分布图,断面内包含5条车道:Htw001_1、Htw001_2、Htw002_1、Htw002_2、Htw002_3,各车道车辆行驶方向一致。选取5条车道于2016年9月10日上午6点至9月12日上午6点的流量数据,采用皮尔逊相关系数计算各车道交通流数据间的关联程度。表1为不同车道间皮尔逊相关系数计算结果,车道1～车道5依次为图2中的Htw001_1、Htw001_2、Htw002_1、Htw002_2、Htw002_3车道。一般来说,皮尔逊系数值在0.8～1.0为极强相关,0.6～0.8为强相关,0.4～0.6为中等程度相关,0.2～0.4为弱相关,0.0～0.2为极弱相关或无相关[14]。由表1可知,不同车道间的皮尔逊系数值多高于0.6,可见同一断面内车道级交通流具有较强的横向时空相关性。

图2 黄山路西进口内部车道分布图

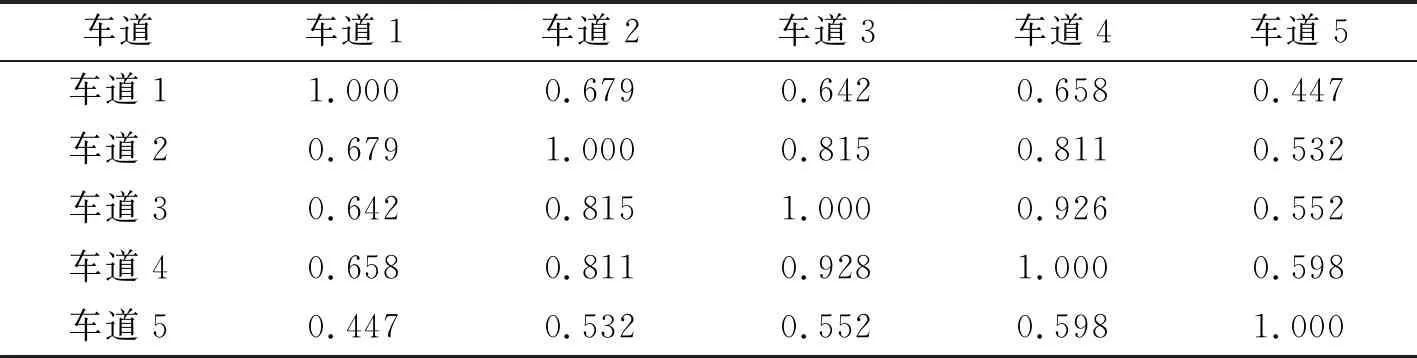
表1 车道流量间的皮尔逊相关系数

3 融合纵横时空特征的交通流预测模型

为充分挖掘交通流细粒化时空关系,笔者提出一种融合纵横时空特征的交通流预测模型(Bi-LSTM-MConv-Attention),图3为模型架构示意图。模型包括纵向时空特征提取模块、横向时空特征提取模块和注意力融合模块,旨在捕捉交通流纵向、横向时空特征以及纵横时空特征对交通流预测的影响。模型的输入包含上下游断面实测交通流序列与下游断面内多车道交通流数据,输出为注意力权重向量与纵横时空特征经点积运算得到的下游断面交通流预测结果。

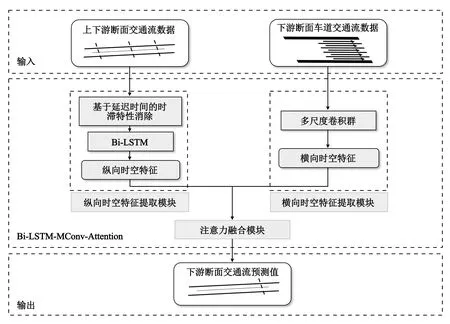
图3 Bi-LSTM-MConv-Attention模型架构图

3.1 纵向时空特征提取模块

该模块首先通过计算延迟时间量化消除上下游断面间交通流传递时的空间时滞影响,通过最佳时滞关系获得上下游断面强关联性的交通流序列。其空间时滞延迟时间的计算如下所示:

(1)

(2)

图4 Bi-LSTM结构图

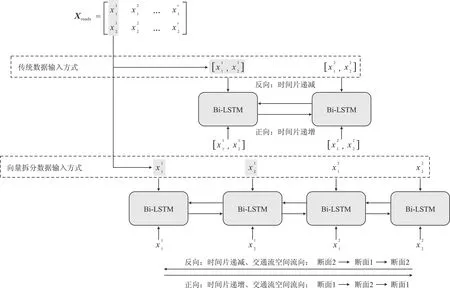
图5 传统数据输入方式与向量拆分数据输入方式下Bi-LSTM提取过程对比图

3.2 横向时空特征提取模块

该模块利用多尺度卷积群(Multiscale Convolution group,MConv)提取待预测断面内车道间交通流不同时间步下的横向时空特征。图6为多尺度卷积群的运算示意图,多尺度卷积群由多个卷积核尺度不同的一维卷积层并列组成。因卷积核尺度不一,多尺度卷积群可同时捕捉多时间步下各车道间交通流的时空关系,对横向时空特征的提取更为充分。多尺度卷积群的运算过程如下:

hcorri=ReLU(Wi*Xlanes+bi) ,

(3)

(4)

其中,Xlanes∈RT×N代表多车道交通流数据矩阵,T为时间维度;N表示车道数;hcorri为第i种尺度下卷积层提取到的横向时空特征;ReLU为ReLU非线性激活函数;Wi代表第i种尺度卷积层的卷积核权重矩阵;bi为偏置项;*表示卷积运算。m为多尺度卷积群中卷积核尺度类别数;Hcorr为多尺度卷积群最终提取到的各车道间的横向时空特征,其由各尺度卷积层提取到的横向时空关系加和得到。

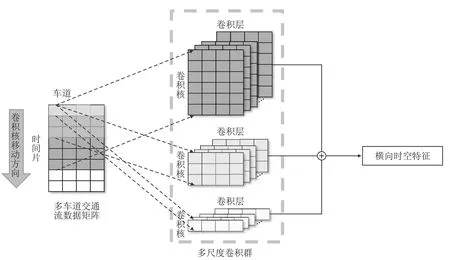
图6 多尺度卷积群运算示意图

3.3 注意力融合模块

为综合考虑交通流纵横时空特征对待预测断面交通流的影响,模块引入注意力机制[17]对纵横时空特征进行动态融合,并通过点积运算输出最终预测值。注意力机制计算过程如下:

H=WX+b,

(5)

α=softmax(H) ,

(6)

y=α·X,

(7)

其中,X=[x1,x2,…,xn]为输入向量,W为权重矩阵,b为偏置项,·为点积运算。首先,X经W训练拟合捕捉X对输出值的影响,得到隐藏层输出H;然后,利用softmax函数对H进行指数归一化操作,得到输入向量中各元素对输出值的重要程度,即注意力权重向量α=[α1,α2,…,αn];最后,由X与α经点积运算得到注意力关注下的预测输出值y。 文中模块的输入向量为纵横时空特征拼接向量,输出值y即为融合纵横时空特征后的交通流预测值。

4 实验及分析

实验中断面交通流数据源于OpenITS合肥示范区2号和6号微波检测器采集到的交通流数据。图7为检测器位置分布图,2号和6号检测器分别位于路段上游和下游,两检测器间直线距离为1.5 km,依据节3.1式(2)可知上下游断面间的时延约为2 min。车道交通流数据源于该示范区视频检测器采集的车道级交通流数据,覆盖6号检测器监测断面内的5条车道:Htw001_1、Htw001_2、Htw002_1、Htw002_2、Htw002_3,依据节2.2横向时空相关性分析结果,选择时空关联性更强的4条车道:Htw001_1、Htw001_2、Htw002_1、Htw002_2为研究车道。数据集时间跨度为2016年9月9日至10月8日,实验预测对象为下游6号检测器监测断面的交通流量。

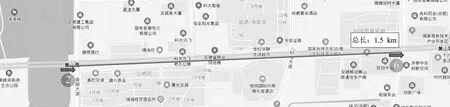
图7 断面检测器位置分布图

4.1 评价指标

为验证各模型的预测效果,实验选取平均绝对误差RMAE(Mean Absolute Error,MAE)、均方根误差RRMSE(Root Mean Square Error,RMSE)和决定系数R2(Coefficient of Determination)作为模型评价指标。其中,RMAE、RRMSE值越小,模型预测效果越佳;R2值越大,模型预测效果越佳,R2值域在[0,1],值为1表示模型预测无误差。它们的计算公式如下:

(8)

(9)

(10)

4.2 参数设置

实验中模型输入数据的时间窗大小为12,即利用一小时12个时间片的历史交通流来预测未来交通流。实验训练轮数为100,批次数为48,学习率为0.001,采用自适应矩估计(Adaptive moment estimation,Adam)优化器与均方差损失函数优化训练误差。模型中Bi-LSTM层隐藏单元个数为64,多尺度卷积群的卷积层尺度分别为6、3、1,各尺度卷积层层数为2。每层卷积后均有一层Dropout相连,目的是降低特征提取的过拟合现象。

4.3 实验结果分析

为评估所提模型的预测效果,实验将所提模型与时序预测中常用的LSTM、Bi-LSTM模型进行对比,同时增加了纵横时空特征及注意力机制的消融实验。实验结果如表2所示。

表2 模型单步预测效果

由表2可知,LSTM模型的平均绝对误差、均方根误差均高于其他模型,且R2最低,预测效果最不理想;Bi-LSTM模型的预测误差略低于LSTM,这是由于Bi-LSTM模型的双向特征学习结构,该结构可充分考虑两个方向的交通流变化规律,较之单向LSTM具有挖掘特征更充分的优势。相较于Bi-LSTM模型,Bi-LSTM+纵向时空特征模型的平均绝对误差和均方根误差分别降低了约4.51%和2.18%,R2也有一定程度的提高,可见对纵向时空相关性的考量可有效提高模型的预测精度;而LSTM+纵横时空特征、Bi-LSTM+纵横时空特征模型的预测效果较Bi-LSTM+纵向时空特征模型有显著提升,这是由于综合考虑纵横时空特征有助于挖掘交通流细粒化的时空关系,从而提高预测精度;Bi-LSTM-MConv模型预测效果较优,其平均绝对误差、均方根误差值分别约为 3.973、5.658,R2值约为0.964 39,但其预测误差仍高于笔者所提的Bi-LSTM-MConv-Attention模型,这充分说明所提模型中的注意力融合模块丰富了模型对交通流纵横时空特征的动态关注,进一步提高了预测精度。图8为各模型在测试集上预测值与真实值的对比图,结合图8可知,相比其他基准模型,所提Bi-LSTM-MConv-Attention模型的预测曲线与真实值曲线更为贴近,预测效果更优。

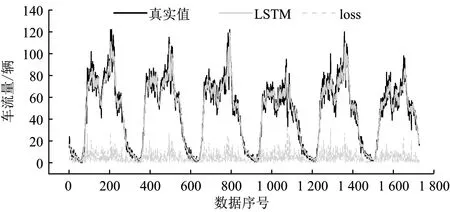
(a) LSTM

(b) Bi-LSTM

(c) Bi-LSTM+纵向时空特征

(d) LSTM+纵横时空特征

(e) Bi-LSTM+纵横时空特征

(f) Bi-LSTM-MConv

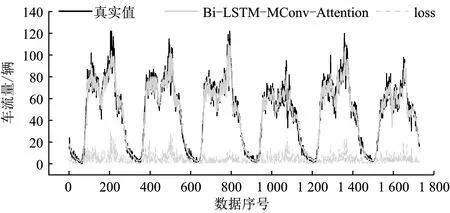
(g) Bi-LSTM-MConv-Attention

为进一步验证所提模型的普适性,增加了中长时多步预测对比实验,各模型在多步预测场景下的实验结果对比如图9所示。分析图9可知,笔者所提模型在各个预测步长下的RMAE、RRMSE始终最低,R2则最高,充分说明模型在中长时多步预测兼具优越性,且模型更稳定。

(a) RMAE

(b) RRMSE

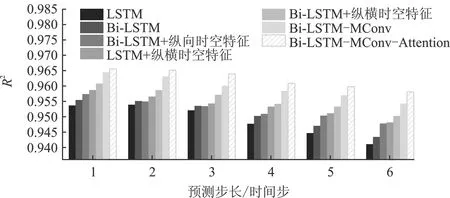
(c) R2

5 结束语

为充分挖掘交通流序列纵横向时空特征,增强交通流预测模型的精度和稳定性,笔者提出了一种融合纵横时空特征的交通流预测方法。该方法首先通过计算时延参数,并利用该参数加调上游交通流序列时间戳的方式来消除空间时滞影响,以增强交通流序列的纵向相关性。接着通过Bi-LSTM和改进的向量拆分数据输入方式提取到上下游交通流的纵向时空特征;利用MConv捕捉了车道级交通流在不同时间步下的横向时空特征。最后引入注意力机制融合纵横向时空关系,并通过注意力权重向量与纵横时空特征的点积运算得到最终的预测值。实验结果表明,所提方法的预测精度优于其他对比方法,在单步预测和多步预测中,进一步证明了该方法在实际路网拥堵背景下,能够精确、稳定地评估路网交通运行状态的事实,为ITS系统功能升级和交管部门信息化智慧诱导方面提供了有效的技术支撑。