线性分布式定向阵列波束空间覆盖面积分析

段柏宇,杨 健,陈 聪,郭文博,李 彤,邵士海

(1.电子科技大学 通信抗干扰全国重点实验室,四川 成都 611731;2.电磁空间认知与智能控制技术实验室,北京 100089;3.北京理工大学 网络空间安全学院,北京 100081)

1 引 言

相控阵天线因其高增益、高可靠性、波束指向灵活等优点,已广泛应用于军事探测、干扰、天气探测以及民用通信等领域[1-4]。考虑天线体积、部署地形、设备功耗等因素的限制,在某些场景下需要多部天线分布式部署,进行协同波束合成,以获得与单部天线相比更高的功率增益。分布式波束合成利用多个分布式节点形成虚拟天线阵列,通过调整各阵元的相位收发同一信号,合成定向波束[5]。

近年来,已有文献对分布式波束合成的问题进行了初步研究。针对分布式节点的振荡器误差对于分布式波束合成的影响,文献[6]运用核密度估计方法对其进行了研究。文献[7]讨论了参考振荡器和锁相环产生的相位噪声来源,进而分析相位噪声、更新间隔与分布式波束形成性能的相互关系。文献[8-10]对分布式波束合成功率优化问题进行了研究,其中,文献[9]建立了一个多目标优化框架,对移动无线传感器网络中分布式波束合成的最大旁瓣电平、分布式节点的传输功率以及运动能耗进行了联合优化。文献[11-12]研究了分布式节点间的同步问题,文献[11]给出一种两步相位同步算法。文献[12]基于节点共识优化概念,提出的分布式波束合成同步方法可用于同步开环分布式阵列中的节点。

文中考虑天地波束合成场景,地面部署的线性分布式定向阵列(多个定向阵列天线沿直线排布),与在近地轨道及以上高度(高度大于200 km)运行的卫星及航天器进行通信,或对其进行跟踪侦察、干扰。运用空间解析几何,提出一种线性分布式定向阵列波束(包括主瓣波束与栅瓣波束)在特定高度平面上增益覆盖面积的解析计算方法。通过该计算方法分析可知,阵列的俯仰角、目标平面高度、信号载频、分布式节点个数以及定向阵列间的间距与增益覆盖面积相关。其中,俯仰角、高度、载频及节点个数与波束合成的增益覆盖面积强相关,而间距对于增益覆盖面积(包括主瓣及栅瓣覆盖面积)的影响较小。

2 系统场景及模型

2.1 场景描述

图1为线性分布式定向阵列发射波束合成示意图。图1中每个地面移动平台搭载一个作为定向阵列的矩形阵列天线,呈等间距直线排列,且移动平台间距至少大于10倍信号波长。定向阵列的各阵元以不同的加权值发射同一信号,形成定向波束。各定向阵列的定向波束在一定高度截面上合成,投射出一片增益区域,如图1中椭圆区域所示。需要注意的是,根据天线互易定理[13],该区域同样是线性分布式定向阵列作为接收阵列时的增益区域。文中主要目的是研究该增益区域的覆盖面积与线性分布式定向阵列参数(如阵元间距、载频、个数等)之间的关系。

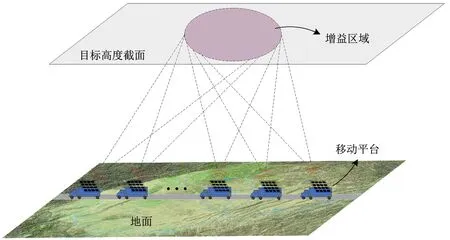
图1 线性分布式定向阵列发射波束合成示意图

2.2 线性分布式定向阵列波束方向图

图2 球坐标系示意图

首先建立如图2所示的球坐标系,点X(r,φ0,θ0)为坐标空间中任意一点,其中r表示点到坐标原点O的距离,θ∈[0,π]为俯仰角,φ∈(-π,π]为方位角。考虑到增益区域至少应用于距离阵列数百公里外,因此增益区域可视作线性分布式阵列的远场区域。根据阵列方向图乘积定理[13],线性分布式定向阵列的方向图可表示为

BC(φ,θ)=|Brect(φ,θ)||Bline(φ,θ)| ,

(1)

其中,Brect(φ,θ)表示单定向阵列的方向图,Bline(φ,θ)为线性分布式阵列的方向图。令定向阵列与其组成的线性分布式线阵的期望波束合成方向一致,即定向阵列与线性分布式阵列期望合成方向均为(φ0,θ0)。下面首先计算定向阵列方向图Brect(φ,θ)的解析式。

假设空间内存在N个全向阵元,令第1个阵元位于坐标原点,其位置p1=(0,0,0)T。第n个阵元在直角坐标系中的位置pn=(xn,yn,zn)T,其在(φ,θ)方向上的方向矢量a=[sinθcosφ,sinθsinφ,cosθ]T,相较于坐标原点信号的距离差dn=aTpn。因此,第n个阵元相对于原点的相位响应为

(2)

其中,λ表示信号波长。对全向阵元的阵列,采用均匀幅度加权,其在期望方向(φ0,θ0)上波束方向图可以定义为[14]

(3)

(4)

将式(4)代入式(3),得到均匀矩形阵列在期望方向(φ0,θ0)上的波束方向图为

(5)

利用等比数列求和公式以及欧拉公式,式(5)矩形定向阵列Brect(φ,θ)的解析式可进一步化简为

(6)

对于线性阵列,令L个定向阵列均匀排列在x轴线上,定向阵列间的间距均为D,则第l个定向阵列的坐标为pl=((l-1)D,0,0)T,其中1≤l≤L,l∈Z。 与均匀矩形阵列推导类似,均匀线阵在期望方向(φ0,θ0)上的波束方向图解析式为

(7)

将式(6)和式(7)代入式(1),便可求出线性分布式定向阵列的方向图。

3 线性分布式定向阵列覆盖面积分析

本节对线性分布式定向阵列波束在三维空间特定高度的覆盖面积进行理论分析推导。首先推导了线性分布式定向阵列的波束(包括主瓣波束与栅瓣波束)在高度横截面增益覆盖范围的解析式,然后对总的覆盖范围的面积进行近似计算。

3.1 线性分布式定向阵列横截面分析

3.1.1 单定向阵列波束横截面解析式

图3 单定向阵列波束在 三维空间的示意图

在阵列远场的场景下,矩形阵列的主瓣波束在三维直角坐标系内为一顶点在坐标原点O的椭圆锥,如图3所示。图3中箭头表示椭圆锥轴线方向,即波束期望方向。注意到,锥底椭圆的长轴在φ=φ0的俯仰平面上,设点A为锥底椭圆长轴靠近xOy平面的端点,点B为长轴的另一端点,锥底椭圆的短轴JK与AB相交于中心点C。为便于后文计算,令点A位于高度为h的横截面内,即点A的高为h。

波束宽度用两个平面来表示,第1个是相对于φ=φ0的俯仰平面,第2个是垂直于该俯仰平面,过锥底椭圆短轴的平面。令两个平面内的波束宽度分别为Θmain与Φmain,当一个大阵列调向到接近阵列法线方向时,Θmain可以近似表示为[14]

(8)

其中,Θx0是P元线阵法线方向(即θ0=0°时)的波束宽度,Θy0是Q元线阵法线方向的波束宽度。后文重点分析定向阵列为具有相等可分离权值方阵时的情况,即P=Q。若采用3 dB波束宽度,有Θx0=Θy0≈0.891λsecθ0/(Pd)=1.782/P。根据文献[14]中3 dB波束宽度的计算方法,若采用1.5 dB波束宽度,有Θx0=Θy0≈0.64λsecθ0/(Pd)=1.28/P。 对于方阵,将Θx0=Θy0代入式(8),可以得到Θmain=Θx0secθ0=Θy0secθ0。垂直平面的波束宽度可表示为[14]

(9)

对于方阵,式(9)化简为Φmain=Θx0=Θy0。注意到波束宽度Θmain与Φmain均与方位角φ无关。

首先考虑计算期望方向为定向阵列法线方向时,即(φ0,0°)时,波束截面的解析式。由于θ0=0°,对于方阵有Θmain=Φmain=Θx0=Θy0,此时椭圆锥的波束变为以z轴为轴线的圆锥。因此在法线方向,高度为h的横截面为圆,横截面的解析式为

(10)

图4 φ=φ0时,定向阵列俯仰平面示意图

所以,横截面椭圆的长轴可以表示为

(11)

横截面椭圆的短轴计算较为复杂,下面给出计算过程。首先根据图4中几何关系可得

LOC=hcos(Θmain/2)sec(θ0+Θmain/2),LOC′=hcos(Θmain/2)[sec(θ0+Θmain/2)+sec(θ0-Θmain/2)]/2,

LAB=2hsin(Θmain/2)sec(θ0+Θmain/2),LJK=2htan(Φmain/2)cos(Θmain/2)sec(θ0+Θmain/2)。

因为LA′B′∥LAB,LJ′K′∥LJK,所以有

(12)

因此,图4右下椭圆截面的长轴与短轴分别为

(13)

令C′为原点,C′A′方向为x轴正向,C′J′为y轴正向,建立平面直角坐标系,右下椭圆截面的解析式可以写为x2/m2+y2/n2=1,其中

(14)

令c=LC′G=hsin(Θmain/2)[(sec(θ0+Θmain/2)-sec(θ0-Θmain/2)]/2,那么点G在该平面直角坐标系下的坐标为(c,0),将该坐标代入右下椭圆截面解析式,可求得横截面椭圆(右上椭圆)的短半轴长度:

(15)

通过上文的计算,已求得横截面椭圆的长半轴、短半轴以及中心点坐标。需要注意的是,横截面椭圆中心并不在原点,需进行平移与旋转得到。根据坐标的平移以及旋转变化方法[15],沿原点旋转角度φ0,且沿x轴平移x0,沿y轴平移y0,高度为h时,定向阵列非法线方向波束的横截面解析式为

(16)

其中,x0=hcosφ0[tan(θ0+Θmain/2)+tan(θ0-Θmain/2)]/2,y0=hsinφ0[tan(θ0+Θmain/2)+tan(θ0-Θmain/2)]/2,a=h[tan(θ0+Θmain/2)-tan(θ0-Θmain/2)]/2,b=htan(Φmain/2)cos(Θmain/2)(sec(θ0+Θmain/2)sec(θ0-Θmain/2))1/2。

由式(16)可知,法线方向高度为h横截面的解析式为非法线方向的特殊情况。另外,由椭圆面积公式易知,单定向阵列波束横截面面积S=πab。

3.1.2 线性阵列波束横截面解析式

(17)

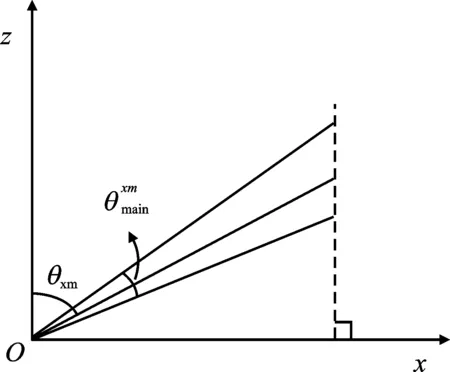
(a) 一维线阵zOx平面波束示意图

(b) 一维线阵φ=φ0平面波束示意图

因此,在高度为h的横截面的解析式可表示为

(18)

由此可知,一维线阵波束与横截面的交线解析式为两条双曲线。

3.2 线性分布式定向阵列横截面分析

本节对线性分布式定向阵列波束在特定高度的增益覆盖面积进行计算,主要思想是分别计算主瓣与各栅瓣在高度截面上的增益区域,再累加得到总的增益覆盖面积。

根据方向图乘积定理,结合3.1节分析,线性分布式定向阵列的一个波束在任意高度截面产生的增益区域可以定义为两条双曲线与定向阵列主波束椭圆截面所围成的区域。但需要注意的是,若定向阵列与线阵的波束宽度均选择3 dB波束宽度,那么该区域面积为实际分布式合成波束3 dB增益覆盖面积的一个上界,即分布式合成波束实际3 dB增益区域的面积不会超过该区域面积。因为该区域为单个定向阵列3 dB增益区域与分布式线阵的3 dB增益区域相叠加,区域内的归一化增益范围为-6 dB至0 dB,该区域一定包含实际的3 dB增益区域,而位于该区域外侧的增益则一定小于-3 dB。类似地,若定向阵列与线阵的波束宽度均取1.5 dB波束宽度,那么该区域面积为实际分布式合成波束3 dB增益覆盖面积的一个下界。区域内的归一化增益范围为-3 dB～0 dB,实际的3 dB增益区域一定包含该区域,位于该区域内侧的增益则一定大于-3 dB。

3.2.1 定向阵列合成波束不经过zOy平面

(19)

因此,对于角度范围为0<θL<θR<π/2,Λ,在合成方向为θ0和φ0时,θ空间的3 dB波束宽度为

(20)

类似地,θ空间的1.5 dB波束宽度可以表示为

(21)

θm=arcsin[sinθ0-mλ/(Dcosφ0)] 。

(22)

由式(22)可知,当m=0时,有θ=θ0,表示主瓣波束的位置。

(23)

解得

(24)

在已知阵列各参数的情况下,将线性阵列波束的两条双曲线解析式分别与定向阵列波束的椭圆截面解析式联立,代入相应的参数,便可求得双曲线与椭圆的交点:

当式(25a)取加号时,设其与式(25b)联立后可能的交点为a(x1,y1),b(x2,y2);当式(25a)取减号时,设可能的交点为c(x3,y3),d(x4,y4)。需要注意的是,在集合Λ的条件下,波束的两条双曲线与椭圆截面的交点个数,即式(25)解的个数,可能有0～4个。下面分别进行讨论。

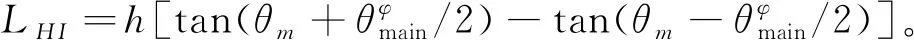
(26)

(a) 0个或1个交点

(b) 2个或3个交点

(c) 4个交点

(27)

因此,若有4个焦点,则波束覆盖面积的上界(或下界)可近似为

(28)

对主瓣与栅瓣形成的增益区域面积的上界(或下界)累加,便得到线性分布式定向波束的增益覆盖面积的上界(或下界)。

3.2.2 定向阵列合成波束经过zOy平面

对于定向阵列合成波束经过zOy平面的情况,由于定向阵列可视区域较小,文中仅分析φ0=±π/2时的增益覆盖面积,即定向阵列形成的椭圆截面关于y轴对称时的覆盖面积,其余情况的面积均可以近似为当φ0=±π/2时,对应θ0的覆盖面积。当φ0=±π/2时,分布式线阵的合成方向图化简为

(29)

(30)

(31)

式(31)方程组第1个方程是将φ0=±π/2代入式(18)得到。对于主瓣的截面覆盖面积,可以用上文提到的4个交点的面积计算方式进行计算。对于栅瓣,由式(30)可知,主瓣为法线方向时的栅瓣关于主瓣对称,因此仅需计算x轴正半轴的栅瓣形成的覆盖面积,再乘以2便可得栅瓣总的增益覆盖面积。正半轴栅瓣波束截面解析式与定向阵列波束截面的解析式联立如下:

(32)

上述方程组解的个数,仍可能有0～4个,栅瓣的覆盖面积的计算方法同样可以用上文提到的4个交点的面积计算方式进行计算。

4 仿真结果与分析

本节对线性分布式定向阵列合成波束在空间中的增益覆盖面积,与阵列的俯仰角、目标平面高度、信号载频、分布式节点个数以及定向阵列间距之间的关系进行仿真分析验证。表1是仿真参数设置,后文若未特别说明,则均默认使用该表中的参数。仿真中将对比定向方阵边长阵元个数P=50,100时的覆盖面积,根据Θx0=1.782/P,有Θx0=2°,1°,即对比定向方阵法线方向的3 dB波束宽度为1°与2°时的覆盖面积。另外,仿真中对波束增益进行了归一化,覆盖面积均为3 dB波束宽度的增益覆盖面积。

首先简要说明文中所提方法的计算流程,下文仿真图中线性分布式定向阵列的解析值上界与下界均按照该流程得出。计算时已知表1中阵列参数。

表1 仿真参数设置

(1) 按照式(8)、式(9)分别计算单定向阵列俯仰平面与垂直平面的波束宽度Θmain与Φmain。

(2) 按照式(16),计算参数x0,y0,a,b,得到高度为h时,定向阵列非法线方向波束的横截面解析式。

(3) 判断定向阵列合成波束是否经过zOy平面。

(a) 若定向阵列合成波束不经过zOy平面:

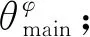
② 按照式(22),计算在φ=φ0平面处,θ空间的俯仰角θm。

④ 解式(25)方程组,根据解的个数进行如下操作:若解有2或3组,则按照式(26)计算波束覆盖面积的上界(或下界),且m=m+k,返回②;若解有4组,则按照式(28)计算波束覆盖面积的上界(或下界),且m=m+k,返回②;若无解或仅有1组解,停止计算。

此时已得到波束主瓣及主瓣正侧栅瓣形成的覆盖面积的上界(或下界)。

⑤ 令m=-1,k=-1,重复②～④,求得主瓣负侧栅瓣形成的覆盖面积的上界(或下界)。

⑥ 对所求主瓣及所有栅瓣的面积累加。

图7展示了当θ0=π/4,φ0=π/4时,单定向阵列波束以及线性分布式定向阵列波束在高度为500 km时的横截面仿真图。图中椭圆表示波束宽度为1.5 dB和3 dB时,定向阵列波束在截面上的解析区域。对比图7(a)与图7(b)可知,线性分布式定向阵列的3 dB波束覆盖面积明显小于单定向阵列的3 dB波束覆盖面积(但绝对增益会更大)。另外,由图7(b)图像可以看出,其增益区域的形状与前文理论分析一致,每个波束形成的条形覆盖区域为曲率很小的两条双曲线与椭圆所围成的区域。

(a) 单定向阵列横截面图像

(b) 线性分布式定向阵列横截面图像

图8考察单定向阵列波束在不同高度、不同俯仰角与3 dB波束覆盖面积的关系(在俯仰角与覆盖面积的关系图中,期望方位角为φ0=π/4)。其中THETA为2°表示定向方阵法线方向的3 dB波束宽度为2°,THETA为1°表示定向方阵法线方向的3 dB波束宽度为1°。图中覆盖面积的解析值曲线与仿真值曲线几乎重合,解析值是根据式(16),利用椭圆面积公式求出的。由图8可知,随着截面高度、俯仰角度增加,3 dB波束覆盖面积不断增加。

(a) 截面高度与覆盖面积关系图

(b) 俯仰角与覆盖面积关系图

图9是线性分布式定向阵列波束在不同高度、不同俯仰角时与覆盖面积的关系曲线(在俯仰角与覆盖面积的关系图中,期望方位角为φ0=π/4)。同样,图中覆盖面积的解析值上下界与仿真值上下界几乎重合。需要注意的是,图9中覆盖面积的解析值是由覆盖面积解析值上界加上解析值下界的和再除以2得到的。由图9可知,所求出的覆盖面积解析值与仿真值几乎一致。因此在工程实践中,可以用该方法直接估算线性分布式定向阵列的实际增益面积。关系曲线表明,随着截面高度、俯仰角度增加,波束的覆盖面积不断增加。

(a) 截面高度与覆盖面积关系图

(b) 俯仰角与覆盖面积关系图

图10(a)是线性分布式定向阵列不同阵列间距与覆盖面积关系图。图中阵列间距的仿真范围为10 m～1 000 m。如图10(a)所示,改变分布式阵列的间距对覆盖面积的影响很小。这是因为虽然增大阵列间距会导致合成波束宽度变窄[14],单个波束覆盖面积减小,但增大分布式阵列的间距,同时会使得定向阵列的可视区域内出现更多的波束栅瓣,因此总的波束覆盖面积几乎不受阵列间距影响。图10(b)展示了线性分布式定向阵列不同载频与覆盖面积关系图。图中载频的仿真范围为0.3 GHz～10 GHz。由图10(b)可知,随着载频的提高,线性分布式定向阵列的覆盖面积总体呈现下降趋势,这是因为当分布式阵列间距D一定时,增加载频会减小分布式阵列合成的波束宽度[14]。但是,图中的面积并不是完全随着载频提高而下降,这同样是因为增加载频的同时会导致在定向阵列的可视区域内出现更多的波束栅瓣,在较高载频时,总的波束覆盖面积变化不大。

(a) 阵列间距与覆盖面积关系图

(b) 信号载频与覆盖面积关系图

图11考察了线性分布式定向阵列不同阵列个数与覆盖面积的关系。图11表明,增加分布式定向阵列的个数会降低线性分布式定向阵列的3dB波束覆盖面积,这是因为增加阵列个数会减小3dB波束宽度[14]。与增加间距或载频不同,增加阵列个数并不会增加栅瓣的个数,这由栅瓣位置表达式(22)可知,式(22)中的θm与定向阵列个数L无关。因此,增加定向阵列个数会显著地降低线性分布式定向阵列的3 dB波束覆盖面积。另外,图中两条黑色曲线相对值表示不同阵元个数的分布式阵列实际增益,大于四阵元阵列最大增益值(即12.04 dB)的相对增益覆盖面积。这两条曲线说明,增加定向阵列个数虽然会降低阵列的3 dB波束覆盖面积,但使得实际相对增益覆盖面积大幅增加(实际增益增大),且在特定阵列个数下取得当前相对增益面积的最大值。

图11 线性分布式定向阵列不同阵列个数与覆盖面积的关系图

5 结束语

笔者利用阵列波束合成原理以及空间解析几何,提出一种针对线性分布式定向阵列波束在特定高度平面上增益覆盖面积的理论解析计算方法。通过建模分析与数值仿真结果可知,线性分布式定向阵列合成的归一化3 dB波束增益覆盖面积(该面积包括主瓣覆盖面积与栅瓣覆盖面积)随着阵列俯仰角、波束合成高度的增加而扩大,随着信号载频以及分布式节点个数的增加而缩小。另外,定向阵列间的间距,几乎不会影响增益覆盖面积。这是因为改变阵列间距虽然会影响合成波束宽度,但同样会影响栅瓣在可视区域内的个数。文中所提方法的解析值与计算机仿真值相符,可以为远距离大功率分布式阵列的工程实现提供理论参考。