计及能量共享的5G基站电能实时调度优化策略
2023-11-17刘迪迪杨玉荟肖佳文杨益菲程鹏鹏张泉景
刘迪迪,杨玉荟,肖佳文,杨益菲,程鹏鹏,张泉景
(1.广西师范大学 电子与信息工程学院,广西 桂林 541004;2.西华师范大学 教育信息技术中心,四川 南充 637001)
1 引 言
近年来,物联网、大数据等新兴业务的快速发展,对通信技术提出更高要求,具有高速率、高连续性及高可靠性等特点的第5代移动通信(the 5th Generation mobile communication,5G)被视为满足新兴业务发展需求的核心技术。然而,第5代移动通信网络带来高性能通信质量的同时,对基站的部署密度要求更大(约为第4代移动通信基站密度的4~5倍),且单站能耗更高(超过第4代移动通信基站3倍)[1-2]。据统计,截至2020年年底,中国已建成第5代移动通信基站超130万个,基站能耗占整体通信网络功耗的70%,并预计2025年的用电量将达到近2000亿kW·h,占全国总用电量的2%[3]。为此,如何在满足不断增长的业务需求的同时,减少蜂窝网络基站的用电成本已成为第5代移动通信网络发展亟待解决的问题。
随着能量收集(Energy Harvesting,EH)和储能技术的快速发展,在无线通信系统中,网络运营商通过为基站配备可再生能源收集装置和储能设备降低购电成本成为可能[4]。通过利用太阳能、风能等可再生能源满足基站的部分能量需求,可以减少甚至替代从电网购买的能量[5]。但随着可再生能源渗透率的提升,其出力的间歇性造成的影响不可忽视,可能影响电力系统的稳定性及能源的消纳,引入分布式储能技术配合可再生能源使用,能够平滑可再生能源出力的波动性[6-7]。文献[8]针对具有能量收集功能的基站,提出了一种基于李雅谱诺夫(Lyapunov)框架的在线算法以优化视频质量和能源消耗。文献[9]研究了蜂窝网络在高流量的情况下利用可再生能源来降低电网负荷,从而降低碳排放的问题,并使可再生能源占比高的基站服务更多的用户。文献[10]研究了单基站的最佳休眠策略,将考虑了切换能耗和延迟性能等关键因素的基站最佳休眠问题,表述为一个部分可观测的马尔科夫决策过程,通过基站休眠降低通信系统的能耗。上述研究只针对单个基站进行能量管理,并未考虑多个基站间的能量共享对购电成本的影响;同时也未考虑将储能接入电网参与电网互动发挥其调度潜力。
近年来,能量共享技术得到了大量的关注。能量共享是解决基站的可再生能源出力和移动通信能耗不完全匹配的关键技术,进一步提高了可再生能源的利用率。文献[11-12]通过部署额外的物理/专用电力线路基础设施,以适应能量共享的拓扑链路。但对于地理距离较远的大量基站,这种方法可能过于昂贵,无法在实际中应用。文献[13-14]中通过智能电网中的聚合器来协调一组基站之间共享的能量流,即一些基站向聚合器注入能量,而另一些基站从聚合器中获取能量,从而实现能量共享。然而,其参与共享的基站群未配置储能装置,可能会造成能量的浪费。文献[15]利用可再生能源和基站的动态休眠来最小化能量消耗,并将非确定性多项式(Non-deterministic Polynomial,NP)困难的混合整数线性规划问题分解为两个子问题求解,有效地降低了系统的能耗。上述研究是在基站的能量需求、可再生能源出力等参数预先知道(或准确预测)的前提下制定能量共享策略。然而,在实际情况中,基站的能量需求、可再生能源出力具有随机性,因受各种因素的影响很难准确预测。
基于上述背景,文中建立了在不确定环境下(电网实时电价、可再生能源出力、能量需求统计分布信息未知),基站间通过智能电网基础设施进行能量共享的调度模型,提出了一种基于李雅谱诺夫优化理论的能量共享实时调度算法,目标是最小化网络运营商的长期购电成本。通过理论分析,证明了所提算法在不需要知道电网电价、可再生能源出力、各基站能量需求的统计特性的情况下,优化结果(长期购电成本)无限渐近最优解(具有完整信息解决方案的最优解)。仿真结果表明,所提算法可以有效地减少网络运营商的购电成本,验证了其有效性。
2 建模和问题描述
文中研究的基站能量共享调度模型如图1所示。该模型中的多个基站隶属于同一个运营商,每个基站都配备了储能设备和能量捕获装置(如太阳能光伏板和风力发电装置),并与智能电网相连,各基站通过聚合器实现能量共享。任意基站的电能供应主要来自于4个方面:能量捕获装置收集到的可再生能源的能量、储能设备中的能量、其他基站共享进来的能量以及从智能电网购买的能量。每个基站首先由可再生能源供能,供能不足的情况下可由储能设备中的能量以及从其他基站共享进来的能量供能,最后才考虑从智能电网购买能量以满足其能量需求。基站间只共享多余的可再生能源,此外,基站通过智能电表与外部电网保持实时通信,获取电价相关信息。基站的能量管理单元(Energy Manegement Unit,EMU)可以采集基站电力需求、可再生能源发电量、储能设备能量及实时电价等相关信息,同时可以根据实时电价和各基站能量需求的时延容忍,实时优化分配能量(需求调度、存储控制及从智能电网购买的电量),在满足柔性能量需求的同时,最小化网络运营商的长期购电成本。
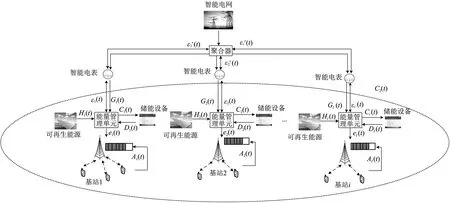
图1 基站能量共享调度模型
假设该模型由I个基站组成,并考虑T个时间段。令ω表示基站的集合,ξ表示时间段集合,即ω={1,2,…,I},ξ={1,2,…,T};i(i∈ω)和t(t∈ξ)分别为基站和时间段的编号索引。
2.1 基站的能量需求队列模型
文中考虑基站的能量需求为柔性需求,比如基站消耗的能量用于传输文件数据,只要在一定时间内满足用户需求就好。对于柔性需求可以经过一定的延时Ti后满足,以此换取更低电价的能量,以达到降低网络运营商购电成本的目标。假设t时隙基站i的能量需求为Ai(t),将其存放在能量需求队列中Qi(t),能量管理单元在时隙t供给基站i的能量为ei(t),则能量需求队列Qi(t)根据以下公式更新:
Qi(t+1)=max{Qi(t)-ei(t),0}+Ai(t) 。
(1)
2.2 储能设备模型
由于可再生能源发电出力具有间歇性和波动性,在上述模型中,基站i在时隙t收集的能量记为Hi(t)。而储能设备具有平抑收集能量的波动性的作用,不仅可以将其收集的能量进行存储,还可以参与基站的能量管理以降低网络运营商从智能电网购电的成本,例如,在低电价时从智能电网购电进行存储,供电价高且其他能量来源供给不足时使用。将基站i的储能设备在时隙t的能量记为Bi(t),在时隙t的充电量记为Ci(t),放电量记为Di(t)。储能设备在充/放电过程中具有一定的能量损耗,设储能设备的充电效率为ηch,放电效率为ηdis,则储能设备能量的更新公式为
Bi(t+1)=Bi(t)+ηchCi(t)-ηdisDi(t) 。
(2)
由于储能设备存在物理约束限制,任意时隙储能设备的充电量Ci(t)和放电量Di(t)存在上限值:
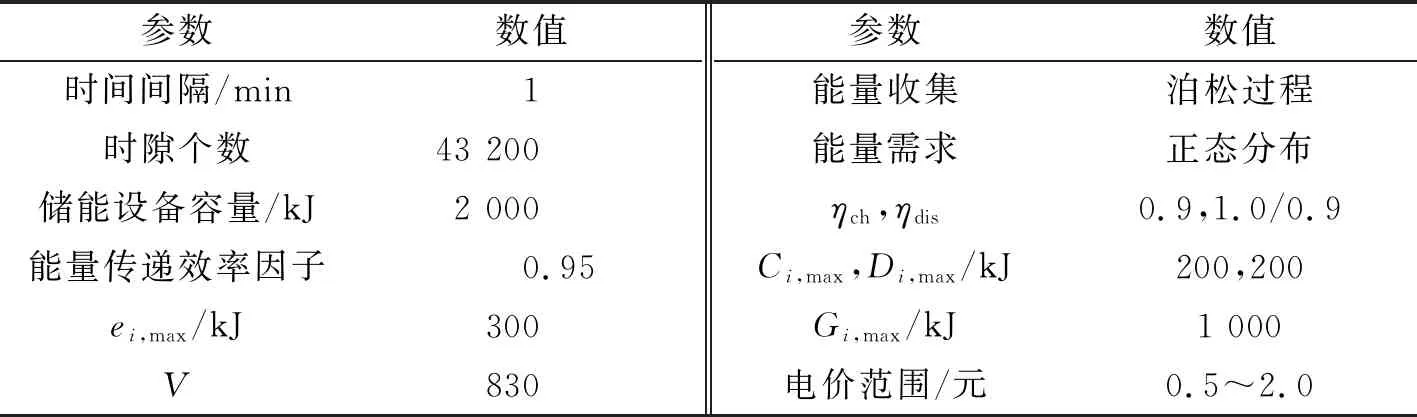
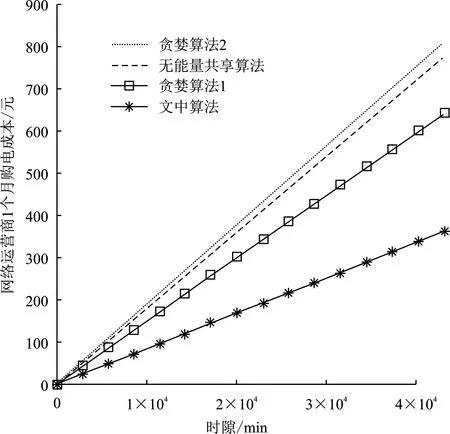
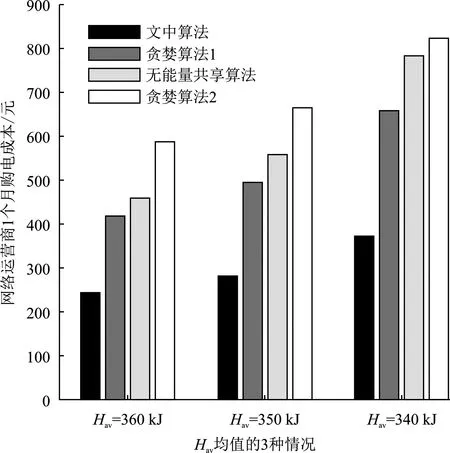
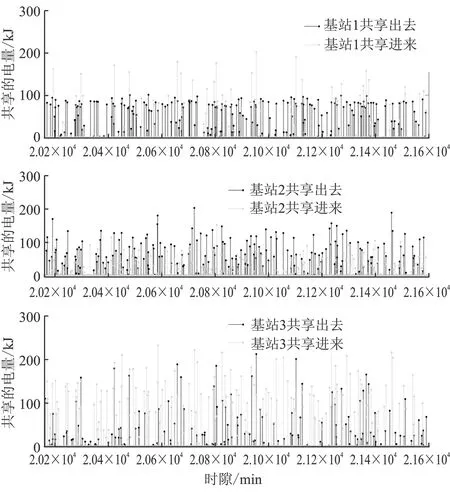
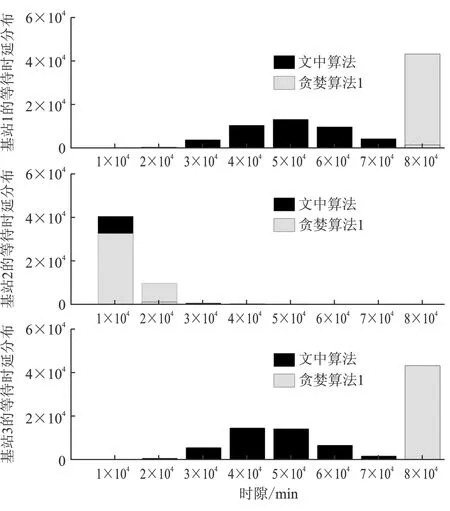
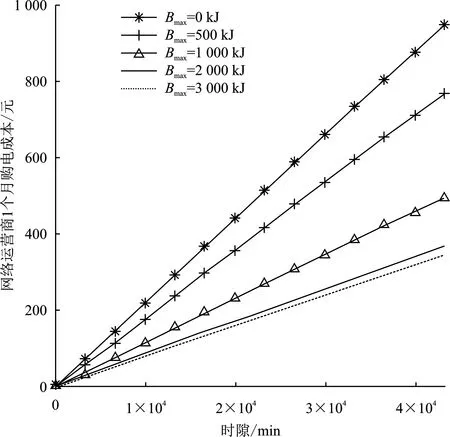
0 (3) 0 (4) 其中,Ci,max、Di,max分别表示基站i的储能设备在每个时隙充电量和放电量的上限值。 由于储能设备的存储容量有限,储能设备的容量约束为 0≤Bi(t)≤Bi,max, (5) 其中,Bi,max表示储能设备的最大容量。 为了保证储能设备正常工作,每个时隙充电和放电不能同时进行,则有 Ci(t)Di(t)=0 。 (6) 在上述基站能量共享调度模型中,聚合器允许各基站注入或抽取能量,即可再生能源盈余的基站可以通过聚合器将能量转移给可再生能量短缺的基站,从而进行能量共享。由于电力线电阻等开销,在能量传输过程中要消耗一定的能量,令β∈(0,1]表示两个基站之间的能量传递效率因子,则基站间共享的能量必须满足 (7) 其中,εi(t)表示基站i从其他基站接收的能量,ε′i(t)代表基站i转移给其他基站的能量。 为保证能量共享的正常进行,任意时隙εi(t)和ε′i(t)不能同时大于零,即 εi(t)ε′i(t)=0 。 (8) 当可再生能源、储能设备的放电量、共享进来的能量不能满足基站i的能量需求时,基站i将从智能电网购买Gi(t)的能量以满足能量短缺的部分。由基站能量共享调度模型可知,基站i的能量供需平衡关系在任意时隙t满足: ei(t)=Hi(t)+Di(t)+εi(t)+Gi(t)-ε′i(t)-Ci(t) 。 (9) 由于硬件电路的物理限制,从电网购买的能量Gi(t)满足: 0 (10) 其中,Gi,max表示任意一个时隙内从智能电网购买的能量的最大值。 (11) 0≤ei(t)≤ei,max, ∀i, (12) (13) 0≤Ti≤Ti,max, ∀i, (14) 其中,式(11)为优化目标,式中的E[·]为数学期望,通过决策最优控制策略M(t)的时间序列,使基站从智能电网长期购电的成本总和最小。其中约束式(12)中ei,max为基站i任意时隙能量管理单元可分配给基站i服务其能量需求的最大值,为保证以上问题可行,有ei,max≥Ai,max(Ai,max为任意时隙基站i能量需求的最大值);约束式(13)保证所有基站的能量需求队列保持稳定;约束式(14)中Ti表示基站i的能量需求在等待被服务期间的累计时延,累计时延不超过最大值Ti,max。 下文将引入虚拟队列解决队列的时延约束问题(即约束式(14))。 为了保证Qi(t)中所有的能量需求的等待时间都不超过最大时延,根据虚拟队列的框架[16]引入了可以感知延迟的虚拟队列Zi(t),虚拟队列更新过程为 Zi(t+1)=max{Zi(t)-ei(t)+σi1{Qi(t)>0},0} , (15) 其中,1{Qi(t)>0}为一个指示变量,当Qi(t)>0时,则其取值为1,否则取值为0。σi为一个固定的正常数,是对虚拟队列积压的惩罚,用于调节虚拟队列Zi(t)的增长速度,在实队列Qi(t)非空的情况下,虚拟队列Zi(t)在时隙t到达σi,而虚拟队列和实队列的服务速率相同(都为ei(t)),因此可以保证如果实队列Qi(t)中有未被服务的能量需求,Zi(t)就会增长。基站的能量管理单元控制队列Qi(t)和Zi(t)均保持稳定,即可确保基站i所有的能量需求都在延迟容忍期限内被服务,其最大时延不超过Ti,max个时隙,即满足约束式(14)。以下引理给出Ti,max的值。 引理1假设可以通过控制参数以确保在所有时隙t上有Zi(t)≤Zi,max和Qi(t)≤Qi,max,其中Zi,max和Qi,max是正常数,那么基站i能量需求队列的最大时延为 (16) 引理1的证明可参考李雅谱诺夫优化理论[16]。 直接利用李雅谱诺夫优化方法求解以上问题,不能保证约束式(5)。为满足目标函数中的约束式(5),即0 (17) (18) 其中,V为非负控制参数,通过合理调节参数V来控制变量Xi(t),以满足约束条件(5)。 由储能设备的能量更新公式(2)可得出Xi(t)的更新方程为 Xi(t+1)=Xi(t)+ηchCi(t)-ηdisDi(t) 。 (19) (20) 可知,当L(Φ(t))较小时,所有队列的积压较小,即队列稳定性较好。反之,至少有一个队列积压较大,队列稳定性差。为了保证Φ(t)的稳定性,引入李雅普诺夫漂移函数ΔL(Φ(t)),表示李雅谱诺夫函数从时隙t到时隙t+1的积压程度差: (21) 由上式可知,若在每个时隙t都做出相应的控制策略M(t)将ΔL(Φ(t))推向最小,则队列积压将被推向更低的值,直观上看队列运行稳定,即可保证约束式(5)、式(13)和式(14)。我们的目标是满足约束的基础上最小化优化目标式(11),因此根据李雅谱诺夫优化框架定义一个李雅谱诺夫“漂移加惩罚”函数,同时求解李雅谱诺夫“漂移加惩罚”函数的最小值,其表达式为 (22) 其中,第1项ΔL(Φ(t))为李雅谱诺夫“漂移”,表示队列积压的程度,第2项为李雅谱诺夫“惩罚”,即优化目标,表示性能。式中V是一个正数,用于调节第1项和第2项在整个优化中所占的比重,即积压-成本折中调节参数。 引理2在每个时隙t,李雅谱诺夫“漂移加惩罚”函数的边界为 (23) 其中, (24) 引理2的证明可参考李雅谱诺夫优化理论[16]。 根据李雅谱诺夫理论框架,将待求解的问题转化为最小化每个时隙的“漂移加惩罚”,该表达式有界,从而等效于最小化每个时隙的不等式(23)右边的各项。除去与决策矢量M(t)的无关项,并进一步转化为 (25) 将能量供需平衡关系式(9)代入式(25)并除去与决策矢量M(t)的无关项,可将上述能量调度管理问题求解转化为 (26) 最小化式(26),决策出时隙t能量调度管理问题的最优决策M(t)的能量共享实时调度算法如算法1所示。 算法1能量共享实时调度算法。 ① 初始化系统参数V、T、β、εi,max、ε′i,max、Bi(1)、Qi(1)、Zi(1)、Xi(1)、Bi,max、Ci,max、Di,max及初始成本C=0 ② 检测系统当前状态(Bi(t),Hi(t),P(t),Qi(t),Zi(t),Xi(t)) ③ 求解式(26),得到最优决策M(t)=[e(t),ε(t),ε′(t),C(t),D(t),G(t)] ④ 更新网络运营商累计购电成本:C=C+P(t)G(t) ⑤ 根据式(1)更新能量队列Qi(t+1);根据式(15)更新虚拟队列Zi(t+1);根据式(2)更新电池能量队列Bi(t);根据式(17)更新储能设备虚拟队列Xi(t) ⑥ 更新t=t+1,跳至②,重复执行 可见文中基于李雅谱诺夫优化理论提出的能量共享实时调度算法,最优决策M(t)只与每时隙检测的当前系统状态(Bi(t),Hi(t),P(t),Qi(t),Zi(t),Xi(t))有关,且不依赖于可再生能源出力、电网时变电价及基站的能量需求的统计特性,算法复杂度与时隙个数T呈线性关系,复杂度为O(T),复杂度低,容易实现,具有普适性。接下来将分别从理论和仿真两个方面进行证明和验证所提算法的性能。 定理1在时隙t∈{1,2,3,…,T},任意常数V满足0≤V≤Vi,max,∀i,有 (27) 其中,Pmax为最大电价,Pmin为最小电价。则上述算法具有以下性质: (1) 在所有的时隙,队列Qi(t)和Zi(t)都有上确界: Qi(t)≤VPmax+Ai,max, (28) Zi(t)≤VPmax+σi, (29) Qi(t)+Zi(t)≤VPmax+Ai,max+σi。 (30) (2) 基站i的能量需求队列中任何能量需求的最大时延Ti,max为 (31) (3) 队列Xi(t)有上下界,即 -VPmax/ηch-ηdisDi,max≤Xi(t)≤Bi,max-VPmax/ηch-ηdisDi,max。 (32) 由Xi(t)范围即可得到储能设备的能量约束: 0≤Bi(t)≤Bi,max。 (4) 假设Hi(t),Ai(t),P(t)在时隙上是独立同分布的,且σi≤E{Ai(t)},则在所提算法下的网络运营商从智能电网的平均期望购电成本与最优解Copt的差不超过F/V,即 (33) 其中,Copt为已知随机过程Hi(t),Ai(t),P(t)先验知识前提下优化目标的最优解,F的值已由上文式(24)给出。 定理1的证明可参考李雅谱诺夫优化理论[16]。 从定理1性质(1)可知,在文中的能量共享实时调度算法中,队列Qi(t)、Zi(t)在任意时隙都有上确界,这保证了队列稳定性约束;性质(2)和(4)表明能量需求等待时延Ti,max随参数V的增大而增大,而从电网的购电总成本(目标函数)随参数V的增大无限渐进最优值Copt。所提算法在不需要随机过程先验知识的条件下通过调节参数V可使目标函数的值接近最优值。性质(3)表明了充电决策Ci(t)和放电决策Di(t)的合理性,使得储能设备的能量始终保持在合理水平,即 0≤Bi(t)≤Bi,max。 文中基于主频3.30 GHz、CPU i5-6600(4核)、RAM 8 GB的Windows PC机的Matlab平台验证所提出的算法的性能,并根据市场调研相关参数设置如表1所示。从前面的分析可以看出,所提算法不依赖于随机过程的概率分布。为了方便演示,假设基站的能量需求满足正态分布,可再生能源出力满足泊松分布,对于其他统计分布,该算法也同样适用。文中考虑的基站能量共享调度模型内有3个基站,即I=3,时隙间隔取1 min,一天共划分为1 440个时隙,调度周期为30 d,即T=43 200。 表1 参数设置 为了验证所提算法的有效性,将所提算法和两种贪婪算法,以及无能量共享算法进行比较。贪婪算法1是指各基站在指定时延容忍期限内只消耗可再生能源和从其他基站共享过来的能量,若直到最后期限仍未满足该时隙的能量需求,才从智能电网购买能量,这里最大期限为8个时隙;贪婪算法2是指各基站的能量需求立即被满足,若可再生能源和共享的能量不能满足要求,立即从智能电网购买能量。无能量共享的场景中,基站间不能共享收集的可再生能源。图2为4种算法下网运营商1个月的累计购电成本。由图2可计算出,基于所提算法网络运营商的购电成本约为367.58元,其购电成本最低;相比于贪婪算法1(约645.92元)、无能量共享算法(约779.35元)及贪婪算法2(约817.26)分别降低了约43.1%、52.8%、55.0%。所提算法之所以优于其他几种算法,原因是:所提算法不仅综合考虑各个基站的情况,允许基站间共享多余的可再生能源,提高了可再生能源的利用率;而且在满足基站能量需求的同时,合理利用储能设备的充放电过程,在低电价时从智能电网购电进行存储供电价高且其他能量来源供给不足时使用,利用电价差获取一定的收益。 图2 文中算法与其他方法对比 由于可再生能源出力具有不可控性和随机性,为了充分验证文中算法的普适性(即不受分布式可再生能源出力的影响),在可再生能源出力均值Hav分别为360 kJ,350 kJ,340 kJ的3种情况进行仿真验证。仿真结果如图3所示。由图3可见:①可再生能源发电量越多,可用的免费能量越多,网络运营商的购电成本越低;②无论可再生能源出力均值处于什么水平,基于所提算法网络运营商的购电成本均比其余两种算法低。因此可得所提算法具有较好地普适性,不依赖于可再生能源出力的概率分布,能够较好地解决随机环境下的基站间的能量共享调度问题。 图3 可再生能源3种情况各个算法的购电成本 图4给出了第15天3个基站能量共享的情况。由图4可计算出,基站1、基站2、基站3分别约有277、401、322个时隙进行能量共享,分别占一天的总时隙的约19.2%、27.8%、22.4%。基站间进行能量共享可以提高可再生能源的利用率,从而减少基站从智能电网的购电量,节约成本。 为了评估提出的算法在时延方面的性能,图5给出了在文中算法和贪婪算法1下的3个基站能量需求时延分布情况。可以看出,在文中算法下3个基站能量需求时延等待均小于贪婪算法,其中基站1和基站3的能量需求等待时延要远小于贪婪算法,对于基站2时延性能表现不明显,这是因为基站2的可再生能源相对较多,可以相对及时地满足能量需求。 为了评估储能设备容量Bmax对所提算法的影响,图6给出了网络运营商在不同储能设备容量下的购电成本,图中针对不同的Bmax,选取了合理的调节参数。由图6可见,Bmax越大,基站的成本越低。这是因为Bmax越大时,存储的可再生能源及从智能电网购买的低价电能就越多,以备日后电价较高时使用,从而节约成本。但基站的成本并不随着储能设备的容量的增大而线性地减小,这是因为储能设备的最大充/放电速率有限,即使储能设备的容量很大,但单位时间内储能设备无法存入或放出更多的能量。 图7为不同控制参数V对平均等待时延和购电成本的影响。由图7可见,能量需求队列的平均时延随着V的增大而增大,而购电成本随着V的增大而减小,这与理论分析中的结论一致(式(31)和式(33))。但当V值到达某个比较大的值时(V≈2 500),平均等待时延和购电成本的变化较小(趋于饱和)。当V≈830时,在总成本与平均时延之间的权衡最大。这是因为V≈830是一个合理的数值,可以达到较低的平均时延。在满足基站的能量需求在合适时间内被服务的同时,保证总购电成本趋于我们所提算法的最优值。 图4 第15天3个基站能量共享的情况 图5 文中算法与贪婪算法1的延迟比较 图6 不同储能设备容量下基于所提算法的购电成本 针对具有可再生能源收集装置和储能设备的第5代移动通信基站间能量共享调度问题,基于李雅谱诺夫优化方法设计了一种低复杂度的能量共享实时调度算法,基于所提算法可使得网络运营商的长期购电成本最小,同时可保证基站柔性能量需求不超过最大时延。该算法的优势是不依赖智能电网电价实时波动、基站的能量需求以及可再生能源出力的统计分布。理论分析证明了该算法可使网络运营商的购电成本无限接近最优值,最后通过仿真验证了该算法的有效性。仿真结果表明,所提能量调度管理策略在降低网络运营商购电成本的同时,显著降低了能量需求的等待时延,并且在服务时延上优于基准的贪婪算法。此外,通过分析不同参数对所提算法的影响,为第5代移动通信网络运营商如何选取合理的参数提供参考依据。2.3 能量共享及供需模型

3 问题规划及求解
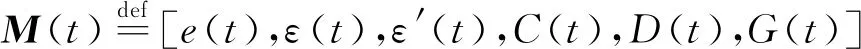

3.1 时延约束保证
3.2 基于李雅谱诺夫优化方法的策略
3.3 能量共享实时调度算法
4 算法性能理论分析
5 仿真验证
6 结束语
