一种电流模式Buck-Boost变换器的混沌与反混沌混合控制方法
2023-11-17龚仁喜彭维玉李思强
龚仁喜,彭维玉,李思强
(广西大学 电气工程学院,南宁 530004)
0 引 言
典型PWM控制的开关变换器属于强非线性系统,在某些电路参数条件下会表现出丰富的非线性行为,如倍周期分岔[1-2]、边界碰撞分岔[3-4]、Hopf分岔[5]和混沌行为[6-7]等。研究者最初致力于抑制或消除这些非线性现象,即变换器的混沌控制。随着研究的不断深入,人们发现混沌并非完全有害。如可以根据混沌连续频谱的特性,采用混沌PWM抑制变换器的EMI[8-9];利用混沌的初值敏感性,提高变换器的增益[10]。基于此,对各类变换器分岔和混沌特性的研究,可从一个新的视野认识其运行机制,对与提高变换器的性能具有重大的实际意义。
为了深刻认识变换器的这些非线性行为的产生机制并实施有效控制,国内外已有学者对此进行了研究,并提出了一些混沌和反混沌控制方法。混沌控制方法,如延迟反馈法[11]、微分反馈法[12]、指数延迟反馈[13]等,主要通过改变外部输入或内部参数等使原处于混沌状态的系统重回周期轨道。但这些方法会引起变换器性能的改变,不利于工程运用。反混沌控制方法,如时间延迟反馈法[14]、自适应滑模控制法[15]等。主要通过调节系统的控制参数或外加补偿的方法,将稳定状态的变换器控制至混沌状态,使得EMI能量分布在比较宽的工作频带上,达到降低电磁辐射峰值的目的,并最终有效抑制EMI。但这些方法在数学上进行分析时比较困难,缺乏严谨的理论证明。文献[16]基于状态关联对电流型Boost变换器实现了混沌与反混沌的控制,取得了较好的控制效果。但该方法运用到电流型Buck-Boost变换器中不能让变换器从混沌态重回周期1期态,混沌控制效果不好。迄今为止,采用相应的控制方法同时实现对其混沌控制和反混沌控制尚未见报道,且提出的变换器混沌化控制方法,大都缺乏严谨的理论依据,在数学意义上不能严格解释系统混沌化控制机理,导致它们的实际应用受到限制[17-20]。
为解决上述存在的问题,本文首先分析了变换器的参考电流发生变化时系统表现出的不稳定。为实现该变换器的混沌与反混沌控制,基于参数扰动和状态关联的思想提出了一种混合控制方法。该方法首先定义一个调整系数来表征状态变量之间的耦合强度,通过调节该系数达到控制其耦合强度的目的,并建立系统的数学模型。然后根据混沌系统对参数变化具有高度的敏感特性,利用系统的微分项来构造参数扰动项,对混沌系统进行一定范围的参数扰动。最后根据系统所处的状态和控制目标的需要,通过改变调整系数实现对系统的混沌与反混沌控制。利用单值矩阵理论验证了该方法的混沌与反混沌控制的可行性,同时在Simulink中建立系统的仿真模型,通过相图、电感电流波形图、输出电压波形图以及频谱图验证了方法有效性。同时也表明仅需调整一个外部参数,即可将任意状态下电流型Buck-Boost变换器控制在周期1、周期2轨道以及混沌态。
1 新型混合控制方法
考虑一个二维的混沌系统:
(1)
式中x1、x2为系统的状态变量。
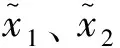
(2)
式中h称为调整系数,表示x1与x2之间的关联性或耦合强度,h的取值范围为h∈(-1,1)。
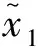
(3)

(4)
对于不同h的取值有以下不等式成立:
h(1-h)(x12+x22)<2h(1-h)x1x2,h<0
(5)
h(1-h)(x12+x22)>2h(1-h)x1x2,h>0
(6)
由式(4)~式(6)可知:
(7)
(8)
因此,由式(7)、式(8)可知h是具有实际物理意义的。当h∈(-1,0)时,表示两个状态变量x1和x2之间为负相关,表现为当x1上升时,则x2下降。当h∈(0,1)时,表示x1和x2为正相关,即x1上升x2也会上升。
由于混沌系统对参数具有很强的敏感性,若混沌系统的参数被另一组混沌序列持续扰动时,系统将产生更加难以预测的混沌现象。为此,本文通过利用系统的微分项构造参数扰动项对系统进行扰动,同时为保证控制更容易实现,减少外部可调参数,选取的扰动强度系数与耦合强度在数值上相同,得到控制后的混合控制系统为:
(9)

(10)
当h=0时,式(10)退化为式(1)。当-1 典型的脉宽调制(PWM)型电流控制型Buck-Boost变换器原理图如图1所示。主电路由开关S、二极管D1、电感L、电容C、电源E和负载电阻R等组成。控制电路由一个比较器和一个RS触发器构成。 图1 电流型Buck-Boost变换器 选取系统的状态变量x=[iL,uC]T,其中iL为电感电流,uC为电容电压。根据变换器中功率开关的工作状态和基尔霍夫定律,可建立系统受控前的分段线性模型: (11) (12) 由此可获得变换器的状态矩阵如表1所示。 表1 Buck-Boost变换器数学模型 对于电流型连续导电模式(CCM)Buck-Boost变换器,当iL上升到参考电流Iref时,开关管S由导通转为关断,则切换信号的表达式为: h1=iL-Iref=0 (13) iL和uC为变换器的两个状态变量,即有x1=iL,x2=uC。给变换器施加控制方法后,系统的状态矩阵如表2所示。 表2 混合控制的Buck-Boost变换器数学模型 对于电流型CCM模式下的Buck-Boost变换器,当S导通时,D1截止,变换器的状态方程可表示为: (14) 当D1导通时,S截止,变换器的状态方程变为: (15) 其中: 又有: nT=[1,0] (16) (17) (18) (19) (20) 同时单值矩阵的表达式为: (21) 对具有两个子系统的开关变换器,开关点的迭代方程可表示为: (22) (23) 联立式(22)、式(23),并基于牛顿-拉夫逊方法解该方程组可以得到系统状态发生改变时变量x和占空比d的具体值。 将占空比d和切换点状态变量x的具体值代入式(21),可得M的表达式并求其特征根,此时便可知M的Floquet乘子。而单值矩阵的本质就是将系统的周期轨道在平衡点处线性化,求得其最大的特征乘子,即Floquet乘子。若Floquet乘子处在单位圆内,系统是稳定的,反之,系统变得不稳定。 为研究实施控制前系统的非线性行为,本文采用的参数如下:Iref=0.5~4 A,L=0.5 mH,R=10 Ω,C=4 μF,T=50 μs,E=8 V。 当h=0时,此时为未施加控制方法的原系统,其中uC随参考电流Iref变化的分岔图如图2所示。 图2 电容电压uC随Iref增大的分岔图 由图可以看出,uC随Iref的增大发生了倍周期分岔最后进入混沌态。 为预测系统分岔处的类型,令Floquet等于1,即: max|λM|=1 (24) 由式(22)、式(23)可以得到切换点的状态变量x,再联立式(21)、式(24)可得Iref=1.753 8 A。此时λM的两个特征值分别为-1.000和0.842 5,随着Iref的增大,系统的两个特征根一个将从负半轴穿过单位圆,而另外一个仍然处在单位圆内,这时系统将发生倍周期分岔,这与图2所示的结果是一致的。 当Iref=3.5 A时,h∈[-0.3,0]范围内电容电压uC随h的变化如图3所示,给定Iref和调整h时计算得到的单值矩阵特征根,结果如表3所示。 表3 混沌控制Floquet乘子和系统状态 图3 Iref=3.5时,uc、h分岔图 由图3及表3可以看出,当h=0时,系统处于混沌态,随着h的减小系统从混沌态过度到倍周期态,周期1态,扩展了系统的稳定边界。但图3中出现了不连续现象,这是因为随着h的不断减小在h∈(-0.181 1,-0.162 1)时系统出现了稳定的周期1态态,但在h=-0.181 1附近系统发生倍周期分岔进入到了周期2态,然后随着h的继续减小再次进入到稳定的周期1态。同时基于Simulink仿真平台搭建了系统的仿真模型,得到其对应的电感电流、电容电压、电容电压和电感电流的相图如图4~图8所示。 图4 Iref=3.5 A,h=0时,电容电压、电感电流波形图以及相图 1)从图4(a)、(b)所示的电感电流、电容电压以及相应的相图可以看出:Iref=3.5 A,h=0时,系统处于混沌态; 2)从图5和图6(a)、(b)所示的电感电流、电容电压以及相应的相图可以看出:Iref=3.5 A,h=-0.21和h=-0.19时,原混沌系统被控制在周期2状态; 图5 Iref=3.5 A,h=-0.21时,周期2电容电压、电感电流波以及相图 图6 Iref=3.5 A,h=-0.19时,周期2电容电压、电感电流波形图以及相图 3)从图7、图8(a)、(b)所示的电感电流、电容电压以及相应的相图相图可以看出:Iref=3.5 A,h=-0.3和h=-0.25时,原混沌系统被控制在周期1状态。 图7 Iref=3.5 A,h=-0.3时,周期1电容电压、电感电流波形图以及相图 图8 Iref=3.5A,h=-0.25时,周期1电容电压、电感电流波形图以及相图 从图4~图8可以看出,当h从零开始不断减小时,该控制方法能将系统从混沌态控制到周期1、周期2态,实现对系统的混沌控制,扩展系统的稳定边界,改善了系统的性能。 由3.1节分析可知,当Iref<1.753 8 A时,系统处于稳定的周期1状态。图9给出了当h∈[0,0.2],Iref=1.5 A时电容电压随h变化的分岔图。表4示出了给定Iref和调整h时计算得到的单值矩阵的特征根。 表4 反混沌控制Floquet乘子和系统状态 图9 Iref=1.5 A时,uC-h分岔图 由图9及表4可以看出,取Iref=1.5 A,当h=0时,系统处于周期1态,随着h的逐渐增大,系统由周期1状态被反控制到倍周期态和混沌态。同时基于Simulink仿真平台搭建了系统的仿真模型,其对应的电感电流、电容电压、电容电压和电感电流的相图如图10~图12所示。 图10 Iref=1.5 A,h=0时,周期1电容电压、电感电流波形图以及相图 1)从图10(a)、(b)所示的电感电流、电容电压以及相应的相图可以看出:当Iref=1.5 A,h=0时,系统处于1周期态; 2)从图11(a)、(b)所示的电感电流、电容电压以及相应的相图可以看出:当Iref=1.5 A,h=0.06时,系统处于倍周期态; 3)从图12(a)、(b)所示的电感电流、电容电压以及相应的相图可以看出:当Iref=1.5 A,h=0.12时,系统处于混沌态。 图12 Iref=1.5 A,h=0.12时,混沌态电容电压、电感电流波形图以及相图 从图10~图12可以看出,当h由零不断增大的时候,该控制方法可以将处在周期1态的系统控制到周期2及混沌态,实现系统的反混沌控制。 图13(a)、(b)给出了Iref=1.5 A时,h=0.12和h=0的驱动PWM频谱图。 图13 混沌态与周期1态PWM频谱 从图13(a)可知,当处于混沌态时系统的驱动PWM频谱处在多个周期频段内,此时EMI被分散在各个频点,与图13(b)相比其频谱的峰值明显降低,达到了EMI抑制的效果。 本文对连续导电模式电流型Buck-Boost变换器的非线性动力学特性进行了研究,提出了一种混沌与反混沌混合控制方法。基于单值矩阵理论对系统控制性能进行了理论验证,同时搭建了系统的Simulink模型验证了方法的控制效果。研究表明该方法仅需调整一个外部参数,即可将任意状态下的这种变换器控制到周期1、周期2轨道及混沌态,且方法具有控制结构简单、适应性强、控制效果好的特点,为变换器的混沌控制与反混沌控制提供了一种新的方法。2 采用混合控制方法后Buck-Boost变换器的单值矩阵及切换点计算

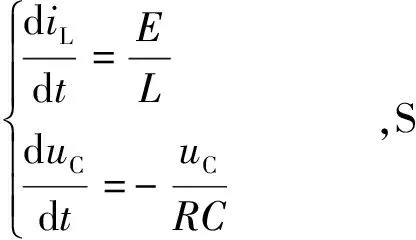


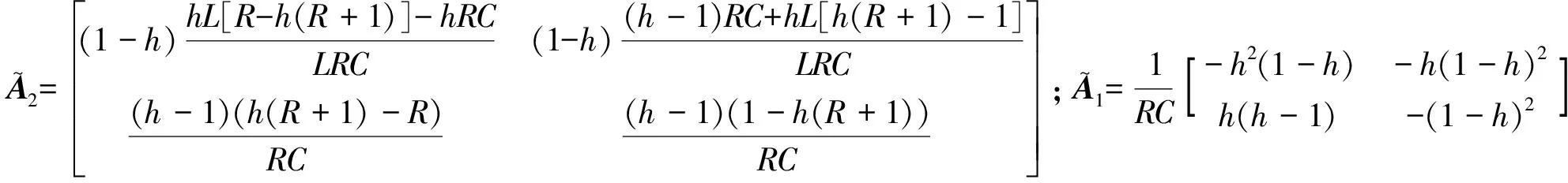



3 电流模式Buck-Boost变换器混沌与反混沌控制
3.1 控制前Buck-Boost变换器的非线性行为
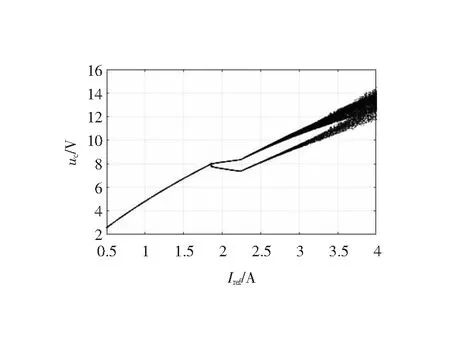
3.2 混沌控制
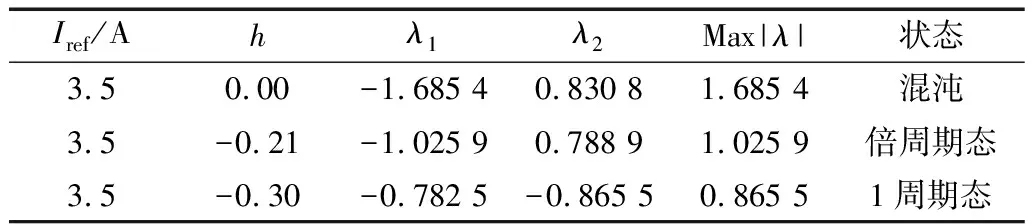
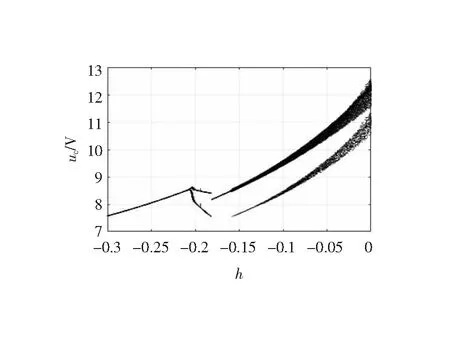
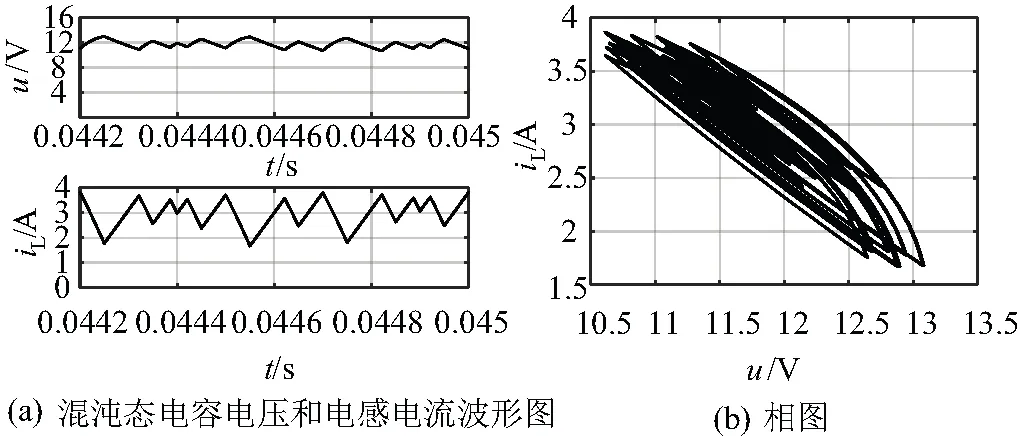



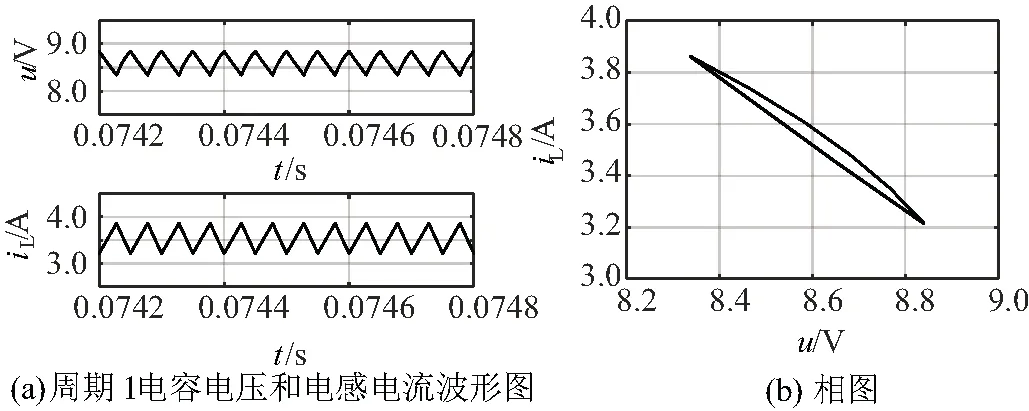
3.3 反混沌控制
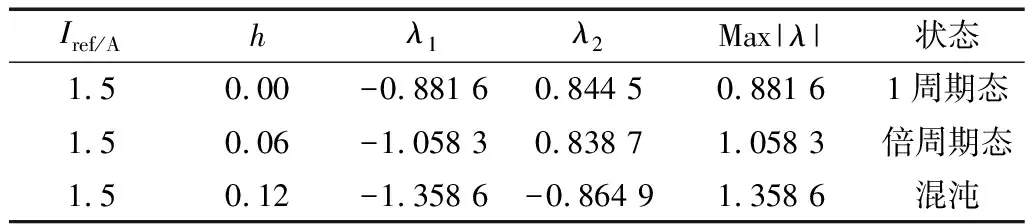



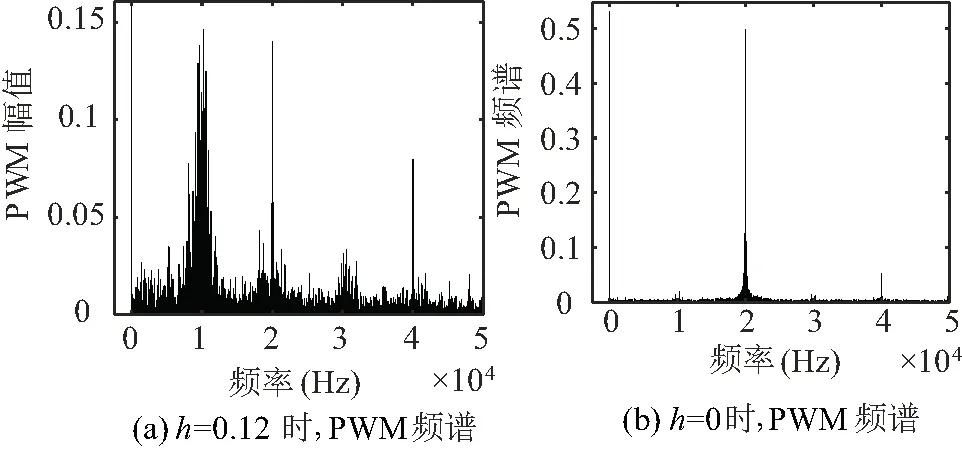
4 结束语
