基于改进粒子群算法的多能微网多目标优化调度

2023-11-17王钰郝毅王磊党旭鑫蒋立媛张育炜肖迁

电测与仪表 2023年11期

王钰,郝毅,王磊,党旭鑫,蒋立媛,张育炜,肖迁

(1.国网天津东丽供电公司,天津 300300; 2.国网天津市电力公司,天津 300010;3.天津大学电气自动化与信息工程学院,天津 300072)

0 引言

随着能源革命进入攻坚期,我国对于能源转型升级的需求愈发强烈。传统能源供应模式为单一型能源供给,在价格和政策等多方面因素影响下,容易出现能源供应不足、利用率低等问题[1-3]。与含上述单一型能源供给系统不同,多能微网作为一种新能源供应模式[4-6],可以实现各类能源的集成,提升其利用率,降低用能成本。

近年来众多学者围绕多能微网建模与优化开展了相关研究[7-9]。在建模方面,文献[10]构建了包括电锅炉、燃气内燃机等电热耦合设备在内的工业园区多能互补系统,并以综合发电成本为目标函数,建立系统经济调度模型,有效降低了其运行成本、提升了供能可靠性;文献[11]围绕热电联供设备开展研究,建立并网条件下的微网经济优化模型,探究热电联供系统的经济效益;文献[12]考虑可再生能源与负荷的不确定性,建立了多能互补系统日前优化调度模型;文献[13]建立了天然气-电力混合系统动态模型;文献[14]计及风电出力的波动性,提出一种微网热电联合调度的优化模型。上述文献虽然利用能源耦合设备实现了系统的优化运行,但是系统内部能源耦合种类较少且荷侧类型单一,无法应对多种负荷需求下的稳定运行工况。

在优化调度方面,文献[15]以综合成本最低为目标,实现了考虑热动态和碳交易的电-气-热微网系统协调优化调度;文献[16]以最小投资和运行成本为目标,对包含风力发电、光伏发电、电池储能和柴油发电机的系统进行容量优化设计;文献[17]以多能系统接入主动配电网为背景,建立了考虑调度成本与负荷曲线方差的主动配电网多源多目标协调优化调度模型,并利用PSO算法对模型进行求解;文献[18]为减小电网负荷峰谷差、降低火电调峰成本、减少弃风量,建立了光热-风电联合系统的电网调度模型,并利用PSO算法求解优化问题。上述文献的研究重点集中于多目标优化模型的建立与求解,采用传统PSO算法求解多目标优化模型容易产生收敛困难、速度较慢等问题,难以满足系统的实时调度需求。

针对上述问题,文中提出了一种基于改进PSO算法的多能微网多目标优化调度方法。该方法充分考虑微网的运行成本与环境成本,建立其多目标优化调度模型,降低系统综合成本;改进PSO算法通过优化惯性参数与学习因子的迭代过程,并采用自适应粒子寻优策略,加快收敛速度。最后,设置多场景算例进行对比分析可知:与传统方法相比,所提基于改进PSO算法的多目标优化调度方法能够有效提升算法收敛速度、降低系统综合成本,兼顾其运行经济性与环境友好性。

1 多能微网模型

文中为实现多能微网的多目标优化运行,需要建立系统中各能源耦合关系模型与设备数学模型,并分析能源间耦合机理。

1.1 多能微网模型

图1为多能微网模型,系统中的供能设备主要包括光伏发电机组(photovoltaic generator,PV)、风力发电机组(wind turbine generator,WTG)、微型燃气轮机(micro gas turbine,MGT)、燃气锅炉(gas boiler,GB)、热泵(heat pump,HP)、余热锅炉(heat recovery steam boiler,HRB)、电制冷机(electric refrigerator,ER)与吸收式制冷机(absorption,refrigerator,AR),储能设备主要包括储电系统(energy storage system,ESS)、储热系统(heat energy storage system,HSS)、储冷系统(cooling energy storage system,CSS),上级网络主要包括电网与气网,负荷主要包括电负荷、热负荷与冷负荷。

1.2 多能微网能源耦合机理分析

多能微网打破了不同能源间相对独立的格局,通过集成PV、WTG、GB等多类型供能设备,形成一个多能源综合供给系统[19],满足各类负荷需求。在图1所示的微网模型中,电能供应设备主要包含PV、WTG与MGT,其中MGT通过消耗气能为负荷供电,实现电-气间的耦合;热能供应设备主要包含GB、HP与HRB,其中GB与HP分别实现系统的气-热耦合与电-热耦合,HRB则通过吸收MGT产生的热能,提升能源利用率;冷能供应设备主要包含ER与AR,其中ER耗电产冷,实现电-冷耦合,AR则耗热产冷,实现热-冷耦合;各类型储能可实现不同能源的削峰填谷,平抑可再生能源波动,保证系统的可靠运行。相较于传统单一供应电能的微网,多能微网能够有效提高各类能源的利用率,满足用户多种用能需求。

1.3 多能微网设备数学模型

文中将多能微网中的设备分为供能与储能两类,分别对其进行数学建模。

1.3.1 供能类设备建模

1)电能供应设备。

(a)PV与WTG。

在多能微网中,用电负荷可通过系统内的PV与WTG获取电能。文中以二者预测功率为输出功率的最大值,数学模型分别如下:

(1)

(2)

(b)MGT。

MGT通过消耗气网中的天然气进行燃烧发电,其耗气产电模型如下:

(3)

(4)

(5)

2)热能供应设备。

(a)GB。

GB通过消耗天然气进行燃烧产热,实现对系统热能的供应,GB耗气产热模型如下:

(6)

(7)

(b)HP。

HP通过消耗电能输出热能,实现电、热能源的转换。其数学模型如下:

(8)

(9)

(c)HRB。

HRB通过对MGT在发电过程中产生的热量进行回收,产热模型如下:

(10)

(11)

3)冷能供应设备。

(a)ER。

ER通过消耗电能为系统提供冷功率,其数学模型如下:

(12)

(13)

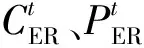
(b)AR。

AR通过吸收热能为系统提供冷功率,其数学模型如下:

(14)

(15)

1.3.2 储能类设备建模

1)ESS。

文中多能微网采用的ESS需满足充放电功率约束与荷电状态(State of Charge,SOC)约束,其数学模型如下:

(16)

(17)

(18)

(19)

式中,T为调度时间。

2)HSS。

HSS可在系统中热功率盈余时存储热能,在系统中热功率缺乏时释放热能,弥补功率缺额。其数学模型如下:

(20)

(21)

3)CSS。

CSS的数学模型如下:

(22)

(23)

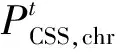
2 多能微网多目标优化调度模型

文中在构建多能微网多目标优化调度模型过程中,充分考虑系统运行经济性与环境友好性,制定各类设备的最优出力计划。

2.1 目标函数

为保证多能微网的运行经济性与环境友好性,本节选择系统运行成本与环境成本作为目标函数,其中环境成本即为碳排放成本。两目标函数具体描述如下:

(24)

式中,Ce,grid、Cgas,grid与Ceq分别为系统与电网交换电功率产生的成本、与气网交换气功率产生的成本、储能类设备老化成本;Ccar为碳排放成本。接下来将分别介绍各成本的具体数学模型。

1)与电网交换电功率产生的成本Ce,grid。

(25)

2)与气网交换气功率产生的成本Cgas,grid。

(26)

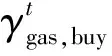
3)储能类设备老化成本Ceq。

(27)

4)碳排放成本Ccar。

(29)

2.2 约束条件

多能微网多目标优化调度模型除考虑1.3节中各类型设备的运行约束外,还需要满足电、气、热、冷平衡约束。

1)电平衡约束。

(30)

2)气平衡约束。

(31)

3)热平衡约束。

(32)

4)冷平衡约束。

(33)

3 改进PSO算法

PSO算法是一种利用随机法求取多维函数特定区域最值的算法,具体可描述如下:在D维空间中存在m个粒子,第i个粒子的位置为一矢量xi;第i个粒子的速度为一矢量Vi;第i个粒子搜索到的最优位置为pi;整个粒子群搜索到的最优位置为pgbest;粒子速度和位置的迭代公式如下:

(34)

(35)

式中,i=1,2,3…,m;d=1,2,3…,D;ω为惯性参数;c1,c2为学习因子;r1,r2为随机数;等式右边的三项分别为历史速度记忆部分、认知部分、社会部分。

3.1 主要参数迭代过程的改进

传统PSO算法的寻优性能在很大程度上依赖于其惯性参数、学习因子的设置。初始粒子在每一次迭代过程中,当进行了空间位置、速度的更新后,往往忽略了不同代粒子间的差异性[20]。针对该问题,文中对以上参数进行约束,采用一种线性递减的参数设置方法对传统PSO算法进行改进:首先设定较大的惯性参数和学习因子,开始算法迭代;在每次迭代过程中对参数进行实时调整;最后以较小的惯性参数和学习因子结束迭代过程。此方法能够有效提升初始粒子群的全局寻优能力,并促使粒子群跳出局部最优解,参数的具体更新规则如下:

(36)

(37)

式中,ωmax、ωmin的值分别为0.9和0.7;cmax、cmin的值分别为1.5和1。

3.2 自适应粒子寻优策略

PSO算法求解过程中,搜索粒子的历史与全局最优粒子会不断更新并引导其余搜索粒子向最优位置飞行,从而达到算法收敛的效果,但搜索粒子的快速聚集会导致出现较多近距离无效解,且容易使算法落入局部最优,因此引入自适应算子设定粒子寻优策略,当粒子满足式(39)位置更新条件,即可依据式(40)进行位置变换寻优,具体策略如下:

(38)

(39)

(40)

式中,e为自适应算子;rand(·)为随机数函数;e-k/kmax为自适应阈值;Li,j为粒子i与相距最近的粒子j在目标函数构成的D维空间中的欧氏距离;Li,gbest为粒子i与种群最优粒子的欧氏距离;Q为寻优判定阈值。

算法初期初始粒子与最优粒子相距较远,Li,gbest较大,对应自适应算子e较大,粒子位置更新策略主要受自适应算子项的影响,粒子多样性得到增强;算法后期粒子逐渐靠近全局最优解,此时自适应算子项对粒子位置更新的影响较小,粒子主要依靠自身位置进行寻优,保证算法的小范围求解能力。

3.3 模糊决策

多目标PSO算法求解得到的最终结果为帕累托最优解集,为确定最终的调度方案,文中采用模糊决策方法[21],将运行成本与环境成本两个目标函数进行模糊化处理,处理函数如下:

(41)

式中,fi为第i个帕累托最优解的单目标函数值;Tari为模糊处理后的目标函数值;fmax与fmin为对应目标函数的最大值与最小值。

然后,把[运行成本,环境成本]作为因素集,并对PSO算法所得非劣解集做单因素评价,组成模糊评价矩阵。为便于分析,本文评价因素权向量取[0.5,0.5]。最后进行模糊综合评判,取最优者作为最终的调度方案。

3.4 算法流程

为验证文中所提改进PSO算法的正确性与有效性,设定改进PSO算法的求解流程和优化计算方法。首先,初始化粒子群,并根据各设备的模型需求设定对应粒子群的速度阈值与越限应对机制,进行初次计算、粒子群历史最优与全局最优位置记录;其次,在每次迭代过程中对惯性参数和学习因子进行更新,判断粒子自适应寻优条件并进行对应计算,记录迭代的帕累托最优解集;最后,在系统迭代至设定次数后停止寻优,记录此时迭代记录的历史最优值集合并输出。将上述条件转化为建模语言的形式,利用MATLAB R2021进行求解,具体求解流程图如图2所示。

图2 改进PSO算法求解流程图

4 仿真分析

文中建立了如图1所示的多能微网,设置粒子群个数为100,迭代次数为1 000次;系统内主要设备参数如表1、表2所示,分时电价如表3所示,各类能源负荷、PV与WTG出力情况如图3所示,其中各能源负荷为日前预测数据。

表1 微网供能类设备参数

表2 微网储能类设备参数

表3 分时电价

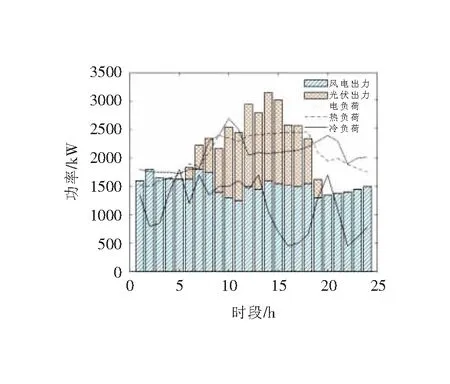
图3 风电、光伏出力及系统负荷

4.1 PSO算法优化分析

图4为利用文中所提算法求解模型所得的帕累托最优解集,由于目标函数存在冲突,无法同时达到最优解,因此只能寻求帕累托最优解,根据帕累托最优解集拟合帕累托近似前沿曲线如图所示。考虑到系统的经济性和环境友好性,分别利用传统PSO算法和改进PSO算法对建立的模型进行优化计算,由于两个目标函数模糊决策评价系数相同,在此采用相加的方式输出运行结果,两种方法的迭代收敛情况如图5所示。

图4 帕累托最优解集

图5 函数最优适应度进化曲线

由图5可知,改进PSO算法在迭代至300次左右即可达到收敛,最优适应度稳定在135.32万元,而传统PSO算法在迭代至410次左右仍存在较为明显的波动,迭代450次左右达到收敛,最优适应度稳定在142.68万元;经计算,改进PSO算法优化后的系统成本降低7.36万元。由以上分析可知,改进PSO算法相较于传统PSO算法,可以在加快模型收敛速度的同时,提升系统整体经济性。

4.2 多目标运行分析

为了验证所提多目标优化调度模型的有效性,设置了三种场景进行对比分析,不同场景下的最优调度结果如表4所示。

表4 各场景最优调度结果

1)场景1:以运行成本最小为目标求解单目标优化模型;

2)场景2:以环境成本最小为目标求解单目标优化模型;

3)场景3:以运行与环境综合成本最小为目标求解多目标优化模型。

由表4可知,场景1、2配置的单一目标函数具有一定的局限性,场景1的运行成本与场景2的环境成本分别低于场景3的对应值,这是由于多目标优化问题中各子目标是相互矛盾的,一个子目标的改善有可能会引起另一个或几个子目标的性能降低。如在售电电价较高的时刻,系统可通过MGT等机组产出电力,通过向电网售能获取额外收益,从而降低系统的运行成本,而机组的额外出力将导致排放的CO2增加,环境成本达到30.29万元,在侧重于降低系统运行成本的情况下忽视了低碳环保的需求;当采用环境成本最低进行单目标优化计算时,为降低CO2排放量,在用能需求较大的时刻,系统会向上级电网购买部分电能,此时能源价格往往较高,牺牲了一定的经济性,导致系统运行成本上升至130.68万元。因此虽然场景1相较于场景3运行成本降低1.32万元,但环境成本上升9.23万元;场景2相较于场景3环境成本降低0.49万元,运行成本却上升20.64万元。场景3综合了场景1与场景2的目标函数,在兼顾系统运行成本和环境成本的前提下获得了“次优解”,体现了多目标优化策略对多方利益的协调性。综上所述,场景3的综合成本明显低于场景1与场景2,由此验证了多目标优化调度模型可有效降低系统综合成本。

电功率多目标优化调度结果如图6所示。

图6 电负荷与设备电功率

由图6可知,系统电能消耗途径有三种,分别为电负荷、ESS设备充电以及在热负荷需求较大时刻HP生产热能所消耗的电能。在综合考虑运行成本和环境成本的情况下,系统优先使用环境成本较低的PV与WTG作为系统内主要电能供应方,MGT配合HRB实现天然气与电能、热能的转换,相较于单能源产出设备,能够较大程度降低CO2的排放量,因此在系统可再生能源供应无法满足需求时优先启动MGT机组。当微网内部电能充裕时,如6:00—7:00,可将约700 kW电能转移至ESS中,以辅助解决负荷高峰时段的电能供给不足问题;同时,系统会在电价较高时段售出一部分电能,获取收益以降低运行成本。

热功率多目标优化调度结果如图7所示,由图7可知,系统热能消耗途径有两种,包括热负荷与HSS蓄热。受MGT产电功率约束限制,HRB只能提供一定热能满足系统需求,主要的供能设备为GB与HP,其中GB作为能源耦合设备,通过消耗天然气产生的热量可经AR部分转化为冷能,因此在冷热负荷均考虑的系统中,GB会优先投入使用;当GB提供的热能无法满足需求,系统则会选择投入HP消耗电能产生热能。此外,为了降低运行成本,在热需求较低时段,系统会将额外产出的热能储存在HSS中,如6:00—7:00与15:00,分别储存了约500 kW和200 kW热能,在热负荷尖峰时刻释放热能,避免设备额外出力导致运行成本与环境成本的上升。

图7 热负荷与设备热功率

冷功率多目标优化调度结果如图8所示。

图8 冷负荷与设备冷功率

由图8可知,系统冷能消耗途径有两种,分别为冷负荷和CSS储冷。冷负荷主要由AR通过吸收热能制冷进行平衡,CSS在制冷设备出力较多时存储冷能,在AR无法满足用能需求时优先于ER投入使用。考虑到ER通过消耗电能制冷,AR的优先使用一方面可以降低ER的耗电从而节省微网运行成本;另一方面可以对产热设备损耗的热能进行再利用,提升系统用能效率。