基于KM算法投切事件匹配的负荷辨识方法

胡悦,胡文山,王晓文,周东国

(1.武汉大学 电气与自动化学院,武汉 430072; 2.山东济宁圣地电业集团有限公司,山东 济宁 272000)

0 引 言

非侵入式负荷监测[1]作为一种用户侧负荷检测手段,已经成为提升智能电网智能化的重要环节之一。它不仅能增强用户体验,也能帮助电力部门了解居民的详细用电负荷构成,从而进行统筹规划[2-3],并实现能源的充分利用。为了能够实现这一目标,其依赖于内在最为关键的负荷辨识技术[4]。

负荷辨识技术本质上是针对电力负荷所表现出来的特征信息采用诸如负荷匹配、模式识别等方法进行辨识。在目前已有的众多辨识算法中,一种简单有效的方法是采用单一特征-有功功率来进行负荷辨识[5-6],它对于大功率且功率不同的用电设备,具有较好的辨识效果。然而对于有功功率相近的电器设备,辨识结果与实际投切情况会存在一定的偏差。文献[7]构建了基于谐波的电流特征表达并结合功率两个特征作为设备投切状态辨识的目标函数。同时,引入了正态分布的度量函数,将其融合并作为粒子群(particle swarm optimization,PSO)算法的适应度函数,以此寻找最佳的电力负荷分解结果。文献[8]引入了无功功率构建多特征分解模型,同时在分解模型的最优化目标函数中增加了关于电器设备特征稀疏性及工作状态转换稀疏性的惩罚项来提高分解的准确性和实用性。文献[9]提出了一种改进的基于时频分析的非侵入式监测方法,算法结合了基于多分辨率S变换的瞬态特征提取方法和基于改进的0-1多维背包算法的负载识别方法,用于识别可能同时通电的单个家用电器。文献[10]利用负荷投切时的暂态波形和功率作为特征,采用DTW算法计算测试案例与参考模板之间的相似度,通过对比特征的匹配度来识别负荷。文献[11]提出一种基于分时段状态行为的方法来提高功率相近或小功率负荷的识别准确率,具体包括:分时段提取负荷状态行为规律,构建行为模板;综合考虑概率和时间两个维度,将分时段状态概率因子(Time-Phased State Probability Factor,TSPF)作为负荷新特征引入目标函数;多特征遗传优化迭代求解。

在上述一些算法中,大多是建立在基于模式识别或者采用最优化方法的基础上,且一旦发生投入或切除时负荷事件辨识错误,则会对后续的能耗分解产生很大影响。为此,文中根据负荷事件投入和切换具有成对出现机理,将投入事件和切除事件分别作为图理论中的节点,并将负荷辨识问题转化为图论问题[12],从而采用Kuhn-Munkras算法(KM算法)将负荷投切事件的匹配问题转换为二分图[13]模型的完备匹配问题来求解。为了更好的度量KM算法中负荷事件特征与数据库中负荷特征的匹配概率,引入了Parzen窗估计方法,使电力负荷的投入/切除事件引起的特征变化与数据库中的负荷特征建立二分图最佳匹配模型,实现负荷的匹配辨识。最后,通过实验验证文中方法的有效性。

1 负荷事件检测与特征提取

负荷事件是用电负荷投切或状态改变的重要标志,也是负荷特征提取的重要依据[14]。因此,稳定可靠的负荷事件检测,是负荷辨识关键环节之一[15]。文中采用一种自适应负荷事件检测算法。

此方法将负荷事件检测过程分为两步,首先通过检测功率曲线确定是否存在负荷事件,然后采用统计学方法确定负荷事件变点。这种方式能够有效减少漏检和误检的发生,且易于实现。为了方便描述,这里假定在某个时刻点k,将时间窗内的负荷数据样本{xi}分为两类,为了避免电压、电流等波动的干扰,采用对功率曲线进行拟合逼近的方式实现负荷事件检测,其中拟合方式按窗口最小二乘拟合原则:

yt=β0+β1xt+et,t在时间窗口内

(1)

式中t为某个时刻;β0为常数项;β1为斜率项;et为误差项。当设备处于稳态运行时,通常其斜率较为稳定;而当有用电设备投切时,将会产生比较大的误差et,且斜率也会有所增加。基于此,当β1大于某个阈值时,便可确定存在负荷事件。

为了获取较为准确的负荷事件变点,这里规定在负荷事件检测窗内,将数据样本分为两类:C0类{x1,x2,…,xk}和C1类{xk+1,xk+2,…,xL},其中L为窗口内样本长度,令:

(2)

(3)

当目标函数:

(4)

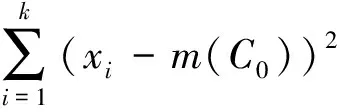
在负荷事件检测完成后,需要对负荷特征进行提取。负荷特征是用电设备运行所表现出来的特性,一般而言,有功功率P和无功功率Q是用电设备能耗的最为直接的体现,且这两个参数是负荷辨识常用的稳态特征参数[16]。负荷事件发生时表现在多种电气量发生改变,其中以有功功率最为显著,其能反映电器自身的特性[17],定义为:

(5)

而无功功率Q是用电设备属于感性、容性和阻性的一个重要参数,定义为:

(6)

此外,由于电力入口处,电压、电流等波动干扰,负荷事件变点前后简单地通过差量特征提取,可能会偏离实际的负荷投入和切除所表现出来的特征,为此,文章结合式(1)中对负荷稳态的判断,获取稳态平稳区的负荷特征进行差分提取。

2 基于图理论的负荷事件匹配

在非侵入式负荷监测中,电力负荷的投入事件和切除事件通常是成对出现的。然而,单一的投入或切除事件的辨识结果错误最终会影响负荷能耗的细分,为此,文中首先对负荷事件进行特征统计,然后针对负荷投切,分别建立投入事件和切除事件的二分图模型,再融合图论中KM算法实现负荷投入/切除的最佳匹配。

2.1 负荷特征统计

为了能够清晰描述整个匹配过程,本文约定负荷投入的事件为集合X,负荷切除的事件归类为集合Y。考虑到电流、电压等波动以及用电设备同时运行时相互干扰的特点,文中首先对每个负荷的投入/切除特征进行统计建模。

假定有n个待辨识的电器设备,对于设备i,首先用负荷事件检测方法,获取其在多个独立训练样本中的负荷特征,得到设备i投入时的有功功率跳变集合为Px={Px1,Px2,…,Pxn},相对应的切除事件的有功功率跳变集合为Py={Py1,Py2,…Pyn};投入时的无功功率跳变集合为Qx={Qx1,Qx2,…Qxn},切除时的无功功率跳变集合为Qy={Qy1,Qy2,…Qyn}。接下来,对各负荷的特征P和Q采用核密度估计中的Parzen 窗法进行估计,得到对应的概率密度函数f(x),并将其作为负荷辨识的依据,存储在数据库中。

此处为方便描述,假设{x1,x2,x3…xn}为独立同分布的n个特征样本点,则点x处的Parzen 窗核密度估计为:

(7)

式中n为样本个数;h为窗宽;K(·)为核函数。文中选择高斯函数作为核函数,即K为:

(8)

由高斯分布N(μ,σ)可知,其概率密度函数f(x)与样本标准差σ密切相关[18],其最优窗宽近似为:

(9)

则可求得负荷事件特征值x在某一负荷特征的分布下的概率为:

(10)

由此,F可作为负荷事件特征与数据库中负荷特征的匹配概率。

2.2 KM算法的基本思想

KM算法[19]是一种基于二分图理论,用来求解完备匹配下的最大权匹配的算法[20],使得在一个赋权二分图G中存在的两个互不相交的顶点集X={X1,X2,…,Xn},Y={Y1,Y2,…,Yn},X部中的每一个顶点都与Y部中的一个顶点匹配,且Y部中的每一个顶点与X部中的一个顶点匹配。

假定M为图G的匹配,M中所有边的权值之和为匹配M的权值,KM算法求解最佳匹配就是为了在赋权二分图G中寻找一个权值最大的完备匹配集,即寻找最优匹配。二分图匹配模型如图1所示。

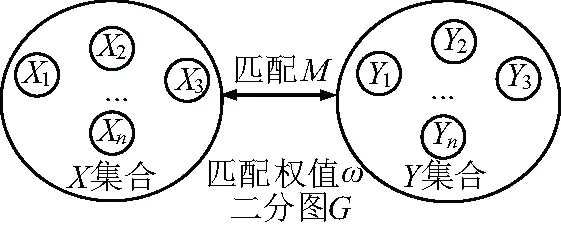
图1 二分图匹配模型

KM算法作为一种求解二分图匹配的算法,相比于匈牙利算法[21],其引入了可行顶标以及相等子图等概念,从而完成对匈牙利算法的贪心扩展[22],获得最佳的完备匹配。整个算法流程为:

1)Step1:初始化可行顶标的值。

对于原图G中的任意一个节点,给定一个函数l(node)求出结点的顶标值。为了方便描述,规定lx(x)和ly(y)分别记录集合X和Y中的结点顶标值,初始时设定lx(xi)的值为与xi相关联的边e(xi,yi)的最大权值ω(xi,yi),令ly(yi)=0,满足lx(xi)+ly(yi)≥ω(xi,yi);

2)Step2:用匈牙利算法寻找相等子图的完备匹配。

匈牙利算法采用增广路径求最大匹配,通过寻找一条增广路径P,在取反操作获得更大的匹配M’代替M,直至找不到增广路径为止;

3)Step3:修改可行顶标的值。

对于访问过的顶点x,将它的可行顶标减去d,有:

(11)

而对于所有访问过的顶点y的可行顶标增加d,其中S⊆X,B⊆Y;

4)Step4:重复Step2和Step3,直到找到相等子图的完备匹配为止。

2.3 基于改进KM算法的负荷最佳匹配

考虑到使用KM算法时,二分图两部分的节点数量不一定相等,以及在获得的负荷投切特征时,特征信息受电网电压、电流等波动的干扰影响,使得在寻找最佳匹配时存在问题,文章就此对求解过程进行改进。

首先,将投切事件的有功功率和无功功率特征与数据库负荷特征的匹配过程分别转化为四个二分图GP(X,Z),GP(Y,Z),GQ(X,Z),GQ(Y,Z);设备投入和切除事件分别为二分图的顶点集X,Y,数据库负荷顶点集为Z。定义M(xi,zj),M(yi,zj)分别为负荷投入和切除事件与数据库的一条匹配,并将X,Y与Z所对应的负荷特征匹配概率F作为匹配MG(xi,zj),MG(yi,zj)的权重ωG(xi,zj),ωG(yi,zj),其中i为负荷事件的序号,j为数据库中负荷的序号,建立负荷投切事件与数据库匹配示意图如图2所示。

图2 设备投切事件与数据库匹配模型

通常,概率的大小可表征匹配程度的大小,匹配的概率由负荷特征统计中的概率密度函数求得。因此,用KM算法所求解得到的最佳匹配结果,使得各条匹配的权重之和最大,即负荷投入事件和切除事件的特征变化与数据库中的负荷特征值最为相似。

其次针对负荷投入和切除事件的不对等性,文中将负荷事件与数据库负荷进行匹配。对于数据库中某个设备j,其与负荷事件i(i∈1-n)的有功功率、无功功率匹配概率分别为fi、hi,若满足:

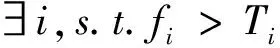
(12)

式中T1和T2为阈值,即所匹配的负荷事件具有一定的概率分布,详见式(10)。为了便于理解,这里根据不同情况将T1和T2设置如下:1)如果当用电设备可通过有功功率、无功功率可进行区分,T1和T2值可设置为0;2)当存在有功功率和无功功率都存在混叠情况,不失一般性,T1和T2的值按3σ原则进行设置,T1和T2均约设置为0.03。由此可从数据库中选择出运行的设备j,并采用KM算法匹配模型辨识出相应负荷事件对应的设备。

对于负荷投切事件,假定测试中有功功率总的匹配概率为F,无功功率匹配概率为H,则有:

(13)

(14)

其中Ei=[E(1),E(2),…,E(j),…]为事件i对应数据库中所有设备的投入/切除状态向量;E(j)∈[0,1],j为数据库中设备的序号,若E(j)为1则表示该设备发生了投切事件,否则没有发生;m为投入/切除事件总数。基于此,建立最优化匹配模型为:

(15)

式中α、β为权值,且满足α+β=1。为确定α与β值,定义μa(L)为a负荷多次重复独立量测所得特征L的多个样本的不确定度,具体计算如下:

(16)

式中Da(L)为负荷特征L的多个样本的平均值;n为特征样本总数;lk为特征L的第k个特征样本。在电气设备负荷特征区分性研究中,以各个(类)设备的某负荷特征的不确定度μ来代表a所属的簇中其他对象之间的平均距离,以两个(类)设备的某负荷特征的平均值D的差的绝对值来代表a到所有其他簇的最小平均距离,因此设备a与设备b关于某种负荷特征L的区分性系数g可定义为:

(17)

由区分性系数[23]可以得到该负荷特征L的区分性指数Gdis为:

(18)

式中s为电气设备的数量。这里区分性指数越接近1,负荷特征的区分性越好。

在计算出投切过程中有功功率和无功功率的区分性指数GPdis和GQdis后,便可得到α与β的值:

(19)

其中α+β=1,由上式可确定P,Q特征相应的权值。

3 案例实验结果与分析

文中针对某一展厅内的负荷模拟实际用电场景进行实验,并将测得的数据进行离线分析。其中测试设备包括空调、电水壶、微波炉、电磁炉、电饭煲、吹风机、电采暖、电视机共8个常见用电设备。负荷数据的采样间隔设置为2 s,数据存储到MySQL数据库中,以此验证文中方法的性能。在测试中,针对负荷事件检测方法,事件检测窗口长度为10个采样点,负荷事件斜率变化阈值为20。关于α、β值的选取,根据式(19)可得,负荷投入事件取α=0.6,β=0.4;而切除事件取α=0.5、β=0.5。另外,在实际测试中,由于阈值T1和T2设置在单个用电设备测试情况下符合情况1,因此T1和T2均为0;令式(15)加权后得到概率矩阵为[Rij]n×n,其中矩阵的某一行i中的各个数据代表某一投入/切除事件功率变化值在数据库中各负荷投入/切除功率概率密度分布曲线下的概率值。表1记录了在多次投入/切除测试下的单个用电设备有功、无功信息,反映了设备功率受电压、电流波动以及其它设备运行时的干扰(注:负荷特征采集过程中存在其他设备运行),这里将其作为负荷特征库。

表1 家庭负荷功率信息

实验中用Xi表示负荷投入事件;Yj为切除事件,i,j为负荷投入/切除顺序。图3为文章根据前文实验中对各个用电设备进行多次投切测试的统计结果,图3(a)～图3(b)为负荷投入/切除有功功率概率分布曲线,图3(c)～图3(d)为负荷投入/切除无功功率概率分布曲线。将得到的同一设备的多组独立投切实验的负荷特征跳变数据作为分析样本,并采用核密度函数绘制了概率分布图,由此可得对某个特征数据判断各负荷类别发生负荷事件的概率。

图3 设备投切时的功率特征概率分布曲线

3.1 案例一

本测试场景针对五个用电设备,其中设备投入的顺序依次为:空调、电水壶、微波炉、电磁炉、电饭煲;设备切除的顺序依次为:电水壶、微波炉、电磁炉、空调、电饭煲,其有功功率和无功功率曲线如图4所示。表2给出了案例一用负荷事件检测曲线拟合方法所获得的稳态阶段的有功功率和无功功率数据差值,并赋值为用电负荷投切的特征值。

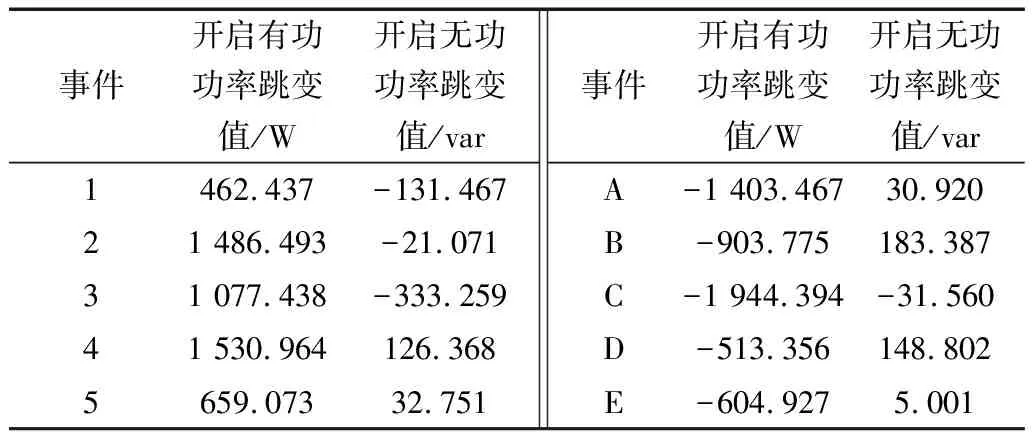
表2 案例一负荷事件特征表

图4 案例一设备投切全程有功、无功功率变化图

在案例一中,将负荷投切事件的功率跳变值代入相应的曲线中,分别根据式(10)求得各事件对应的有功投入,无功投入和有功切除,无功切除的匹配概率。然后,根据文中2.3节的方法便可从数据库中找到相应设备。图5、图6分别给出了设备投入、切除的匹配矩阵[Rij]n×n,显然匹配值越大,代表投入或切除的负荷与数据库中某一个用电设备一致的可能性越大,然后通过 KM算法计算得到的匹配结果矩阵如图7(a)、图7(b)所示。最后,得到负荷投入事件匹配结果为M(1,1),M(2,3),M(3,4),M(4,2),M(5,5),其中M(x,z)中x序号对应负荷投入事件的顺序为空调、电水壶、微波炉、电磁炉、电饭煲;z序号对应图5、图6中数据库里负荷顺序为空调,电磁炉,电水壶,微波炉和电饭煲,与实际用电设备投切事件情况匹配一致。针对负荷切除事件,得到匹配结果为M(1,3),M(2,4),M(3,2),M(4,1),M(5,5),与数据库匹配说明负荷切除的顺序依次为电水壶、微波炉、电磁炉、空调、电饭煲,结果一致。

图5 投入设备功率加权匹配矩阵

图6 切除设备功率加权匹配矩阵

图7 案例一设备投入/切除匹配结果

3.2 案例二

本测试也是针对案例一中的5个设备,其中电饭煲出现了状态不间断切换过程,即先加热,然后保温一段时间再继续运行的行为,使得实验场景更为复杂,因此最终检测到6个负荷投入和6个负荷切除事件。总体上,设备投入的顺序依次为:空调、电水壶、电饭煲、电磁炉、微波炉;设备切除的顺序依次为:电水壶、电磁炉、电饭煲、空调、微波炉,其有功功率和无功功率曲线如图8所示。所检测到的负荷投切的有功、无功特征值如表3所示。

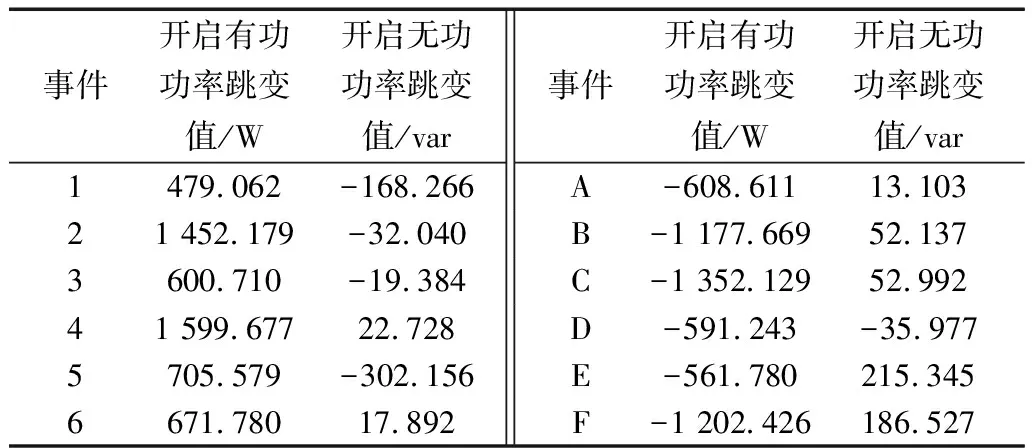
表3 案例二负荷事件特征表

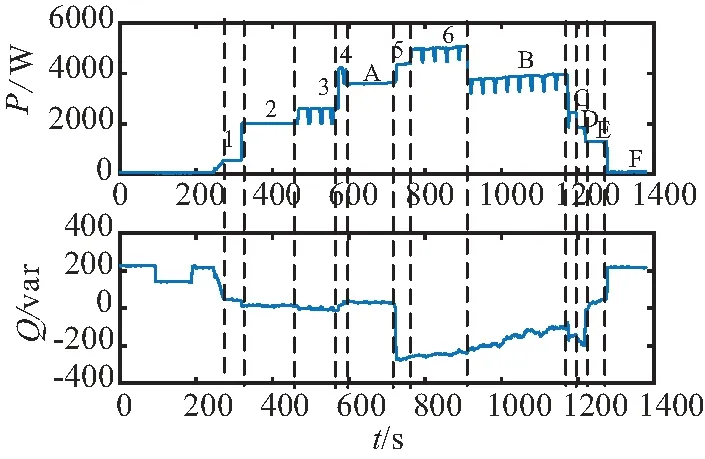
图8 案例二设备投切全程有功、无功功率变化图

在案例二中,A事件属于关闭事件,与数据库进行匹配易得其为电饭煲关闭,将A事件之前发生的事件1、2、3、4分别与数据库进行匹配可得事件3为电饭煲开启。将剩余的事件1、2、4、5、6、B、C,、D、E、F用与案例一相同的方法与数据库进行匹配,然后对概率匹配结果用KM算法进行计算,可得到结果矩阵如图9(a)、图9(b)所示。结合事件3和事件A可得到设备投入的顺序依次为:空调、电水壶、电饭煲、电磁炉、微波炉、(电饭煲);设备切除的顺序依次为:(电饭煲)、电水壶、电磁炉、电饭煲、空调、微波炉,与实际情况一致。

图9 案例二设备投入/切除匹配结果

3.3 案例三

本测试场景针对八个用电设备,其中包括了小功率设备电视机,且存在两个设备同时开启的情况,增加了负荷辨识的难度。实验中设备投入的顺序依次为:空调和电采暖(仅检测到一个负荷事件)、电视机、电水壶、微波炉、吹风机、电饭煲、电磁炉;设备切除的顺序依次为:电视机、吹风机、微波炉、电水壶、电采暖、电磁炉、空调、电饭煲,其功率曲线如图10所示。负荷投切的有功、无功特征值如表4所示。

表4 案例三负荷事件特征表

图10 案例三设备投切全程有功、无功功率变化图

由于空调和电采暖开启间隔较为接近,因此图10曲线中检测到负荷投入事件为7次。用文中2.3节提到的方法可先通过负荷关闭事件辨识出测试中包含的8个设备的类型,然后通过计算投入事件与数据库中所选出的设备的匹配概率可知,电采暖不满足式(12),因此可确定其为同时开启的设备之一。将负荷投入事件1-7分别与除去电采暖的另7个设备匹配,并用KM算法得到匹配结果。由结果可知事件1与空调匹配,其中事件1的有功功率变化为1 156.1 W,而空调的平均有功功率仅为467.3 W,由此可知事件1为空调与电采暖同时开启事件。将事件1拆分为事件1.1(空调)和1.2(电采暖)后与数据库匹配,并用KM算法得到匹配结果如图11所示。负荷切除事件匹配结果如图12所示。(注:图11和图12中矩阵各列分别代表:空调、电磁炉、电水壶、微波炉、电饭煲、吹风机、电采暖、电视机)。

图11 案例三设备投入匹配结果

图12 案例三设备切除匹配结果

由图11、图12可以看出负荷投入的顺序为:空调和电采暖(同时)、电视机、电水壶、微波炉、吹风机、电饭煲、电磁炉;与实际情况相一致。而设备切除的顺序依次为:电视机、吹风机、微波炉、电水壶、电采暖、电磁炉、空调、电饭煲,辨识结果正确。

此外,为了验证文中方法的有效性,针对案例一至案例三的辨识结果,将文中提出的辨识方法与文献[8]中的方法以及仅使用单个特征的KM算法(KM-P&KM-Q)进行比较。同时,采用Ac(单个负荷设备分解的正确率)与Acc (所有电器分解的正确率)来进行对比评价,其结果如表5所示。表5中A-c、E-k、Mw,I-c、Co、H-d、E-h、TV分别为空调、电水壶、微波炉、电磁炉、电饭煲、电吹风、电采暖以及电视机。从辨识结果可以看出,文献[8]中法对于小功率负荷的辨识能力较弱,且易受设备同时运行时电压电流波动的影响;仅用有功功率特征的KM-P方法对于有功功率相近的负荷辨识效果较差;由于负荷无功功率的可区分性较小,仅用无功特征的KM-Q方法整体的辨识效果较差;而文中方法将有功功率和无功功率进行加权,并通过KM算法进行匹配辨识能较好地克服以上问题,提高辨识准确率,获得更好的辨识效果。

表5 不同方法辨识结果

为进一步验证文中方法对实际家庭用电场景的辨识效果,采用REDD数据集中一户家庭的用电数据进行测试。测试共包括6种负荷,分别为:channel 7,channel 9,channel 11,channel 13,channel 17,channel 19。同时将文中方法与文献[24]中方法进行对比,文献[24]采用了图信号方法对负荷进行辨识,与文中方法类似。从图13中的对比结果可以看出文献[24]方法整体性能较差,其仅使用有功功率一项电气特征,对有功功率相近的负荷channel 7和channel 17辨识效果较差。随着负荷事件的增加,两种方法的准确率都有所下降且渐趋于稳定,由此可见,文中方法对实际家庭用电负荷也有较好的辨识效果。

图13 REDD数据集测试结果对比

4 结束语

文章将用电设备投入和切除的负荷事件作为图论中的节点,构建基于二分图的负荷投切事件与数据库负荷的最佳匹配模型,并提出了采用Parzen窗法对投入/切除的负荷稳态特征进行概率密度估计;建立了用电设备投入和切除特征的概率分布模型;最后采用KM算法求取设备投切事件与数据库负荷的最佳匹配,从而实现负荷的匹配辨识。通过实验验证,文中方法对实际家庭负荷运行场景具有较好的辨识准确性,且对于同时开启(不同时关)的设备和小功率设备,也具有一定的辨识能力。在下一步研究中将对数据库进行扩展,增加负荷种类,解决算法对多档位设备难以准确辨识的问题,增强算法对多状态负荷的辨识能力。