A hybrid data-driven and mechanism-based method for vehicle trajectory prediction

Haoqi Hu·Xiangming Xiao·Bin Li·Zeyang Zhang·Lin Zhang·Yanjun Huang·Hong Chen

Abstract Ensuring the safe and efficient operation of self-driving vehicles relies heavily on accurately predicting their future trajectories.Existing approaches commonly employ an encoder–decoder neural network structure to enhance information extraction during the encoding phase.However,these methods often neglect the inclusion of road rule constraints during trajectory formulation in the decoding phase.This paper proposes a novel method that combines neural networks and rule-based constraints in the decoder stage to improve trajectory prediction accuracy while ensuring compliance with vehicle kinematics and road rules.The approach separates vehicle trajectories into lateral and longitudinal routes and utilizes conditional variational autoencoder(CVAE)to capture trajectory uncertainty.The evaluation results demonstrate a reduction of 32.4%and 27.6%in the average displacement error(ADE)for predicting the top five and top ten trajectories,respectively,compared to the baseline method.

Keywords Vehicle trajectory prediction·Rule knowledge·Graph attention network·Conditional variational autoencoder·Moving horizon optimization

1 Introduction

Over the past decade, there have been high expectations for autonomous vehicles (AVs) to enhance road safety and efficiency.However, the realization of these benefits has encountered various challenges, primarily stemming from the intricate and unpredictable driving conditions [1, 2].Existing autonomous vehicle(AV)systems face difficulties in attaining the human level of accuracy in that conditions,resulting in either excessive caution or collisions[3].In complex scenarios,the precise prediction of trajectories plays a vital role in ensuring safe and efficient autonomous driving[4–7].

Trajectory prediction methods for autonomous driving can be broadly categorized into rule-based or physics-based methods,machine learning or deep learning-based methods,and planning-based methods[8].Standard kinematic prediction methods include constant velocity (CV) and constant acceleration (CA) models, constant turn rate and velocity(CTRV), and constant turn rate and acceleration (CTRA)models [9],etc.However, these physics-based methods are only suitable for short-term prediction.Kalman filter is a method that considers the prediction uncertainty based on the kinematics model.Although trajectory uncertainty is commonly modeled using a Gaussian distribution, it falls short in accurately representing the diverse behaviors exhibited by human drivers,as it assumes a unimodal distribution.Xie[2]proposed a vehicle trajectory prediction method combining physics and maneuver.Physics-based methods have traditionally excelled at ensuring short-term trajectory accuracy,while maneuver-based methods have focused on predicting long-term trajectories.However,accurately identifying driving maneuvers poses a significant challenge due to the wide range of driving styles, vehicle characteristics, and uncertain scenarios.Incorrect identification of maneuvers leads to substantial errors in trajectory predictions,underscoring the limitations of this approach.

The recurrent neural network (RNN) is a widely used deep learning method for prediction tasks.RNN and its variants, including GRU and LSTM, were initially developed and applied in the natural language processing(NLP)tasks.It is important to note that RNNs are not limited to NLP and have been successfully utilized in various domains, especially in the trajectory prediction.Deo [10] and Xin [11]first predicted the maneuver probability according to the encoder–decoder architecture of LSTM and then predicted the trajectory.Park et al.[12] discretized the highway into grids, expressed the predicted trajectory as multiple probability trajectories occupying the grid map, and obtainedKtrajectories with the highest probability through beam search.However, this method sacrifices prediction accuracy due to the 10m grid length.Effectively handling the multimodal characteristics and inherent uncertainty of trajectory prediction solely through the utilization of the RNN structure presents a challenge.Furthermore, those studies have been primarily focused on highway scenarios,limiting their applicability to other road environments.

Researchers have employed convolutional neural networks(CNNs)to encode both map information and vehicle trajectories, enabling the extraction of interaction features between vehicles and their surrounding environment.This approach significantly enhances the accuracy of vehicle trajectory prediction while effectively capturing complex interactions that occur on the road.Convolutional social pooling, proposed by Deo et al.[13] and CoverNet, proposed by Phan-Minh et al.[14], use CNN to extract map features and interaction information and predict trajectories based on RNN.During driving, traffic participants usually adopt a local perspective, focusing on nearby lanes and vehicles rather than a bird’s-eye view.While CNNs are beneficial for extracting interactive features,maps often possess graph structures with intricate topologies.This complexity makes it inefficient for 2D convolutions to capture relevant information.For instance,a lane may extend over a considerable distance in its direction.To encompass the necessary information,the receptive field of the convolutional network would need to be exceptionally large,covering not only the intended area but also a substantial portion outside the lane.Therefore,it is unsuitable for trajectory prediction problems to directly extract images from rasterized maps as input features[15].

To address the challenge of fluctuating numbers of traffic participants and effectively model their interactions,researchers have utilized graph neural networks and attention mechanisms to capture the dynamic interactions among agents.For instance, Yan et al.[16] used two types of spatial attention mechanisms to explain the interaction:attention to traffic participants and attention to lanes.Gao et al.[17]proposed a vector representation of a scene instead of a rendered image and feed the vectorized information into a graph neural network (GNN).Based on this, Deo et al.[18] used the graph attention network (GAT) to establish the interaction relationship between the target predicted vehicle and surrounding vehicles and pedestrians.Liang et al.[19]introduced a local graph attention mechanism to capture the spatial dependencies of trajectories and a temporal attention mechanism with sliding windows to capture short-and long-term temporal dependencies in trajectories.Although the attention mechanism can better capture the interaction between traffic participants,it is difficult to characterize the inherent uncertainty of the future trajectories,which can be loosely decoupled into lateral (e.g., keeping lane, turning)and longitudinal(e.g.,accelerating,braking)[18].

To tackle the uncertainty in trajectory prediction,researchers have introduced the concept of multipath and multimodal trajectory predictions (MTP).These methods,suggested by Chai et al.[20] and Cui et al.[21], respectively,simultaneously infer multiple trajectories and provide the probability of corresponding trajectories.Additionally,researchers have utilized generative methods such as conditional variational autoencoder(CVAE)[22,23]and generativeadversarialnetwork(GAN)[24]fortrajectoryprediction.Ivanovic et al.[25, 26] used discrete latent variables in CVAE to avoid the mode collapse problem.Bhattacharyya et al.[27]applied an attention mechanism to the latent variables in CVAE to better capture interactions in the latent space and accurately represent the multimodal distribution of trajectories.Li et al.[28] used two latent variables: one for representing social interaction relations between agents and the other for representing agents’intent.

Planning-based methods of trajectory prediction involve using the reinforcement learning algorithms to generate potential trajectories for vehicles by considering factors such as the current state, surrounding environment, and desired objectives.Deo et al.[6] proposed an approach based on maximum entropy inverse reinforcement learning (MaxEnt IRL), which can infer target vehicles’ goals and possible paths.Plan-based trajectories are state sequences sampled from maximum entropy policies rather than hidden variable generation.Sun et al.[29]applied a hierarchical form of the IRL approach in an interaction-aware prediction algorithm,where a mixture distribution of discrete strategies represents the future trajectory of the target vehicle.

Existing approaches, including interactive CNN, GCN,GAT, CVAE with hidden variables, and reinforcement learning-based methods, primarily focus on enhancing the modeling of historical data in the encoder phase but do not sufficiently incorporate constraints on predicted trajectories during the decoder stage,which can result in non-compliant trajectories that are detrimental to decision-making and may lead to erroneous choices.

This paper proposes a novel approach that integrates neural networks and rule-based constraints in the decoder stage to enhance trajectory prediction accuracy while maintaining adherence to vehicle kinematics and road rules.The method effectively separates vehicle trajectories into lateral and longitudinal routes,utilizing conditional variational autoencoder(CVAE)to capture the uncertainty of predicted trajectories.The contributions of this paper include the proposed method and demonstrated improvements in accuracy and compliance with vehicle kinematics and road rules:

1.This paper proposes an innovative decoding method that integrates neural networks, specifically the graph attention mechanism and moving horizon optimization(MHO),with rule-based constraints.While existing algorithms primarily concentrate on encoding interaction relations and historical data, limited studies have addressed the decoding phase.The proposed method overcomes this limitation by combining neural networks and rules, resulting in improved trajectory prediction accuracy while ensuring adherence to vehicle kinematics and road rules.

2.The extensive experiments were performed on the nuScenes, a large-scale public dataset that focuses on autonomous driving research,to quantitatively and qualitatively evaluate the proposed method against various baseline and state-of-the-art (SOTA) approaches.The results showcased a notable enhancement in predictive accuracy, constraint satisfaction, and predictive robustness by incorporating prior knowledge into the neural network.Particularly, the experiments encompassed complex interaction scenarios, underscoring the method’s effectiveness in real-world driving situations.

The rest of the paper is organized as follows: Sect.2 defines the trajectory prediction problem.Section3 presents the proposed method.Section4 compares and analyzes the method proposed in this paper with existing methods,including quantitative analysis,qualitative analysis,and robustness analysis.Finally,conclusions are drawn in Sect.5.

2 Problem definition

3 Proposed method

The method presented in this paper is built upon the encoder–decoderarchitectureofCVAE.CVAEencodestheunderlying stateintoaprobabilitydistributionandutilizessamplingfrom this distribution to generate diverse outputs.It allows the model to learn the posterior probability distribution of the true latent state variable,making it well suited for addressing model-based planning and control challenges [25],specifically in the context of autonomous driving decision-making tasks.

The overall framework of the proposed method is shown in Fig.1.This paper uses LSTM and GAT to encode the historical information,future information of the target vehicle and surrounding agents,and lane information.Figure1 introduced the encoder,decoder,and overall framework of CVAE in detail.

3.1 Encoder based on temporal encoding and spatial attention

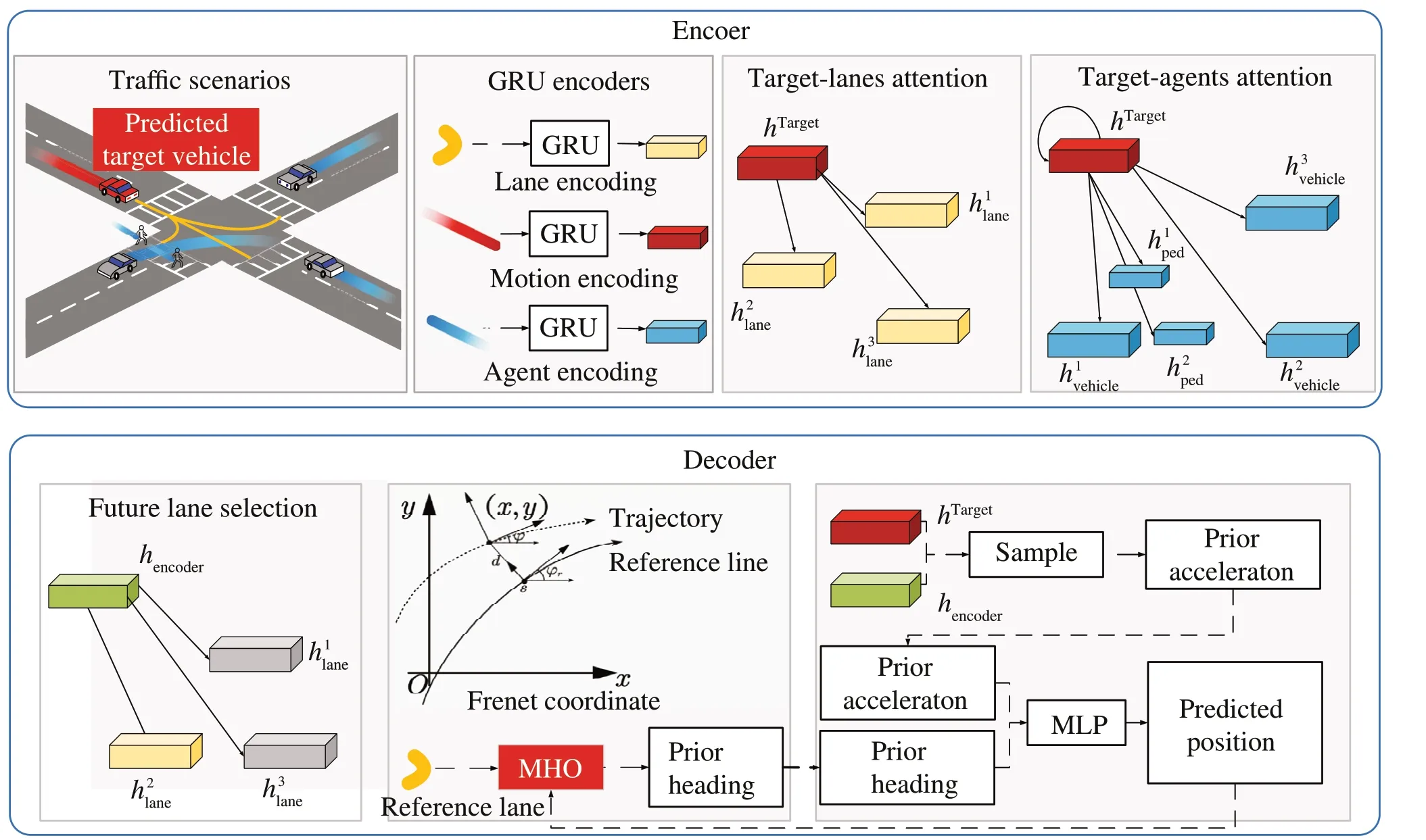
Fig.1 Proposed trajectory prediction framework

The encoder based on temporal encoding and spatial attention is shown in Fig.1.First,traffic flow and road information are extracted.The input information is a piece of historical data for predicting the target vehicle and other traffic participants around it.In this paper,the method initially used a fully connected network and a nonlinear activation function to embed the time series data,followed by the utilization of LSTM for encoding it.The method can be expressed as:

where FC is a fully connected network.This paper sets different maximum numbers for different agent categories,meaning that the number of agents the target vehicle pays attention to has an upper limit.For some scenarios where the number of agents does not reach the upper limit,fill the excess with 0 and mask this part to handle different numbers of traffic participants adaptively.

Although lane information is not inherently time-related data,it can be considered as sequence data.LSTM is utilized to encode the lane information in the proposed method:

Adaptive processing of different lane numbers is achieved in an agent-like manner.

Simply adopting temporal encoding cannot fully represent the traffic scenario and capture agent interaction.Graph neural network is suitable for capturing the interaction relationship in dynamic scenarios since GAT can aggregate the information of adjacent traffic participants by assigning different weights to different nodes.This paper uses a graph attention network to model interaction.The calculation of the attention weight for the target vehicle and the agent is given by

where the adjacent agent agent represents a vehicle or pedestrian,Wrepresents the shared weight to be learned in GAT,arepresents the weight vector of the feed-forward neural network,and||represents the vector connection.

After obtaining the normalized attention coefficientα,the output of the graph neural network is expressed as

whereσis a nonlinear activation function.The above formulas can also express lanes’attention.Each interaction learns a set of network parameters.

3.2 Decoder combining neural network and receding optimization

According to the characteristics of vehicle trajectory prediction on structured roads, this paper divides trajectory prediction into lateral heading angle prediction and longitudinal acceleration prediction.Longitudinal decoding and lateral decoding are introduced separately.

3.2.1 Longitudinal acceleration prediction

To better characterize the prediction uncertainty, this paper does not directly predict the continuous value of the acceleration.However,itpredictstheaccelerationafterdiscretization,which has also obtained better results than directly predicting the acceleration value in the experiment.In addition,predicting the discrete accelerations can better guarantee vehicle dynamics constraints.According to the physical constraints of the vehicle,first set the maximum and minimum accelerations of the vehicle asamaxandamin,respectively,and the candidate accelerations are as follows:

InSect.3.2.1,theencodedinformationhhasbeenobtained,including target vehicle informationhTarget, interaction information with surrounding traffic participantshvehicle,hpedestrian,and lane interaction informationhlane.Firstly,the longitudinal discrete latent variablezlng,1:Tfutureis obtained according toh,expressed as

Then, sample the acceleration labelalabel,1:Tfuturefromzlng,1:Tfuture,shown as

Finally, the corresponding acceleration can be obtained according to the label obtained by sampling.

3.2.2 Lane selection

Since there is lane guidance,the calculation of the heading angle is different from the acceleration.It does not entirely rely on the neural network but can be combined with prior rule knowledge.First,according to the encoding informationh,the sampling is obtained to obtain the lateral latent variablezlat:

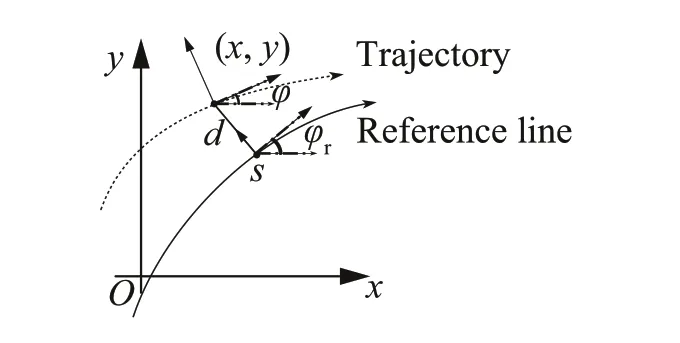
Fig.2 Schematic diagram of the frenet coordinate

Then,useGATtocalculatetheprobabilityof thecandidate lane,expressed as follows:

Next,in combination with road information,we estimate the possible heading angle in the future via MHO.

3.2.3 Heading angle estimation

In structured roads,the heading angle of the vehicle can be estimated based on prior knowledge, such as the candidate lanes that the target vehicle can drive.For the convenience of calculation,this paper calculates the heading angle in the frenet coordinate system shown in Fig.2.The vehicle model in the frenet coordinate system is as follows:

whereϕrandκrare the heading angle and curvature of the candidate path,respectively.

In this paper,when the lane closer to the vehicle position is used as the candidate reference path,dis small,and the road’s curvature is assumed to be small.To simplify the solution of the heading angleϕ,the speed is used as a constant,that is,˙s≈V, then model (10) simplifies to the following linear model:

Takingϕras the measurable external disturbance,(11)can be written in the following form

whereAc=0,Bc,ϕ=V,Bc,w=-V.

Discretize the model to get

Let the prediction horizon beNpand the control horizon beNc,and define the prediction vector,heading angle vector,and measurable disturbance vector as follows:

The prediction equation is as follows:

where

The goal is to drive along the candidate trajectory, i.e.,dref= 0.Therefore, considering the requirements of reference path tracking and path smoothing at the same time,the prior heading angle is obtained by receding optimization of the following objective function:

Define the error vector asE(k+1) = -Sdd(k) -SwW(k),then the heading angle obtained is

Take the first valueϕ∗(k) =Φ∗1(k) of the optimization variable as the predicted value of the heading angle at this moment.For the target vehicle, iteratively predictsTfuturetimes.The trajectory prediction model is introduced in Sect.3.2.4.

3.2.4 Trajectory prediction

The heading angle and acceleration sequence here are obtained by solving the open-loop optimization control problem, reflecting the possible future driving direction of the vehicle.After getting the estimated heading angleϕtand accelerationatcorresponding to each path,a minor correction is made using the neural network based on the hidden variableh,expressed as follows:

whereu=[ϕ,a].

Predict future trajectories based on the following kinematic model:

Finally,a Gaussian distribution is used to characterize the uncertainty of the final position, expressed asˆXt, ˆYt～N(μt,Σ), whereμt=(Xt,Yt).For simplicity, the predicted locations share the covariance matrix

3.3 Trajectory prediction based on CVAE

Based on the encoder and decoder proposed in Sect.3.2,the trajectory prediction problem defined in Sect.2 of this paper can be solved.Under the given traffic flow information and road information,the position distribution of the target vehicle for a specific time in the future can be predicted,expressed as follows:

where

whereθis the parameter of neural networks.

Due to hidden variableszlatandzlng, it is not simple to directly maximize the likelihood function,the network parameters are trained by stochastic variational inference based on pyro[30].

4 Experiment

4.1 Experimental design

4.1.1 Dataset

This paper evaluates the proposed trajectory prediction method based on the public dataset nuScenes [31], an autonomous driving dataset collected in two traffic-dense urban driving environments, Boston and Singapore.The nuScenes data frequency is 2Hz, and the trajectory prediction task is to predict the trajectory of the next 6s based on the data of the past 2s at most.

4.1.2 Evaluation metrics

This paper follows the evaluation methods in nuScenes and selects the following metrics as quantitative evaluation metrics for trajectory prediction:

1.Minimum average displacement error (ADE) overKpredicted trajectories (min ADEK): the average displacement error between the reference trajectory in theK-predicted trajectories and the actual trajectory is expressed as follows:

whereNisthenumberoftrajectoriesinthedataset,Tfutureis the prediction steps,sgtis the actual trajectory in the dataset,andskis the predictedkth trajectory.

2.Minimum final displacement error (FDE) overKpredicted trajectories (min FDEK): the final position displacement error between the best trajectory in theK-predicted trajectories and the actual trajectory is expressed as follows:

3.Miss rate (MR) at 2ms overK-predicted trajectories(MRK): among the predictedK-trajectories, if the predicted point closest to the actual trajectory still deviates from the actual value by more than 2m,it is called a miss,and the miss rate is the ratio of the missed trajectory to the whole dataset.

4.Off-road(OR)rate overK-predicted trajectories(ORK):among the predictedK-trajectories,if all the trajectories exceed the drivable area, it is called off-road.The offroad rate is the ratio of off-road trajectories to the whole dataset.

In this paper,various experiments are carried out to verify the effectiveness and advantages of the proposed method,including:

1.Quantitatively and qualitatively analyze the method proposed in this paper with the baseline and SOTA methods in nuScenes.

2.Conduct ablation studies on some critical components in the model,and try to explain why combining prior knowledge can improve trajectory prediction performance.

3.Evaluate prediction robustness under sensor noise and target loss.

4.1.3 Implementation details

According to the introduction in Sect.3, the method proposed in this paper mainly comprises temporal encoding,spatial encoding, CVAE, lateral decoding, and longitudinal decoding.The parameters of each module are shown in Table1.Among them,input_size=32,hidden_size=32 of LSTM,embed_dim=32,num_heads=4 of multi-head attention,and the hidden layer dimensions of the two-layer fully connected network are 32 and 128,respectively.In this paper,the initial learning rate is set to 1e-3,and after 6 epochs,it is reduced to 1e-5 according to the exponential decay rate,and a total of 10 epochs are trained.

Table 1 The structure of each part of the proposed method

4.2 Quantitative analysis

4.2.1 Comparison method

This paper quantitatively compares the proposed method with the baseline and some SOTA methods in nuScenes,including the following methods:

1.Physics Oracle(nuScenes baseline)[31]:A single-modal method that predicts future trajectories based on physical models and current vehicle state,regardless of prediction uncertainty.

2.CoverNet (nuScenes baseline) [14] and MTP [21]: A fully connected neural network method based on raster map input and trajectory features.This paper considers the multimodal property of future trajectories,so the neural network outputs multiple trajectories and corresponding probabilities simultaneously.

3.Trajectron++[26]:CVAEmethodbasedondiscretelatent variables,encoding the trajectory information of the target vehicle and surrounding vehicles through LSTM,encoding the influence between agents through the attention mechanism, and decoding the predicted trajectory through GRU.

4.SG-Net[32]:A method based on target estimation,which completes the trajectory prediction task through three steps: predicting possible targets, generating trajectory sequences,and estimating trajectory likelihood.

In addition, the trajectory prediction method based on CVAE and MHO proposed in this paper is denoted as TPCM.

4.2.2 Comparison results

Table2 shows the quantitative comparison of the proposed TPCM prediction method with various contrasting algo-rithms in the nuScenes prediction task.The best results for each metric are indicated in bold.

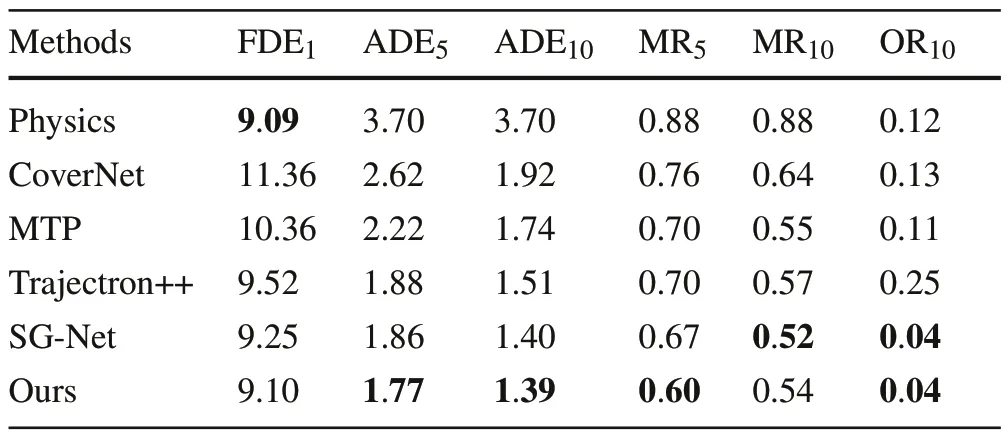
Table 2 Comparison of performance metrics of various forecasting algorithms

Among the methods listed,the average errors ADE5and ADE10of the prediction based on the physical model are the largest.Since it is a single-mode method that does not consider the uncertainty of the future trajectory,the average error of the prediction is identical no matter whatKis.It is worth noting that when predicting a single trajectory,the endpoint error of the prediction method based on the physical model has almost the same minimum value as that of the proposed method, which indicates that although existing deep learning-based algorithms take into account the multimodal nature of the future trajectory, it is difficult to predict the correct probability of the actual trajectory.Fully connected neural network methods based on raster map input and trajectory features,such as CoverNet and MTP,have achieved better results than physics-based methods when outputting multiple trajectories.The average trajectory error decreases as the number of predicted trajectories increases.For the two most commonly used metrics,ADE5and ADE10,the method proposed in this paper have decreased by 32.4%and 27.6%relative to CoverNet, 20.3% and 20% relative to MTP, and 5.9%and 7.9%relative to Trajectron++.

Among various methods,the off-road rate of Trajectron++is as high as 0.25, which means that in 25% of the cases,theKtrajectories predicted by Trajectron++are beyond the vehicle’s drivable area, which is not available for decisionmaking and planning for autonomous driving.The method proposed in this paper achieves the best off-road rate performance because we add prior rule knowledge to the neural network by receding optimization.The off-road rate of SGNet based on the target estimation method is also very low because the target points estimated by SG-Net are all in the drivable area.In the case of predicting multiple trajectories,most of the trajectories meet the lane constraints, but even so, there will still be some trajectories beyond the road.In comparison, the method proposed in this paper adds prior knowledge.Most predicted trajectories can satisfy the road constraints,which can be better seen in qualitative analysis.

Table 3 Quantitative ablation study of the proposed method

4.2.3 Ablation study

This paper also analyzes the importance of each component of the proposed method.The proposed method mainly includes three parts:encoder,decoder,and CVAE.The comparison results are shown in Table3.

Compared with the full TPCM,the performance of other ablation models deteriorates.Through the comparison of the above three parts,the following conclusions can be drawn:

1.From the comparison between the first line and the fourth line in Table3, it can be seen that when the encoder part does not use the graph attention mechanism, all performance indicators decline, which shows that the attention mechanism helps to capture the interaction between agents,and thus improve the predictive performance.

2.It can be seen from the second and fourth lines that if the prior knowledge of the road is not added in the decoder stage, the prediction performance will deteriorate sharply, which shows that the prior knowledge is beneficial to the trajectory prediction problem.Figure3 can be used to explain this phenomenon.When no prior knowledge is added,the future heading angle and acceleration can only be learned through the dataset,which is a complicated fitting problem.When adding road prior knowledge,possible future heading angles can be calculated in advance, equivalent to reducing the complexity of the original complex fitting problem, and can better learn the trajectory distribution of the dataset.

3.Comparing the third and fourth lines verifies the advantages of using discrete latent variables.The discrete distribution can better represent the multi-modes than the continuous Gaussian distribution.In particular, discrete latent variables can better capture acceleration changes.

4.When comparing the first three rows, it can be found that adding the prior information of lanes is the most helpful for trajectory prediction, followed by adopting discrete latent variables and,finally,the graph attention mechanism.When only the graph attention mechanism is removed, although the prediction performance has deteriorated, the deterioration is slight, such as ADE5and ADE10,which only increased by 0.56%and 0.72%,respectively.If no prior knowledge is added, the above two errors increase by 45.2% and 36.7%, respectively.The role of discrete latent variables is between the two,and the errors increase by 33.9%and 10.1%.

Fig.3 Simplification of fitting problem by prior knowledge

4.3 Qualitative analysis

4.3.1 Comparison method

This paper also conducts a visual qualitative analysis of the proposed method to further explore the differences and advantages of the proposed method compared with existing methods.This section qualitatively compares the following methods:(1)MTP[21];(2)Latent variable-based decoding model (LVM); (3) Goal estimation-based method (Goalbased);(4)The top five SOTA method PGP with open source code in the nuScenes leaderboard[18];and(5)The method proposed in this paper without MHO (TPC); (6) The proposed method including all components(TPCM).

4.3.2 Comparison results

This paper selects typical scenarios such as driving straight at intersections,changing lanes to overtake,driving on ramps,diversion road, T-junctions, junctions, and roundabouts to compare the above 6 methods.The visualization results are shown in Fig.4.The yellow arrows in the figure point to the endpoints of thefivepredictedpossiblefuturetrajectories and mark the probability of each predicted trajectory.The green arrows point to the endpoints of the future ground truth(GT)trajectories.In this paper, the 6 methods are appropriately arranged to compare the methods with similar prediction results by column and compare the methods with a significant difference in prediction results by row.

Figure4a–c are three relatively simple scenarios representing going straight at the intersection,changing lanes to overtake,and driving on the ramp.Multiple targets predicted by various methods can always cover the trajectory when driving on a straight road.Most methods can get the predicted trajectory closest to the real trajectory with the maximum probability.Latent variable model (LVM)-based decoding methods can generate different trajectories but have poor lateral diversity, always predicting different trajectories along the same route.The goal-based method(Goal-based)also haspoor lateral diversity in most scenarios,and in the straightgoing scenario in Fig.4a, the goal-based method predicts a goal that the vehicle cannot reach.In addition,as shown in the roundabout scene in Fig.4g,even if a reasonable target is predicted,goal based may not obtain an appropriate trajectory.The ramp in Fig.4c is a relatively simple scene because the vehicle only has one road, but MTP and TPC predict multipletrajectories beyondtheroad.Inthecurvedroadovertaking scenario in Fig.4b,the results predicted by LVM and goal based are not accurate, which is because the methods mentioned above do not utilize prior knowledge of road information,so they cannot be applied in the decision-making and planning tasks of autonomous driving.The method TPCM proposed in this paper gives the best prediction results in these three scenarios.The predicted trajectories meet the road rule constraints,and the correct results are obtained with the maximum probability.Through the comparison with TPC,it can be shown that utilizing road prior knowledge in the decoder stage can significantly improve the effectiveness and accuracy of trajectory prediction.Followed by PGP,its predicted results are also within the road, but it does not get accurate results with the maximum probability in the straight lane in Fig.4a and the ramp in Fig.4c.

Fig.4 Visual comparison of various trajectory prediction methods in various scenarios.The yellow arrows point to the endpoints of the five predicted possible future trajectories and mark the probability of each trajectory.The green arrows point to the endpoints of the future GT trajectories

Table 4 Robustness analysis of prediction when object loss

Figure4d–f are three more complex scenarios:road diversion,intersection turning,and T-junction turning.Among the three scenarios,MTP and TPC have the worst prediction performance,followed by LVM.Especially when turning at an intersection, the three kinds mentioned above of methods all fail.In comparison,the multiple trajectories obtained by Goal-based can cover the real trajectories,but there are still some unreachable predicted targets whose prediction results exceed the road boundary.The best methods for predicting results are still TPCM and PGP.There are some subtle differences between the two.First,the prediction results of TPCM are relatively conservative.As shown in Fig.4e,although the vehicle tends to turn at the intersection turning, and both methods predict the real trajectory with the highest probability, TPCM still predicts the trajectory of going straight,assigns low probabilities of 0.148 and 0.025.Second, as shown in Fig.4f,the result of PGP prediction does not fully satisfy the road constraints because it makes full use of road data as much as possible in the encoder stage rather than using road prior knowledge in the decoder stage as in this paper.

Finally, Fig.4g shows the trajectory prediction results at the roundabout.For the trajectory prediction task, the roundabout is a very complex scene because it is difficult to accurately predict which road the vehicle will exit the roundabout.Methods based only on deep neural networks such as LVM, MTP, goal-based, and TPC all fail at roundabouts.Only PGP and TPCM predict good results,but they still cannot predict accurate results with maximum probability but can only predict possible future trajectories.TPCM gives more diverse results and better characterizes the inherent uncertainty of trajectory prediction.

4.4 Predictive robustness analysis

In the last section,this paper analyzes the predictive robustness of the proposed method.Although the nuScenes dataset provides continuous tracking results for detecting objects,autonomous vehicles will inevitably encounter complex realworld situations, for example, object loss.Object loss is simulated by randomly discarding part of the data.Previous quantitative and qualitative analyses found that PGP is the best among the comparison methods.This paper only compares the prediction robustness of the proposed method with PGP.The comparison results are shown in Table4.

Table4 compares the two methods for 20% and 40% of missing data.When data are missing,the prediction errors of both methods increase, but the deterioration rate of TPCM is still much smaller than that of PGP.When the data are lost by 20%, the deterioration rate of TPCM indicators is about 10%, while the deterioration rate of most metrics of PGP exceeds 100%.When the data are lost by 40%, each metric of TPCM deteriorates by about 20%.In comparison,the prediction error of PGP increases by more than 200%.At this time,the prediction results can hardly be applied to the decision-making and planning tasks of autonomous driving.

Compared with the current SOTA method PGP, the method TPCM proposed in this paper has outstanding predictive robustness,which is because TPCM adds prior road knowledge in the decoder stage, combined with MHO, to calculate the possible future heading angle of the vehicle in advance,thus adding road constraints and vehicle lateral kinematics constraints.In addition, the obtained acceleration is guaranteed to satisfy the longitudinal constraints of the vehicle by predicting the acceleration.Most current neural network-based methods cannot impose constraints on the predicted trajectory.If the data are noisy or missing, the impact on the prediction results will be so significant that it may not be possible to apply the prediction model to the decision-making and planning tasks of autonomous driving.The method proposed in this paper overcomes this shortcoming.

5 Conclusion

In this paper,a novel vehicle trajectory prediction is proposed based on the advanced neural network and prior knowledge.The neural network is completed based on the encoder–decoder architecture of CVAE, and the prior knowledge is incorporated into the decoder of neural network by MHO.The quantitative and qualitative analysis of experimental resultsshowsthattheproposedmethodhaspreciseandrobust performanceonvehicletrajectoryprediction.Futureresearch includes: (1) adding more prior knowledge, such as intersection and traffic light information, etc.; (2) applying the proposed trajectory prediction method to decision-making and task-planning for autonomous driving.