Semi-global weighted output average tracking of discrete-time heterogeneous multi-agent systems subject to input saturation and external disturbances
2023-11-16QilinSongYuanlongLiYijingXieZongliLin
Qilin Song·Yuanlong Li·Yijing Xie·Zongli Lin
Abstract In this paper, we revisit the semi-global weighted output average tracking problem for a discrete-time multi-agent system subject to input saturation and external disturbances.The multi-agent system consists of multiple heterogeneous linear systems as leader agents and multiple heterogeneous linear systems as follower agents.We design both the state feedback and output feedback control protocols for each follower agent.In particular, a distributed state observer is designed for each follower agent that estimates the state of each leader agent.In the output feedback case,state observer is also designed for each follower agent to estimate its own state.With these estimates,we design low gain-based distributed control protocols,parameterized in a scalar low gain parameter.It is shown that,for any bounded set of the initial conditions,these control protocols cause the follower agents to track the weighted average of the outputs of the leader agents as long as the value of the low gain parameter is tuned sufficiently small.Simulation results illustrate the validity of the theoretical results.
Keywords Distributed average tracking·Input saturation·Low gain feedback·Heterogeneous multi-agent systems·Output regulation
1 Introduction
The problem of multiple agents each tracking the average of multiple time-varying signals, each associated with one agent, using the information of its neighboring agents is called distributed average tracking [1, 2].Distributed average tracking problem has numerous applications in multi-agent systems including distributed estimation, distributed optimization and distributed formation control.The continuous-time distributed average tracking problem has been widely studied [3, 4].Specifically, Reference [3] presented distributed discontinuous control algorithms that achieve distributed average tracking for time-varying signals with bounded derivatives.Reference [4] designed eventtriggered average tracking algorithms for heterogeneous agents to achieve average tracking of time-varying signals.Reference[5]studied the distributed average tracking problem in the discrete-time setting.
Actuator limitation is ubiquitous in practice and, as a result, research on control systems with input saturation has been widely conducted.For example, low gain feedback laws[6]were proposed to achieve semi-global output regulation of the discrete-time linear systems that are asymptotically null controllable with bounded controls(ANCBC).A discrete-time linear system is said to be ANCBC if it is stabilizable and all its open-loop poles are on or inside the unit circle.Reference [7] studied cooperative output regulation for a discrete-time time-delay multi-agent system.Reference[8]presented an adaptive distributed observer for cooperative output regulation of a discrete-time multi-agent system so that the follower agents do not need the system matrix of the leader agent.Reference [9] studied the problem of semi-global leader-following output consensus whenthefolloweragentsarerepresentedbydiscrete-timelinear systems with input saturation and external disturbances.More recently, Reference [10] formulated and studied the semi-global weighted output average tracking problem for a multi-agent system, whose follower agents are heterogeneous and represented by continuous-time linear systems with input saturation and external disturbances.Both the reference signals, whose average is to be tracked by the follower agents, and the disturbances are generated by the leader agents that are also heterogeneous and represented by continuous-time linear systems.In addition, such a formulation does not require the number of leader agents and the number of follower agents to be the same.
In this paper,we focus on the semi-global weighted output average tracking problem for a multi-agent system whose heterogeneous agents are described by discrete-time linear systems with input saturation and external disturbances.We first construct,for each follower agent,distributed observers to estimate the states of the leader agents.In the output feedback case, a state observer is also constructed for each follower agent to estimate its own state via output information.We then utilize the low gain feedback design technique and the output regulation theory to design distributed state feedback and output feedback control laws to achieve semiglobal weighted output average tracking.We note that the discrete-time results we are to present are not direct extensions of[10].In particular,the continuous-time leader state observers constructed in[10]rely on high-gain action.The value of the gain parameter in the distributed observer is chosen sufficiently high to ensure a Hurwitz system matrix in proving the stability of the error dynamics.However,the stability property of the corresponding system matrix in the discrete-time setting is much more complicated than the continuous-time case.As a result, we have to resort to more subtle property of the system matrix under an additional assumption on the system matrix of the leader agent to ensure its stability[7].Partial results from this paper were presented at a conference [11], which focuses on the state feedback results.
Organization of the paper Sect.2 formulates the semiglobal weighted output average tracking problem for a multiagent system, where the leader agents are represented by discrete-time heterogeneous linear systems and the follower agents by discrete-time heterogeneous linear systems with input saturation and external disturbances.In Sects.3 and 4,we respectively design distributed state feedback and output feedback control protocols that solve the problem formulated in Sect.2.Section5 presents numerical examples to illustrate the theoretical results.Section6 concludes the paper.

2 Problem formulation
We focus on a multi-agent system containingMheterogeneous leader agentsvk,k∈I[1,M],andNheterogeneous follower agents,vi,i∈I[M+1,M+N].The dynamics of each leader agentvkis described by
wherewk(t)∈Rskis the state,zk(t)∈Rqis the output,andWk0⊂Rskis bounded.LetW0=W10×W20×···×WM0.The dynamics of each follower agentviis described by


Lemma 1 [12]Under Assumption 1,all the eigenvalues of Mk,k∈I[1,M],have a positive real part.
Lemma 2 [13]For the matrix
let aik> 0,i∈I[M+ 1,M+lk],and aik= 0,i∈I[M+lk+1,M+N],and the matrixLk be partitioned as

Assumption 2 For eachk∈I[1,M], all eigenvalues ofSkare on or inside the unit circle.
Assumption 3 For eachi∈I[M+1,M+N],(Ai,Bi)is stabilizable and all eigenvalues ofAiare on or inside the unit circle.
Assumption 4 For eachk∈I[1,M],(Sk,Qk)is detectable.
Assumption 5 For eachi∈I[M+1,M+N],(Ai,Ci)is detectable.
Lemma 3 [14]Under Assumption 3,for any ε∈(0,1],there is a unique matrix Pi(ε)>0,i∈I[M+1,M+N],which solves the following algebraic Riccati equation(ARE):

Assumption 7 For eachi∈I[M+1,M+N],there are a positive scalarδ<Δand a non-negative integerTsuch that,for allw(0)∈W0,‖Γiw(t)‖∞,T≤Δ-δ.
Since not all follower agents know the states of all leader agents, we design, for each follower agentvi,i∈I[M+1,M+N],distributed leader state observers to estimate the states of the leader agentsvk,k∈I[1,M],as follows:
whereμkis chosen according to Lemma 4.
Note that for follower agents that have access to the leaders, state observers are not needed.For simplicity in presentation, we have built state observers for all follower agents.
We introduce the following notation to help formulate the problem:
The problem we are to solve for the multi-agent system consisting of(1)and(2)via state feedback can be formulated as follows.
If the states of the leader agents and the follower agents are not available for the implementation of the control laws,we need to construct state observers to obtain the information of these states.
For eachk∈I[1,M],define
According to whether the follower agentvihas access to the information of the leader agentvk,we design the following two kinds of distributed leader state observers to estimate the states of the leader agents.They directly use the output information of the leader agentvkor the state of their neighbors’leader state observers to obtain their estimates of each leader’s state.
where ˆwik(t)is the estimate of the state of the leader agentvk, the value ofτkwill be determined later, andLkis such thatSk+Lk Qkis Schur.The existence ofLkis guaranteed as(Sk,Qk)is detectable.
For each follower agentvi,i∈I[M+1,M+N], we design the following state observers to estimate its own statexi:
The problem we are to solve for the multi-agent system consisting of(1)and(2)via output feedback can be formulated as follows.

3 State feedback case
Using the states of the distributed leader state observers(6),we construct,for each follower agentvi,i∈I[M+1,M+N],the following low gain feedback control protocol:
where
andPi>0 solves the ARE(4).
Denote
We have
For notational brevity,we will denoteΥ(ε)byΥandΥi(ε)byΥi.
Theorem 1Consider the multi-agent system(1)–(2).Suppose Assumptions 1,2,3,6 and 7 hold.Then,with the control protocols(10),for any a priori given,arbitrarily large,bounded sets of initial conditions X0⊂Rn andthere exists ε∗∈(0,1]such that,for any ε∈(0,ε∗,the output tracking errors satisfy
ProofDenote the observer errors as
Then,it follows from(1)and(6)that
For eachk∈I[1,M],let
Then,we have
whereRk=(IN⊗Sk)-μk(Mk⊗Sk).Recall thatμkis chosen according to Lemma 4.By Lemma 4,Rkis Schur.We further let
and have
whereR=diag{R1,R2,...,RM}.Clearly,Ris Schur.
We congregate the dynamics of all leader agents (1) as follows:
whereS=diag{S1,S2,...,SM}.Similarly,the dynamics of all follower agents(2)can be congregated as follows:
where
and
Let
Then,the regulator Eq.(5)can be rearranged in a congregated form as
Denoteξ(t)=x(t)-Π¯w(t).In view of(12)–(14),we have
Letψi∈RNsbe the vector withith element being 1 and all other elements being 0.In view of the definitions of ¯w(t),˜w(t)and ˆw(t),we have
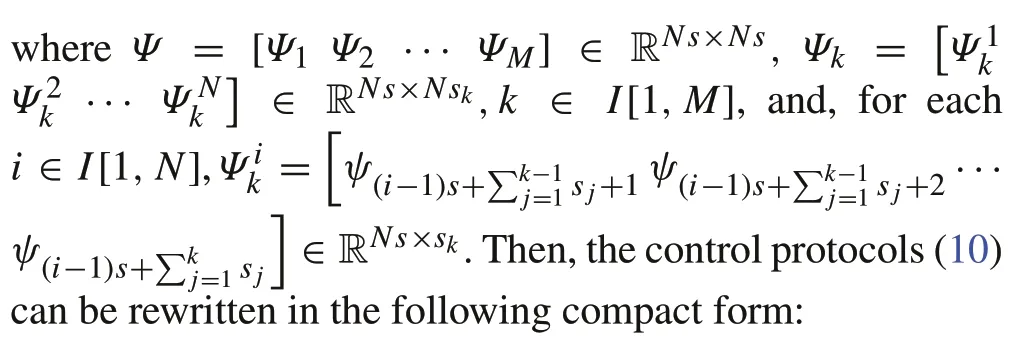
whereE1=(Υ Π+Γ)Ψ.
LetH=A-BΥ.In view of the ARE(4),
and
Since limε→0P(ε)=0,there is a constantη1>0 such that,for anyε∈(0,1],
SinceRis Schur,there exists a positive definite matrixG1∈RNs×Nsand a constantκ1>0 such that
Noting that
we have
and thus
Define
We have
Consider the Lyapunov function
SinceRis Schur,for any initial condition ˜w(0)∈W0,there is a finite integerT1≥Tsuch that,for allε∈(0,1],
Note thatξ(t) is the solution of a linear difference equation with bounded inputsσΔ(u) andΓ¯w.Clearly,ξ(T1)belongs to a bounded setXξ(T1), independent ofεfor all.Letcbe a positive constant such that
Define
Letε∗∈(0,1]be such that,for allε∈(0,ε∗,
The existence ofε∗is guaranteed since limε→0Υ(ε) = 0.Assumption 7 indicates that‖Γ¯w‖∞,T1≤Δ-δ,and hence,‖u‖∞,T1≤Δ,implying thatσΔ(u)=u,t≥T1.As a result,(15)simplifies to
Substituting(16)into(17),we obtain
Recall thatH=A-BΥ.Then,
With(11),we derive
Evaluating the time difference ofValong the trajectories ofξand ˜winsideLV(c),we have
which indicates that
Thus,
In view of(14),we have
from which we have
This completes the proof.■
4 Output feedback case
Whenthestateofthefolloweragentvi,i∈I[M+1,M+N],is not available for implementation of the feedback control law(10),we construct the following output feedback control protocol(18)using its state observer(9):
Theorem 2Consider the multi-agent system(1)–(2).Suppose Assumptions 1-7 hold.Then,with the control protocols(18),for any a priori given,arbitrarily large,bounded sets of initial conditions X0⊂Rn,X0⊂Rn andW0⊂RNs,there exists ε∗∈(0,1]such that,for any ε∈(0,ε∗,the output tracking errors satisfy
ProofDenote the observer errors as
Fori∈Ik,by(1)and(7),we have
Fori∈¯Ik,by(1)and(8),we have
Fork∈I[1,M],denote
Denote
andLk∈RN×Nas the Laplacian matrix associated withAk.Let
By Lemma 2,Lkcan be written as(3).With(20),it is proved that
Thus,

the matrix
is Schur.Letqibe theith standard basis vector in RN.Note that

Then,
where
is Schur.
Denote the estimation errors as
In view of(2)and(9),we have
Denote
Then,
where
SinceAi-L X,iCi,i=I[M+1,M+N],are Schur,H1is Schur.
Let
Then,in view of(23)and(24),we have
where
Since bothH1andHvare Schur,H0is Schur.Thus,system(25)is asymptotically stable.
Note that ˆw(t)- ¯w(t)=Ψ˜w(t)and ˜x(t)= ˆx(t)-x(t).Let
Following an analysis similar to the analysis in the proof of Theorem 1,we obtain
and
whereE2=[-Υ(Υ Π+Γ)Ψ].
LetH=A-BΥ.Since limε→0P(ε) = 0,there exists a constantη2>0 that satisfies
SinceH0is Schur,there exist positive definite matrixG2∈RNs×Nsand constantκ2>0 such that
Noting that
we have
and thus
Define
We have
Consider the following Lyapunov function:
Recall that system (25) is asymptotically stable.Thus, for any initial valuesζ(0)and allε∈(0,1],there exists a finite integerT2≥Tsuch that
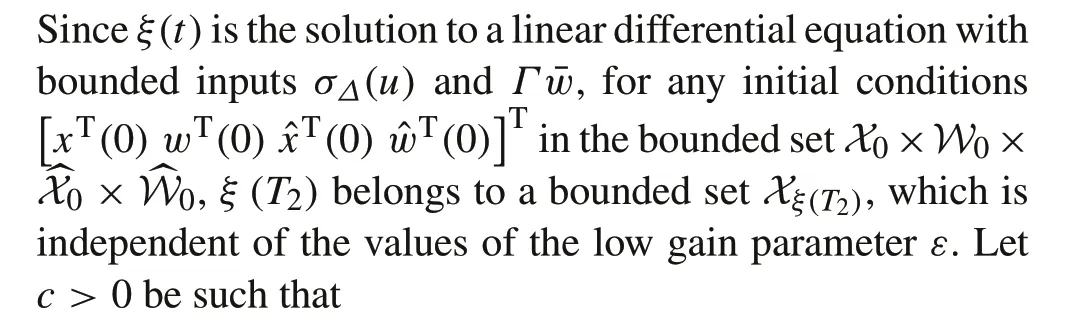
Let
Letε∗∈(0,1]be such that,for allε∈(0,ε∗,
Since limε→0P(ε)=0,suchε∗exists.By Assumption 7,
Thus, we have ‖u‖∞,T2≤Δ, that is,σΔ(u) =u,t≥T2.Thus,Eq.(26)simplifies to
Substituting(27)into(28),we have
By(25)and(29),we have
Evaluating the time difference of the Lyapunov functionValong the trajectories of(30)insideLV(c),we have

Fig.1 The communication topology
that is,
Thus,limt→∞ξ(t)=0.In view of(14),we have
Thus,
This completes the proof.■
5 Simulation
Consider a multi-agent system of three leader agents and five follower agents with the communication topology represented by Fig.1,which satisfies Assumption 1.
The matrices for the dynamics of the leader agents(1)are given by
Assumption 2 holds since all eigenvalues ofSk,k∈I[1,3],are on the unit circle.For eachk∈I[1,3],(Sk,Qk)is observable and,hence,Assumption 4 is satisfied.
Let
and the weightings for the leader agent outputs be chosen asα1=0.2,α2=0.3 andα3=0.5.
The dynamics of the follower agents are described by(2).The system matrices for follower agentsvi,i= 4,5, are given by
The system matrices for the follower agentsvi,i= 6,7,8,are given by
All eigenvalues ofAi,i∈I[4,8], are on the unit circle,(Ai,Bi)is stabilizable and(Ai,Ci)is detectable.Thus,Assumptions 3 and 5 are satisfied.LetΔ=8.
Fori=4,5,we have
and fori=6,7,8,we have
which solve(5).It can be verified that Assumptions 6 and 7 are satisfied,withδ=0.1 andT=0.
In the following two subsections, we present simulation results for the state feedback and the output feedback,respectively.For simulation,we set
and
5.1 State feedback case
The Laplacian matrix of the communication topology among the follower agents is calculated as
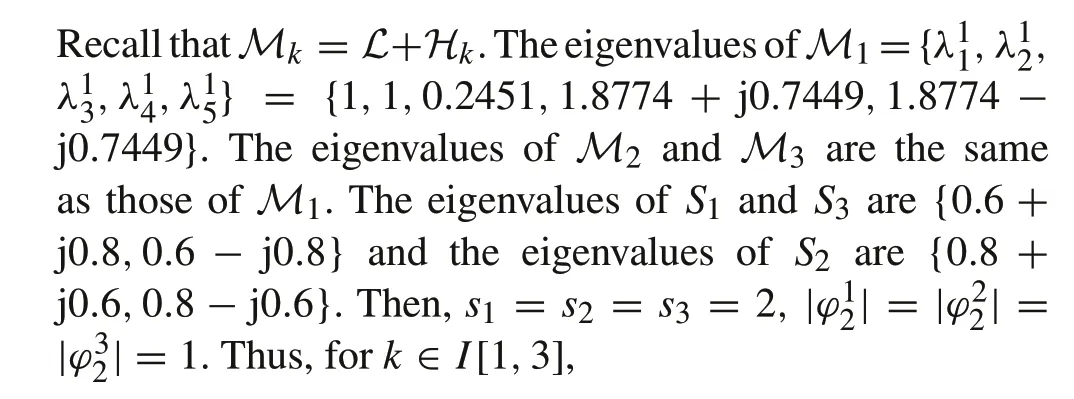
Thus,μk,k∈I[1,3],can all be chosen as 0.5.
Let the initial conditions of the observers(6)be given by
Shown in Fig.2 are the states of the observers(6).For eachk∈I[1,3], the states of the observers ˆwik(t),i∈I[4,8],converge to the stateswk(t)of the leader agentsvk.
We first letε= 0.1 in the control protocols (10).The solutions of the corresponding AREs(4)are
Fori=4,5,Υi=[0.2940 0.9842 1.4509].Fori=6,7,8,Υi= [0.0301 0.5115 3.1577].Figure3 shows that the tracking errorseikfail to converge to 0 and Fig.4 shows that the outputs of the follower agents fail to track the signal¯z.
We next choose a smaller value ofε= 0.01.With this,the solutions to AREs(4)are
Fori=4,5,Υi=[0.0954 0.4411 0.9507].Fori=6,7,8,Υi= [0.0226 0.4061 2.7085].Figure5 shows that the tracking errors converge to 0 and Fig.6 shows that the outputs of the follower agents track the signal ¯z.
5.2 Output feedback case
Following the development in Sect.4, we design two types of leader state observers (7) and (8).The gain matrices for observers(7)are given by
which are such thatSk+Lk Qk,k∈I[1,3],are Schur.We next determine the parameterτkin observers(8).We calculateL133,L233andL333as follows:
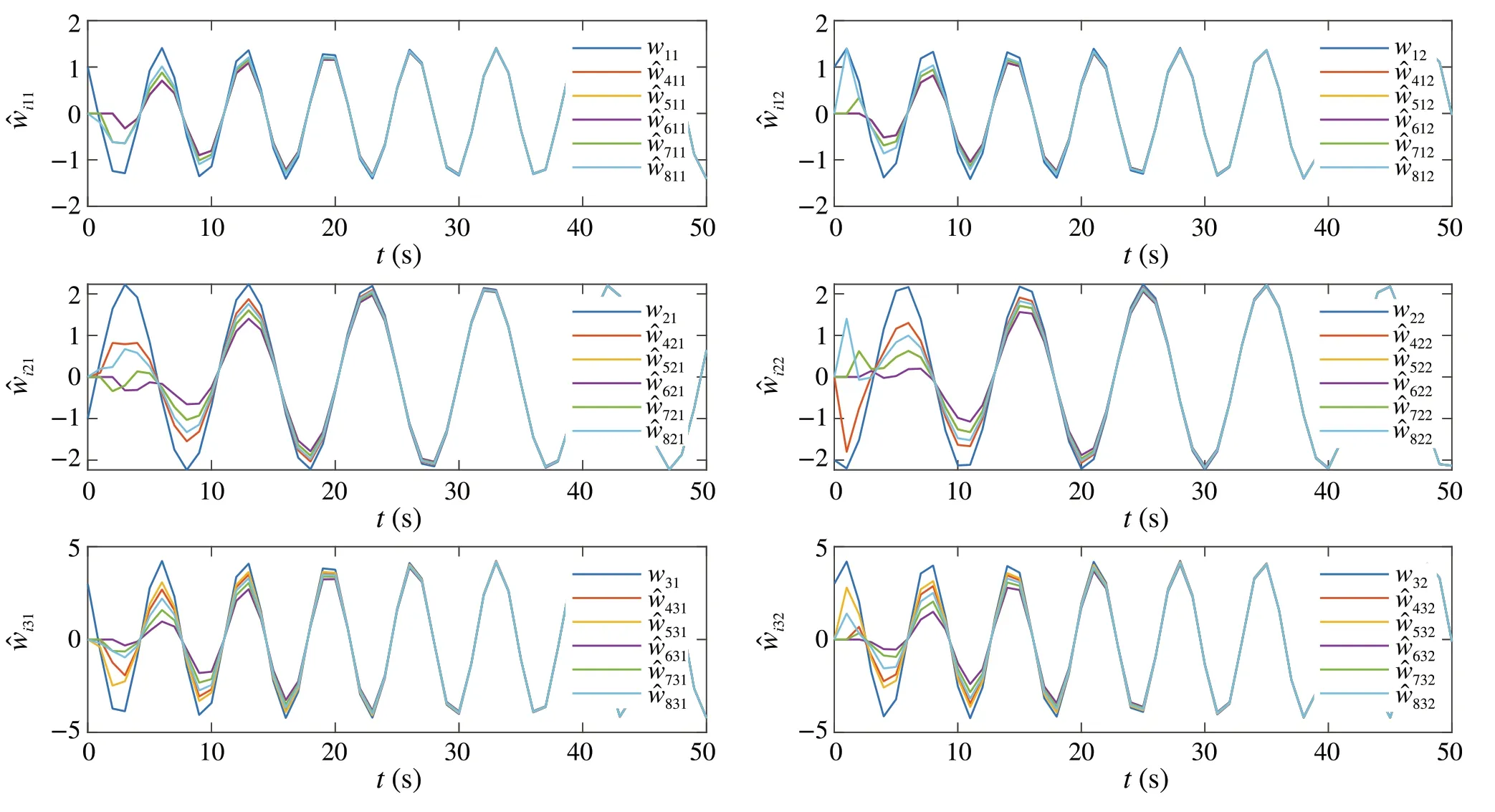
Fig.2 The states wk =[wk1 wk2]T,k ∈I[1,3],of the leader agents and their estimates ˆwik =[ˆwik1 ˆwik2]T,i ∈I[4,8],by the observers(6)
The eigenvalues ofLk33,k∈I[1,3], are all 1.Thus, by Lemma 4,
in view of which we chooseτk=0.5.In the state observers(9),for follower agentsvi,i=4,5,we choose
and,for follower agentsvi,i=6,7,8,we choose
This choice ofL X,iguarantees thatAi-L X,iCi,i∈I[4,8],are all Schur.The initial states of the observers (7)–(9) are selected as
Shown in Fig.7 are the states of the observers (7) and(8).For eachk∈I[1,3],the states of the observers ˆwik(t),i∈I[4,8],converge to the stateswk(t)of the leader agentsvk.
We first chooseε= 0.1 in (18).The solutions to the corresponding AREs (4) and the feedback gainΥiare as given in Sect.5.1.Figure8 shows that the tracking errorseikfail to converge to 0 and Fig.9 shows that the outputs of the follower agents fail to track the signal ¯z.
We next choose a smaller valueε= 0.01.The solutions to the corresponding AREs(4)and the feedback gainΥiare as given in Sect.5.1.Figure10 shows that the tracking errorseikconverge to 0 and Fig.11 illustrates that the outputs of the follower agents can track the signal ¯z.
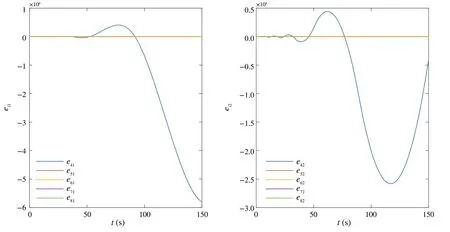
Fig.3 The tracking errors ei =[ei1 ei2]T,i ∈I[4,8],under the state feedback control protocols(10)with ε =0.1
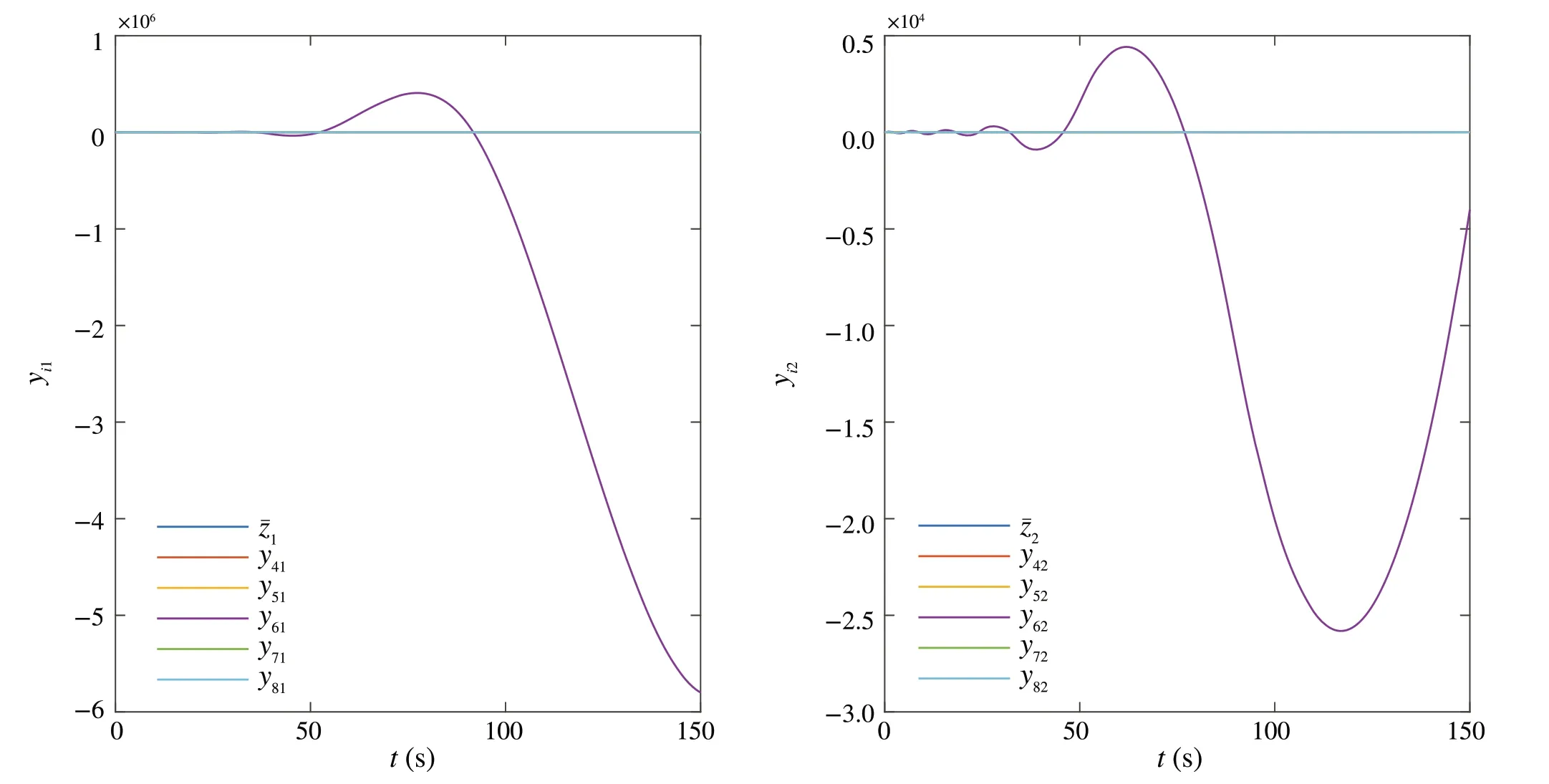
Fig.4 The outputs yi = [yi1 yi2]T, i ∈I[4,8], of the follower agents and the reference signal ¯z = [¯z1 ¯z2]T under the state feedback control protocols(10)with ε =0.1

Fig.5 The tracking errors ei =[ei1 ei2]T,i ∈I[4,8],under the state feedback control protocols(10)with ε =0.01
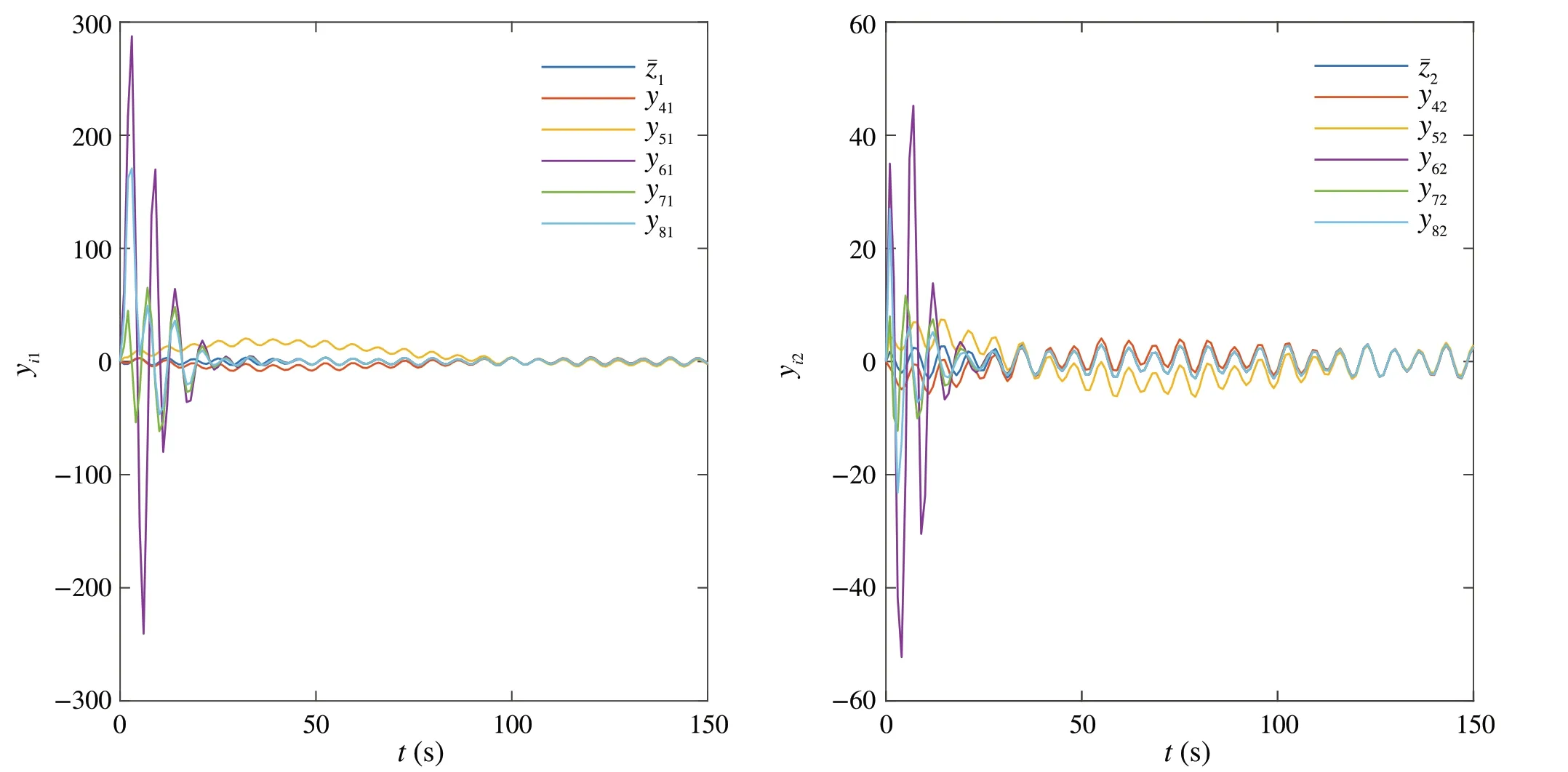
Fig.6 The outputs yi = [yi1 yi2]T, i ∈I[4,8], of the follower agents and the reference signal ¯z = [¯z1 ¯z2]T under the state feedback control protocols(10)with ε =0.01

Fig.7 The states wk =[wk1 wk2]T,k ∈I[1,3],of the leader agents and their estimates ˆwik =[ˆwik1 ˆwik2]T,i ∈I[4,8],by the observers(7)and(8)

Fig.8 The tracking errors ei =[ei1 ei2]T,i ∈I[4,8],under the output feedback control protocols(18)with ε =0.1
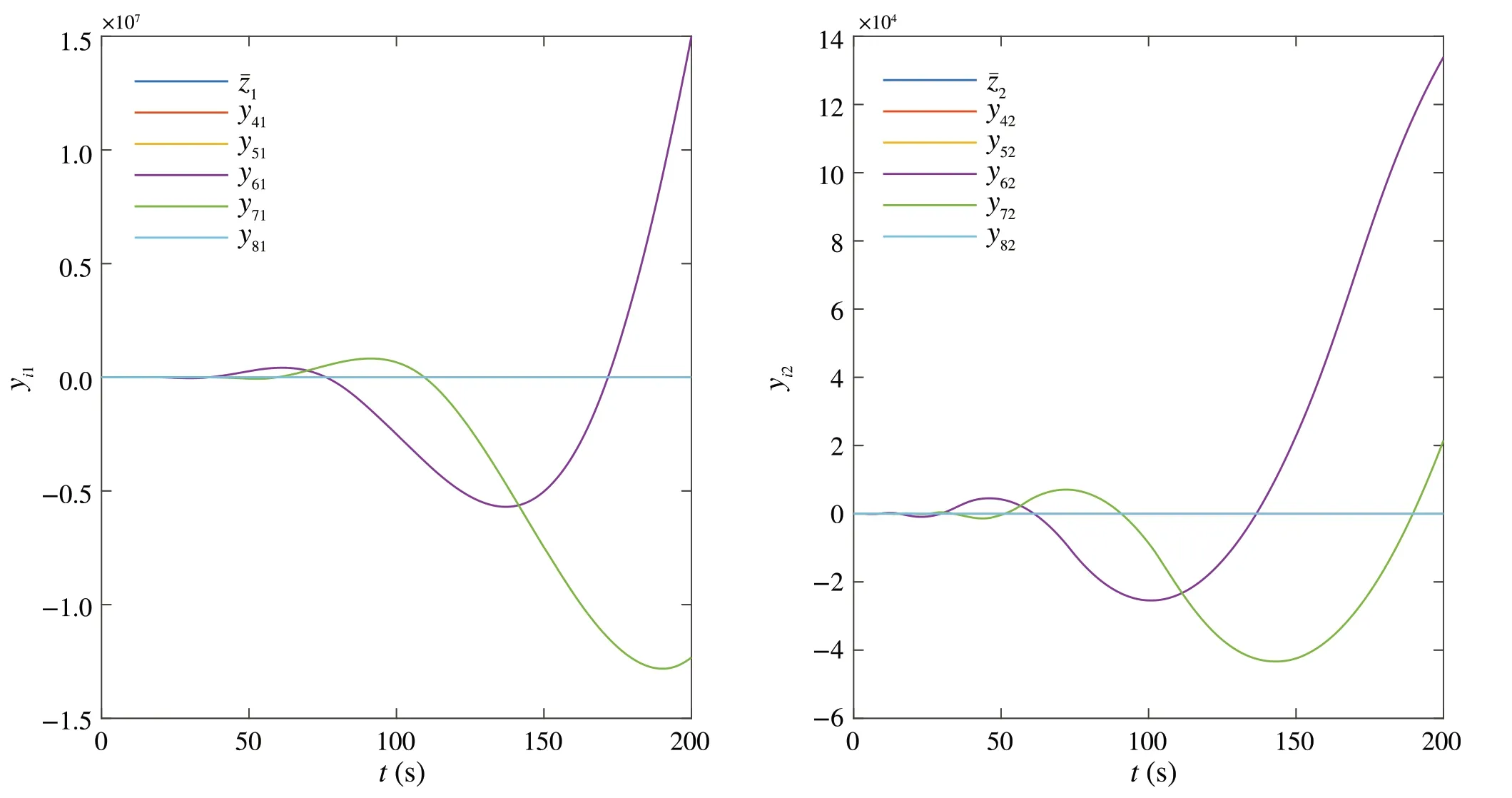
Fig.9 The outputs yi = [yi1 yi2]T,i ∈I[4,8],of the follower agents and the reference signal ¯z = [¯z1 ¯z2]T under the output feedback control protocols(18)with ε =0.1

Fig.10 The tracking errors ei =[ei1 ei2]T,i ∈I[4,8],under the output feedback control protocols(18)with ε =0.01
6 Conclusions
We revisited the semi-global weighted output average tracking problem for a discrete-time heterogeneous multi-agent system with input saturation and external disturbances.We assumed the existence of a directed path from each leader agent to each follower agent and designed low gain-based control protocols of both the state feedback and the output feedback types.It was shown that, for anya priorigiven,arbitrarily large,set of initial conditions,these control protocols cause the follower agents to track the weighted average of the outputs of the leader agents as long as the low gain parameter is tuned sufficiently small.
Data availability Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
杂志排行
Control Theory and Technology的其它文章
- Editorial:special issue on frontiers of control and automation,dedicated to Prof.Ben M.Chen 60th birthday
- Feedback control for stochastic finite-time/fixed-time synchronization of stochastic coupled nonlinear systems
- Sliding mode-based adaptive tube model predictive control for robotic manipulators with model uncertainty and state constraints
- Contracted product of hypermatrices via STP of matrices
- A hybrid data-driven and mechanism-based method for vehicle trajectory prediction
- Input-to-state stability and gain computation for networked control systems
