Input-to-state stability and gain computation for networked control systems

Qianqian Cai·Minyue Fu

Abstract This paper studies the stability problem for networked control systems.A general result, called network gain theorem, is introduced to determine the input-to-state stability (ISS) for interconnected nonlinear systems.We show how this result generalises the previously known small gain theorem and cyclic small gain theorem for ISS.For the case of linear networked systems, a complete characterisation of the stability condition is provided, together with two distributed algorithms for computing the network gain: the classical Jacobi iterations and a message-passing algorithm.For the case of nonlinear networked systems,characterisation of the ISS condition can be done using M-functions,and Jacobi iterations can be used to compute the network gain.

Keywords Small gain theorem·Networked systems·Input-to-state stability·Robust stability·Distributed algorithm

1 Introduction

The celebrated gain theorem is a pivotal tool in stability analysis and control design for nonlinear systems.This tool was initially introduced by Zames for linear feedback gains[1],but then widely extended to various types of nonlinear and uncertain systems[2–4].Many versions of the small gain theorem are available for input–output stability, input-to-state stability[5],nonlinear feedback design[6,7],just to name a few.A good review of the small gain theorem can be found in[8].

This paper is interested in generalising the small gain theorem to networked control systems.Our work is inspired by thecyclic small gain theoremin[9]which provides a simple stability test for networked systems with a max-type gains for all the simple loops in the network.The aim of this paper is to study stability conditions for more general gain functions and study computational algorithms for testing network stability.Our work is also closely related to (1)thematrix small gain theoremof [10] where the network stability is assessed using a matrix of local gain functions,and(2)our recent work[11]where a unified framework is provided for network stability analysis under three notions of stability,namely global uniform boundedness,global asymptotic stability and input-to-state stability.In particular, [11] checks the network stability in terms of a scalar called the network gain.The result,callednetwork gain theorem,generalises the previously known matrix small gain theorem and cyclic small gain theorem for input-to-state stability (ISS).To make the computation of the network gain feasible,[11]also provides a characterisation of the network gain in terms of a discretetime system, which then allows the numerical computation of the network gain.

The motivation of this paper stems from the fact that the results in[11]are for general networked systems;hence,their theoretical development and test algorithms are highly technically involved.In particular,the proof of the network gain theorem in[11]employs the tool of vector-valued Lyapunov functions.Moreover, a lot of the technical development in[11] is devoted to study the families of nonlinear networks rather than a single nonlinear network, so that the network stability conditions become necessary and sufficient.

In this paper,we first restate the network gain theorem in[11]and gives an very intuitive proof sketch to reveal the key ideas in the proof.This will help to understand the network gain theorem much better.We then give a new and intuitive proof for the cyclic small gain theorem.The highlight of the paper will be on the computation of the network gain.For a linear network,we first give a necessary and sufficient boundedness condition for the network gain and show that this condition cannot be reduced to a cyclic small gain condition.This will be followed by two distributed computation algorithms, one based on Jacobi iterations and one using a message-passing algorithm.Distributed computation allows the stability to be assessed for a large networked system without central computation facilities or centralised knowledge of the whole network.Finally,we consider the nonlinear network case and suggest the use of Jacobi to test the network gain.

The rest of the paper is organised as follows.This section will end with some notations and definitions.Section 2 reviews the well-known single-loop small gain theorem in the ISS setting.Section 3 formulates the network stability problem.Section 4 revisits the network gain theorem in[11]and studies some special cases, including the cyclic small gain theorem.Section 5 devotes to the network gain computation for linear networks,whereas Sect.6 comments on the nonlinear network case.Conclusions are reached in Sect.7.

Notations and definitions R is the real field and R+is the non-negative part of R.col{x1,x2,...,xn}denotes a column vector ofxi.ρ(A) stands for the spectral radius of matrixA.|·|stands for the Euclidean norm and|·|∞stands for the maximum norm.Id denotes the identity function.For any measurable functionu: R+→Rm, ‖u‖ denotes ess.sup.{|u(t)|,t≥0}and,for any 0 ≤t1 0 for allx/= 0, and isproper(orradially unbounded)ifV(x)→∞as|x|→∞.A functionγ: R+→R+is said to be of classKif it is continuous and increasing withγ(0)=0.Suchγis of classK∞if it is also proper.A functionβ: R+×R+→R+is said to be of classKLif,for each fixedt∈R+,the functionβ(·,t) of classKand, for each fixeds∈R+, the functionβ(s,·)is non-increasing withβ(s,t) →0 ast→∞.Note that for any functionγof classK∞,its inverse functionγ-1is well defined and is also of classK∞.

Consider the following system:

withx∈Rnis the state,u∈Rmis the input,y∈Rpis the output,andfandhare smooth functions.The system is said to beinput-to-output stable(IOS) if there exists a functionβof classKLand a functionγof classKsuch that, for eachx(0),each measurable essentially boundeduand eachtin the right-maximally defined interval of the solution of(1)–(2),it holds

In this case,γis said to be theinput-to-output gain(or simplygain).Ifyabove becomesx,the system is said to beinputto-state stable(ISS)andγis theinput-to-state gain.

2 Single-loop small gain theorem

The well-celebratedsmall gain theoremhas many forms.Here,we review one of the general forms developed in[5],expressed using Lyapunov functions.Consider the following interconnected system:

where,fori,j=1,2,j/=i,xi∈Rniis the state,ui∈Rmiis the input,yi∈Rpiis the output, andfi,hiare locally Lipschitz functions satisfyingfi(0,0,0)=0 andhi(0)=0.A special output is the state,i.e.yi=xi.The system block diagram is depicted in Fig.1a, whereG1andG2represent the two subsystems,and the ⊕symbol can be interpreted as theaugmentation operator,i.e.u1⊕y2=(u1,y2).

Suppose thei-th subsystem of (4)–(5)admits a continuously differentiable ISS-Lyapunov functionVi:Rni→R+satisfying the following conditions:

C1:There existsαi,α¯i∈K∞such that

C2:There exist,γi j∈Kforj/=iand a continuous,positive definiteαi∈K∞such that

Lemma 1Suppose the interconnected system(4)–(5)is such that each i-th subsystem admits an ISS-Lyapunov function Vi satisfying(6)–(7).Then,the interconnected system is ISS if the following small gain condition holds:

i.e.γ12(γ21(s))0.

Fig.1 Small gain theorem:a Block diagram;b Graph Representation

Fig.2 Examples of networked systems

We use the graph representation in Fig.1b to represent the interconnected system(4)–(5).For notational simplicity,variablesui,yi,xiand functionsfi,hi,are suppressed.If necessary,the gainsγi jcan also be suppressed.

3 Problem formulation

We now generalise the single-loop system in Fig.1 to a networked system consisting ofnsubsystems:

wherexi∈Rniis the state,ui∈Rmiis the control,x=col{xi}∈RNwith,andfi:RN+mi→Rniis locally Lipschitz function satisfyingf(0,0)=0.

Denote byG={V,E}theinduced graphof the networked system as depicted in Fig.2,whereV={1,...,N}andEis a directed edge set with(i,j)∈Eindicating thatfidepends onxi.For eachi∈V, denote the set of itsneighboursbyNi= {j:(i,j) ∈E} and its cardinality by |Ni|.Apath p= {i1,i2,...,ir} is a connected sequence of nodes inG, i.e.(i j,i j+1) ∈Efor everyj= 1,2,...,r- 1.Thepath lengthofpabove isr-1.Thedistancebetween two connected nodes is the shortest path length between the two nodes.Thediameterof the graph is the maximum distance between any two connected nodes.Acycle(orloop)is a path withi1=ir.Asimple cycleis a cycle where all the nodes are distinct except for the starting and terminating node.

The following powerful result,called thecyclic small gain theorem,is cited from[8].

Lemma 2Suppose the networked system(9)is such that each i-th subsystem admits a continuously differentiable ISSLyapunov function Vi: Rni→R+satisfying C1 and C2′:There exist γi j∈K for every j∈Ni and γui∈K and a continuous,positive definite αi∈K∞such that

Then,the interconnected system is ISS if the following cyclic small gain condition is satisfied:The loop gain for every simple cycle l=(i0,i1,...,ir,i0),as defined by

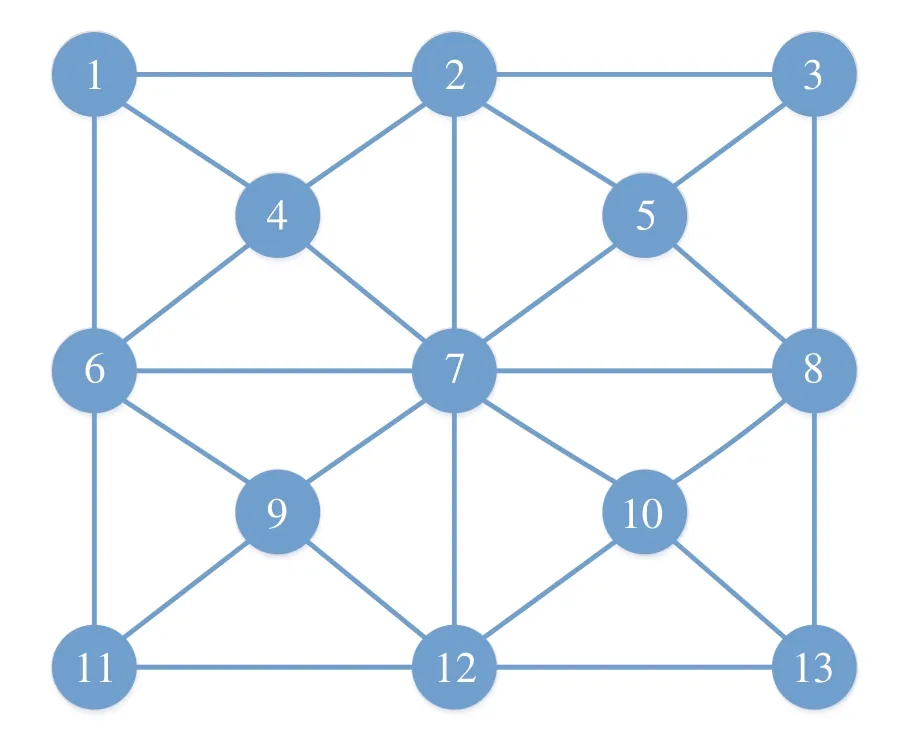
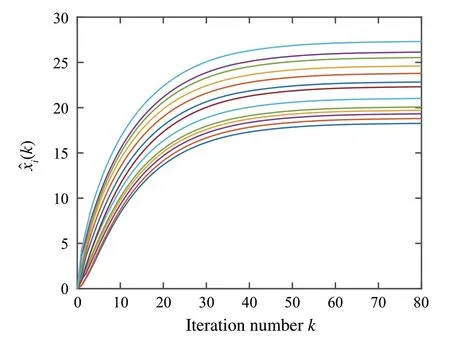
is contractive,i.e.γl

The motivation for this work stems from the fact that the cyclic small gain theorem above is suitable only for the special form of Lyapunov function bound in (10), i.e.maxj∈Ni γi j(Vj) is used to boundVi.This means that thei-th subsystem is influenced only by the neighbouring subsystemj∈Niwith the largestVj,not by all the neighbours.This implies that,if there are multiple loops start and return to nodei,the“compound”loop gain is dominated by the only loop with the largest loop gain.This observation leads to the interesting cyclic small gain condition above.However,for most linear and nonlinear systems,each subsystem is influenced by all the neighbouring nodes, not just one of them.Our interest in this work is to study this more general scenario.As we will see,stability for such networked systems becomes far more complex.

More precisely,we consider the networked system(9)satisfying C1 and C2′′: For everyi-th subsystem, there exists functionγi:,which is continuous and non-decreasing in every variable,γi(0)=0,andαias in C2′such that

The network gain problem we aim to solve consists of determining whether the networked system(9)is ISS or not(thenetwork stability problem)and computing a bound forV(x)for the givenu(thenetwork gain computation problem).

4 Network gain theorem for ISS

In this section,we provide our first main result which characterises the conditions for network stability.

4.1 Network gain theorem

For anyμ∈Rn+,define thestate bounding set

z= col{z1,z2,...,zn} andF= col{F1,F2,...,Fn} (the dependance onμsuppressed for convenience).Then,define

Note in particular thatZμis non-empty because 0 ∈Zμ.

The next result is a generalisation of the small gain theorem, which we will callnetwork gain theorem; see more details in[11].

Theorem 1Under C1 and C2′′,the networked system(9)is ISS stable if Zμ in(14)is bounded for every μ≥0.In this case,the network state(in the steady state)is bounded with F(V(x)) ≤0.Conversely,if Zμ is not bounded for some μ≥0,then there exists some networked system of the form(9)that satisfies C1 and C2′′but is not ISS.

A rigorous proof can be found in [11].In the following,we provide a proof sketch which conveys the key ideas.

ProofThe first part follows from standard stability analysis of nonlinear systems [4].More precisely, C2′′implies that ifVi(xi) ≥γi(Vj(x j) :j∈Ni,‖ui‖), then dVi(xi)/dt≤-αi(Vi(xi)).This in turn implies that the steady statexmust be such that

Hence, the steady stateV(x) = col{Vi(xi)} must be inside the setZμwithμ=col{‖ui‖},i.e.F(V(x))≤0.SinceZμis bounded for any bounded ‖u‖, the networked system is ISS.

Conversely,supposeZμis not bounded for someμ≥0.Weshowbelowthat thereexists amodifiednetworkedsystem of the form of (9) that satisfy C1 and C2′′such that each subsystem remains ISS after modification,but the modified networked system is not ISS.Indeed,the modification of(9)is done by taking

We first claim that every modified subsystemiabove remains ISS.Indeed, letx j= 0 for allj∈Ni.IfVi(xi)>γi(0,‖ui‖), then ˜fi(xi,ui) =fi(xi,ui), resulting in dVi(xi)/dt≤-αi(Vi(xi))by C2′′.This implies that the steady statexiis bounded byVi(xi) ≤γi(0,‖ui‖), so the modified subsystemiremains ISS.

Now,for the modified networked system above,we takex(0)and a constantusuch that‖ui‖=μiandVi(xi(0))=zifor alli,wherez∈Zμis chosen such that|z|∞≥ηfor any given constantη>0.This implies that

which in turn means that ˜fi(x,ui) = 0 att= 0, resulting inxi(t) =xi(0) andVi(xi(t)) =zifor allt≥0.Since|z|∞=ηandηis arbitrarily large,the above analysis implies that the modified networked system does not have a bounded steady state even when the inputuis bounded.Hence, the modified networked system is not ISS.■

4.2 Special cases

ResultsforsomespecialcasesfollowfromTheorem1.Corollary 1 is essentially the small gain theorem (Lemma 1);Corollary 2 is an extension of Corollary 2.Corollary 3 is the cyclic small gain theorem(Lemma 2).

Corollary 1Suppose Conditions C1 and C2′′hold.Then,for a single-loop system(9)with n= 2,the closed-loop system is ISS stable if the set{s: 0 ≤s≤γ12(γ21(s,μ2),μ1)}is bounded for all μ1,μ2≥0.In particular,this holds if γi are taken as in C2 and the small gain condition(8)holds.

ProofUsing Theorem 1,it suffices to show that(8)implies the boundedness ofZμ= {z:z> 0,z1≤γ12(z2)),z2≤γ21(z1)}.Indeed, for anyz∈Zμ,z1≤γ12(z2) ≤γ12(γ21(z1)).Therefore,z1must be bounded.Hence,z2≤γ21(z1)is bounded too.The implication for the case, whenγitake the form as in C2,is obvious.■

Corollary 2Suppose Conditions C1 and C2′′hold.If the induced graph of the networked system(9)is such that all the cycles are non-touching(i.e.no two cycles share a common node),then the networked system is ISS stable if for any μ∈Rn+,every such cycle l=(i0,i1,...,ir,i0)(which must be a simple cycle),the set{s:0 ≤s≤γi0i1◦...◦γiri0(s)}is bounded for every μ∈Rn+(The dependance on μ is suppressed in the set).

ProofThis is a simple extension of Corollary 1.We first lump all the nodes in a non-touching cycle as a“super node"to result in a graph without cycles.It is obvious that this graph is ISS stable if individual node(or super node)is ISS stable.Then, for each super node (i.e.non-touching cyclel=(i0,i1,...,ir,i0)), we can group nodesi1,...,i0as a super node that the gain for this super node isγi1i2◦...◦γirr0.Then,applying Corollary 1 yields that the non-touching cycle is ISS stable when the loop gain(2)is contractive.■

Corollary 3Suppose Conditions C1 and C2′hold and γi takes the form of(10).Then,the networked system is ISS stable if the cyclic small gain condition in Lemma 2 holds.

ProofBy Theorem 1, it suffices to show that the cyclic small gain condition implies the boundedness ofZμ.To see this, take anyz∈Zμand any nodei0∈V.We havezi0≤γi0i1(zi1), wherei1= arg maxj γi0j(z j).Constructi2,i3,...,in+1in a similar way,we have

The sequence{i0,i1,...,in+1}must include cycles because there are onlynnodes inV.Let{ik,...,ir,ir+1}withir+1=ikbe the first encountered simple cyclel.Then,

Sinceglis contractive,zikmust be bounded.Denoting this bound byηl,we havezik≤ηl.Since there are only a finite number of simple loops,ηmax=maxl ηlis bounded.Denote

It follows that

Since there are a finite number of such sequencess,the maximum above is bounded.Becausei0is any node inV, we conclude that allziare bounded,henceZμis bounded.■

5 Network gain computation:linear gains

In this section,we provide complete solutions to the network gain computation problem for the case,whereFis linear.

5.1 Boundedness condition

For eachi∈V,letγibe such that

wherebi=μiwith> 0,andγi j> 0 for allj∈Ni,or 0 otherwise.Then,F(z)=0 becomes

where the matrixG=I-Γ,Γ= {γi j}with allγii= 0.The following result gives the exact characterisation of the boundedness ofZμ.

Theorem 2For the linear gain case(15)–(16),the state bounding set Zμ is bounded for any μ≥0if and only if ρ(Γ)<1.In this case,the maximal solution z⋆=G-1b.

ProofWhenρ(Γ)< 1,Gis invertible andG-1is nonnegative becauseΓis non-negative and

Next, we show that the boundedness condition in Theorem 2 cannot be simplified to a cyclic small gain condition.

Example 1For the network in Fig.2b,suppose everyγi j=0.9 so that the corresponding gain matrix is given by

There are two simple loopsl1=2 →1 →2 andl2=2 →3 →2, each with loop gain of 0.92= 0.81.However, the spectral radius ofΓis,so the networked system is not stable.The reason is that the two loops are additive for node 2,resulting in a compound loop gain of 0.92×2.

5.2 Jacobi iterations

Now, we consider the network gain computation problem under the assumption ofρ(Γ)< 1 and a given boundedu.For a small network,it is easy to computez⋆=G-1b.Here,we consider a large network and study distributed algorithms for computingz⋆.

Thedistributedcomputationproblemisformallydescribed as follows:Devise a distributed algorithm which runs iteratively on every nodei∈Vto compute an estimatezi(k)in iterationk= 0,1,2,...such thatzi(k) →ziask→∞.The computation ofzi(k) uses data available in nodeiand those exchanged from the neighbouring nodesj∈Ni.

Certainconstraintsneed to be imposed on the algorithm’s complexities of communication,computation and storage to call itdistributed.In this paper,these include:

(i) Local information exchange:Each nodeican exchange information with eachj∈Nionly once per iteration.

(ii) Local computation: Each nodei’s computational load(measured in terms of the numbers of multiplications and additions)should be at mostO(|Ni|)per iteration.

(iii) Local storage: Each nodei’s storage size should be at mostO(|Ni|)over all iterations.

The well-known Jacobi iterations serve as a simple and effective distributed algorithm[12]:

with any initialz(0) ≥0 (e.g.z(0) = 0), which can be implemented as,for each nodei,

It is easy to verify that the constraints i)–iii)are satisfied.

It is well known thatzi(k) →ask→∞for alliand allbif and only ifρ(R)< 1[12].This means that we can execute the Jacobi iterations without knowinga prioriwhetherρ(Γ)< 1.In practice,ifz(k)become sufficiently large,the iterations can be terminated.

5.3 Message-passing algorithm

A faster distributed algorithm has been proposed in[13]for iterative solutions of linear systems of the formAx=bwith invertible matrixA.This algorithm belongs to the class ofmessage-passing algorithms,and is known to produce an estimatex(k)in iterationkwith the asymptotic convergence property ofx(k) →∞ask→∞whenAis generalised diagonally dominant.The convergence rate of the algorithm above has also been studied in detail in [14].In particular,the algorithm converges faster than the Jacobi iterations.

Definition 1 A matrixA= {ai j} ∈Rn×nisgeneralised diagonally dominantif there is a positived∈Rnsuch that

andAisdiagonally dominantif(21)holds fordi=1,∀i.

Returning to our problem ofGz=b.It is well known that [12],forG=I-Γwithγii= 0 andγi j≥0 for alliandj/=i,Gis generalised diagonally dominant if and only ifρ(Γ)<1.Hence,the message-passing algorithm in[13]is readily applicable to solvingGz=b.The algorithm is detailed below.In each iterationkof the algorithm,each nodeicomputes variablesgi→j(k)andbi→j(k)for each of its neighbouring nodej∈Niand transmit them to nodej.All the nodes execute the same algorithm concurrently.

We have the following result shows the advantages of the message-passing sequence {ˆz(k)} over the Jacobi sequence{z(k)}.

Theorem 3Suppose ρ(Γ)<1.Then,

ProofThe proof heavily depends on the work in[13]where the message-passing algorithm is introduced.The property(i)comes directly from[13].For(ii),a graph without simple loops with length longer than 2 is effectively an acyclic graph if we join the edges(i,j)and(j,i)together as a single edge.For such acyclic graphs, the finite convergence property in(ii)is established also in[13].To see(iii),we note from(17)thatz⋆=

l≥0Γlb.This means

That is,it includes all the paths(of any length)starting from nodei.From(20),we get

where the maximum is taken over all the paths fromitoj(/=i)without cycles.It is clear thatψmaxis finite.Note that every path fromitojcan be rewritten as a concatenation of a(repeated)cycleitoiand a path fromitojwithout cycles.Using this and the fact thatα<1,we obtain from(28)that

Hence,Ψαis bounded.However, this contradicts the fact that,asα→1/ρ(Γ),Gαbecomes singular andΨαbecomes unbounded.This contradiction means that,asα→1/ρ(Γ),→0 ask→∞.

Therefore, ifρ(Γ) ≥1, then either ˜gi(k) ≤0 for somei,kor limk→∞˜gi(k)=0 for somei.■

Remark 1Theorem 3 also shows that the message-passing algorithm can be used as a distributed algorithm to test forρ(Γ)< 1.More specifically, one can set a (very small)thresholdε>0 and if ˜gi(k)<εis detected at someiandk,ρ(Γ)can be regarded to be sufficiently close to 1.The associated network gain will be either too large or unbounded.In contrast, Jacobi iterations may fail to detectρ(Γ) ≥1.Indeed,(19)can be rewritten as

soz(k)can remain bounded even whenρ(Γ)≥1 ifz(0)andbhappen to be eigenvectors for eigenvalues ofΓless than 1.

5.4 Comparison of algorithms

Example 2To illustrate the Jacobi iterations and messagepassing algorithm, we consider a linear networked system depicted in Fig.3,modified from[13].This is an example of loopy graphs with 13 nodes.The non-zeroγi jis randomly chosen from(0.85, 1) andbi=i.The simulated result

Fig.3 A networked system with 13 nodes

Fig.4 Convergence of the message-passing algorithm

Fig.5 Convergence of the Jacobi iterations

for Algorithm 1 is shown in Fig.4.For 100 iterations, the error is converged down to approximately 0.8×10-4.Figure 5 shows the simulated result for the Jacobi iterations.As we see that the Jacobi iterations converge considerably more slowly,with an error of approximately 0.02 after 100 iterations.From this example,we see that both algorithms work fine,with the tradeoff that Jacobi iterations enjoy simplicity,whereas the message-passing algorithm is more computationally efficient.

6 Network gain computation:nonlinear gains

In this section,we study the network gain computation problem for the case whereFis nonlinear.

6.1 M-functions

The crucial technical issue is how to extend the generalised diagonal dominance condition for the matrixG(or equivalently,ρ(Γ)< 1) to the nonlinear case.Fortunately, a generalised diagonally dominant matrixGwithgii>0 andgi j≤0 is also known as aM-matrix which has a nice nonlinear counterpart calledM-function[15].

Definition 2 A mappingF: D ⊂Rn→Rnisisotone1Isotone functions are also known as monotone functions.(resp.antitone) (on D) ifx≤yfor anyx,y∈D implies thatF(x) ≤F(y) (resp.F(x) ≥F(y)).The mappingFisinverse isotone(on D)ifF(x) ≤F(y)for anyx,y∈D impliesx≤y.Fisoff-diagonally antitoneif for anyx∈Rnthe functions

are antitone.In the above,eiis thei-th unit vector of Rn.

Definition 3 A mappingF: D ⊂Rn→Rnis anMfunctionifFis inverse isotone and off-diagonally antitone.

It is straightforward to verify thatγas in C2′′is isotone andFas in(13)is off-diagonally antitone for anyμ≥0.

6.2 Jacobi iterations

SupposeF: Rn+→Rnas defined in(13)is anM-function for anyμ.Then,for any givenμ,the solutionz⋆ofF(z) =0 can be solved iteratively using the following (nonlinear)Jacobi iterations:

for anyz(0) ≥0.It is well known that limk→∞z(k)→z⋆[15].The distributed implementation is given by

Remark 2In the general case whereFis not necessarily anM-function,computing the network gain can be much more involved.In particular,F(z) = 0 may not exhibit a unique fixedpoint,andtheJacobiiterations(31)mayleadtodifferent fixed points, depending on the initialz(0).To get around this difficulty,we note that the stability analysis is to assess whether the Jacobi iterations(31)are bounded for any initialz(0),rather than to compute the fixed points.This motivates modified iterative algorithms which seek for an upper bound of the asymptoticz(k)only.Such an algorithm is provided in[11].Several simulation examples are also provided in[11].Due to space limit,we do not study this type of algorithms in this paper.

7 Conclusions

A number of results have been presented for determining the input-to-state stability of a networked control system and for computing the input-to-state gains.The network gain theorem (Theorem 1) gives a general characterisation for the network gains (γi) that guarantee the ISS of the networked system.This characterisation is done using the state bounding setZμ.

For the case the network gains are linear,Theorem 2 shows that ISS of the networked system is equivalent to the stability of gain matrix,i.e.ρ(Γ)<1.The classical Jacobi iterations andthemessage-passingalgorithm(Algorithm1)canbeused to compute the input-to-state gains in a distributed way.The message-passing algorithm appears to be a little more complex,but it offers several advantages(Theorem 3),including faster convergence than the Jacobi iterations.

For the case of nonlinear gains,characterisation of the ISS condition can be done usingM-functions,and Jacobi iterations can still be used as a distributed algorithm to compute the input-to-state gains.

Funding This work was supported in part by the National Natural Science Foundation of China(Nos.U21A20476,U1911401,U22A20221,62273100,62073090).