State observers of quasi-reversible discrete-time switched linear systems

Zhendong Sun·Qiang Zhang

Abstract This work addresses observer design for the general class of quasi-reversible discrete-time switched linear systems.Under the mild assumption that the switched system is observable,we present constructive approaches to design state observers to estimate the state.Two types of observers are designed:one is with full order and the other is with reduced order,both could reconstruct the system state in finite times.A numerical example is presented to illustrate the effectiveness of the proposed approaches.

Keywords Switched linear systems·Observer·Observability

1 Introduction

A linear switched system consists of a set of linear subsystems and a switching signal that coordinates the switching among the subsystems.The state of the subsystems is continuous in nature, while the state of the switching signal is discrete/logic in nature.The interaction between continuous state and logic state is an appealing topic that attracts numerousattention[1,2].Asafundamentalclassofhybridsystems,switched linear systems are powerful in both representability and control ability.Interested readers are referred to the monographs[3–5]for progress of switched and hybrid systems.

For a switched linear system, the major topics include stability analysis,stabilizing design,and performance optimization.As a dominant approach for addressing stability and stabilizing design, many Lyapunov-like methods have been developed for dealing with switched systems.For example, the well-known multiple Lyapunov function technique[6] and the composite Lyapunov function technique [7]were successfully applied to switched systems.However,it has been revealed that, even for a planar switched linear autonomous system,stabilizability does not imply the existence of a convex Lyapunov function[8].For discrete-time switchedlinearsystems,thedynamicprogrammingapproach provides constructive design for the stabilization problem[9].Other approaches including the automata-driven switching scheme [10] and the dissipativity approach [11] were proposed to investigate stability/stabilizability for specific classes of switched systems.

In many practical scenarios,the system state is not totally available, and we have to design state observers/estimators to reconstruct/approximate the state.It has been revealed that, for switched linear systems, the observer design is dual with the state feedback stabilizing design [1, 12].As the state feedback stabilization problem is still unsolved for general switched linear systems,the observer design is also open.For continuous-time switched linear systems,a hybrid observer with impulse was designed for achieving finite-time reconstruction of the state[13].For reversible discrete-time switched autonomous systems, a switched observer was designed for achieving finite-time reconstruction of the state[14].It is interesting to note that, switched observers were also used for parameter identifying of adaptive control[15]and linear time-varying systems[16].

In this work, we study the observer design problem for the general class of quasi-reversible discrete-time switched linear systems with measured outputs.To estimate the state,two types of observers are proposed: one is of full order and the other is of reduced order.In both observers the gain matrices are explicitly designed such that the state transition matrices of the error systems are deadbeat in finite times.In this way,the initial state is exactly reconstructed for any control input.Compared with the work[14],the current work extends the system framework from reversible autonomous systems to quasi-reversible controlled systems.Besides,this work also designs a reduced-order observer, which has not been addressed in the literature.

2 Preliminaries

Let R be the set of real numbers, and N+be the set of non-negative integers.For positive integerk, letk={0,1,...,k-1}.LetInbe then-dimensional identity matrix.

2.1 System description

In this work, we address the discrete-time switched linear system given by

wherex(t) ∈Rnis the continuous state,σ(t) ∈M={1,2,...,m}is the switching signal,u(t)∈Rqis the control input,y(t)∈Rpis the system output.Ai,Bi,Ci,i∈Mare real constant matrices with compatible dimensions.For convenience,the system is denoted byΣ(Ci,Ai,Bi)M.Without loss of generality,we assume thatt0=0.

Letφ(t;t0,x0,σ,u) be the state of system (1) at timetstarting fromx0att0with switching lawσand control inputu.It is clear that

whereψis the open-loop state transfer matrix

A switching path is a time-driven switching signal defined over a finite-time interval.Suppose thatθis switching path defined overs,then the length ofθis|θ|=s.

2.2 Definitions

Definition 1 Statex0is said to be unobservable if it is indistinguishable from the origin,that is,for any switching signalσand control inputu,we have

The switched system is said to be completely (switched)observable if the unobservable set is{0}.

Definition 2 A state observer for switched system (1) is a dynamical system

wherefis a proper vector function.For a switching signalσ,the observer is said to beσ-asymptotic if limt→+∞(x(t)-z(t)) = 0 for anyx0,z0,andu.When there exists aT>t0such thatx(t)=z(t)for allt≥T,the observer is said to beσ-T-deadbeat.

Definition 3 Theswitchedsystemissaidtobe(output)quasireversible,if

2.3 Assumptions and supporting lemma

Throughout the work,we made the following assumptions:

Assumption 1 Switched system(1)is quasi-reversible.

Assumption 2 Switched system (1) is completely observable.

Remark 1When the switched system is quasi-reversible,the unobservable set is a subspace of the total state space.Furthermore, if the pair(C,A) is quasi-reversible, there is a matrixE∈Rn×psuch thatA+ECis nonsingular.By abuse of notation,we defineC A-1=C(A+EC)-1.Note thatC A-1relies explicitly onE,yet its image space is the same for all possibleE.

Lemma 1Under Assumptions1and2,there is a positive integer,and a switching path θ defined over T,such that the observability matrix

is of full rank.

ProofIt has been established in[17–19]that,for any completely controllable reversible discrete-time switched linear system, the full controllability could be realized through a switching path with less thanswitches.By virtual of the duality between controllability and observability,the lemma follows.■

3 Main results

In this section, we propose two kinds of state observers to estimate the state.The former is in full order,while the latter is in reduced order.Both could exactly reconstruct the state in finite times.

3.1 Full-order observer

Note that the observability matrix in(5)is in nested structure.Without loss of generality, we assume that rankCθ(0)≥1.By searching linearly independent rows from the top to the bottom,we havelblock rows 0=ν1<ν2<···<νl≤Tsuch that

Letik=θ(νk),k=1,...,l,we have indicesκ1,...,κnandj1,...,jlwithj1+···+jl=n,such that the matrix

is square and nonsingular,whereCi,jdenotes thejth row of matrixCi.

DenoteGk=Ψ(νk+1,0,θ),k= 1,...,l-1.Let ˆCikbe the matrix composed by theκth rows ofCik,k=1,...,l.We could re-write matrixQby

Letζibe thej-th column of matrixQ-1.Furthermore,define

To estimate the state,we propose the following observer:

Theorem 1SupposethattheswitchedsystemsatisfiesAssumptions1and2.For any initial state x0and control input u,we have

ProofLet ˜x(t) =x(t) -z(t),t= 0,1,...,T.It can be verified that

As a result,we have

Simple calculation gives

where

Utilizing the fact thatH1is orthogonal to ¯Ci2G1,we have

Continue this process gives

In the same manner,we could calculate that

Therefore,we have

which directly leads toΛ=0.■

3.2 Reduced-order observer

In this section, we propose a reduced-order observer that achieves deadbeat reconstruction of the state.The motivation of introducing reduced-order observers is twofold:(i)compared with a full-order observer, the transient performance of the lower-order observer usually could be improved as the system order is reduced;and(ii)in a reduced-order observer,the switching law design is much simpler with fewer switches in the observation period.

We assume that the output is independent of the switching law,that is,y=CxwithC/=0.

system could be re-written by

where

Lemma 2Under Assumptions1and2,switched systemisquasi-reversibleandcompletelyobservable.

ProofFirst, it is clear thatis quasireversible.

Second,note that the transformed switched system(12)is completely observable.This means that the matrix

is of full rank.As the result,we have

Construct the observer that is the(n-p)th-order switched linear system given by

where

Theorem 2SupposethattheswitchedsystemsatisfiesAssumptions1and2.For any initial state x0and control input u,we have

ProofDefine the error variable

It can be verified that

Thus,the error dynamics is a switched autonomous system.Note the state transition matrix of the error system along switching path ¯θis exactly the left-hand matrix in (13).It follows straightforwardly that Eq.(16)holds true for anyx0andu.■

Remark 3The reduced-order observer could reconstruct the state inυn-psteps.Note thatCompared with the full-order observer, the upper bound of the observation period is smaller.

Remark 4While the design procedure could be extended to more general situation that the output relies on the switching law,there are still some specific cases that are quite involved.For instance,examine the planar switched linear system with

The switched system is completely observable,yet we do not know whether it admits a reduced-order observer or not.

3.3 Numerical example

Let us examine the fifth-order switched linear system with two subsystems,whose system matrices are

It can be easily verified that both Assumptions 1 and 2 are satisfied.

Simple calculation shows that the switching pathθ=(1,2,1,2,1,2,1) is an observability switching path.By applying the design procedure,we have observer gain matrices

Fig.1 Full-order dynamics

The observer is

which could achieve deadbeat reconstruction of the state in 7 steps.Figure 1 depicts the state,observer,and error trajectories with initial statex0= [-1 2 1 -2 1]Tand control inputu(t)=cos(t),t=0,1,2,....

Next, assume that bothx1andx2could be consistently measured, that isC=C1.Let ¯θ=(2,1,2,1,2), and the gain matrices are

The reduced-order observer is

whereL(0)=L(2)=L1,L(4)=L3,andL(1)=L(3)=03×2.This could reconstruct the state in 5 steps.Figure 2 depicts the state, observer, and error trajectories with the same initial state and control input as in Fig.1.It can be seen that the error dynamics is much smaller than that with the full-order observer.

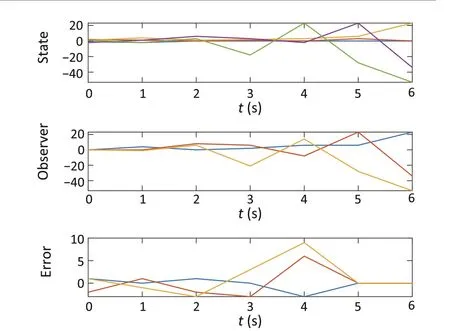
Fig.2 Reduced-order dynamics

4 Conclusion

In this work, the problem of observer design has been addressed for quasi-reversible discrete-time switched linear systems with measured outputs.We proposed two kinds of state observers,and proved that the observers could achieve finite-time reconstruction of the state.

It should be noted that,the observer could achieve exact state reconstruction in a finite time,thus any state feedback control/switching laws could be replaced by observer-driven control/switching laws.However,when the switched system undergoes uncertainty/perturbation, the state estimate will be inexact.In this case, it is an interesting issue to develop observer-driven control/switching laws for achieving stability of the overall system.

Acknowledgements The authors are grateful to the anonymous reviewers for their constructive comments.