参外联合激励下非线性Zener 系统的减振机理研究1)

邢景点 李向红,†,2) 申永军†,

* (石家庄铁道大学数理系,石家庄 050043)

† (石家庄铁道大学机械工程学院,石家庄 050043)

** (石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)

引言

工程实际中的有害振动不仅会影响机械设备的性能和使用寿命,更会给系统的安全与可靠性带来严重威胁[1-2].在船舶工业[3]、铁路运输[4]、航空航天[5]等领域,由于外界复杂动态环境等因素的干扰,振动往往具有非线性特性,导致系统产生丰富且复杂的动力学行为.

采用减振装置来减小有害振动对机械系统的不利影响是振动控制中常用的手段,其中黏弹性材料容易构造且具有较好的耗能性能,被广泛应用于各类隔振、减振系统中[6-7].黏弹性是指材料同时表现出黏性流体和弹性固体特性的性质,弹性材料在拉伸和释放时会缩回其原始位置,而黏性流体在拉动时会保持其伸展形状.黏弹性材料结合了这两种特性,它在受到压力后会恢复到原来的形状,但恢复的速度足够慢,可以抵抗下一个振动周期[8].比较典型的线性黏弹性本构模型有Maxwell 模型、Kelvin 模型和Zener 模型,其中Maxwell 模型由一个弹簧和一个阻尼串联而成,能够较好地表达应力弛豫特性,但不能反映蠕变行为;Kelvin 模型是一个弹簧和一个阻尼并联而成,与Maxwell 模型相比,能很好地表达蠕变行为,但不能反映应力弛豫现象,而具有1.5 自由度的Zener 模型可以更好地表征这两种特性[9],它由一个弹簧并联一个Maxwell 元件组成,该系统具有黏弹性材料的优异特性、构造简单且具有较少的系统参数,在提高系统减振效果方面有着广泛应用.

针对该模型,Brennan 等[10]研究了Zener 系统在自由振动和受迫振动条件下的动力学行为,探究了刚度和阻尼对系统性能的影响.焦小磊等[11]提出了归一化的三参数隔振系统设计方法,并给出了正弦激励以及阶跃激励下三参数隔振系统的时域响应解析形式.为了进一步改善Zener 系统的减振性能,Shi 等[12]建立四参数 Zener 模型,并实验验证了该模型在高频段的减隔振性能得到了改善.Wang 等[13]引入立方刚度,改善了三参数隔振器在谐振频率和高频区域的传递特征.Silva 等[14]发现将非线性立方刚度引入主弹簧或Maxwell 元件的弹簧中都将会使高频段减振性能得到改善.康永刚等[15]提出改进的Zener 模型,更准确地描述黏弹性材料的应力松弛行为;范舒铜等[16]提出新型非线性黏弹性能量阱,发现简谐激励下黏弹性非线性能量阱比传统非线性能量阱的减振效果更优.

多频激励下的机械系统具有广泛的工程背景,在实际工程中,系统在多个频率作用下会产生复杂的振动响应以及丰富的动力学行为[17-20].Yang 等[21]研究了多频激励下非线性时变正齿轮系统的频率响应特性,验证了多频激励的存在会导致不同谐波激励之间的相互作用,显著影响系统的非线性振动特性.Dnailo 等[22]研究了在参数激励和外部激励作用下非线性Mathieu-Duffing 系统稳态响应,验证了二次和三次非线性以及参数放大对扩展采集器应用性能的影响.Asnafi[23]研究了Kelvin-Voigt 黏弹性板在参外联合激励下的混沌行为,表明阻尼、激励振幅和频率将影响系统混沌区域.Yan 等[24]研究了参外联合激励下铁木辛柯梁横向振动问题,发现非线性振动中的周期运动和混沌或准周期运动随着轴向平均速度的增加而交替进行,且激励幅值是影响系统响应的重要参数.Mehrdad 等[25]研究了参数激励频率与外激励频率为2:1 的Duffing 型非线性系统的系统响应,利用变幅法求得系统解析解,证明了系统振动响应的有界性.

不同尺度耦合动力系统通常会呈现出簇发振动的特殊振动形式,即大幅振动的激发态和微幅振动的沉寂态的组合.当系统的激励频率与固有频率存在量级差异时,系统就会呈现出多尺度的特性[26].自Rinzel 等[27]提出快慢分析法以来,针对单频慢变激励系统的簇发振动机制已经得到广泛研究.为了解决不同激励频率之间存在差异而引起的快慢动力学问题,Li 等[28]提出了包络快慢分析法,研究了铂族金属上CO 氧化过程中的簇发振荡及其诱导机理.Han 等[29]根据De Moivre 公式提出了频率截断快慢分析法,解决了频率比为m:n的参外联合激励系统的快慢动力学问题.基于此,更多学者对这类系统展开广泛研究.张晓芳等[30]将参外联合激励引入Lorenz系统,探究了系统在严格共振和非严格共振下的簇发振荡机制.曲子芳等[31]揭示了含双频周期激励的不同尺度Filippov 系统的非光滑簇发振荡模式及分岔机制.

目前,对于机械系统减振的研究大多集中在结构仿真与参数优化,Liu 等[32]研究了不同的阻尼结构对准零刚度隔振器隔振性能的影响,发现硬化阻尼有利于隔振性能的提升.Wang 等[33]通过实验探究了黏弹性阻尼材料性能与温度、频率之间的关系,验证了其对结构振动的抑制作用.Zhang 等[34]提出组合阻尼NES,通过数值模拟与不同NES 在不同脉冲载荷幅值下的减振效果进行对比,发现组合阻尼NES 具有更好的减振性能.此外,万洪林等[35]研究了线性动力吸振器对参数激励下Duffing 系统振动控制机理,发现加入吸振器后系统自治系统平衡点稳定性增强是非自治系统减振的主要原因.

低频振动具有传播距离远,隔离困难等特点,且存在于多个领域,例如航天器的微振动、工程建筑、交通运输等[36].因此,目前除了研究共振情形下的振动控制问题之外,低频隔振减振问题也受到了广泛的关注.Wang 等[37]研究了加入软化硬化(SH)元件的NES 的减振性能,发现该系统可以有效降低低频振动;Zhao 等[38]提出了车辆-准零刚度浮置板轨道耦合动力学模型,应用高静低动非线性刚度特征,进一步优化了浮置板轨道的低频减振效果;Zhang等[39]提出了一种具有可编程准零刚度特性的定制机械超材料,通过曲线梁的特定几何形状实现多个准零刚度工作范围,可用于超低频振动隔离.

加入Maxwell 黏弹性元件通常会使动力系统增加半个自由度,因此会增加系统的复杂性,目前关于此类系统减振机理方面的研究工作较少.基于此,本文研究了参外联合激励下Zener 系统的减振机理,其中参数激励为低频激励.采用包络快慢分析法,将低频激励作为慢变参数,结合非自制系统与自治系统相关性,重点讨论了系统的减振效果、分岔机制、减振机理,为参外联合激励下低频振动机理究提供了新的思路.

1 系统方程与减振效果

1.1 系统方程

具有参数和强迫周期激励的非线性Duffing 系统为

其中m1是系统的等效质量,为系统的等效阻尼,,和 ω1分别是系统参激刚度、振幅和频率,为系统非线性刚度系数,和 ω2分别是系统外激励幅值和频率.系统(1)涉及多个频率的耦合,存在大幅振动.为了减少大幅振动对系统的危害,对系统(1)耦合一个Maxwell元件,变为1.5 自由度非线性Zener 系统,如图1 所示,其中ks是参激刚度和非线性刚度部分,和分别是Maxwell 元件的阻尼和刚度

图1 非线性Zener 模型Fig.1 Nonlinear Zener model

引入变换

系统(1)与系统(2)分别变为如下系统

分别写为如下状态方程

1.2 减振效果

下面研究在参数取k=0.1,b=3,c1=0,ω1=0.01,α=1,F0=0.3,ω2=0.1,c=0.4,k1=0.5时,系统(5)和系统(6)不同的动力学行为.

原系统(5)的振动行为如图2 所示,其中图2(a)是位移时间历程图,图2(b)为相图.可以发现轨线振幅趋于增大,这表明系统处于大幅高频振动的发散状态,同时系统一直呈现激发态振动.

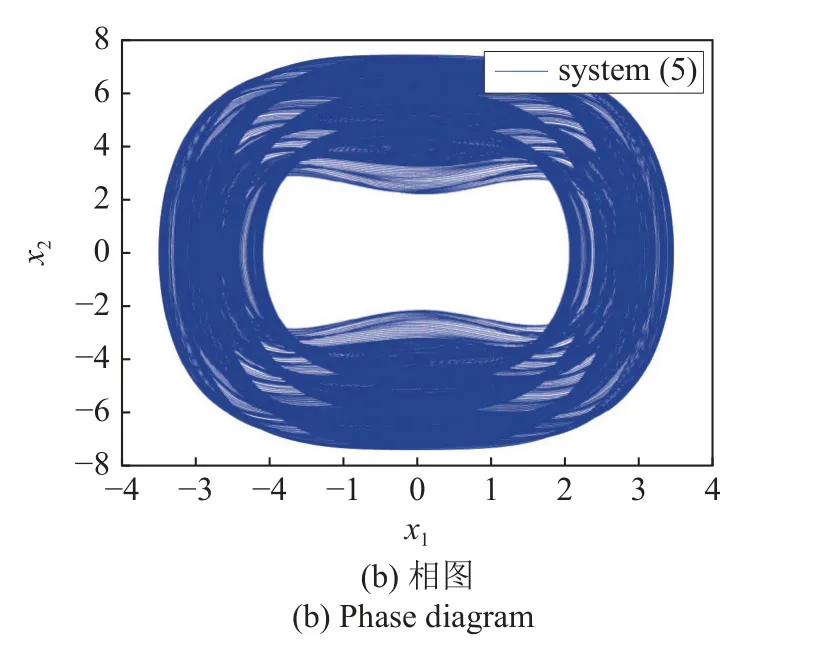
图2 系统(5)振动响应Fig.2 Vibration response of system (5)

耦合Maxwell 元件后,取参数c=0.4,k1=0.5,系统(6)的振动行为如图3 所示.通过对比,发现耦合Maxwell 元件后,系统高频振动大幅降低,出现激发态与沉寂态相结合的混合振动模式,即簇发振动.从两个相图中明显看出,系统位移降低了约50%,速度衰减了近90%.

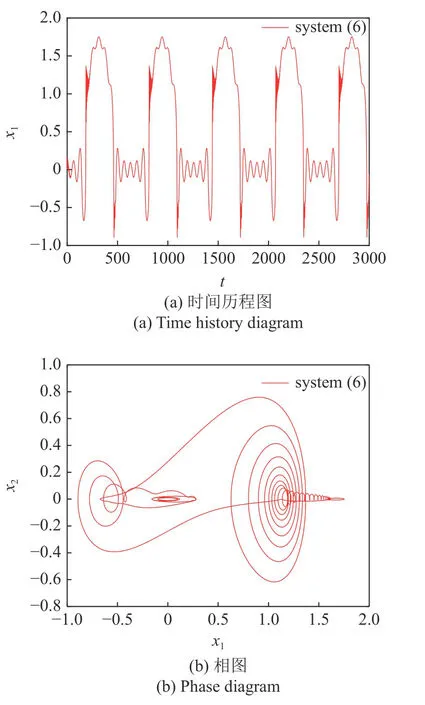
图3 系统(6)振动响应Fig.3 Vibration response of system (6)

2 自治系统的稳定性和分岔分析

下面将深入研究加入Maxwell 元件后系统的减振机理.由于系统中各状态变量的振动行为不但受系统的固有频率的影响,同时又会受到参激和外激的调制,其中参数激励为慢变激励,因此采用快慢动力学中的包络快慢分析法[28]揭示减振机理.令F=bcos(ω1t),当ω1<<1时,在振动周期ϕ 内,取t在[t0,t0+ϕ] 变化,则F在Ft0=bcos(ω1t0)和Ft0+ϕ=bcos[ω1(t0+ϕ)] 内变化,由于ω1很小,使得Ft0与Ft0+ϕ非常接近,所以参数激励F可近似看作常数,为系统的慢变过程,可视为慢子系统,x(t),y(t)为快变量,构成快子系统,则方程式(5)与式(6)都是快慢耦合的非自治系统.再令P=F0cos(ω2t),显然外激励P始终在P1=F0和P2=-F0之间变化.

因此考虑如下自治系统

自治系统(7)和系统(8)与非自治系统(5)和系统(6)的振动密切相关,尤其自治系统的稳定性变化和分岔行为将会对非自治系统的振动产生较大影响.具体而言,自治系统平衡点的稳定性影响着非自治系统振动的收敛和发散趋势;而当自治系统产生分岔行为时,往往会使非自治系统的振动发生变化.此外,分岔参数的周期性变化也会导致自治系统对非自治系统的影响呈现出周期性的变化.

未加入Maxwell 元件自治系统(7)的平衡点为E(x1,0),其中x1为方程 α+(k+F)x1-P=0 的实根,由盛金公式可计算出

自治系统(7)平衡点的稳定性由以下特征方程决定

自治系统(8)的平衡点稳定性由以下特征方程决定

当a0>0,a2>0,a2a1-a0>0 时,平衡点稳定,具体的平衡点类型及稳定性可以通过数值模拟得到.

考虑参数P固定时系统运动状态随参数F的变化情况,当P≠0 时,在临界点右侧,系统有一个平衡点,在临界点左侧,系统有3 个平衡点,系统发生破缺分岔.

下面给出在参数取k=0.1,b=3,c1=0,ω1=0.01,α=1,F0=0.3,ω2=0.1,c=0.4,k1=0.5时,系统(7)和系统(8)分岔图以及平衡点稳定性的变化情况,进一步揭示系统减振机理.

图4 是系统(7)关于参数F的分岔图,其中红线为P=0.3 时的分岔情况,蓝线为P=-0.3 时的分岔情况,整体两组平衡线关于x1=0 对称,且在F=-0.946 9处发生破缺分岔.平衡曲线的稳定性可由式(15)确定,其中平衡线SE1,SF1,SE2,SF2的特征值分别为一对实部为0 的共轭虚根,平衡点类型为中心;平衡线SE3,SF3特征值为一正一负两个实根,平衡点类型为鞍点.图中实线代表稳定的平衡曲线,虚线代表不稳定的平衡曲线.平衡点个数随着F的减小发生变化,P=0.3 时,在分岔点IB1,IB2右侧系统只有一个平衡点,在分岔点左侧系统变为了3 个平衡点;P=-0.3 时在分岔点IB3,IB4右侧系统只有一个平衡点,在分岔点左侧系统变为了3 个平衡点.

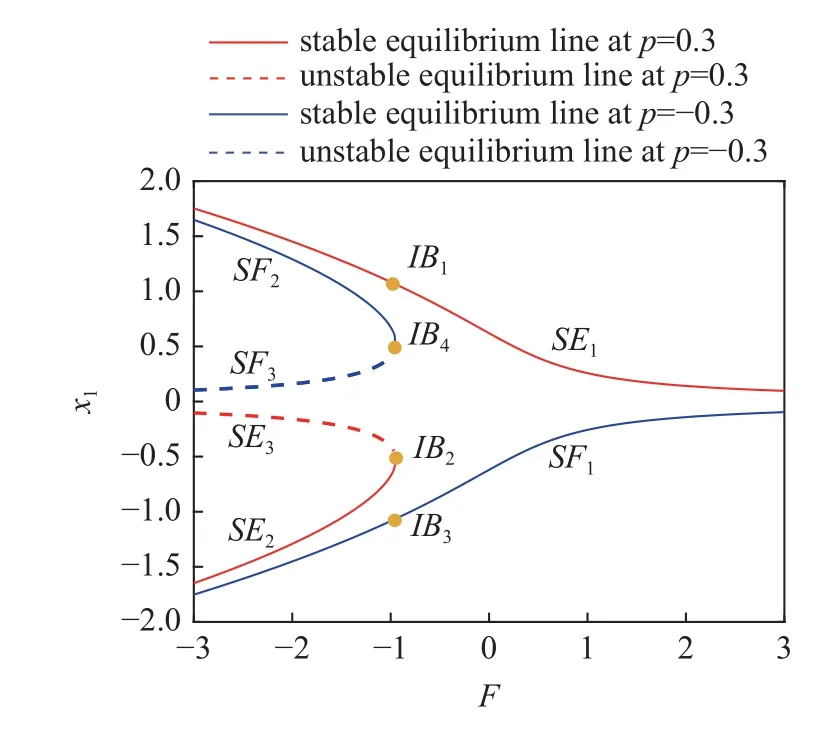
图4 系统(7)关于 F 的分岔图Fig.4 The bifurcation diagram of system (7)with respect to F

加入Maxwell 元件后,系统(8)平衡线的分岔图如图5 所示,由于平衡线方程相同,所以系统(8)平衡点分岔情况形式上与系统(7)一致.其中红线表示P=0.3 时系统的平衡线,蓝线表示P=-0.3 时系统的平衡线,实线代表稳定的平衡曲线,虚线代表不稳定的平衡曲线.平衡线的稳定性可由式(19)确定,每个平衡点有3 个特征根,平衡线SE1,SF1,SE2,SF2特征值分别为一个负实根和一对实部为负的共轭复根,平衡点类型为稳定焦点.平衡线SE3,SF3特征值为一个正实根和一对实部为负的共轭复根,平衡点类型为鞍点.相较于系统(7),虽然都发生了破缺分岔,但平衡线SE1,SE2,SF1,SF2的平衡点类型由中心变为了稳定的焦点.

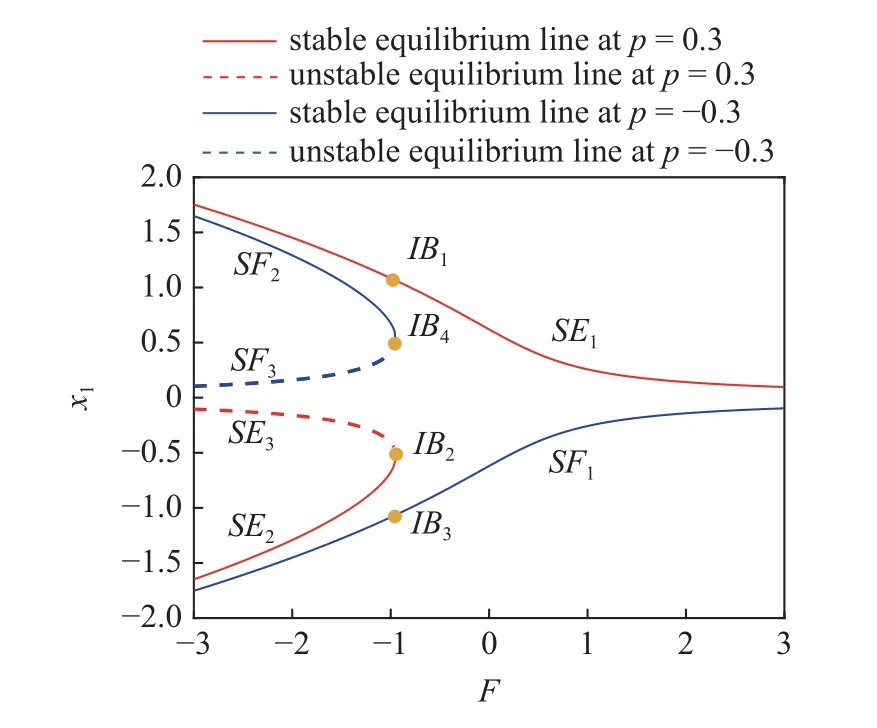
图5 系统(8)关于 F 的分岔图Fig.5 The bifurcation diagram of system (8)with respect to F

3 簇发振动与减振机理分析

为深入理解减振机理,并清楚展示自治系统稳定性与分岔是如何影响该非自治系统的振动行为,采用包络快慢分析和转换相图进行阐述.如图6 所示,将系统(5)在 (F,x1)平面上的转换相图与平衡线分岔图进行叠加,更好地观察在各平衡态附近的轨线性态,可以发现,未加Maxwell 元件的系统由于自治系统的平衡点类型为中心,平衡线对非自治系统轨线的吸引性很弱,因此系统(5)始终呈现大幅振荡现象.

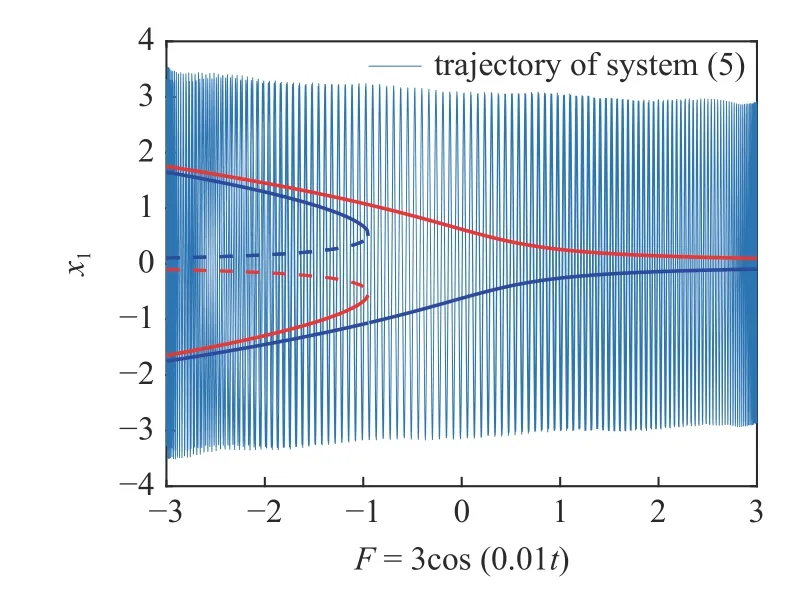
图6 系统(5)转换相图与分岔图叠加Fig.6 The overlap of transformed phase portrait and bifurcation diagram of system (5)

加入Maxwell 元件后,系统轨线在一个振动周期内,存在着明显的簇发现象,如从图7 中可以看出,该周期簇发振动分成4 个部分,SP1-QS1-S P2-QS2,其中SP1,S P2为激发态,QS1,QS2为沉寂态.

图7 系统(6)时间历程图放大图Fig.7 Enlargement of time history diagram of system (6)

下面利用包络快慢分析法揭示振动机理.图8(a)是系统(6)的转换相图,可以看到状态变量x1随慢变参激F=3cos(0.01t)变化而变化的过程.图8(b)是系统(6)转换相图与平衡线分岔图的叠加,随着外激励的值从P1到P2变化,周期性振荡的整个轨迹几乎都包裹在两条平衡线SE1,SF1之间,在破缺分岔点附近,振动轨迹向上偏移,转移到SE1,SF2两条平衡线之间.

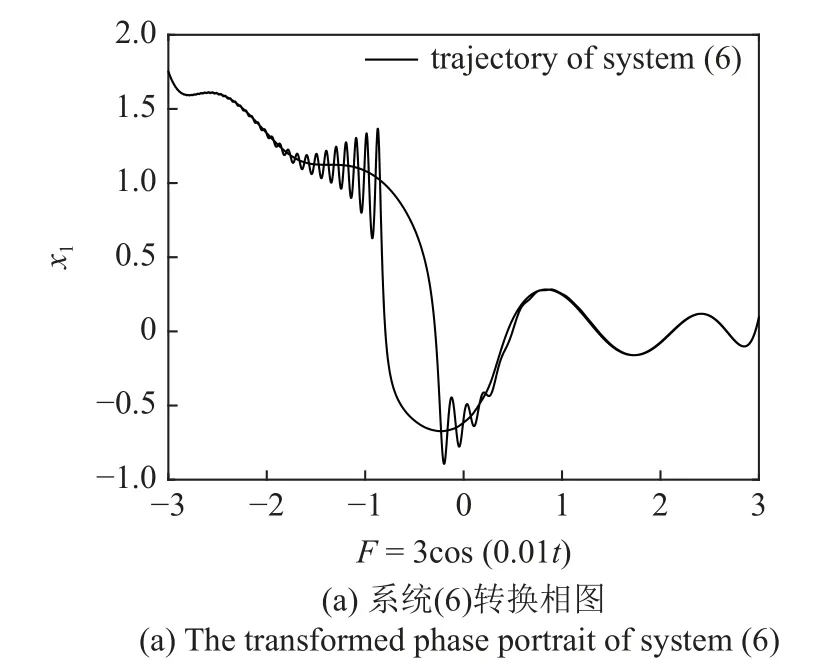
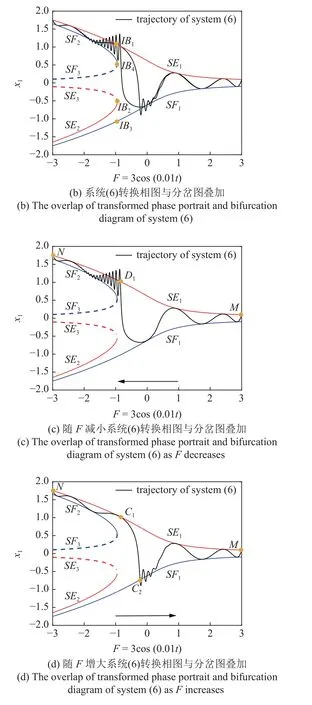
图8 簇发现象产生机理Fig.8 Generation mechanism of bursting phenomenon

为了更清楚观察系统轨线运动状态,将图8 (b)分成两个部分,一部分是随着F减小时的变化情况,另一部分是随着F增加时的变化情况.如图8(c)所示,假设轨线从点M出发,非自治系统(6)受到相应自治系统(8)两条稳定平衡线的吸引,在SE1,SF1之间向左做振荡运动,且轨线始终包裹在两条稳定的平衡线内.当到达点D1后,由于自治系统发生破缺分岔,轨线在平衡线SE1与SF2之间振动,形成了高频振荡的激发态SP1,之后振幅逐渐衰减,直至到达点N附近形成沉寂态QS1.随着时间t的增加,当慢变参数到达极小值F=bcos(ω1t)=-3 时,轨线将会向右折返.如图8(d)所示,轨线从N点出发包裹在稳定平衡线SE1,SF2中向右运动,系统处于沉寂态QS1,当轨线经过破缺分岔点到达点C1后,受到稳定平衡线SF1的吸引,到达点C2,并形成振幅逐渐衰减的激发态SP2,之后很快又进入沉寂态QS2,最终到达点M,至此完成一个周期的运动.同样地,当慢变参数到达极大值F=bcos(ω1t)=3 时,轨线则会折返向左运动,下一个周期轨线会继续在平衡线SE1,SF1,SF2的包裹下做类似的运动.

加入Maxwell 元件后自治系统的平衡点类型发生了改变,SE1,SF1,SF2的稳定性从中心变为稳定的焦点,其吸引性明显增强,由此系统(5)的发散运动变为系统(6)的周期运动,并且振动位移和速度都有显著的减小,系统的大幅振荡得到明显的抑制.此外,破缺分岔使得自治系统多个稳定吸引子共存,从而导致非自治系统轨迹在不同稳定吸引子之间跳跃.因此,在参数激励项为慢变过程时,自治系统的动力学行为对非自治系统的振动具有明显的调控作用.

4 系统参数对减振的影响

破缺分岔会导致系统出现突跳现象,这种现象会导致系统从一个稳定状态跳跃到另一个稳定状态或者在周期运动状态之间切换,使得系统的稳定性受到一定影响[40].根据分岔条件发现可以通过改变系统刚度或者非线性项系数的方式来控制系统破缺分岔的发生,避免出现不稳定平衡点,从而实现对系统的控制和优化.

为了更好地说明这一点,给出了改变系统刚度k和非线性项系数 α 时,系统双参数曲面和分岔曲面的叠加,系统(5)和系统(6)的时间历程图以及系统(8)分岔图和转换相图的叠加,进而展示在不同条件下系统的运动状态,以更好地理解如何通过控制系统参数实现系统优化.

4.1 系统刚度k

改变系统刚度k,其他参数与第3 节取值相同,给出加入Maxwell 元件之后自治系统(8)中x1关于F和k的双参数分岔曲面,如图9(a)所示,其中红色为P=0.3 时双参数分岔曲面,蓝色为P=-0.3时双参数分岔曲面,根据分岔条件计算出k=2.16 是破缺分岔的临界参数值,黄色PE面为破缺分岔临界面.可以看到PE与红色和蓝色曲面发生破缺分岔的临界位置相切,切点在k=2.16 附近,PE面将整个区域分为两个部分,其中红色和蓝色曲面分别在后上方region-1 区域只存在一个平衡点,在前下方region-2 区域有3 个平衡点.在图中关于k取截面,比如k=0.1 时,截面图如图5 所示,取k=3时,截面图如9(b)所示,此时在一定参数范围内系统不存在破缺分岔.

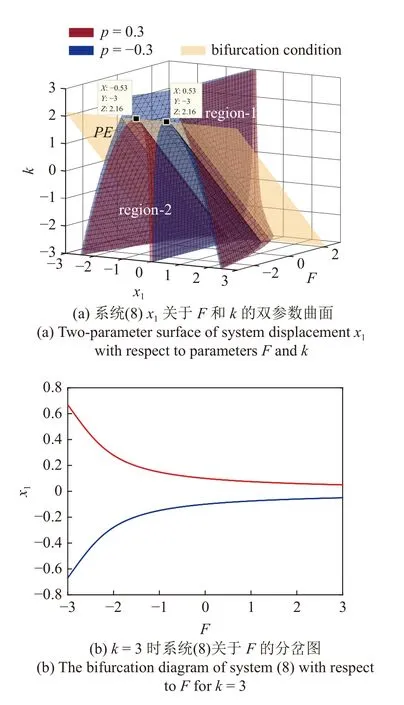
图9 自治系统双参数分岔曲面及在 k=3 时截面图Fig.9 Two-parameter bifurcation surfaces of autonomous systems and cross section atk=3

k=3时,将系统(5)和系统(6)的时间历程图进行对比.如图10 所示,可以看出,系统(5)呈现出明显的大幅振荡现象,并且呈发散趋势.在加入Maxwell元件后,系统呈现微幅高频和大幅低频的混合振动模式,大幅振动得到明显抑制,振动幅值降低到0.7 左右.系统位移降低了近80%,与第一部分k=0.1时发生破缺分岔相比,减振效果得到了明显的提高.其减振机理由图11 给出,可以发现k=3 时,系统(8)不再发生破缺分岔,系统(6)的轨线几乎完全包裹在两条平衡线之间,从而达到减振的效果.

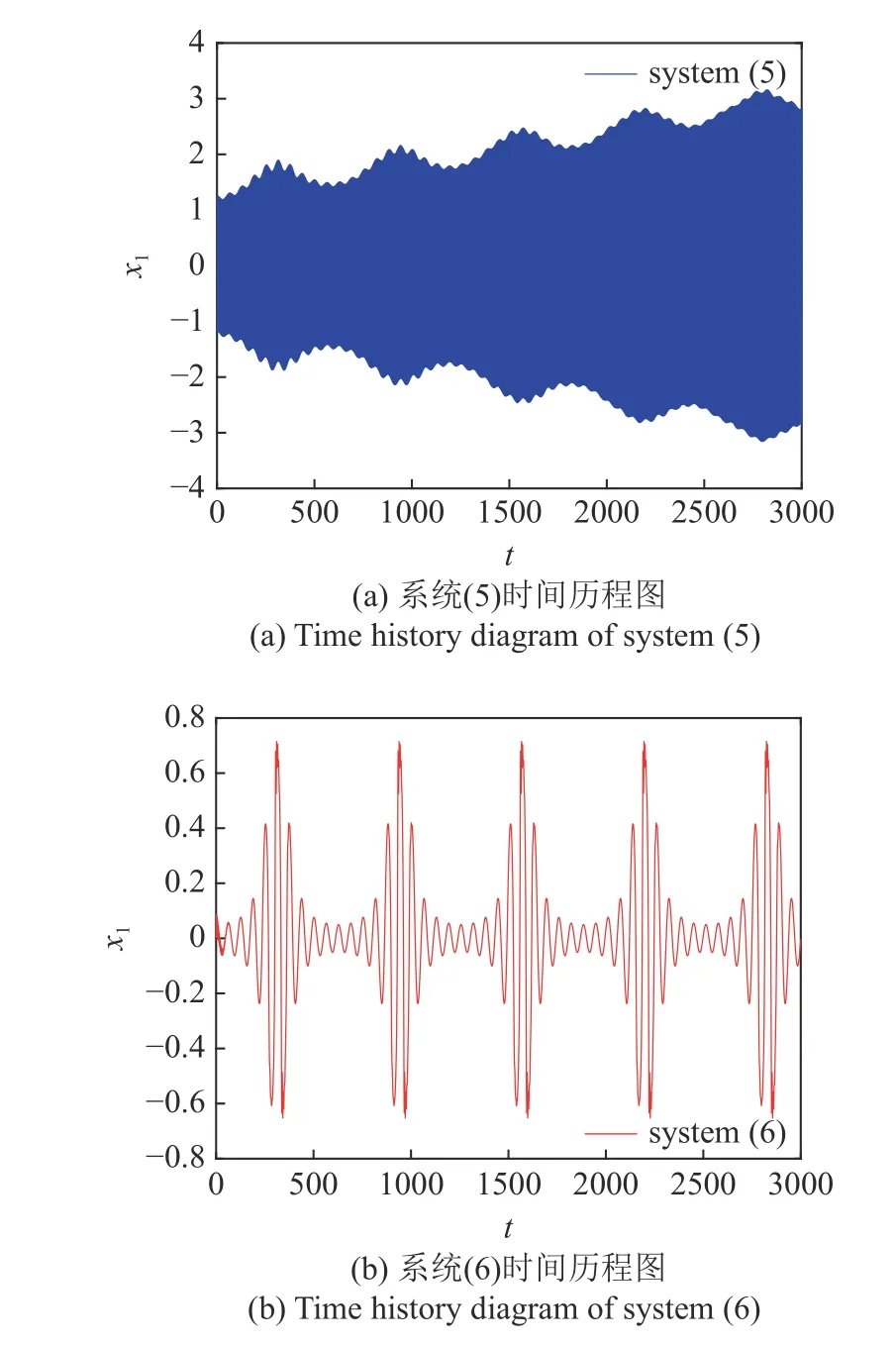
图10 k=3 时系统(5)与系统(6)时间历程图Fig.10 Time history diagram of system (5)and system (6)fork=3

图11 k=3 时系统(6)转换相图与平衡线叠加Fig.11 The overlap of transformed phase portrait and bifurcation diagram of system (6)fork=3

如图12 和图13 所示,给出加入Maxwell 元件前后k=4 和k=10 时的时间历程图,系统均不再发生破缺分岔,且在k=4 时系统位移幅值降低约90%,在k=10 时系统位移幅值降低近99%,即当k≥2.16时,k取值越大,系统减振效果越明显.

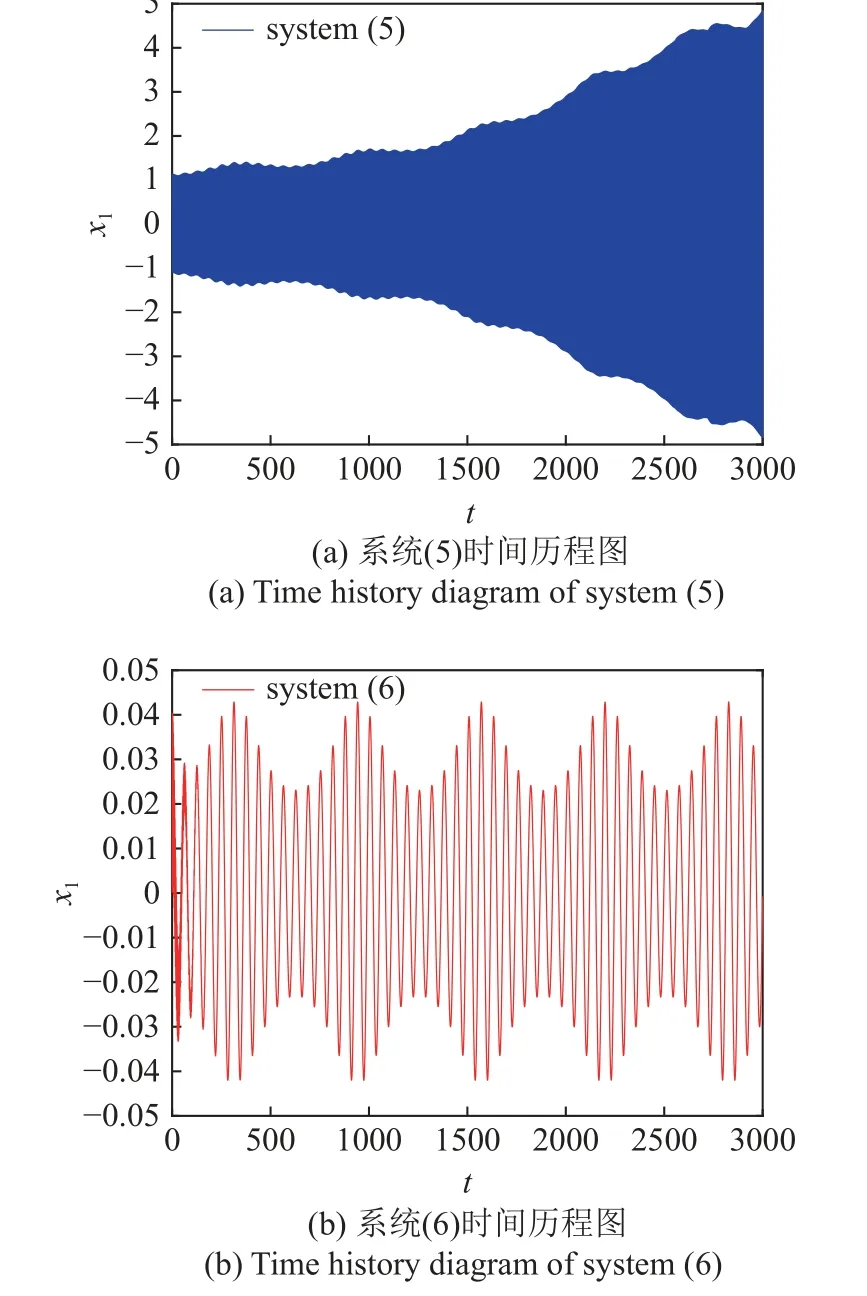
图13 k=10 时系统(5)与系统(6)时间历程图Fig.13 Time history diagram of system (5)and system (6)fork=3

4.2 系统非线性项系数α

参数b,ω1,k,ω2,c,k1,F0与第3 节取值相同,改变系统非线性项系数 α,根据分岔条件计算出大约在 α ≥40.15 时,系统不发生破缺分岔.

如图14 所示,给出自治系统(8)中x1关于F和α的双参数曲面,其中红色为P=0.3 时双参数分岔曲面,蓝色为P=-0.3时双参数分岔曲面,黄色PE面为由分岔条件计算得出的分岔临界面,可以看到PE与红色和蓝色曲面发生破缺分岔的临界位置相切,切点在 α=40.15 附近.PE面将整个区域分为两个部分,其中红色和蓝色曲面分别在后上方region-1 区域只存在一个平衡点,在前下方region-2 区域有3 个平衡点.图中关于 α 取截面,比如 α=1 时,截面图如图5 所示,取 α=40.2 时,截面图如图14(b)所示.

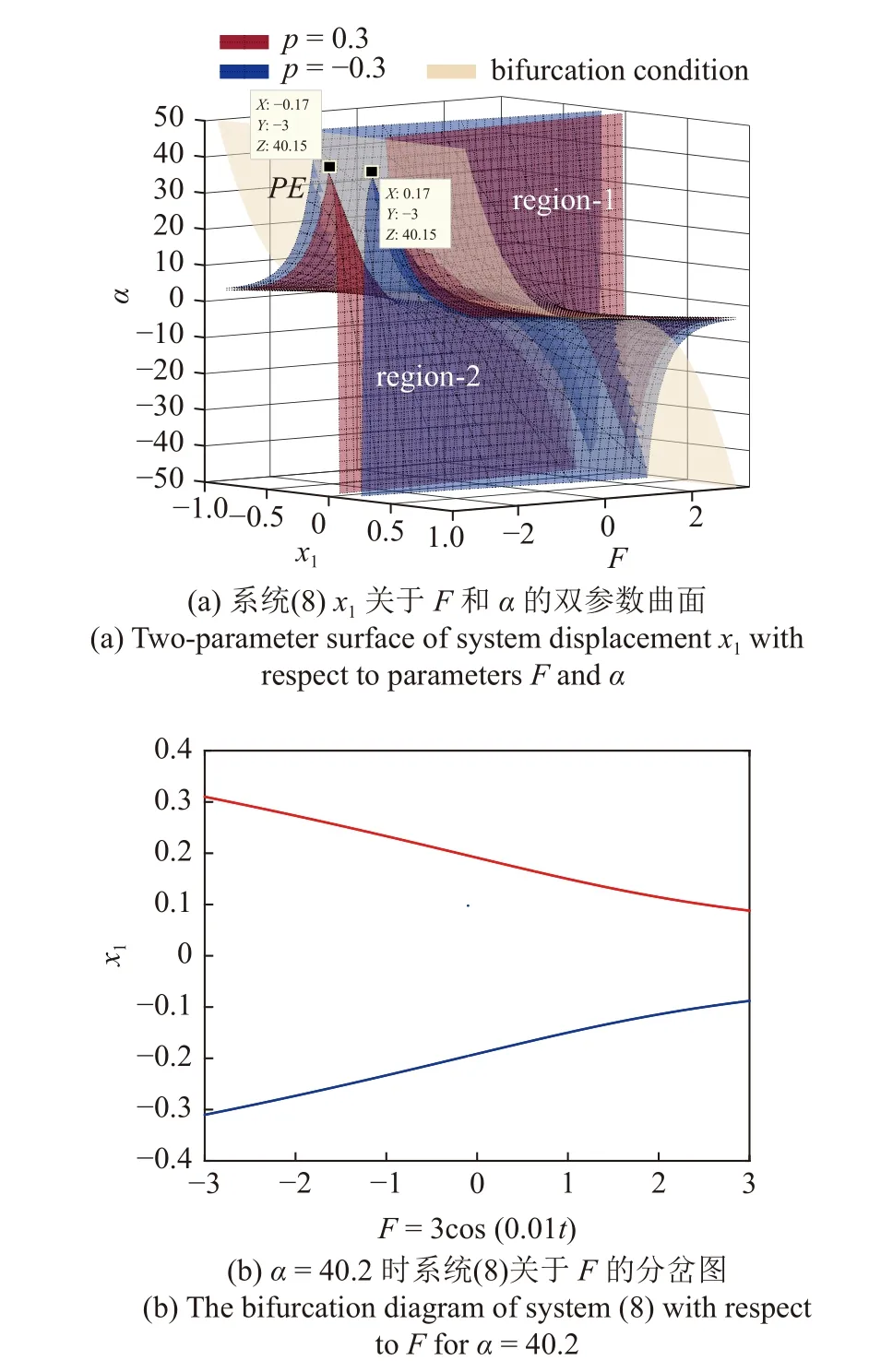
图14 自治系统双参数分岔曲面及在 α=40.2 时截面图Fig.14 Two-parameter bifurcation surfaces of autonomous systems and cross section at α=40.2

给出 α=40.2 时系统(5)和系统(6)的时间历程图对比,如图15 所示.可以看出,系统(5)呈现出明显的大幅振荡现象,在耦合Maxwell 元件后,系统呈现周期性簇发振动,大幅振荡得到明显抑制,振幅缩减50%以上.图16 是系统(6)转换相图与平衡线叠加,可以看到系统不再发生破缺分岔,轨线几乎完全包裹在P=±0.3 两条平衡线之间.

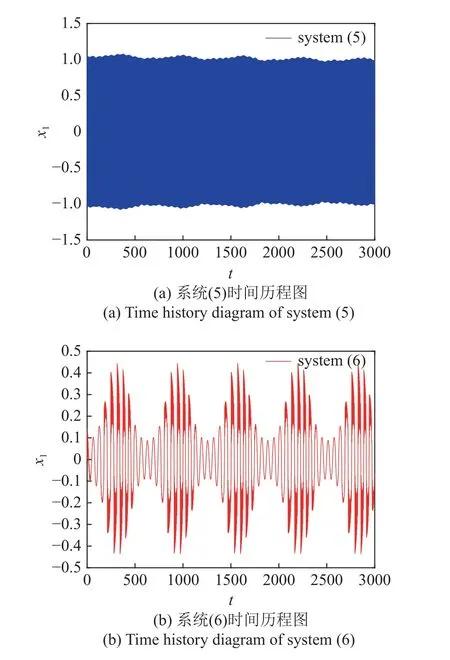
图15 α=40.2 时系统(5)与系统(6)时间历程图Fig.15 Time history diagram of system (5)and system (6)for α=40.2

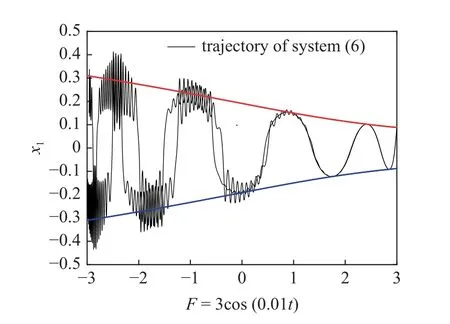
图16 α=40.2 时系统(6)转换相图与平衡线叠加Fig.16 The overlap of transformed phase portrait and bifurcation diagram of system (6)for α=40.2

如图17 所示,给出加入Maxwell 元件前后α=50时的时间历程图,此时系统不再发生破缺分岔,且在 α=50 时系统位移幅值降低约60%,优于α=1时的减振效果.

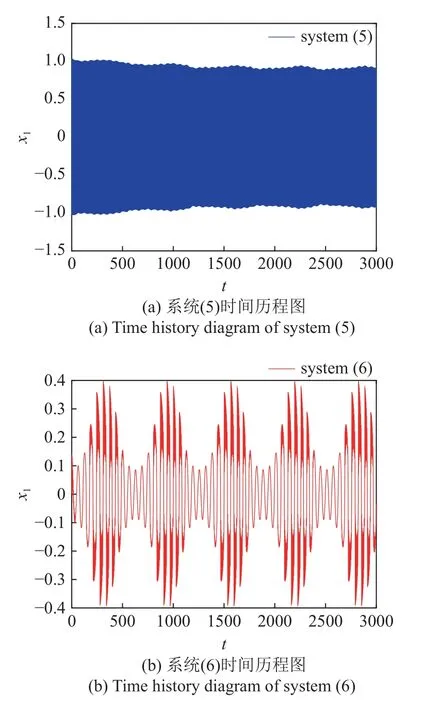
图17 α=50 时系统(5)与系统(6)时间历程图Fig.17 Time history diagram of system (5)and system (6)for α=40.2

5 结论

本文以具有周期性低频参数激励和外激励的Duffing 系统为例,探究耦合Maxwell 元件后,Zener 系统的振动控制问题.发现原系统的大幅高频振动在耦合Maxwell 元件后出现了激发态和沉寂态结合的簇发振动,并且位移和速度的振动幅值都明显降低.基于自治系统与非自治系统动力学行为的相关性,对耦合Maxwell 元件前后系统的稳定性和分岔进行了分析,发现系统发生破缺分岔.采用包络快慢分析法,将低频参数激励视作慢变量,结合外激励项被最值包络思想,详细给出了非自治系统受自治系统调节的机理.发现系统减振的主要原因有两个,其一是平衡点稳定性变化使得自治系统平衡线对非自治系统轨线的吸引性增强,导致轨线振动振幅降低;其二是非自治系统轨线总是在两条稳定的平衡线之间振动,也就是说,自治系统的平衡线限制了非自治系统的振动范围.另外,基于双参分岔分析,给出破缺分岔临界面,发现系统不发生破缺分岔的减振效果明显优于发生破缺分岔的减振效果.因此通过调节系统刚度系数和非线性项系数可以控制系统破缺分岔的发生,进而增强系统稳定性,提高系统的减振性能.