一种磁力滑动式翼型颤振能量俘获器1)

李支援 吕文博 马小青 周生喜

(西北工业大学航空学院,西安 710072)

引言

绿色能源技术被广泛应用,包括太阳能发电技术、风能发电技术、振动能量俘获技术等.振动能量俘获技术[1-3]主要关注低功率应用场景[4-6],已成为替代常规化学电池和减少布线的最有前途的选择之一.风致振动[7-10]是航空、轨道交通和其他相关领域常见现象.得益于振动能量俘获理论与技术的发展,风致振动能量可以被转化为电能.根据其中的振动原理,主要有4 种类型: 颤振式[11-12]、涡激式[13-15]、驰振式[16-17]和尾流驰振式风致振动能量俘获器[18-19].

颤振式能量俘获器具有大幅值响应特性,在高风速下具有良好的输出特性[20].为了有效俘获风致振动能量,学者们常基于压电效应设计压电式颤振能量俘获器.如Bibo 等[21-22]使用带有翼型的压电悬臂梁来俘获风能和周围环境的振动能量.Tian 等[23]研究了准定常气动模型、动态失速模型和非定常气动模型在颤振能量俘获器的性能预测方面差异,结果显示非稳态模型可以更准确地预测其输出响应.田海港等[2]提出了一种新颖的翼型颤振压电能量俘获器,可获得最大输出电压为17.88 V,功率为1.278 mW.

基于线性结构的风致振动能量俘获器存在一些缺点[24],如容易发散、高临界风速等.为了解决这些问题,研究人员通过引入非线性机制将收集器设计为非线性结构,并取得了显著的效果[25].Li 等[26-27]研究了磁耦合颤振能量俘获器和双稳态颤振能量俘获器,建立了它们的理论模型,并通过风洞实验进行了验证,结果显示磁耦合非线性能够降低颤振风速并改善输出性能.Zhou 等[28]设计了宽风速范围和高性能的动态多稳态颤振能量俘获器,可在低风速下呈现双稳态特性,在高风速下呈现三稳态特性.为了高效俘获风致振动能量,本文提出了一种磁力滑动式翼型颤振能量俘获器.基于半经验的非线性空气动力学模型和考虑磁铁位置的机电耦合系数,建立该能量俘获器的数学模型.搭建了风洞实验平台,以验证数学模型的正确性,并分析了该能量俘获器的输出性能.

1 结构与原理

本文设计的磁力滑动式翼型颤振能量俘获器主要结构如图1 所示.两个翼型上下对称布置,通过转轴和两个转动轴承实现与滑动连接件的铰接(下文中将两个翼型视为一个整体).两个悬浮磁铁左右对称布置安装在滑动连接件两端,滑动连接件内嵌前后两个滑动轴承.两个滑动轴承分别套在两个滑动导柱上,两个滑动导柱固定安装在两个对称布置的支座上.两个固定磁铁和导线线圈分别安装于两端支座上,并且同轴线布置.另外,翼型通过两个上下对称布置的弹簧与连接件连接,弹簧弹力为翼型的俯仰(扭转)运动提供回复力.磁铁排斥力为翼型的沉浮(滑动)运动提供回复力.该能量俘获器安装在风场环境中,气流经过翼型结构将产生升阻力和力矩,当风速达到系统的临界风速时,气动阻尼超过机械阻尼和电阻尼,系统将呈现等幅值振动,也即极限环振荡.滑动磁铁在线圈内的运动将会改变线圈内的磁通量,从而产生感应电压,通过接通外部负载为其供电实现风致振动能量俘获.将传统的压电式颤振能量俘获器改进为电磁式颤振能量俘获器,采用滑动的形式进行能量俘获,可以一定程度避免压电材料等的疲劳问题.并且该结构由于不是利用材料变形产生的能量,而是电磁感应,这可以充分利用结构大幅值振动进行能量俘获而不产生结构破坏,从而充分利用颤振的优势.

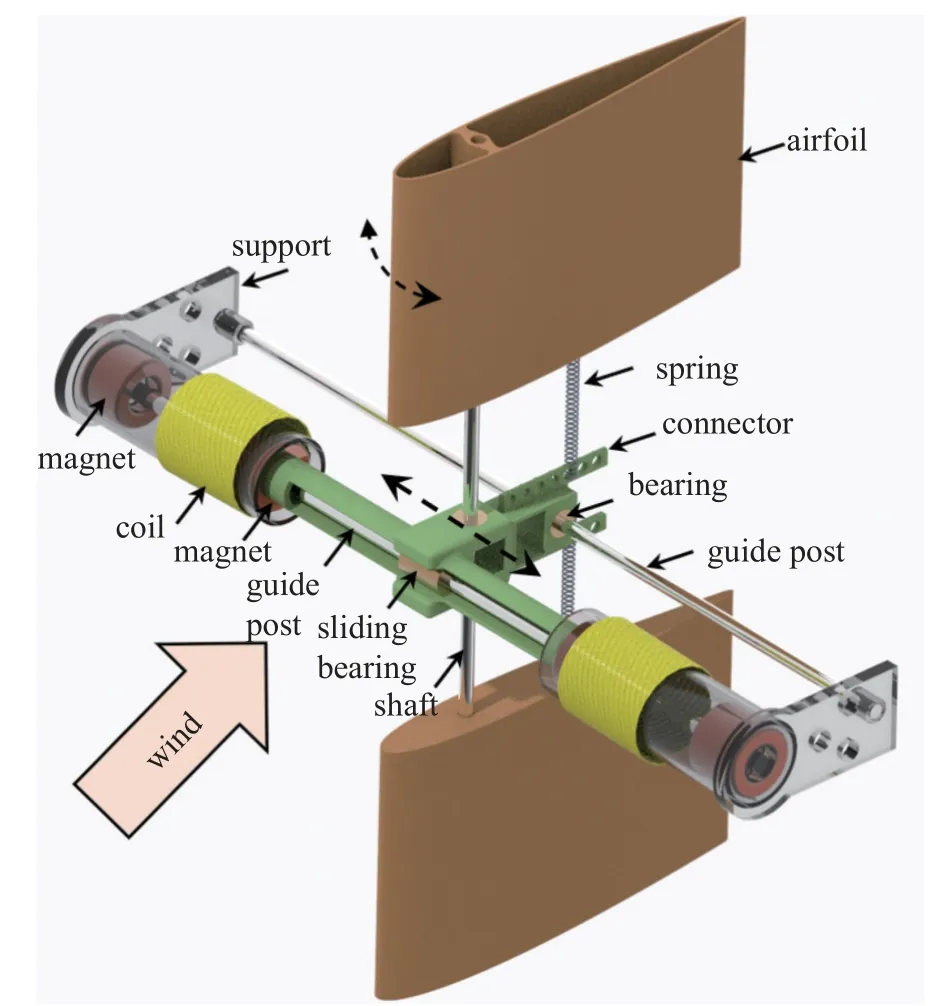
图1 磁力滑动式翼型颤振能量俘获器Fig.1 The magnetic sliding airfoil flutter energy harvester

2 动力学模型

该能量俘获器包括两对感应线圈和滑动磁铁,若磁铁平衡位置在线圈中间位置,则两个线圈产生的感应电压将不存在相位差可进行直接串联与并联.本研究采用并联方式,将能量俘获器视作电压源、内电阻Rc和电感Lc的组合,整体等效电路如图2 所示.

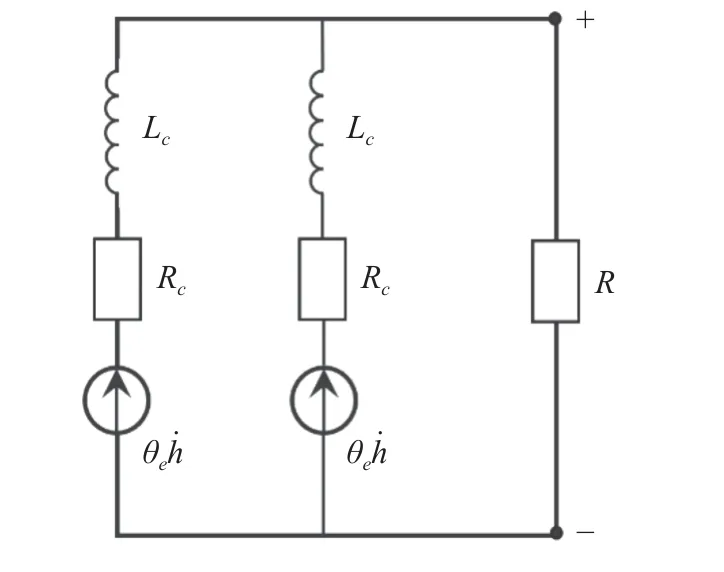
图2 等效电路Fig.2 Equivalent circuit

根据翼型颤振模型[11,29]和等效电路关系可得该能量俘获器的机电耦合动力学模型

其中,h为翼型的沉浮运动位移,α 为俯仰运动位移,I为流过负载电阻R的电流,M1为整体结构的等效质量(能量俘获器中能移动的所有结构质量和),mF为翼型质量,b为半弦长,xα为动态不平衡系数,Ch为沉浮运动阻尼系数,K1为沉浮运动线性刚度系数,K3和K5为沉浮运动非线性刚度系数,Iα为机翼转动惯量,Cα为俯仰运动阻尼系数,Kα1为俯仰运动线性刚度系数,Kα3和Kα5为俯仰运动非线性刚度系数,QL为气动升力,QM为气动力矩,θe为机电耦合系数.机电耦合系数根据磁通量的变换与位移之间的关系可以推导出具体表达式[30]

其中,Vm为磁铁体积,Br为剩磁密度,fc=NπD2w/(4Ac)为线圈填充密度,N为线圈圈数,Dw为线圈导线线径,Ri为线圈内径,Ro为线圈外径,hc为线圈高度,为振动过程中磁铁中心位置相对线圈底面的位置,Ac为线圈横截面面积.

当翼型振动过程中的攻角较大时将会产生动态失速的现象.为了充分考虑动态失速现象,本文采用了半经验的非线性空气动力学模型,该模型已通过实验验证[11,29].气动升力、力矩和阻力可以表示为

其中,s为翼型展长,CL,CD和CM分别是升力、阻力和力矩系数,可以通过求解以下微分方程获得

非线性偏差函数 ∆Cz表示非线性气动力与相应的线性静态气动力之间的偏差,表达式为

其中,Czs(θ)为静态气动力.CLs,CMs和CDs表达式为

r1,r2和r3由如下公式计算[11]

在大攻角下,r10,r12,r20,r22,r30和r32这些系数是不同振荡翼型的升力和力矩系数的实验数据.可以在参考文献[11]中找到上述相关系数的值.使用龙格库塔方法求解微分方程组式(1)～式(3)和式(9)～式(11)即可求出该能量俘获器的位移和电压时域响应.

3 风洞实验与数值仿真

3.1 风洞实验系统

本文搭建了风洞实验平台如图3 所示.该风洞能够通过变频器控制风洞试验段在0～30 m/s 风速范围内产生稳定风速.风洞试验段尺寸为400 m×400 mm×800 mm.实验中测量定风速下的位移响应和电压输出响应,实验环境中风速微弱,对风洞风速影响较小,风速波动很小.能量俘获器使用支撑件安装在风洞测试段内,两个线圈并联、与电阻箱相连,使用激光位移传感器测量翼型的沉浮运动位移(激光位移传感器测量机翼转轴的振动位移),使用示波器实时采集电阻箱两端电压和激光位移传感器数据.使用微差压计实时测量风洞试验段风速.翼型、底座和支撑件采用3D 打印制作.为了避免产生涡流,转轴和滑动导柱使用陶瓷轴.该能量俘获器参数如表1 所示.线圈参数:Ac,N,Dw,Ri,Ro,hc分别为5.3×10-5m3,1200,2.0×10-4m,0.013 m,0.015 7 m,0.02 m.该能量俘获器的沉浮运动刚度由两端磁铁排斥力提供.如图4 所示,使用测力计测得滑动磁铁与固定磁铁之间的排斥力f(x)和两者之间的距离x.用多项式形式拟合磁力f(x)与x之间的关系

表1 能量俘获器参数Table 1 Basic parameters of the harvester

图3 风洞实验平台Fig.3 Wind tunnel experimental platform

图4 回复力测试Fig.4 Measurement of the restoring force

图5 所示为振动过程中磁铁相对位置和受力关系,该能量俘获器处于初始静态稳定点时,滑动磁铁到固定磁铁的距离为x0,当振动时,沉浮位移为h.忽略磁铁A 对磁铁C 的磁力和磁铁D 对磁铁B 的磁力.滑动磁铁B 与滑动磁铁C 所受排斥力分别为f(x0+h)和f(x0-h),则两滑动磁铁排斥力的合力可表示为

提取h,h3和h5系数可得刚度系数(运动正方向与弹性回复力正方向相反)

通过上述过程获得的磁力与x之间的关系以及沉浮方向回复力曲线如图6 所示.角位移传感器转轴与翼型转轴固定连接,扭转过程中使用万用表测量角位移传感器的电压换算为角度α(对应关系为:0～10 V 对应0～2π,测量原理图如图7 所示).使用测力计推动翼型偏转,测力计测量扭转回复力fα(α),回复力扭矩为Mα(α)=fα(α)·x1,x1为测力计测点与转轴之间的距离.用多项式形式拟合扭转回复力矩与转角之间的关系曲线如图8 所示.根据上述实验拟合数据得到Kα1=0.004 685 N·m,Kα3=0.035 2 N·m,Kα5=-0.013 53 N·m.

图6 沉浮刚度实验数据与拟合Fig.6 Experimental data and fitting curve of plunging stiffness

图7 扭矩与转角测试示意图Fig.7 Torque and angle test diagram

图8 俯仰刚度实验数据与拟合Fig.8 Experimental data and fitting curve of the pitching stiffness

3.2 能量俘获性能

根据能量俘获器参数和第2 节提供的动力学模型,计算得到翼型的俯仰的均方根位移随风速变化曲线如图9(a)所示.数值仿真中,h的初始值分别取为0.02 m (图中红色曲线所示)和0.001 m,其余自由度的初始值均为0.图中可知,该能量俘获器的临界风速为5.5 m/s.风速6.8 m/s 到 8.2 m/s 之间为一段多解区域,出现了两个突跳点(初始值不同突跳点位置可能不同,想要讨论所有情况需要大量的计算,为了方便,本文仅以初始值0.02 m 和0.001 m 为例讨论),这是典型的强非线性响应现象.该能量俘获器中气动力是非线性的俯仰运动和沉浮运动的刚度也都是非线性的,因此,出现了多解区和突跳.一般来说,多解现象可能有利于能量俘获,如本结构中多解区中存在高能轨道和低能轨道,高能轨道能量俘获效果更好.

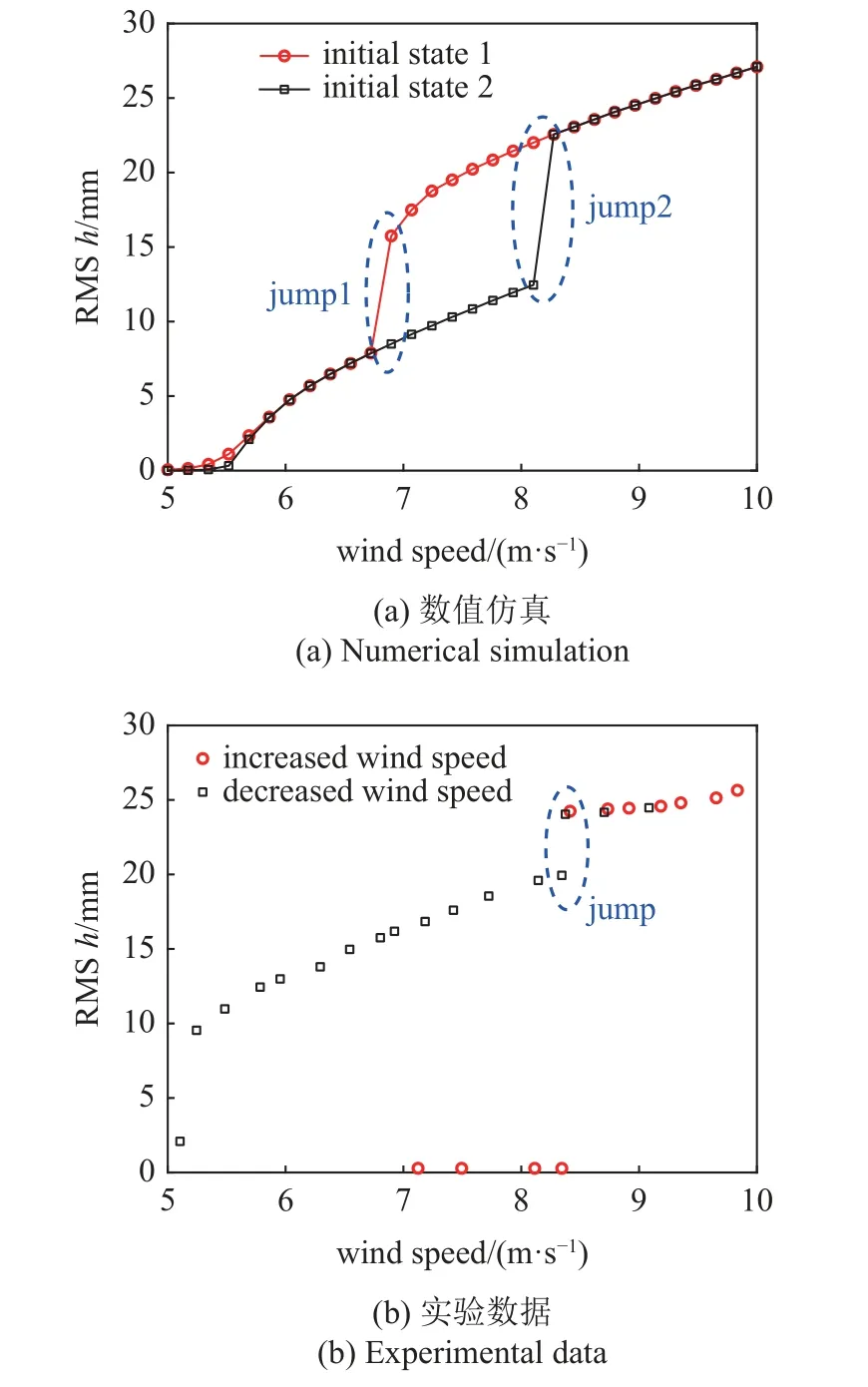
图9 不同风速下均方根沉浮位移Fig.9 Root mean square (RMS)plunging displacement at different wind speeds

图9(b)为实验中翼型的俯仰均方根位移随风速变化图,实验中采用了两种变风速手段,一种使用增加风速的形式获得特定风速(图中红色圆点),另一种为降低风速得到特定风速(图中黑色方点).升风速与降风速通过使用变频器改变风机的频率以改变转速的方式实现.升风速的过程为给定一个较低的频率启动风机,此时风洞风速较低(低于能量俘获器最低的临界风速),该能量俘获器处于静止状态,无振动响应.然后缓慢增加变频器频率以增加风洞的风速.当风速超过能量俘获器的临界风速时该能量俘获器将产生极限环振荡和稳定的电压输出.每增加一小段风速测量一次定风速状态下的振动位移和电压输出.降风速的过程是在能量俘获器静止状态下以一个较高的频率启动风机,该状态下风洞的风速较高已经超过能量俘获器的临界风速,使其产生极限环振荡和稳定的电压输出,然后降低风机频率以降低风速,每降低一小段风速测量一次定风速状态下的振动位移和电压输出.从而实现两种实验条件下的响应.实验中的每个数据都是在升降风速之后的定风速响应下的结果,两种初始状态的区别为:在升风速实验条件下,稳定风速之前能量俘获器以小振幅振荡或者为静止状态,在降风速实验条件下,稳定风速之前能量俘获器以大振幅振荡,以探索不同初始状态下的系统响应差异.下文中使用‘升风速’和‘降风速’指代该数据点的风速是通过升风速或降风速获得的.实验发现,该能量俘获器的临界风速有两个,一个是5.2 m/s,一个是 8.3 m/s.降风速时,在8.3 m/s 时也出现了突跳现象,但是仅找到一个突跳点.实验中升风速情况下在低于8.3 m/s 时能量俘获器没有振动响应,在达到8.3 m/s (8.3～8.4 m/s 之间,这里仅保留一位小数)时直接进入高能轨道.实验与仿真的差异主要是没有考虑滑动轴承的静摩擦和动摩擦的区别.我们发现在能量俘获器静止时,滑动轴承的摩擦阻力较大,而动态摩擦较小.因此实验中从静止状态激发为极限环响应较为困难,所以升风速的临界风速较高.而采用降风速手段,即直接给定一个高风速,使能量俘获器产生颤振,然后一点一点降风速的过程不存在静摩擦的情况,所以临界风速较低.另外实验中当风速低于8.3 m/s 时没有找到第2 个突跳点和多解区,这是因为风洞实验无法直接给定初始状态,仅能通过升降风速的手段提供两种不同的初始状态,所以风洞实验很难获得所有的响应状态.另外,当风速低于8.3 m/s 时(降风速实验)处于低能轨道响应位移的仿真值与实验结果具有较大误差.如当风速为8.1 m/s 时,均方根沉浮位移的仿真值为12.5 mm,实验结果为19.6 mm.影响实验结果与仿真结果之间差异因素有很多,较为明显的影响因素为系统存在气动阻尼且可能存在非线性阻尼,而仿真中采用的是线性阻尼.另外,仿真模型具有局限性,如式(14)～式(19)中存在较多经验参数也具有一定的误差.风洞与能量俘获器支架的振动同样会影响实验中能量俘获器的振动响应.由于准确测量系统响应的阻尼,以及避免风洞振动等干扰因素较为困难,因此本文主要关注该能量俘获器的响应趋势的仿真结果与实验结果是否吻合.

图10 为图9 对应的输出电压曲线,整体趋势与图9 保持一致.仿真中当风速达到10 m/s 时均方根电压达到了0.65 V,实验中当风速达到 9.8 m/s 时(升风速实验)均方根电压达到了0.57 V,8.3 m/s 左右突跳前的均方根电压为0.35 V 突跳后为0.46 V,增加了 31.4 %.图11 给出了风速为9.1 m/s (升风速实验)时的时域沉浮位移.仿真波形与实验波形基本一致,以一种近似正弦的形式响应,对应的频域曲线(通过快速傅里叶变换得到)如图12 所示.仿真的沉浮位移的响应频率为 6.3 Hz,实验中为5.1 Hz.误差主要来源于实验测定的回复力数据有误差和数据拟合误差,导致等效刚度不同.响应位移以一次谐波为主频率,存在较小幅值的3 次谐波,非线性不明显.

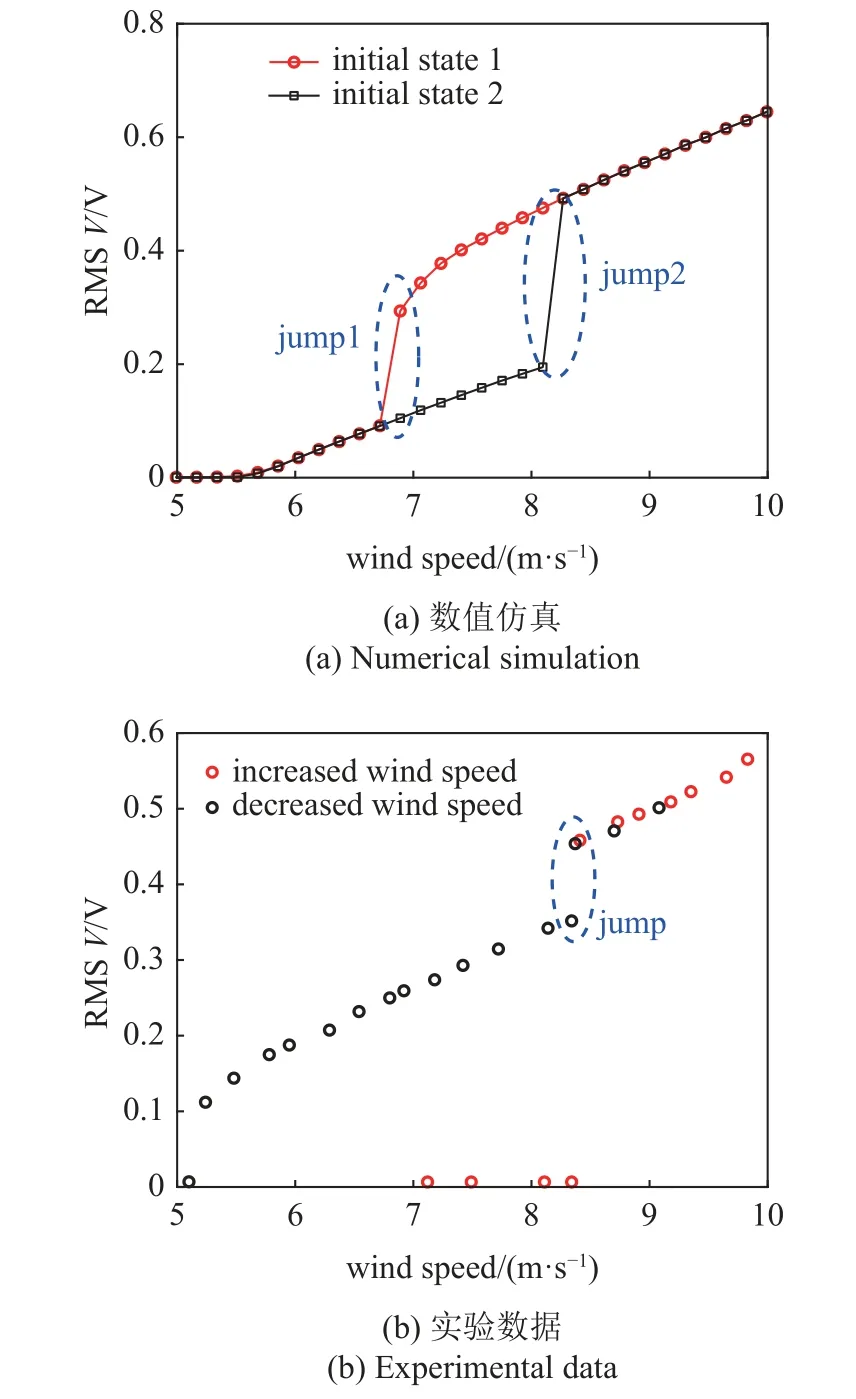
图10 不同风速下均方根电压Fig.10 RMS voltage at different wind speeds

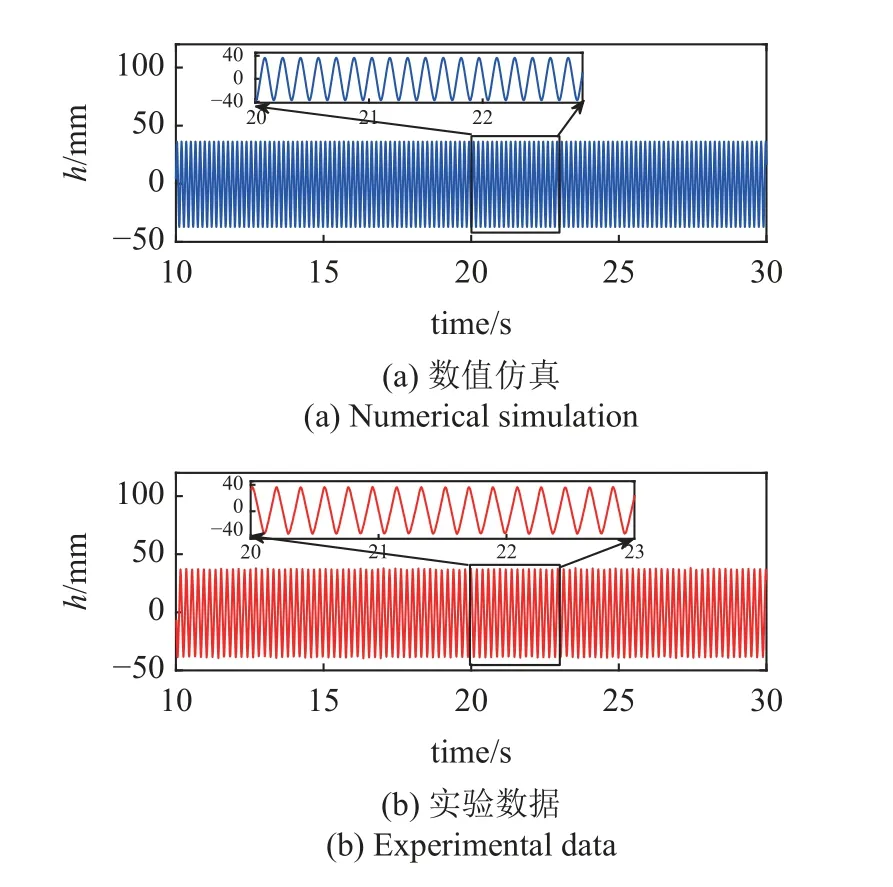
图11 风速为9.1 m/s 时的时域沉浮位移Fig.11 Time-domain plunging displacement at a wind speed of 9.1 m/s

图12 风速为9.1 m/s 时的频域沉浮位移Fig.12 Frequency-domain plunging displacement at a wind speed of 9.1 m/s

图13 为风速为9.1 m/s 时(升风速实验)的时域电压,可以看到,仿真波形与实验波形基本一致,并且以非正弦形式响应,这是因为机电耦合系数为非线性的(式(4)).对应的频域曲线如图14 所示,与响应位移不同的是,响应电压中含有明显的偶次谐波,与波形不关于0 电压对称现象一致,这是典型的强非线性响应.另外响应电压的一次谐波频率是响应位移的一次谐波频率的两倍,这是因为磁铁在往复运动中向左向右运动是对称的,即一个运动周期将产生两个电压周期.

图13 风速为9.1 m/s 时的时域电压Fig.13 Time-domain voltage at 9.1 m/s

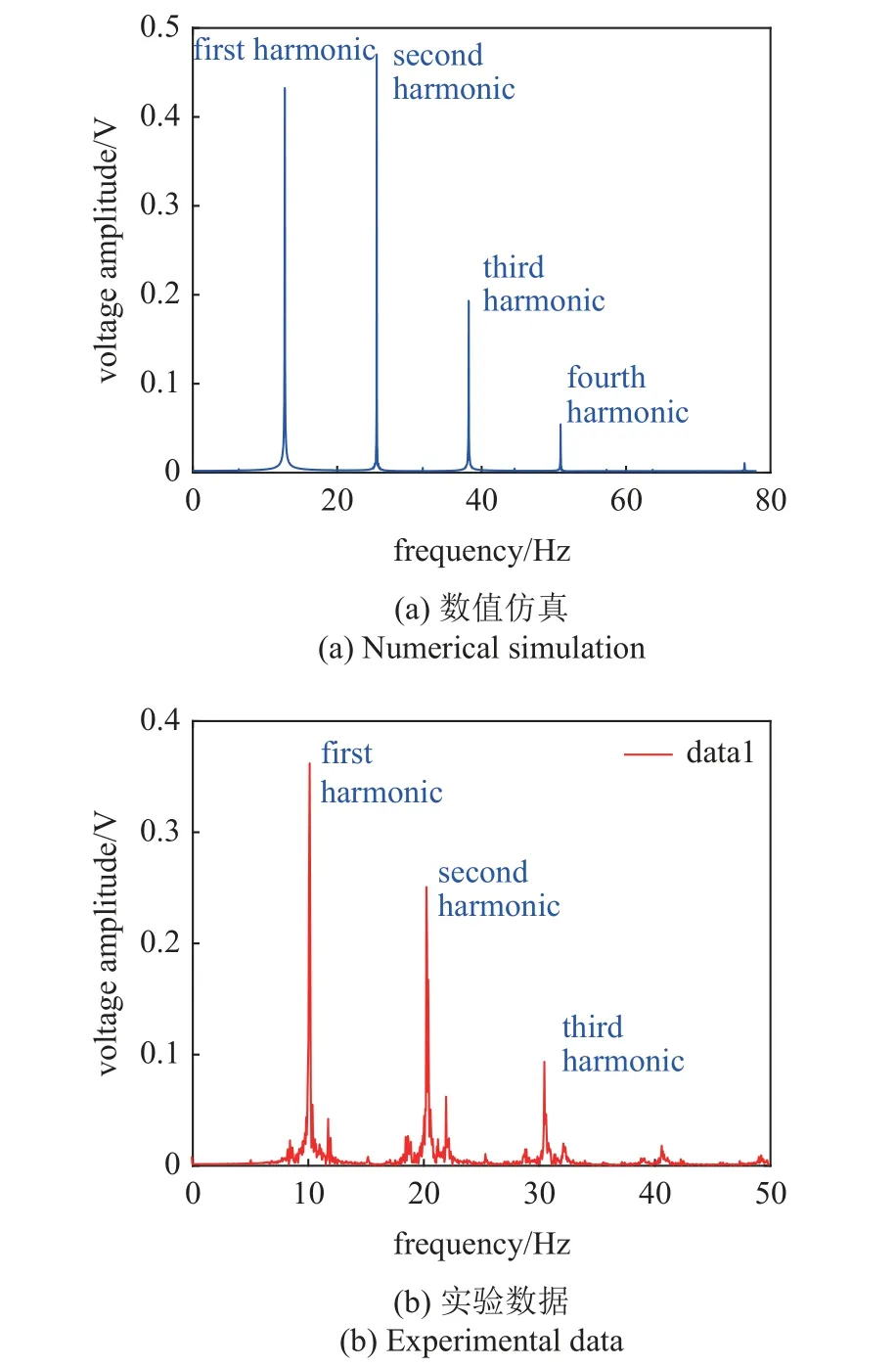
图14 风速为9.1 m/s 时的频域电压Fig.14 Frequency-domain voltage at 9.1 m/s

为了分析负载电阻对能量俘获性能的影响,本文绘制了均方根电压随负载电阻变化曲线如图15所示.可以发现,均方根电压随电阻的增加而增加,并且在电阻超过线圈内阻时增强趋势放缓.绘制平均功率随负载电阻变化曲线如图16 所示,可以看到,平均功率随电阻增加呈现先增加后降低的趋势,在线圈内阻附近达到最大值(数值仿真: 8.5 mW,实验结果: 7.5 mW).

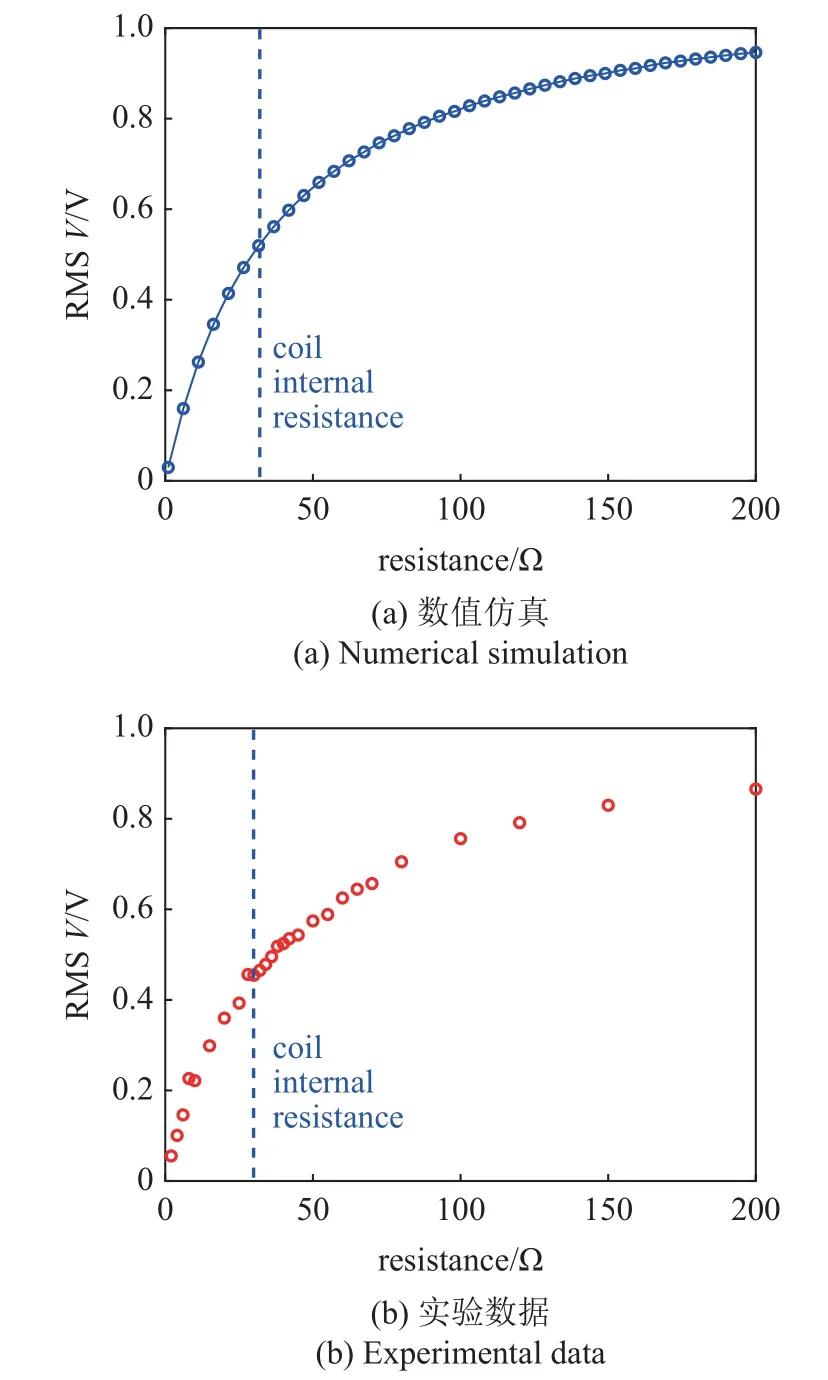
图15 风速为8.6 m/s 时的均方根电压随负载电阻的变化Fig.15 Variation of root mean square voltage with load resistance at a wind speed of 8.6 m/s

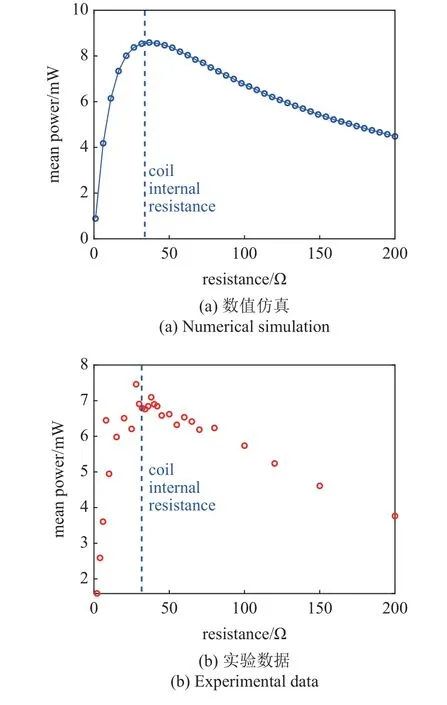
图16 风速为8.6 m/s 时的平均功率随负载电阻的变化Fig.16 Variation of average power with load resistance at a wind speed of 8.6 m/s

实验结果与仿真结果吻合较好,验证了理论模型的正确性.该能量俘获器能够在高于5.2 m/s 的风速下平均功率达到mW 级,并且风速越高输出功率越高.需要指出的是,该能量俘获器在静止状态滑动轴承与滑动导柱之间存在明显的静摩擦,导致升风速时的临界风速较高,不利于能量俘获,这是该结构的局限性.在风洞实验中如何在多解区域激发出高能轨道,并且寻找其他突跳点,以分析其输出性能是个难点,这部分内容将在后续研究中得到解决.另外,本文提出的磁力滑动式翼型颤振能量俘获器不受材料疲劳和大变形结构破坏的限制,因此该能量俘获器相对于压电式能量俘获器具有非常好的环境适应性.但该结构易受到电磁干扰的影响,因此该能量俘获器最好的工作场景为远离电磁干扰的空旷环境,如具有高于5.2 m/s 环境风的山区、高原和沙漠等,可为这些场景下的温湿度、光照等环境监测传感器供电.

仅使用数值方法研究强非线性现象具有一定的局限性,如该能量俘获器在6.8～8.2 m/s 之间存在多解现象,数值方法仅能求解出稳定解,并且求解所有稳定解需要大量的计算.对于这些强非线性现象的求解与分析,解析与半解析方法则是更有效的手段.但由于本结构可能存在大攻角响应,采用的半经验非线性空气动力学模型引入了较多的自由度,求解其解析解过于困难,因此对于该能量俘获器的求解可以采用半解析方法如增量谐波平衡方法[24,31].这部分工作将在后续研究中开展以深入分析该能量俘获器的非线性响应特性.

4 结论

本文提出了一种磁力滑动式翼型颤振能量俘获器,建立了其动力学模型,进行了风洞实验.通过升风速实验和降风速实验为能量俘获器提供两种不同的初始状态.实验结果表明该能量俘获器具有两个临界风速: 5.2 m/s 和 8.3 m/s.降风速实验中在8.3 m/s 时出现突跳现象,直接从静止状态进入高能轨道.数值仿真中在 6.8 m/s 和8.2 m/s 处出现了两个突跳点,和一段多解区域.实验中没有找到多解区域,如何在多解区激发高能轨道以及如何从静止状态激发极限环响应是实验难点.沉浮位移以正弦形式响应,输出电压以非正弦形式响应,并且出现明显的偶次谐波.均方根电压随电阻的增加而增加,平均功率随电阻增加呈现先增加后降低的趋势.在8.6 m/s 风速下,能量俘获器的负载电阻接近线圈内阻值时平均功率达到最大值7.5 mW.本研究可为设计高性能和高环境适应性风致振动能量俘获器提供重要参考.