一种二进制域非相邻表示型的生成算法

2023-11-15蒋洪波李钊枢林宪峰杨庆江冯新宇

黑龙江科技大学学报 2023年5期

蒋洪波, 李钊枢, 林宪峰, 杨庆江, 冯新宇

(1.黑龙江科技大学电子与信息工程学院, 哈尔滨 150022; 2.国网黑龙江省电力有限公司黑河供电公司, 黑龙江黑河 164300)

0 引言

椭圆曲线加密的核心运算就是标量乘。标量乘的窗口非相邻表示型NAF算法[1]分为两步:第一步需要先将标量k表示成NAF型记为F(k);第二步采用F(k)与椭圆曲线上的点进行标量乘计算。文献[2-3]中的标量乘算法均采用以上两个步骤,诸如此类标量乘算法中使用的NAF值计算都是窗口宽度w的NAF算法[1]。目前,对标量乘的研究较多,而对NAF算法的研究非常少。改进的NAF算法[4-5]在计算速度上进行了提升,但生成的NAF值所需存储空间较大。蒋洪波等[6]则在二进制NAF的存储空间上进行了优化,且占用空间有了较大幅度压缩,其仅对窗口宽度为2的NAF型进行了改进,而NAF算法的窗口宽度w可以满足w≥2,且为了达到提升标量乘的速度,选择宽度大于2的情况较多,因此,研究一个在存储空间上有优势的NAF算法还是非常有必要的。

1 非相邻表示型

非相邻表示型定义:若一个正整数k使用带符号的二进制(1、0和-1)来表示,其表达式为

(1)

其中,ki∈{-1,0,1},kl-1≠0,l为NAF的长度,且不存在两个连续的非零数字ki和ki+1。

1.1 非相邻表示型性质

窗口的宽度w≥2时,k的NAF表示成Fw(k),当w=2时,k的NAF表示成F2(k)。为了简洁通常也将其简写成F(k),关于F(k)的性质参见定理3.29[1]。定理3.33[1]给出了正整数k的Fw(k)性质:

(1)对于k有唯一的宽度w的NAF表示,记作Fw(k)。

(2)F2(k)=F(k)。

(3)Fw(k)的长度最多比k的二进制表示的长度大1。

(4)在所有长度为l的Fw(k)中,平均非零数字的密度近似为1/(w+1)。

该性质涵盖了w=2时的性质,即涵盖了定理3.29[1]。

1.2 非相邻表示型算法

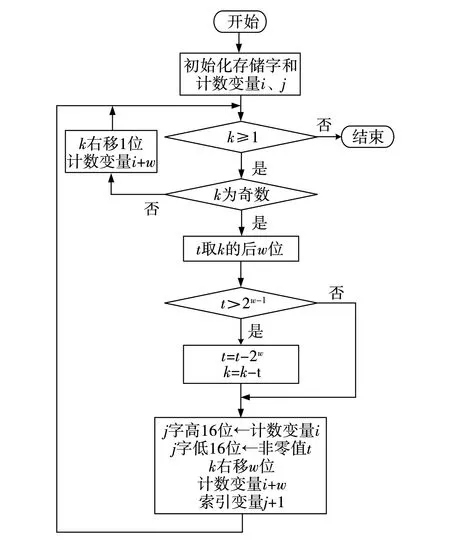
利用算法3.35[1]计算一个正整数k的窗口宽度w的Fw(k),从Fw(k)的最低位k0开始生成,如果k≥1,则重复执行,直至k=0为止。重复部分判断k。

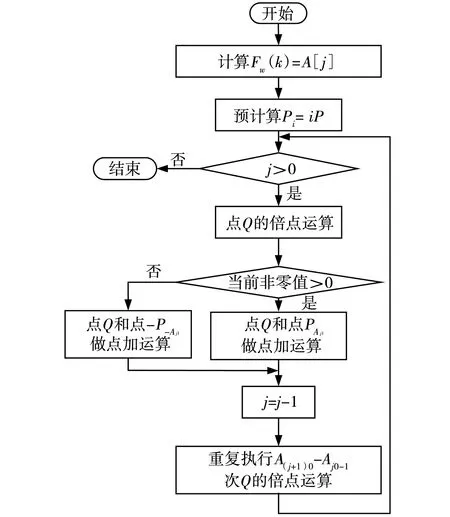
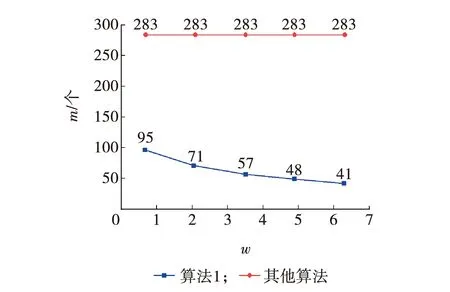
(1)若k为奇数,则用k对2w取余,余数值ki一定是奇数,且小于等于2w-1,又由算法3.35[1]可知,kmod 2w表示一个正整数u,u满足u≡k(mod 2w)且-2w-1

(2)若k为偶数,则ki=0。

(3)k=k/2,i=i+1。

基于此算法可以得到,k=1 122 334 455的NAF表示,如表1所示。

表1 正整数k=1 122 334 455的NAF对比

由表1可知,Fw(k)值都是由正负奇数组成的,且都在(-2w-1,2w-1)区间内。由表1可知,算法3.35[1]每次仅生成NAF的1位,即ki,生成步长为1,且每位ki单独存放在一个存储字中,如果这样以表1中的k值为例,则需要31个单元(或者字)存放该NAF值,而通过分析可知,NAF值中大部分为零值,根据性质(4)可知,非零值个数为其NAF值长度的1/(w+1),这是平均值,经分析会发现,其非零值的个数与w有关系,且最坏情况下其非零值的个数为l/w,也就是说非零值个数是小于等于l/w的。若l固定,则w越大非零值的个数就越少,存储那么多的零值就会显得浪费存储资源,所以只要将非零值存储起来并记录其在NAF值中的位置即可,这样在后边进行点乘计算时会方便许多。

2 字存储的NAF多位生成算法

2.1 NAF多位生成算法

在原来一次生成1位NAF值的基础上,分析可知,可以一次生成位或1位的NAF值,具体见文献[2]。在此基础上,将存储方式进一步改进得到算法1。该算法仅将非零值存储起来,对于表1中w=3时,不再需要31个单元存放数值,而仅需要9个单元即可,当w=6时,需要5个存储单元。

算法1基于字存储的NAF多位生成算法

输入:正整数k,窗口宽度。

输出:存放Fw(k)的数组A。

初始化:数组A[l/w];i=0;j=0;

k≥1时,重复执行;

若k为奇数,则t=kmod 2w;

若t>2w-1,则t=t-2w,k=k-t;

Aj0=i,Aj1=t;

k=k/2w;

i=i+w;

j=j+1;

否则,k=k/2,i=i+1;

返回数组A与j。

算法1中数组A的单元数量按照非零值数量的最坏情况(l/w)来预留单元。其Aj0和Aj1分别表示字的高16位和低16位(以字长32位为例),也就是说,使用字的高16位记录NAF值中非零值在原NAF中的位置,低16位存放具体的非零值。存储示意如图1a所示。当然算法1中还可以进一步优化,用一个字来存放两个NAF的非零值,也就是将32位按8位一划分,分成四个部分,分别存放两个相邻的非零值,存储示意如图1 b所示。这完全可以根据算法的应用环境来决定,当然使用16位存放非零值和使用8位存放非零值所表示的数值范围有着巨大的变化,使用8位可以表示的最大值为255,也就是说它可以用来存放w=9的NAF值。如果值再大就需要扩大存放位宽,就使用16位存放非零值可以存放最大w=17的NAF值,其实真正应用时用不到这么大的w。

图1 字存储示意

图1 b中的is和iv分别表示两个相邻非零值在NAF序列中的位置,ts和tv分别表示对应这两个位置的非零值。若对应表1中的w=3,则算法1计算完成后的存储内容,如图2所示。

图2 表1中w=3的数组存储示意

若采用8位存储的形式,则存储字个数会在算法1的基础上再折半,图2中使用了9个单元(字),那么采用8位存储就会使用5个单元(字)存放NAF的非零值。这里示意图不再给出。

算法中用来记录非零值在NAF中的位置,j表示第j个非零值(非零值的个数从0开始计数),当然最后它也表示数组A的最后一个非零值的索引位置,它将在做点乘时还要起到关键作用。经过以上分析,算法流程,如图3所示。

图3 字存储的NAF多位生成算法流程

该算法当k≥1不成立时结束,否则重复进行如下操作。判断k的奇偶性,结果有两种情况。

(1)当k为奇数时,取k的后w位,这里可以用t=kmod 2w实现,也可以用t=k&(2w-1)实现。然后判断t>2w-1是否成立,如果成立取t=t-2w,以保证t的值落入(-2w-1,2w-1)内,更新k的值取k=k-t。若不成立,则不用对取得的t值进行处理,也不用更新k的值,注意正常这里是需要对k做减t处理的,但是由于t(0,2w-1),k减t的结果就是k的后w位为0,后边还要一次性的整除2w,相当于对k右移w位,这样看来减与不减的意义不大,而且还浪费时间。至此已经得到了非零值和它在NAF中的位置,将两个值分别存入存储字的低16位和高16位。k的低w位处理完毕,需要更新k的值,做k整除2w或者k右移w位。记录非零值在NAF中位置的计数变量加w,表示一次处理了k的w位,而不是算法3.35[1]的一次处理1位,数组索引变量加1。

(2)当k为偶数时,即最低位为0,那么k的最低位转换成NAF时一定是1位零值,零值不需要存储,所以索引变量不进行处理,直接将k做除2运算,或者将k右移1位得到新的k值。虽然不记录该零值,但它却是NAF中的一位,因此,该算法中记录非零值在NAF中位置的计数变量需要加1。

2.2 基于字存储的NAF点乘算法

椭圆曲线中的标量乘也称为点乘。该算法使用NAF值时,可以用算法3.36[1]或算法1[7],然而当使用了算法1生成的NAF后,再用此算法就不合适了,因此此处给出相应的点乘算法2。

算法2基于字存储的NAF点乘算法

输入:正整数k,窗口宽度w,PE(Fq)。

输出:kP。

初始化:Q←∞。

用算法1计算Fw(k)=A[j];

对于i∈{1,3,5,…,2w-1-1}计算Pi=iP;

从j到0,重复执行;

Q←2Q;

若Aj1>0,则Q←Q+PAj1;

否则Q←Q-P-Aj1;

j=j-1;

从A(j+1)0-1到Aj0+1,重复执行Q←2Q;

返回Q。

算法2中根据非零值Aj1的正负决定加PAj1还是减P-Aj1,而减P-Aj1可以理解为加-P-Aj1。算法中使用了预计算,提前计算Pi=iP,由椭圆曲线的封闭性可知,该计算结果仍是椭圆曲线上的点。算法流程如图4所示。

图4 点乘运算流程

点乘计算开始时需要对Q点进行初始化,即Q点为∞,它表示在二进制椭圆曲线中唯一的一个无穷远点,用投影坐标可表示为(0∶1∶0),雅克比投影坐标表示为(1∶1∶0),点Q用来存放每次倍点或点加的结果,最后返回点乘的结果。图中点-P-Aj1可以理解为点P-Aj1的负点,若点P-Aj1的坐标为(X∶Y∶Z),那么-P-Aj1的坐标无论是投影坐标还是雅克比投影坐标都可表示为(X∶-Y∶Z)。

该算法用到的点加和倍点运算可以使用两种坐标表示的任何一种算法进行,具体算法可参见文献[1]。

3 算法分析及验证

算法从空间、时间和访问内存三方面进行分析。首先,空间上算法1计算的结果需要一个长度为j+1的一维数组存放,其中,j+1为实际NAF中非零值的个数,这里前提为数组从0开始索引,j在算法中的初始值为0,所以非零值的个数为j+1。因此,算法1需要的存储空间就是j+1个存储字。

而算法3.35[1]、文献[2]和[3]的NAF算法存储NAF值都需要L或L+1个字(L为k的二进制表示长度),又由定理3.33[1]的(3)可知,L和l满足L≤l≤L+1。根据(4)可知非零值的平均密度为1/(w+1)。

综合以上对比,可得到j+1≤(L+1)/(w+1),由此可以看出,存储空间得到了极大的节约。w值越大,节省空间越多。以NIST推荐的二进制域上的随机椭圆曲线m=283为例,即数据长度为283位,以上三种算法和算法1存储NAF值所占空间曲线如图5所示。图中,当数据k的二进制长度m=283且w=2时,算法1执行后会有平均95个非零值,即需要95个单元存放非零值及其在NAF中的位置,而算法3.35[1],文献[2]和[3]的NAF算法存储NAF值会需要283个,以此类推w=6时算法1执行完平均需要41个单元,其他三种算法还是需要283个单元,由此可见,算法1所需存储空间较其他NAF算法要少很多,且随着窗口宽度w的变大,算法1所需的存储空间越小。

图5 算法1与其他算法占用空间比较

特别说明,若w=2时,则就是求k的F(k),这里不建议用算法1,更建议用文献[4]的算法1,它能将存储空间进一步压缩。当3≤w≤17可采用文中的算法1求得NAF值,若w>17则可用单字的前n位存放非零值在NAF中的位置,单字的后32-n位存放非零值,具体要根据w的值来确定n的值,文中仅提供思路不再给出详细的算法。

其次,运算时间上算法1与文献[3]中的算法2基本相同。使用Linux平台gcc编译c对算法1和文献[3]的NAF算法建模,测试数据长度m选取NIST推荐的二进制域上的三个长度,具体测试数值参见表2。

表2 测试数据

由于每组数据每次测试时运行时间总是有些微不同,因此取每组数据测试后的平均仿真时间作为当前长度NAF算法的运行时间,算法运行时间比较,如表3所示。从表3可知,运行时间相差不大。

表3 两个NAF算法的运行时间

最后,从访问内存方面看,算法1存储非零值时需要访问内存j+1次,其他NAF算法则无论值是否为零都需要访问内存,即需要L或L+1次访问内存。算法2也仅需j+1次读取非零值,而文献[1]的点乘算法3.36需要访问L或L+1次内存以取得NAF的各位值,进而判断是否做点加运算。当然两个算法都需要j+1次读取预计算的Pi=iP值。因此,从这里可以看到,算法1和2在时间上还是要稍快于其他NAF算法和点乘算法的。