深厚换填砂土地基强夯有效加固深度的影响因素

2023-11-15赵延林龚雨林张子煜

黑龙江科技大学学报 2023年5期

赵延林, 龚雨林, 张子煜

(黑龙江科技大学建筑工程学院, 哈尔滨 150022)

0 引言

强夯法因其经济性与便利性,目前已经成为我国主要地基处理方法。强夯法加固设计标准之一就是土体经过强夯后,其有效加固深度应满足上部建(构)筑物在荷载作用下的变形要求。然而强夯有效加固深度的影响因素众多、复杂,且难以量化,因此研究强夯法有效加固深度的影响因素及其对有效加固深度的影响规律,对于强夯法设计与施工具有一定的指导意义。

近年来,国内外学者针对强夯有效加固深度开展了一定的研究工作。Gu等[1]通过试验数据研究了特殊点的土体变形规律,初步探讨了强夯有效加固深度的影响因素及其影响规律。田水等[2]利用显式动力学方法,分析了锤-土冲击碰撞过程中几个主要强夯工艺参数与土性参数对有效加固深度的影响情况。高政国等[3]分析了施工参数对有效加固深度的影响,并对强夯加固土体的塑性区增长规律进行了研究。费香泽等[4]利用读数显微镜位移跟踪法,通过改变夯击能、夯锤半径与土体密度等参数来研究影响夯实效果的因素。Pan等[5]对强夯的加固深度、夯击沉降量与表面最大加速度的关系进行了研究。林维泉等[6]通过实际工程中不同施工方案的对比,应用模糊优选理论分析了加固山区碎石地基有效加固深度的影响因素。赵婉[7]结合实际工程,建立了强夯法的数值分析模型,将数值模拟结果和试验结果进行对比分析,验证了数值模拟方法用于强夯计算的可行性。吴帅峰等[8]通过土石料强夯现场试验结果,提出了强夯法加固效果随夯击次数的增加而动态变化的规律。

就目前的研究而言,由于受到现场试验条件的限制,已有的研究主要表现为仅仅分析部分施工参数或土体参数对强夯有效加固深度的影响,缺乏对强夯有效加固深度影响因素的全面、系统性研究。因此,笔者以沈阳市某深厚换填砂土地基项目为工程背景,通过现场试验田试验与数值模拟相结合的方法,分析强夯施工参数(包括夯击能、夯击次数、夯击能组合、夯锤尺寸等)与土体物理力学参数(包括内摩擦角、泊松比、密度、弹性模量等)对深厚换填砂土地基强夯有效加固深度的影响规律,为实际工程的设计与施工提供理论依据与参考。

1 现场试验

本文依托沈阳市某工厂地基处理项目,现场试验田尺寸为45 m×45 m×10 m,采用挖掘机开挖,挖除表面耕土、粉质黏土及细砂,直至坑底的中砂层。然后进行砂土分层换填,中心区域为换填中粗砂,一般区域为换填混砂,换填厚度为8.35 m,并进行地基强夯处理。

强夯采用三遍强夯工艺,第一遍和第二遍采用3 000 kN·m夯击能平锤强夯,锤径2.5 m,锤重180 kN,落距16.67 m,每遍夯击时各个夯点的夯击次数为8～14次,收锤标准按最后两击平均夯沉量不大于5 cm,施工完成后及时将夯坑填平。第三遍用1 000 kN·m能级满夯,锤径2.5 m,锤重180 kN,落距5.6 m,每夯两击,要求夯印1/4搭接,以夯实地基浅层填土,满夯结束后整平场地。

强夯前,在试验田中心区取换填中粗砂土样进行室内土工试验,测得其主要物理力学参数,如表1所示。

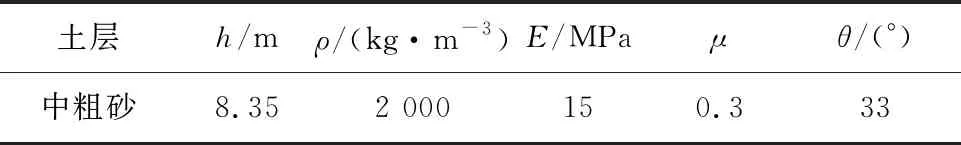
表1 换填土物理力学参数

分别对试验田中心区夯击点进行强夯前与强夯后的重型动力触探(DPT)试验,根据动力触探击数结果绘制出触探深度与动探击数之间的关系曲线,如图1所示。其中,N0为每10 cm的动探击数。

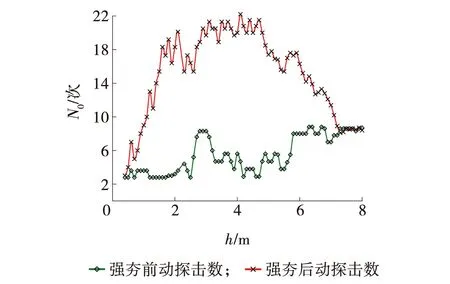
图1 重型动力触探(DPT)试验数据曲线

从图1中可以看出,强夯前不同深度处换填中粗砂的动探击数均在8次及以下,表明未经强夯处理的中粗砂密实度较差。而对于强夯后的中粗砂,从图1中还可以看出,地表以下0.5～2.0 m范围内的土体,其动探击数随埋深接近线性增长趋势,且增加幅度很大,由3次快速增加到20次,表明地表下2.0 m范围内中粗砂的加固效果受强夯振动的影响较大。地表以下2.0～4.7 m范围内的土体,其动探击数随埋深呈现出微小的波动,波动范围基本在20～21次,表明地表下2.0～4.7 m范围内中粗砂的加固效果最好,且受强夯振动的影响极小。地表以下4.7～7.2 m范围内的土体,其动探击数随埋深基本呈现线性减小趋势,且减小幅度较大,由21次快速减小到8次。在深度7.2 m处动探击数趋于稳定,与强夯前动探击数吻合,由此可判断该试验点的有效加固深度大约为7.2 m。

此外,通过测量强夯前与强夯后夯击点的高程,可以计算得到夯击点的累计夯沉量为1.32 m。

2 数值模型的建立

2.1 模型基本假设

应用ABAQUS有限元软件,建立上述工程试验田试验的强夯加固数值分析模型,采用的基本假设条件如下。

(1)模型中的夯锤与土体均假设为均质、各向同性材料。

(2)忽略强夯过程中夯锤与土体接触后发生的侧向滑移以及不同方向上的转动。

(3)根据地质勘查报告,地下水埋深较深,因此不考虑地下水渗透性影响。

2.2 模型尺寸与网格划分

依据现场试验田试验参数与文献[9],可计算得到强夯振动波横波波速vp=86.6 m/s、纵波波速vs=65.47 m/s。文献[10]研究表明,强夯对土体产生的振动波类似于地震波,振动频率在8～12 Hz之间。由此可得出强夯振动的波长为8.66～10 m。为考虑振动波在土体中能够充分传播,减小边界条件对模型计算精度的影响,故选取数值分析模型的三维尺寸为20 m×20 m×15 m。

强夯过程中土体会产生大变形,文献[11]研究表明,在进行土体动力分析时,网格尺寸应根据最高频率所在波长进行计算,即

(1)

式中:Δl——网格尺寸;

λ——最高频率对应的波长。

依据式(1),为提高计算结果的准确性和时效性,文中将夯锤以下土体网格尺寸设定为0.3 m,而模型边界处的网格尺寸设定为1.5 m,模型尺寸与网格划分,如图2所示。

图2 强夯模型网格划分

2.3 模型单元与计算参数

ABAQUS有限元软件中所有的单元都可以用于动力分析,在强夯巨大的冲击荷载作用下,使用一阶单元C3D8R网格单元(八节点六面体线性缩减积分单元)具有很好的一致性,能够更好地模拟应力波在土体中的传播,从而准确地体现出土体在强夯冲击荷载下的动力特性,土体的计算参数见表1。

夯锤选用圆柱体铁块,假定夯锤的刚度比地基土的刚度高很多,可视为刚性体,故给予其足够大的弹性模量,夯锤的计算参数见表2。

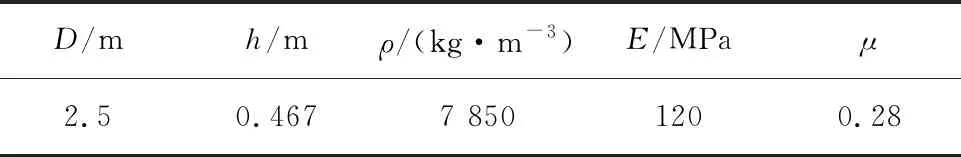
表2 夯锤计算参数

2.4 边界条件

边界条件对于模型计算结果影响较大,特别是在动力分析中,不合理的边界条件会导致计算收敛困难。在强夯过程中,夯击会产生巨大的振动波,为了减小振动波在土体边界发生反射,进而对计算结果产生影响。计算模型采用侧边界无水平方向位移,底部固定无水平和竖向位移,顶部为自由面。

2.5 本构模型

修正的Mohr-Coulomb模型是经典Mohr-Coulomb模型的延伸,它更加符合土体在外力作用下的变形特征,且可与线弹性模型联合使用。因此,在岩土工程中被广泛应用[9]。考虑现场实际工程情况,文中采用修正Mohr-Coulomb模型对强夯加固土体模型进行模拟计算。

夯锤的变形量相较于土体可忽略不计,视其为刚体,本构模型采用常见材料的线弹性模型。

2.6 土体弹性模量修正

在强夯加固施工过程中,每次夯击后夯击点附近土体均会产生较大的塑性变形,从而导致土性参数发生变化,在数值模拟中必须充分考虑这种土体参数变化对计算结果的影响。

文献[12]提出通过土体改性法来考虑夯击次数对土体参数的影响,即通过改变每次夯击后土体的弹性模量来等效土体参数的变化,并通过室内强夯模型试验获得了强夯过程中土体弹性模量的修正计算公式为

En=E×N0.516,

(2)

式中:En——夯击N次后土体的弹性模量;

E——土体初始弹性模量。

文中在数值分析过程中,将采用文献[12]所提出的土体改性法来考虑夯击次数对土体参数的影响。

2.7 冲击荷载模拟

针对强夯冲击荷载,文献[13]利用动态应变仪,记录夯击过程中动应力随时间的波形变化,得出夯锤对地面冲击碰撞过程中产生的应力波类似于三角形单峰荷载,且没有明显的第二应力波这一结论。故文中将强夯冲击荷载简化为三角形单峰荷载,并考虑夯锤自重。

由夯锤底面应力与夯沉量之间的关系可知:

πr2p=SU

(3)

式中:r——夯锤半径;

p——夯锤底面应力;

U——夯沉量;

S——土体的弹性常数。

(4)

式中:E——土体弹性模量;

μ——土体泊松比。

在强夯过程中,夯锤撞击土体时的运动方程可表示为

(5)

式中,m——夯锤质量。

将式(2)代入式(5),可得:

(6)

由式(6)可求得,夯锤冲击荷载的时程方程为

(7)

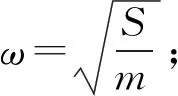
v——夯锤落地时的瞬时速度,可由自由落体运动求得。

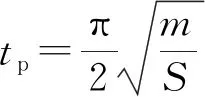
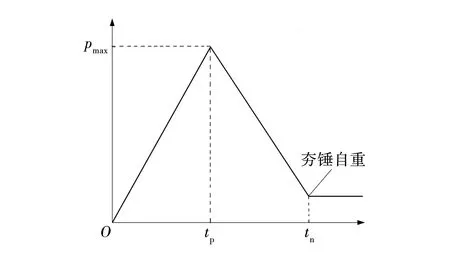
图3 简化的冲击荷载-时间曲线

2.8 模型合理性验证

按照上述方法建立换填砂土地基强夯法施工的数值分析模型,根据试验田试验的实际施工参数,夯锤重量为180 kN,锤径为2.5 m,落距为16.7 m,夯击能为3 000 kN·m,对土体进行14次夯击。

通过数值模型计算可得到地表夯沉量随夯击次数的变化曲线,如图4所示。其中,s为地表夯沉量。由图4可知,地表夯沉量随夯击次数的增加呈现非线性增加趋势,经过14次夯击后地表夯沉量为1.26 m,而现场试验田试验中测得的地表夯沉量为1.32 m,二者相差4.55%。

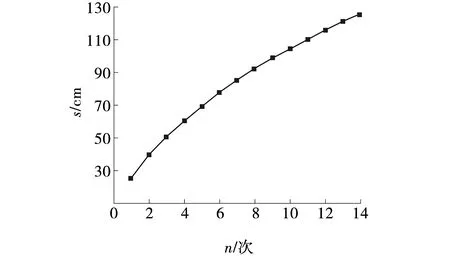
图4 不同夯击次数对应夯沉量

文献[14]通过粒径较大的粗颗粒土的强夯模型试验,提出以竖向位移为地表夯沉量5%的土体深度作为判定有效加固深度的依据。文中地表夯沉量的计算值为1.26 m,其5%为0.063 m,在土体竖向加固区找到竖向位移为0.063 m的点,它们形成一个包络面,则地表至此包络面的最大竖向距离即为有效加固深度。经测量得出该模型在3 000 kN·m夯击能作用下的有效加固深度为7.02 m,而现场重型动力触探试验测得的有效加固深度为7.2 m,二者相差2.5%。

由以上分析可知,经数值计算得到的夯沉量和有效加固深度分别与实测值相差4.55%和2.5%,表明按上述方法建立的数值分析模型可以较好地模拟换填砂土地基的强夯法施工过程。

3 有效加固深度影响因素分析

3.1 强夯施工参数

3.1.1 夯击能

夯击能是夯锤重量与落距的乘积,其中,夯锤重量和落距都是可变量。为减小夯锤下落过程中产生能量损耗误差,这里假定落距不变,通过改变夯锤重量的方式来表示不同的夯击能,进而分析不同夯击能对有效加固深度的影响。不同夯击能工况设置参数,如表3所示。

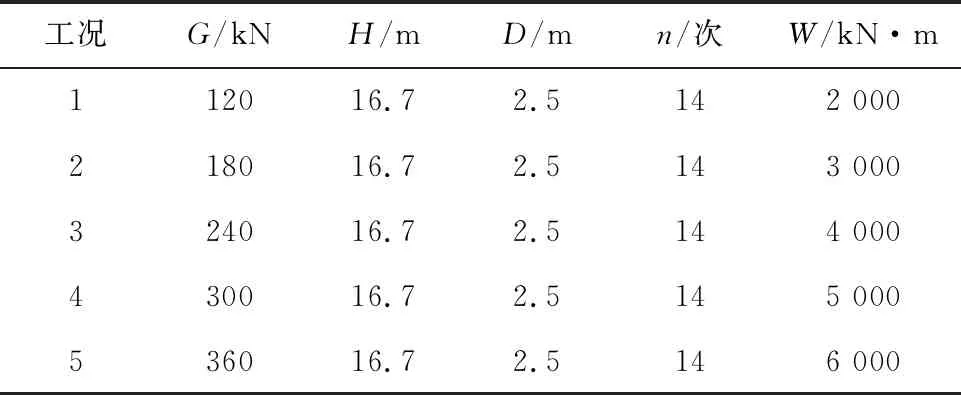
表3 不同夯击能工况参数

通过数值计算得到强夯有效加固深度d随夯击能的变化曲线,如图5所示。由图5可知,强夯有效加固深度随着夯击能的增加而增加,且受夯击能影响较大。当夯击能由2 000 kN·m增至3 000 kN·m,有效加固深度增加0.67 m。夯击能由3 000 kN·m增至4 000 kN·m,有效加固深度增加1.04 m。夯击能由4 000 kN·m增至5 000 kN·m,有效加固深度增加0.67 m。夯击能由5 000 kN·m增至6 000 kN·m,有效加固深度增加0.38 m。由此可见,随着夯击能的增加,有效加固深度增量呈现出先增大后减小的变化趋势,当夯击能取3 000～4 000 kN·m时,深厚换填砂土地基强夯加固效果最优。

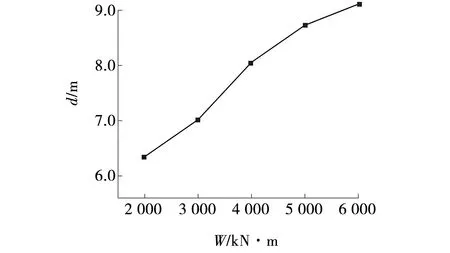
图5 不同夯击能下有效加固深度

3.1.2 夯击次数

保持锤重180 kN、落距16.67 m、锤径2.5 m不变,仅改变夯击次数,由数值计算得到强夯有效加固深度随夯击次数的变化曲线,如图6所示。从图6中可以看出,有效加固深度随着夯击次数的增加而增加,但增加幅度在逐渐减小。当夯击次数n≤3时,有效加固深度随夯击次数呈线性大幅增长,单击增幅为1.17 m。当3≤n≤9时,有效加固深度增量开始减缓,单击增幅由0.85 m缩减到0.26 m。当n>9时,有效加固深度趋于稳定,单击增量均小于0.13 m。由此可知,对于深厚换填砂土地基,强夯施工最优夯击次数为9次,当夯击次数超过9次时,其对强夯加固效果基本没有影响。

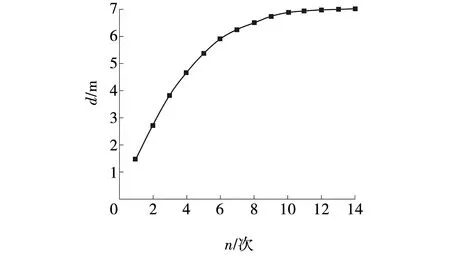
图6 不同夯击次数下有效加固深度

3.1.3 夯锤尺寸

保持锤重180 kN、落距16.67 m、夯击次数14次不变,仅改变锤径(分别为1.6、2.0、2.4、2.8、3.2 m),通过数值计算得到强夯有效加固深度随锤径的变化曲线,如图7所示。从图7中可以看到,强夯有效加固深度随着锤径的增加而呈现出先增大后减小的变化趋势。具体表现为:当锤径D<2.0 m时,有效加固深度随着锤径的增加而增加,且锤径每增加0.2 m,有效加固深度增加0.34 m;当D≥2.0 m时,有效加固深度随着锤径的增加而减小,且锤径每增加0.2 m,有效加固深度平均减小0.48 m。由此可知,对换填砂土地基进行强夯加固时,最优锤径为2.0 m。

图7 不同夯锤尺寸下有效加固深度

3.1.4 夯击能组合

保持夯击能3 000 kN·m、夯击次数14次、锤径2.5 m不变,仅改变夯锤重与落距的组合,来分析不同的夯击能组合对强夯有效加固深度的影响。夯击能组合工况设置参数,如表4所示。不同夯击能组合对强夯有效加固深度的影响情况,如图8所示。

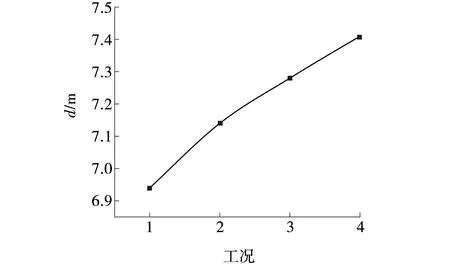
图8 不同夯击能组合下有效加固深度

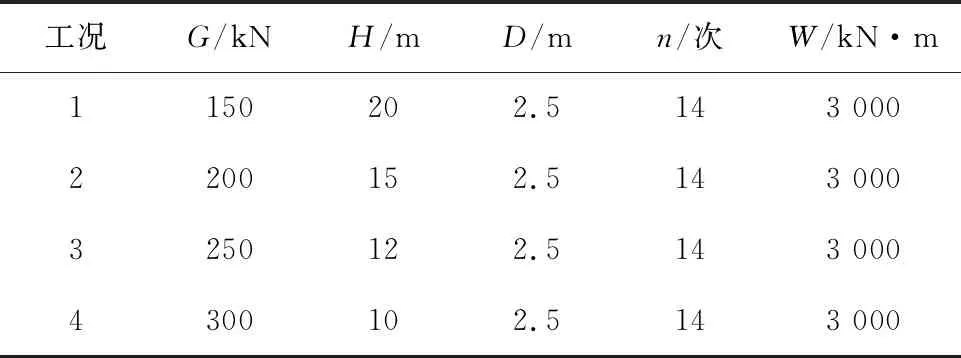
表4 夯击能组合工况参数

从图8中可以看出,当夯击能不变时,随着夯锤重量的增大和落距的减小,强夯有效加固深度基本表现为线性增长趋势。其中,工况1有效加固深度最小,其值为6.96 m。工况4有效加固深度最大,数值为7.42 m,二者的差值为0.46 m。这表明,在夯击能一定的条件下,重锤低落组合比轻锤高落组合的加固效果要好。因此,在施工条件允许的条件下,应优先选择重锤低落施工方案。

综上所述,换填砂土地基强夯有效加固深度受夯击能、锤径、夯击次数及夯击能组合形式的影响均较大,且随夯击能、夯击次数的增大而增大,随锤径(D≥2.0 m)的增大而减小;在夯击能不变的条件下,应优先选取重锤低落施工方案。对于较深厚的换填砂土地基,强夯施工时最优夯击能为3 000～4 000 kN·m,最优锤径为2 m,最优夯击次数为9次。

3.2 土体参数

保持强夯施工参数不变,即夯击能3 000 kN·m,锤径2.5 m,夯击次数14次,夯击能组合工况4,改变单一土体参数来分析其对强夯有效加固深度的影响。

3.2.1 内摩擦角

依据中粗砂内摩擦角的变化范围,分别取换填砂土的内摩擦角为25°、30°、35°、40°四种情况进行对比分析,根据数值计算结果绘制土体内摩擦角对强夯有效加固深度的影响曲线,如图9所示。

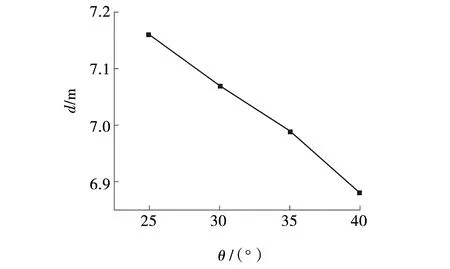
图9 不同内摩擦角下有效加固深度

由图9可知,随着土体内摩擦角的增大,强夯有效加固深度基本呈现出线性减小的趋势,内摩擦角每增加5°,有效加固深度平均减小0.09 m,表明土体内摩擦角对强夯有效加固深度的影响较小。

3.2.2 密度

根据中粗砂的密度变化范围,分别取换填砂土的密度为1 400、1 600、1 800、2 000、2 200 kg/m3五种情况进行对比分析,强夯有效加固深度随换填砂土密度的变化曲线,如图10所示。从图10中可以看到,强夯有效加固深度随着土体密度的增大而呈现线性减小趋势,土体密度每增加200 kg/m3,强夯有效加固深度平均减小0.2 m,表明土体密度的变化对有效加固深度影响较大。

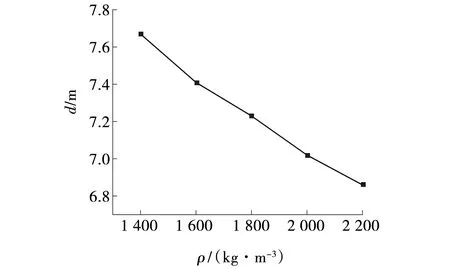
图10 不同密度下有效加固深度

3.2.3 泊松比

根据中粗砂泊松比的变化范围,分别选取换填砂土的泊松比为0.25、0.30、0.35、0.40进行模拟分析,土体泊松比对强夯有效加固深度的影响关系,如图11所示。

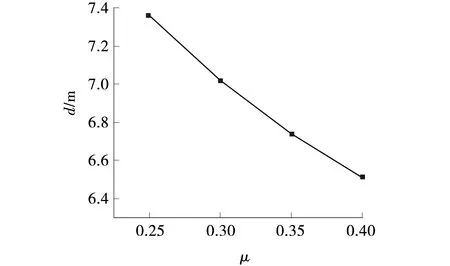
图11 不同泊松比下有效加固深度

从图11中可以看出,随着泊松比的增大,有效加固深度接近线性减小规律,泊松比每增加0.05,有效加固深度整体平均减小0.22 m,表明土体的泊松比对有效加固深度影响较大。

3.2.4 弹性模量

根据中粗砂物理力学参数变化范围,分别选取换填砂土的弹性模量为10、15、20、25 MPa进行对比分析,其对强夯有效加固深度的影响关系,如图12所示。由图12可知,强夯有效加固深度随着土体弹性模量的增大而近似表现为线性减小规律,土体弹性模量每增加5 MPa,有效加固深度整体平均减小0.09 m,表明土体弹性模量对强夯有效加固深度的影响较小。

综上所述,强夯有效加固深度随土体内摩擦角、密度、泊松比、弹性模量的增大而近似呈现线性减小规律。其中,泊松比与密度对有效加固深度的影响较大,内摩擦角与弹性模量对有效加固深度影响较小。