含光伏不确定性的电力系统碳排放流分析
2023-11-15张自强申富泰
张自强,申富泰,魏 军,刘 宁
(甘肃省电力公司,兰州 730050)
0 引言
在“碳中和、碳达峰”的目标下,我国正以低碳创新实现电力行业可持续发展[1-2],以太阳能、风能等为主的新能源发电在电网中所占的比例持续增加,但是将新能源接入电网时,会对电网的碳排放分布产生一定影响,因此,加强新能源接入电网的碳排放分析对发展低碳电力技术具有重要意义[3]。
电力系统碳排放的计算工作是发展低碳电力的基础[4]。目前,电力系统的碳排放计算主要包括宏观统计法[5-7]与碳排放流分析法[8]。宏观统计法根据一段时间的能源消耗总量进行统计,具有计算简便、结果准确的优点,但该方法的不足主要表现为计算过程需要大量区域碳排放数据,且无法精准描述中间环节的碳排放变化过程。碳排放流分析法是一种以电力潮流分布为基础的碳流追踪方法[9],表示为一种依附于电力系统潮流而存在的虚拟网络流,用于表征系统潮流定向移动而产生的碳排放。文献[10]提出将碳排放流概念应用到电力系统中,建立碳流率、碳流密度与碳势指标,并应用到电力系统碳排放流分析中。文献[11]提出潮流分布矩阵、碳流率分布矩阵、碳势与碳排放强度向量等指标,用于分析电力系统碳排放流分布特征。文献[12]定义碳排放流分布因子指标与发电机组关联矩阵,明确碳排放流在电力系统的分布特性与关联机理。文献[13]考虑到传输过程中线路损耗对碳排放计算的影响,提出使用机组注入碳流率、负荷节点碳流率与网损碳流率等指标来建立碳排放流计算方法。上述研究初步建立电力系统碳排放流模型,通过基本的碳流指标,可清晰地展示碳流在电力系统的流向,弥补了宏观统计法计量结果滞后与粗放的缺点。
为分析新能源接入对电力系统碳流分布的影响,后续研究针对具体对象将碳排放流指标进行改进。文献[14]提出荷碳率指标表示储能设备吸收的碳排放量与存储电量的比值,建立含光伏与风电的能源枢纽碳流模型。文献[15]定义发电机组碳排放强度、端口碳排放强度、分支碳排放强度与节点碳排放强度指标,对传统的碳排放强度指标进行细化,建立水电机组接入的电力网络下的综合能源系统碳排放流模型。文献[16]引入碳熵指标描述碳排在能量传递过程中的无序化,建立包含风电、燃煤机组与CHP设备的综合能源系统的碳熵模型,用于简化包含新能源的电力系统下用户碳流计算问题。上述研究将电力系统的风电与光伏的低碳属性用值为0的碳排放强度指标表示,该指标仅反映了清洁能源的物理碳排放值,而无法体现其节碳作用的贡献。因此,需要对原有碳流指标加以改进,以定量评估清洁能源对节能减排做出的贡献。
从碳排放流分析法出发,考虑到光伏出力不确定性的影响,研究光伏电场集中式与分布式接入电力系统的碳排放流问题。首先,建立光照强度与系统节点总碳流率的函数表达式,使用节点碳势与支路碳流率分析系统碳排放流的变化;其次,计算路径输出分布因子矩阵,取得系统碳排放流路径信息与各节点碳排放流分布特性;最后,将光伏出力不确定性转移到平衡机组出力变化,计算光伏电场集中式与分布式接入的节点与支路碳流率影响因子,进而定量分析光伏发电对电力系统的碳减排效果。
1 电力系统碳排放流相关指标
碳排放流分析法的基本指标包括节点碳势与支路碳流率,分别表示碳排放流在电力系统各支路的具体流向与各节点的碳排放强度,不足以描述光伏接入对电力系统碳排放流分布产生的具体影响。因此,在基本指标基础上提出总碳流率与碳流率影响因子指标。
1.1 支路碳流率
碳流率表示单位时间内经过系统节点或支路的碳排放量E,单位t(CO2)/h,碳流率R可表示为:
(1)
支路碳流率表示单位时间内流过支路的碳排放量。而在实际计算过程中,由于碳排放量一般是未知的,因此计算方法参考支路碳流密度等于该支路起始节点碳势性质[4],支路号为s的碳流率Rs表示如下:
Rs=PBsρs=PBseN0
(2)
式中:PBs为支路s的有功功率;ρs为支路s的支路碳流密度;eN0表示支路s的起始节点碳势。
1.2 节点碳势
节点碳势用于表示该节点消耗单位电量等效在发电机组释放的碳排放量[11],单位kg(CO2)/(kW·h),节点i的碳势eNi表示如下:
(3)
式中:N+为有功潮流流入节点i的所有支路的集合;s为支路号;PGi为节点i连接的发电机组有功功率;eGi为节点i连接的发电机组碳排放强度。
1.3 系统总碳流率
系统总碳流率表示电力系统所有节点碳流率总和,即所有机组注入网络的总碳流率,单位 t(CO2)/h,可表示为:

(4)
式中:n为电力系统节点数;Rall为电力系统节点碳流率总和;Ri为节点i的碳流率;PGi为节点i的发电机组输入有功功率;eGi为节点i的发电机组碳排放强度。
1.4 碳流率影响因子
影响因子可分为节点与支路碳流率影响因子。节点碳流率影响因子表示各机组对某节点碳流率的贡献,该因子受发电机组碳排放流注入量和接入系统位置的影响。支路碳流率影响因子表示某台发电机组的碳流注入系统的所有支路碳流率的贡献情况。使用平衡机组的碳流率影响因子等价于光伏机组对电力系统降碳贡献,影响因子越低,表示光伏机组对节点或支路的低碳贡献越高。
2 含光伏电力系统碳排放流分析
由于碳流分析注重碳排放流的总排放量与系统的各环节分布量,因此针对含光伏的电力系统碳排放流的分析将围绕上述2个方面展开,建立系统总碳流率与碳流率影响因子指标描述光伏发电对系统的影响。
2.1 含光伏的电力系统总碳流率计算
考虑到光伏发电系统出力的随机性与波动性源于光照强度的不确定性,为此先建立光照强度与电力系统节点总碳流率之间的函数表达式:
Rall=f(r)
(5)
式中:f(r)为光照强度与系统节点总碳流率的函数表达式。
光伏电站由多个光伏阵列组成,且光照强度是导致光伏阵列出力变化的主要影响因素,暂不考虑其他影响因素。若暂不考虑光伏发电功率损失,可认为光伏发电注入系统的有功出力即为光伏电场中所有光伏阵列的有功功率之和,光伏电场输出功率表达式为[17]:
PW=PMN=rAηN[1-0.005(t0+25)]
(6)
式中:r为光照强度;A为光伏阵列面积;η为光电转换效率;N为光伏阵列数量;t0为大气温度。
电力系统碳排放流与光伏发电系统的有功出力相关,而受无功出力影响微小。此处假设只考虑光伏电场的有功出力,忽略光伏电场注入无功功率。通过对电力系统进行直流潮流计算,得到连接常规发电机组的节点注入有功功率:
Pi=PGi-PLi
(7)
式中:Pi为节点i的注入有功功率;PGi为节点i的发电机组输入有功功率;PLi为节点i的有功负荷。
基于式(6)和式(7)的研究,光伏发电系统连接到节点j注入的有功功率为:
Pj=PW-PLj=
rAηN[1-0.005(t0+25)]-PLj
(8)
式中:Pj为节点j的注入有功功率;PLj为节点j的有功负荷。
在直流潮流计算中,忽略无功功率与系统网络损耗,平衡节点s出力等于其他所有节点出力之和的逆值:
(9)
式中:PGs为平衡节点s的发电机组注入有功功率。
电力系统的节点总碳流率等于平衡机组与其余发电机组一定时间内碳排放强度与有功功率乘积之和,即:
(10)
式中:PGk为节点k的发电机组输入有功功率;eGs和eGk为平衡机组和其余机组的碳排放强度。
联立上述所有等式,得到关于光照强度与系统节点总碳流率的函数表达式:
rAηN[1-0.005(t0+25)]-PLj)+
(11)
由式(11)可知,节点总碳流率与光伏电站的输出功率、各节点注入有功功率与常规发电机组碳排放强度相关。
2.2 含光伏的碳流率影响因子计算
含光伏的碳流率影响因子计算过程主要包括建立影响因子表达式与通过有向通路算法计算路径输出分布因子矩阵2个方面。
2.2.1有向通路算法
为计算碳流率影响因子,需先找出电力系统任意2节点间的所有有向通路,目前已有不少关于这方面的算法[18-19],由于有向通路算法不受有向图的并行边限制,是一种易于实现、实用性很强的算法。因此基于文献[20]有向通路算法完成计算,其基本原理如下:
设有向通图G=(V,E),|V|=n:
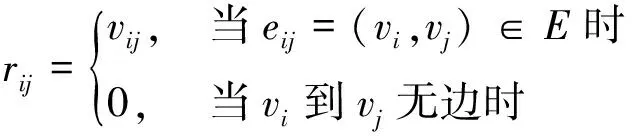
(12)
n阶方阵R=[rij]表示了有向图中每条边的终点,称其为邻接终点矩阵。
作顶点集V的v-1个子集Vi(i=1,2,…,v-1)序列,使得V⊃V1⊃V2⊃…⊃Vn-1,每个子集的元数为|V|=v-i(i=1,2,…,v-1)。对于每个子集Vi,对应的有一个矩阵R(i)=[r(i)ik],它由R(i-1)(R(0)=R)递推而得:如果Vi-1-Vi={vx},则第i次去掉的节点为vx,则
(13)
式中:“*”表示元素的毗连,用来表示顶点的序列,它满足结合律,但不满足交换律;“+”表示条件“或”,它满足结合律、交换律及2种运算间的分配律。
0 +vi*…*vim=vi1*…*vim+ 0=
vi1*…*vim
(14)
0*vi1*…*vim=vi1*…*vim0=0
(15)
式中:在项vi1*… *vim中,若其中任一顶点重复出现,则该项为0。
从矩阵R(i)可得:若r(i)ik≠0,且j≠k,则r(i)ik表示从顶点vi到vk的全部有向通路。
2.2.2基于有向通路算法的碳流率影响因子计算
1) 节点与支路碳流率影响因子计算
在随机直流潮流计算中,假设光伏机组有功出力的波动由平衡机组承担,即:
ΔPW=ΔPGs
(16)
平衡机组目的是用于平衡部分未知的功率损耗,承担由功率损耗引起的功率波动与实现系统的功率平衡。此处,将光伏机组有功出力的改变对系统碳流率的影响等效为平衡机组碳流率的变化,光伏机组注入有功功率对系统碳流率的改变,也可由平衡机组出力变化对系统各部分的影响代替。
由文献[12]可知机组-节点碳流率关联矩阵RU-N与机组-支路碳流率关联矩阵RU-B的计算模型,进一步得到平衡机组-节点碳流率关联向量RUs-N为:
(17)
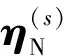
设JUs-N为平衡机组-节点碳流率影响因子向量,即:
(18)
平衡机组-支路碳流率关联矩阵RUs-B的计算过程如下:
(19)
则平衡机组-支路碳流率影响因子关联向量JUs-B为:
(20)
由以上分析可知,平衡机组的碳排放强度、电力系统拓扑结构与电力系统运行的潮流分布等因素共同决定光伏机组对系统节点与支路的碳流率影响因子。
2) 路径输出因子矩阵计算
路径输出分布因子是计算碳流率影响因子的关键矩阵[12],由于碳排放流路径输出分布因子与有功潮流路径输出分布因子相等,通过有向通路算法计算有功潮流的路径输出分布因子矩阵,计算过程如下:
路径输出分布因子矩阵D,表示在路径i-j之间从起始节点i流出的有功潮流对流入目标节点j的全部有功潮流的占比[12]。由上述定义可知,矩阵中的对角元素值等于1,即:
Dij=1,i=j
(21)
对于矩阵的非对角元素计算,首先定义一个辅助矩阵,即支路输入分布因子矩阵G,用于描述在支路i-j之间的有功潮流与流入起始节点i的有功潮潮流总量的比值,则:
(22)
式中:H、I、PN、PB分别为节点输出分布因子矩阵、单位矩阵、节点有功通量矩阵与支路潮流分布矩阵[5]。
计算节点i-j之间的路径输出分子因子Dij,设G(x) (i,j)是对G进行变换后的N-x维子方阵,(i,j)为节点坐标,x=1,2…,N-1,共有N-1个子方阵。
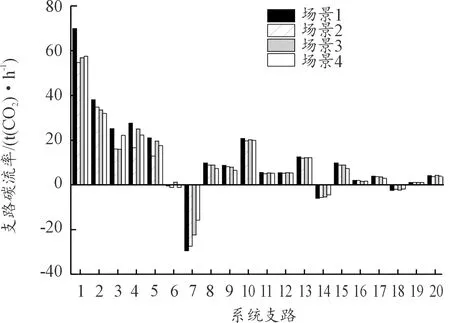
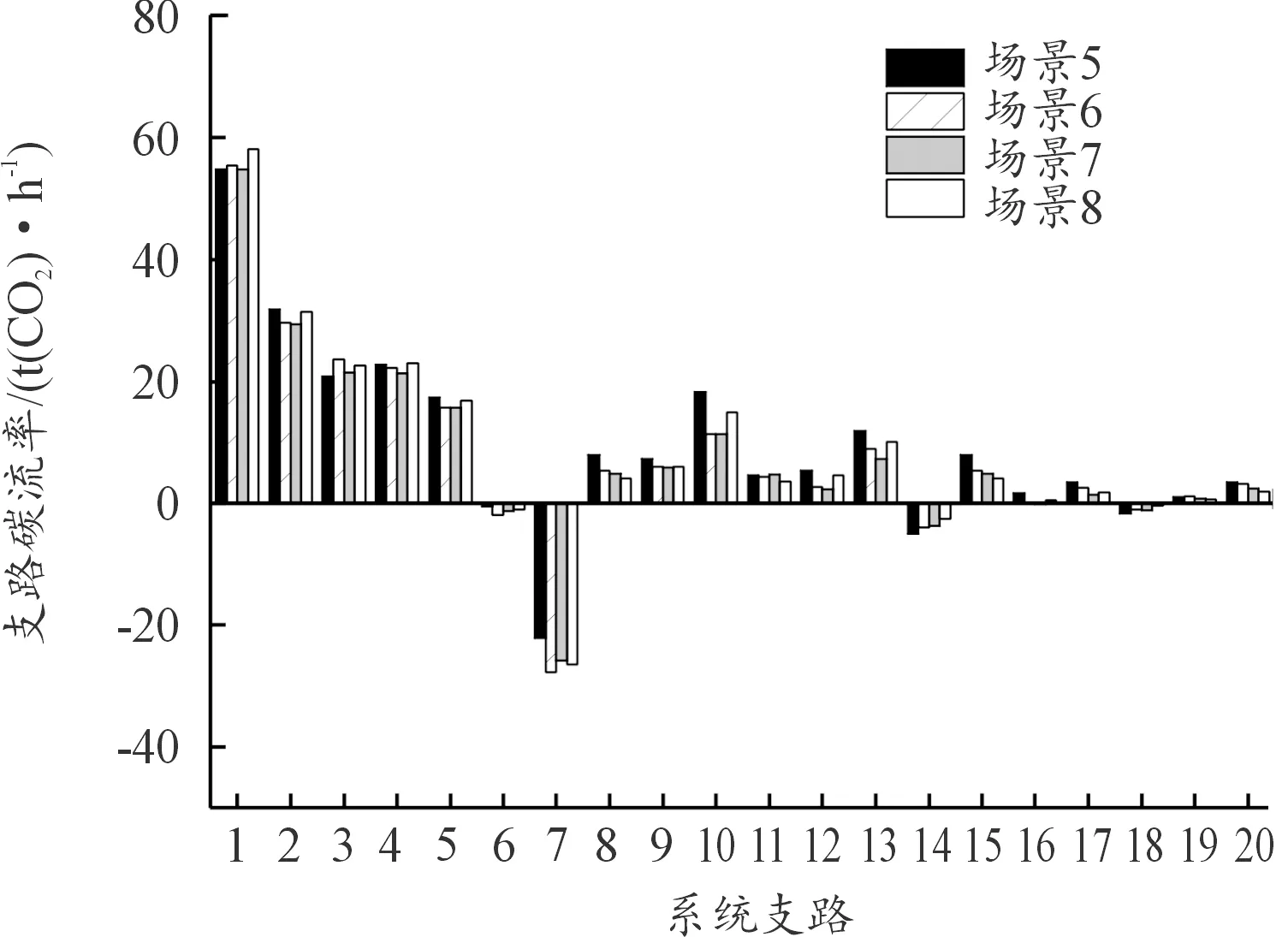
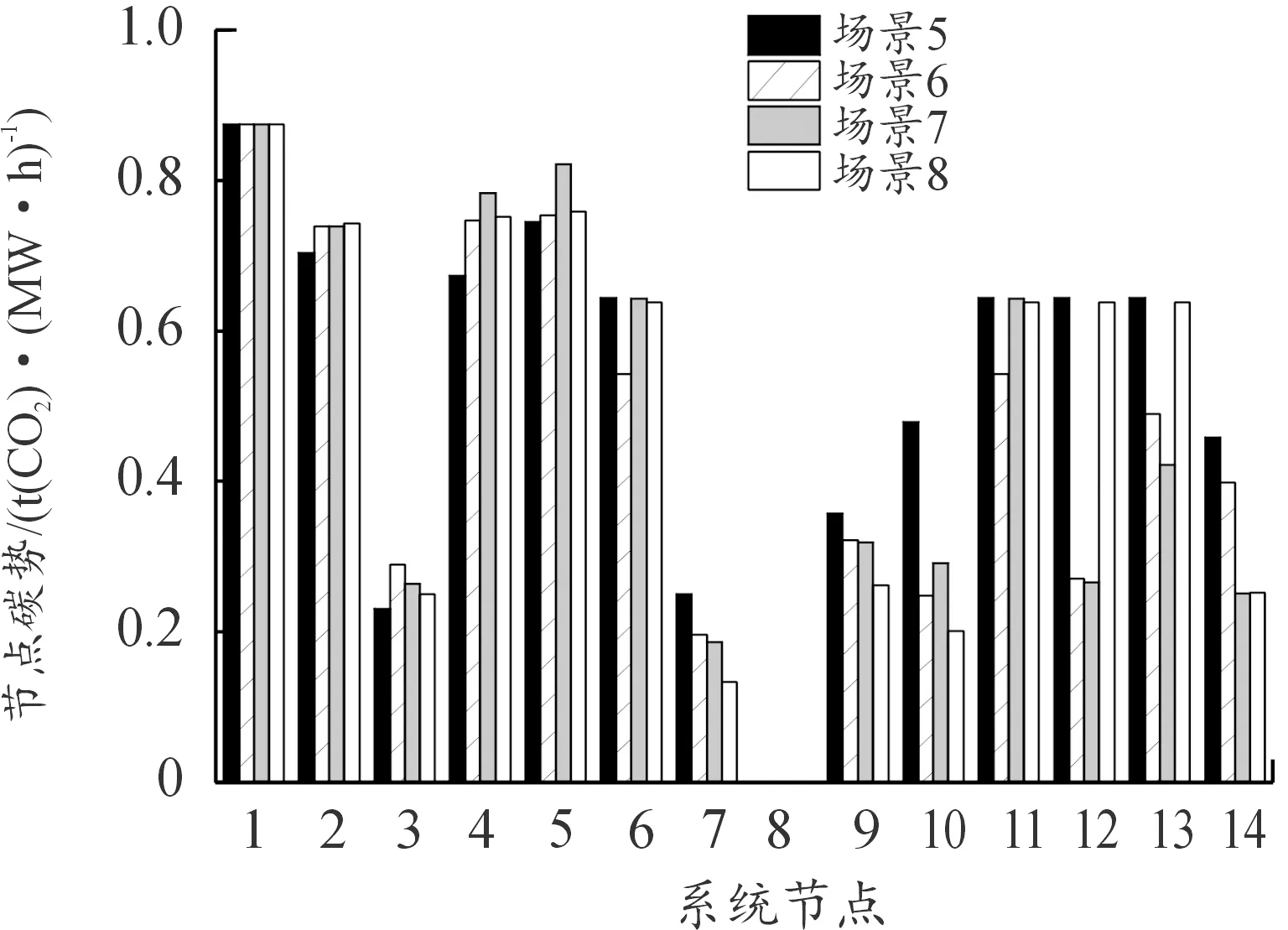
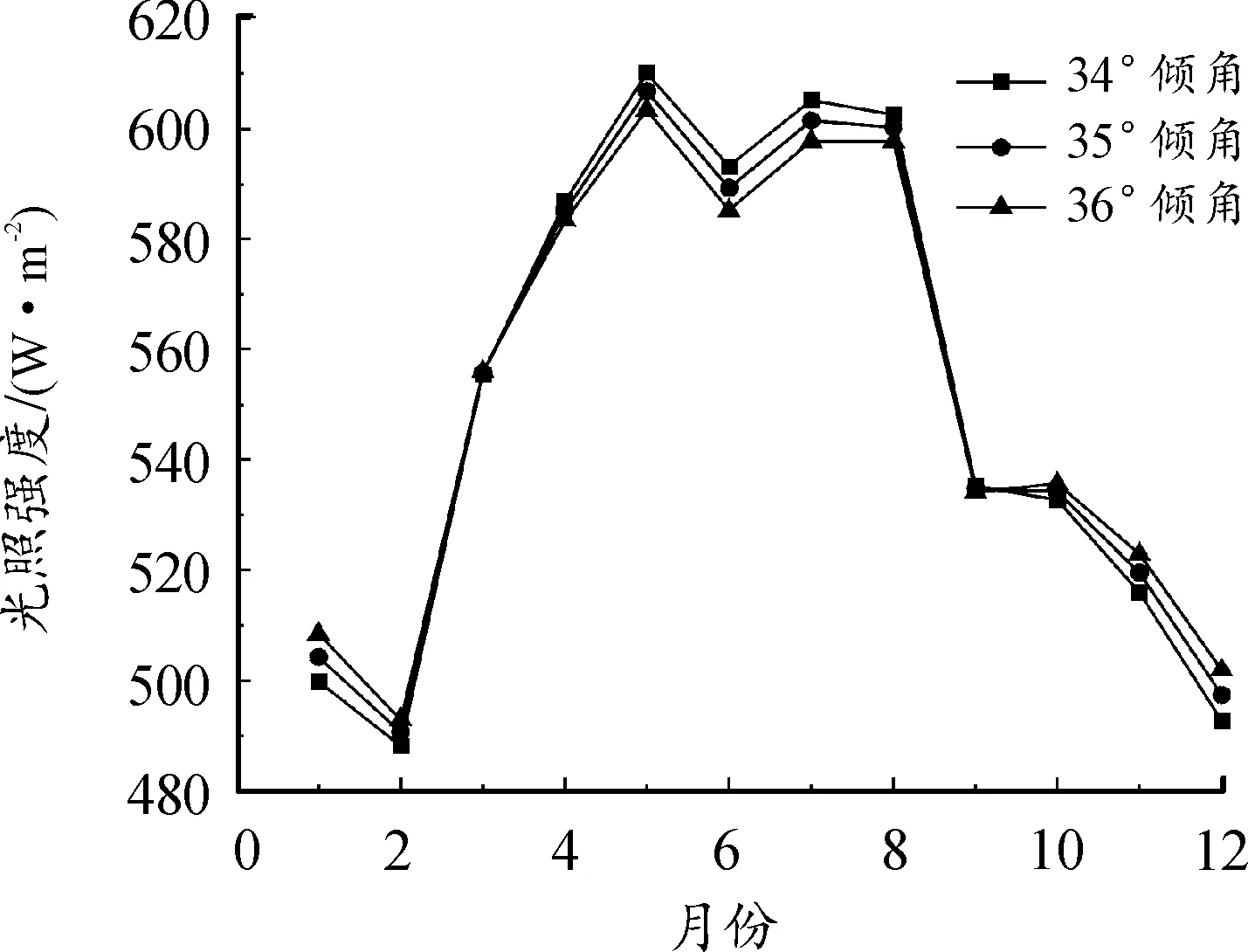
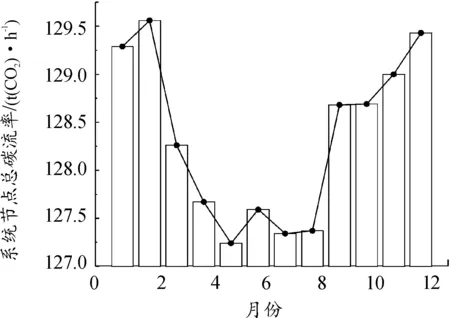
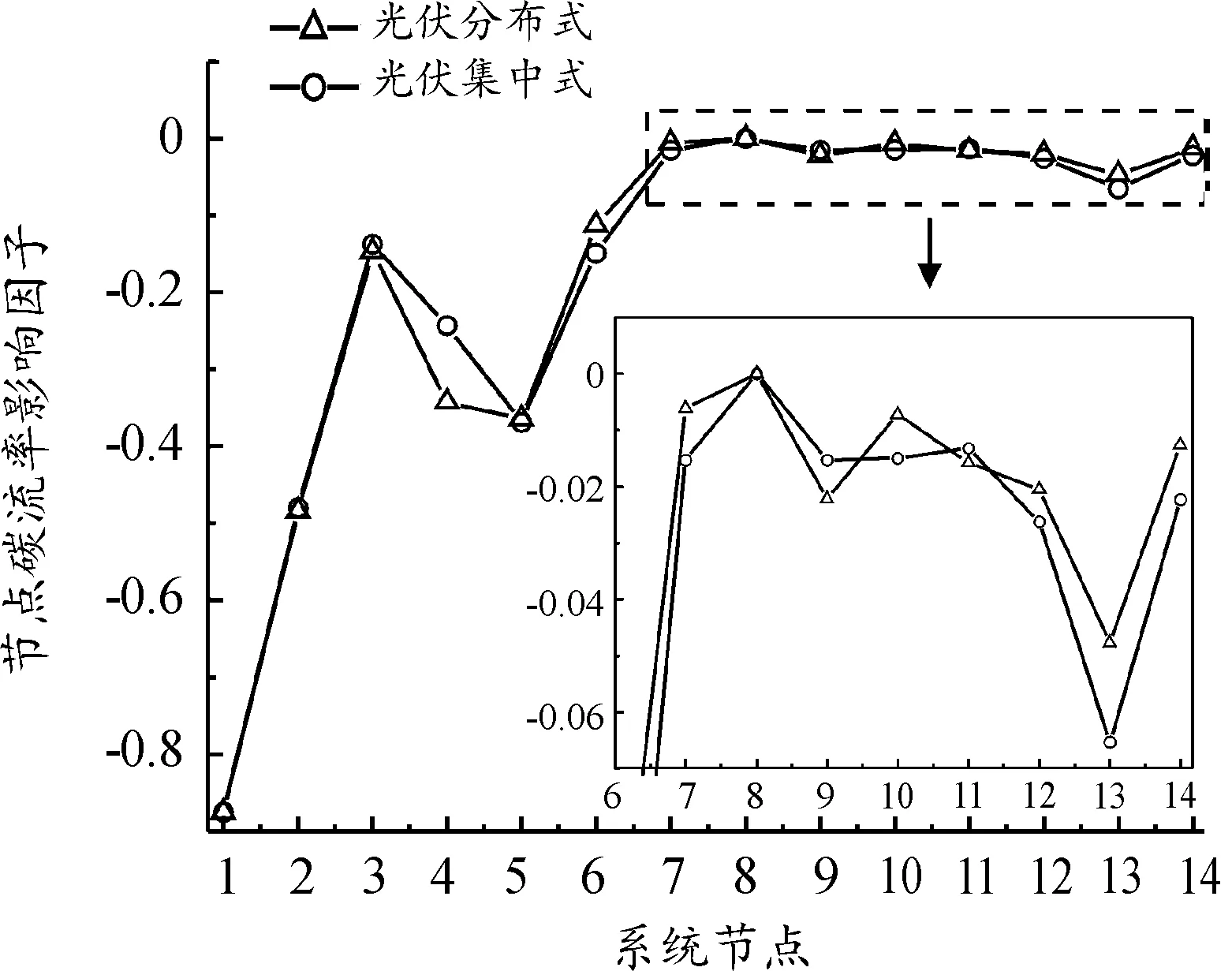
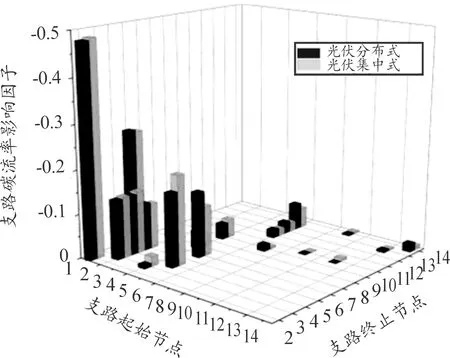
首选对G(x) (i,j)的元素进行变换得到G(x) (i,j)′。当x (23) 式中:r和s分别为矩阵的行号和列号。 当x=N-2时,矩阵G(N-2) (i,j)为二维方阵。此时,可以根据下式得到Dij的值: (24) 对此,矩阵D的元素表达式为: (25) 选取IEEE14节点系统进行算例分析,在不计网损的情况下,系统潮流分析使用直流潮流法计算,单位均为MW,未接入光伏时系统稳态有功潮流分布如图1所示。选取甘肃某地实测全年光照强度,设置额定容量为20 MW的光伏电场,光伏电场参数设置如表1所示。将光伏电场以集中式与分布式接入IEEE14节点系统,分布式接入节点的光伏电场容量均为5 MW,设置8种不同光伏电场接入场景如表2所示。 表1 光伏电场参数设置 表2 光伏电场接入场景 图1 IEEE14节点系统稳态潮流分布 设置系统各发电机组碳排放强度单位为kg(CO2)/(kW·h),G1为燃煤机组,G2和G4为燃气机组,G3和G5为水电机组(水电不属于新能源机组,将该机组出力设为定值,其不影响光伏接入系统的碳排放分布)。机组碳排放强度EG如下所示: (26) 光伏电场集中式与分布式接入电力系统的各支路碳流率分别如图2和图3所示。其中,因为部分支路中经过逆向潮流,导致支路碳流率为负值。场景7的支路碳流率总值在8种场景中最低,为220.68 t(CO2)/h,相比场景1降低27.29%,可使系统保持更低的碳流率分布状态,即单位时间系统各支路碳排放总量更低。 图2 集中式接入的系统各支路碳流率 图3 分布式接入的系统各支路碳流率 光伏电场集中式与分布式接入电力系统的各节点碳势分别如图4和图5所示。由图4可知,光伏接入节点2、3、4的碳势与场景1相比明显降低,其余节点由于未接入光伏电场降幅不明显,表明集中式接入具有直接改变接入节点碳势的能力。由图5可知,光伏分布式接入节点的碳势降幅不如集中式明显,但都低于场景1的碳势值。由场景6的节点11、13与场景7的节点7、9可知,分布式接入会使接入节点的周边节点碳势降低。对比可知场景6在8种场景中节点碳势总值最低,为6.415 t(CO2)/(MW·h),相比场景1降低20.80%。 图4 集中式接入的系统各节点碳势 图5 分布式接入的系统各节点碳势 甘肃某地全年月平均光照强度与35°倾角下的系统节点总碳流率分别如图6和图7所示。 图6 全年月平均光照强度 图7 35°倾角下系统节点总碳流率 由图6可知,光伏组件不同倾角导致所接受的光照强度不同,在35°倾角下光照强度平均值最高。光照强度的波动影响光伏机组出力,间接使得系统节点总碳流率也具有波动性。由图7可得到验证,在4—8月光照强度较高时,系统节点总碳流率在全年中保持较低水平。 晴天与阴天的光照强度和系统节点总碳流率如图8所示。考虑到气候因素对光伏发电出力不确定性的影响,选取甘肃某地时间为7∶00—20∶00的晴天与阴天光照强度,计算其一天内的系统节点总碳流率。由图8可知,晴天光照强度高,光伏机组出力多,系统消纳更多的光伏出力,因此电力系统节点总碳流率随之减少,同理阴天与之相反,结果验证了式(11)的合理性。 图8 晴天阴天光照强度和总碳流率 由图9可知,因平衡机组G1并无潮流流向节点8,因此无论光伏集中接入还是分布接入,其对节点8的碳排放流的贡献为0。光伏集中式接入下节点4的碳流率影响因子绝对值为0.243 4,与分布式相比降低最为明显,因为节点4注入的光伏有功出力消纳部分有功负荷,该节点从系统中吸收的有功功率降低,即机组G1发出的有功功率流入该节点的含量降低,最终导致机组G1节点4的碳流率影响因子降低。同理由于分布式光伏接入容量较小,导致接入节点5、7、10、14的影响因子相比集中式降幅不明显。 图9 光伏接入的节点碳流率影响因子 以场景4与场景8的接入方式与接入位置为例,由式(20)计算光伏电场对于系统各支路的碳流率影响因子,支路碳流率影响因子如图10所示。 图10 光伏接入的支路碳流率影响因子 由图10可知,光伏集中式接入节点4的支路4-3与2-4碳流率影响因子相比分布式降低,但支路4-3的降幅更大。由式(20)可知,支路4-3的碳流率影响因子由平衡机组碳排放强度eGs、路径输出分布因子D14与节点输出分布因子H43计算得到,eGs为恒定值暂不考虑,因此光伏机组接入节点4,节点1流向节点4的各条路径中的有功潮流减小,同时由于系统有功潮流分布因素,流过支路 4-3的有功潮流更小,最终使得支路4-3的碳流率影响因子降幅更大。通过三维直方图可以更加直观分析光伏电场集中式与分布式接入对系统支路碳流率的具体影响。 1) 提出考虑光照强度不确定性的电力系统碳排放流分布分析方法,得到光照强度与系统节点总碳流率的函数表达式,将确定碳排放流分析延伸到不确定分析环境。 2) 通过节点碳势与支路碳流率分析光伏接入系统节点与支路碳排放流分布变化,建立8种不同光伏接入场景,对比无光伏接入场景,分布式接入场景6的碳势总值、场景7的支路碳流率总值分别降低20.80%与27.29%。 3) 通过有向通路算法计算光伏注入功率影响系统的节点与支路碳流率影响因子,进一步考虑不同接入方式时光伏注入功率对系统碳排放流分布特征的影响。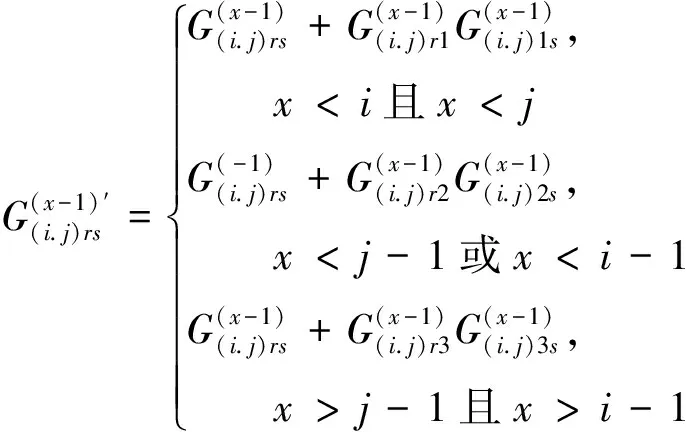
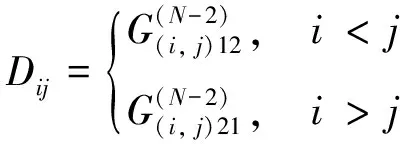
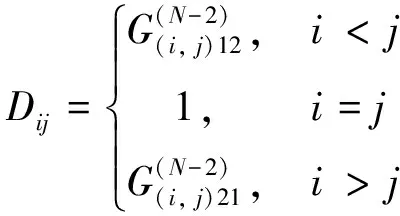
3 算例分析

3.1 支路碳流率与节点碳势

3.2 系统总碳流率与碳流率影响因子

4 结论
