FSAE赛车弯道气动特性数值模拟与试验研究
2023-11-15赖晨光刘丽华温世豪翟光涛
赖晨光,刘丽华,冯 帅,温世豪,翟光涛
(重庆理工大学 车辆工程学院,重庆 400054)
0 引言
大学生方程式比赛简称为FSAE(Formula SAE),于1978年由美国汽车工程学会(SAE)举办,是一项由学生自主设计、制造与测试一辆小型单座开轮式赛车的比赛。合理的气动设计可以为赛车产生下压力,以提高其在弯道中的速度。因此,气动设计是FSAE赛车的重要环节之一。在动态赛中,弯道众多,赛车大部分时间均处于弯道工况。赛车在弯道中气动力与气动力矩均会发生改变,从而影响赛车在极限条件下的操纵稳定性。因此,在FSAE赛车气动设计中仅考虑直道工况较为不妥。
从20世纪60年代开始[1],空气动力学套件就被应用于赛车以提高操纵稳定性。FSAE赛车与一级方程式赛车均属于开轮式赛车,因此具有较为相似的气动布局。FSAE赛车平均时速约60 km/h,但气动套件对FSAE赛车性能具有很大提升,这一点已经得到了Wordley等的验证[2]。他们研究了FSAE赛车在直线加速、八字绕环(skid pad)、高速避障和耐久赛等不同动态项目中加装倒置翼片的效果,表明加装了倒置翼片的FSAE赛车在直线加速所用时间更长,但在其他动态赛中与没有安装倒置翼片相比具有很大优势。
有学者利用计算流体力学(CFD)方法对赛车在弯道处的空气动力学特性进行了研究。Douglas等[3]考虑了横摆角对赛车气动性能的影响,发现偏航时翼片端板对下压力有不良影响,特别是横摆角较大时。Watanabe等[4]提出了一种新的方法——移动计算域(moving computational domain,MCD)来模拟高速汽车通过发夹弯的情况。Tsubokura等[5]对车辆动态转向时的气动力进行了研究,指出高速转弯时产生的不稳定气动力会影响汽车的稳定性。Nara等[6]用移动计算域的方法对方程式赛车进行了弯道模拟,模拟了赛车在富士赛道上行驶,并解释了在滑移角和速度变化上存在气动力差异的原因。Keogh等[7]提出了分析弯道中车辆空气动力学方法,数值模拟中需要模拟车辆周围呈现曲率运动的流场情况,并指出沿弯道径向的流速会呈梯度变化。还通过数值方法研究了Ahmed模型在弯道中的空气动力学,观察到偏航力矩引起的气动力和不对称尾迹的变化[8]。Sagmo等[9]对FSAE赛车的弯道空气动力学进行模拟,研究了弯道工况与横摆工况相比气动力变化,发现稳态弯道工况与横摆角之间的流场存在差异。Patel等[10]研究了多元倒置翼片的弯道和地面效应时的气动特性,发现了涡轨迹变化。Nakashima等[11]对Ahmed模型的弯道气动特性进行了研究,发现了气动阻力增加和气动力矩的产生。Piechna等[12]通过数值模拟和道路实验研究了主动式气动部件在转弯时的性能。宋世达[13]通过仿真研究了不同工况下的气动性能差异,探究了各气动装置对整车性能的影响。梁德慧等[14]利用场函数方法实现了对FSAE赛车稳态弯道的仿真。
以往对于弯道空气动力学研究大多集中在过弯模拟,缺乏对弯道过程中流场分析。近年来,赛车空气动力学设计日趋复杂,越来越多工况被纳入考虑范围之内,因此,需较为深入的研究赛车在弯道处流场变化细节,以更好地理解弯道工况中气动力变化。笔者在前人研究的基础上,通过数值仿真研究FSAE赛车在弯道工况中流场变化导致气动力变化的原因。重叠网格被证明是一种较好的模拟运动物体的方法,目前应用广泛[15-19],因此,本研究选择重叠网格来模拟FSAE赛车匀速过弯工况。本研究可为开轮式赛车的空气动力学设计提供指导意义。
1 数值仿真
1.1 空气动力学模型
为保证本研究普适性,建立一简化FSAE赛车模型。如图1所示,它具有FSAE赛车大部分特征,并符合FSAE赛事规则,在该模型中忽略悬挂杆系,并简化后舱与座舱等区域。该模型主要由前翼、车身、尾翼、车轮和扩散器组成。模型基本几何参数如表1所示。
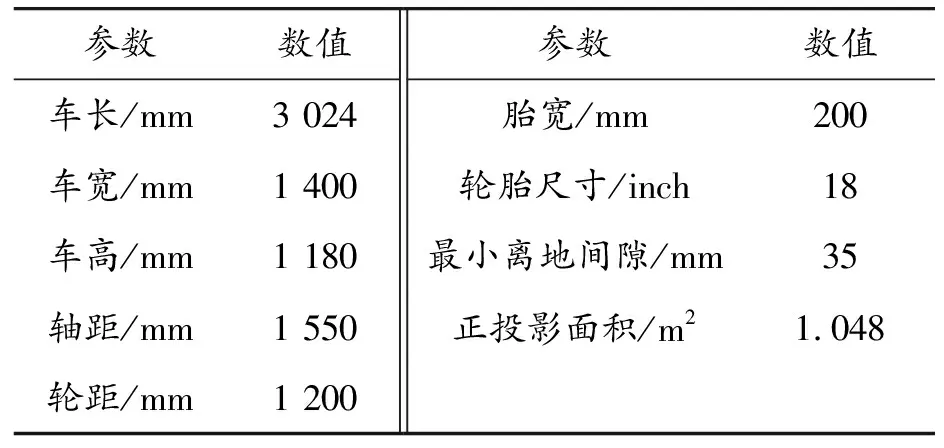
表1 FSAE模型基本几何参数
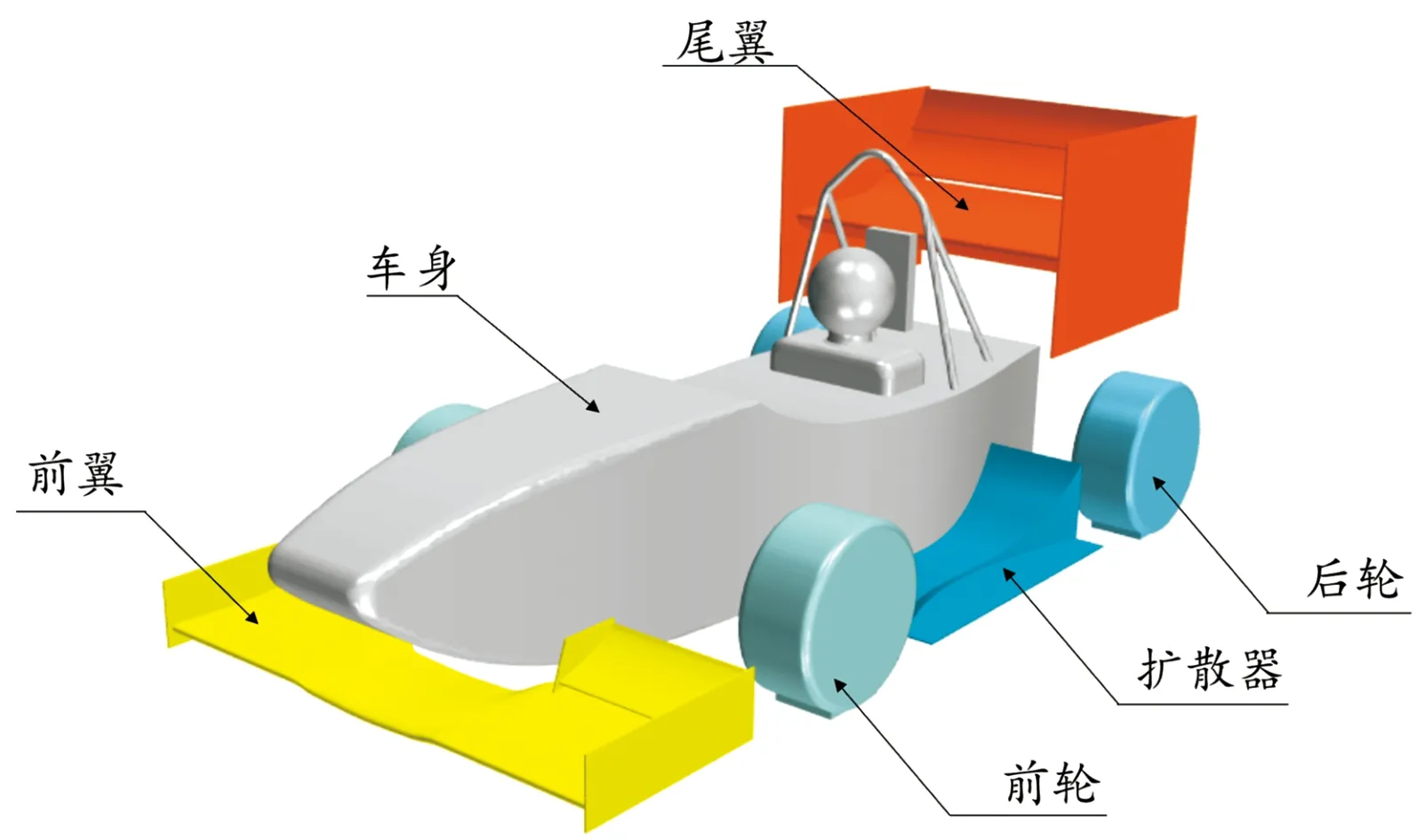
图1 FSAE赛车模型
1.2 直道与弯道工况边界条件
为保证仿真一致性,在直道和弯道工况下均采取重叠网格方法。直道工况计算域尺寸与边界如图2所示。直道工况计算域宽约模型宽11倍,高约9倍,阻塞比约0.63%。由于拟模拟时间为2 s,计算域长度应大于2 s的运动距离,考虑空气黏度对边界的影响,故计算域长度为36 m。计算域两端设有压力出口,允许气流进出,其他边界为壁面。如图3所示为直道工况重叠网格边界,重叠网格由背景域、重叠域和交接面组成,FSAE赛车运动速度为15 m/s。
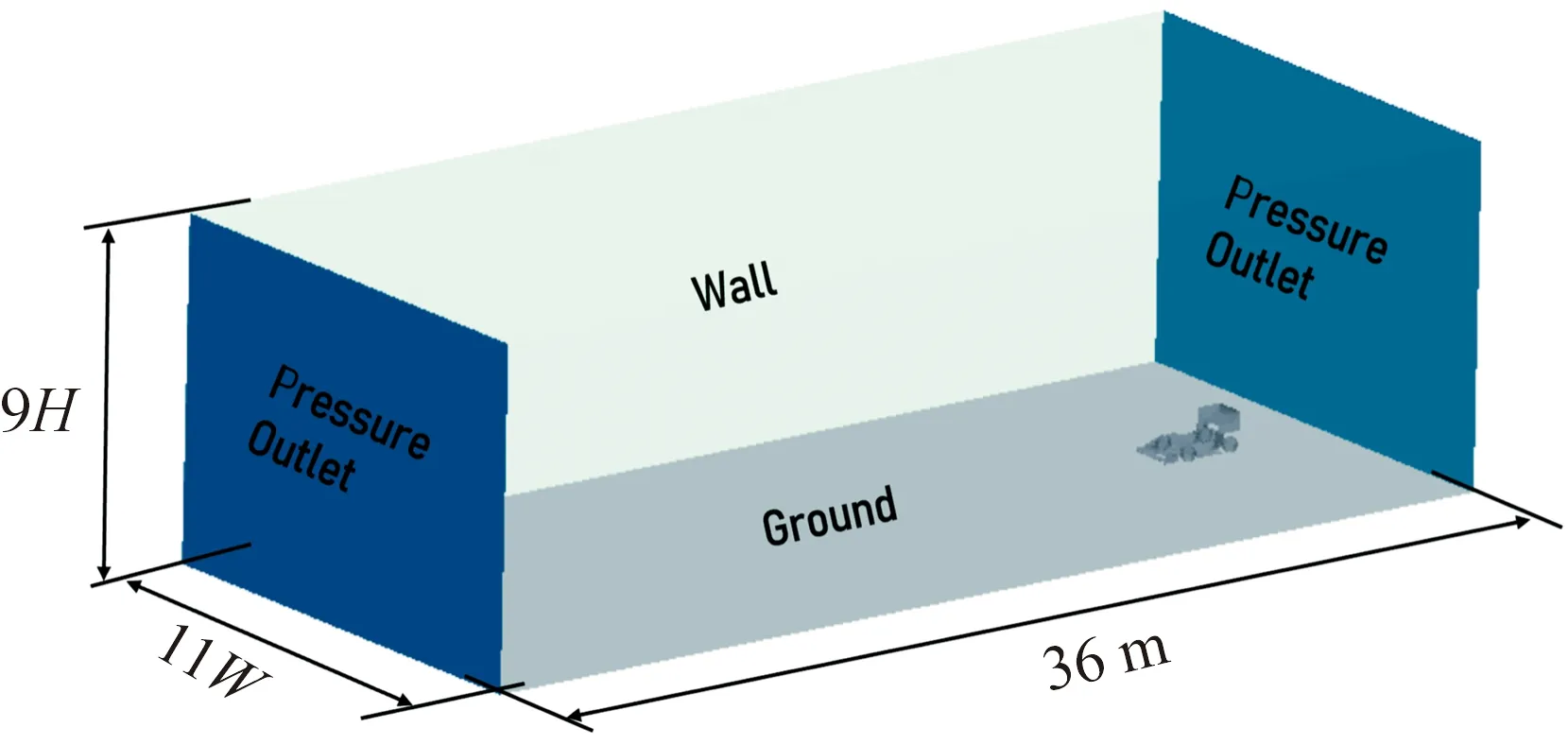
图2 直道工况计算域尺寸与边界
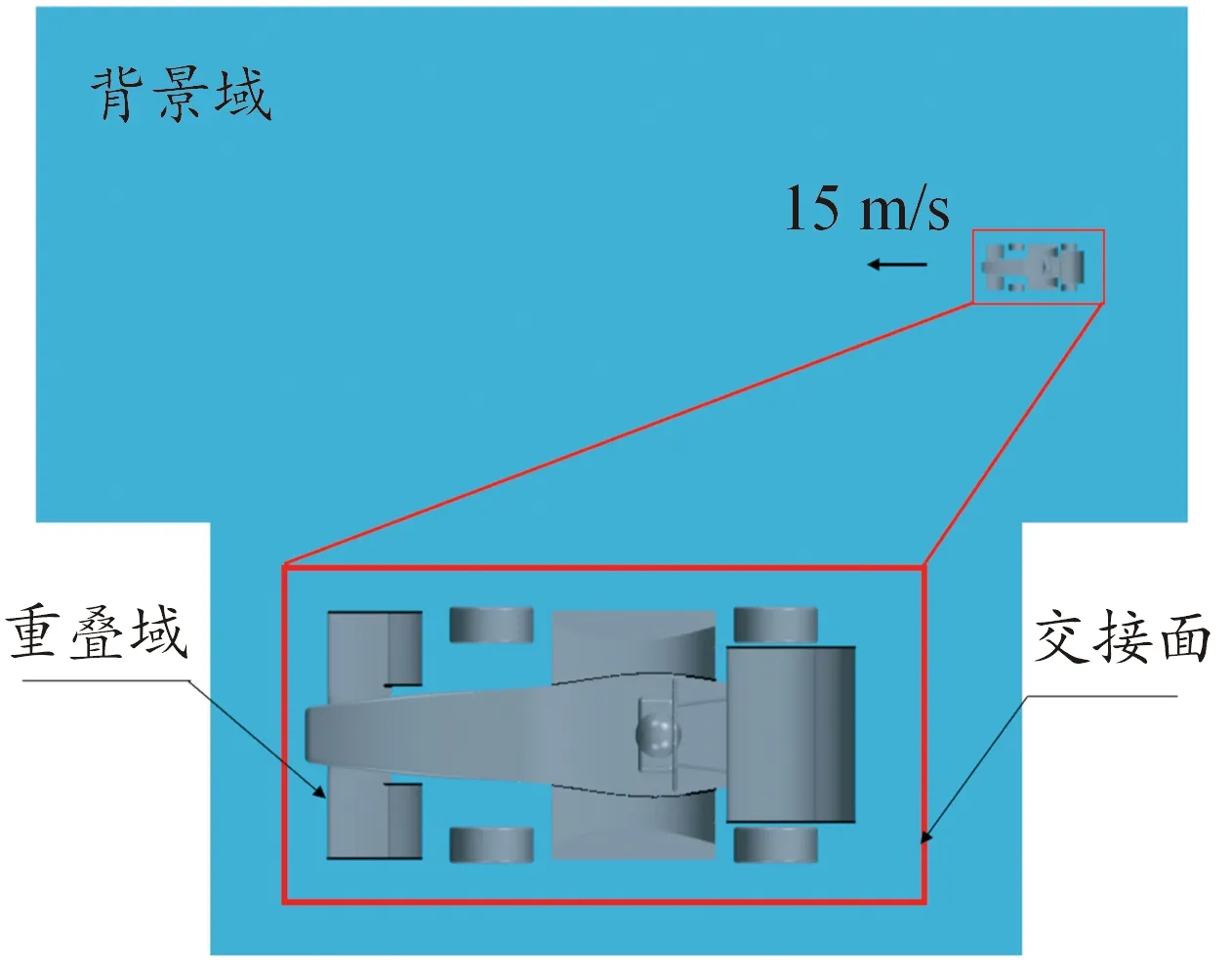
图3 直道工况重叠网格边界
弯道工况计算域如图4所示,宽度和高度约为模型宽度的8倍,高度的7倍,阻塞比约1.2%。计算域内半径为5 m,计算域外半径为15 m,因此转弯半径为10 m。边界条件与直道保持一致。图5为弯道工况下重叠网格边界,背景区域为圆形弧线,运动速度为15 m/s,轨迹沿虚线所示半径为 10 m的曲线运动。

图4 弯道工况计算域
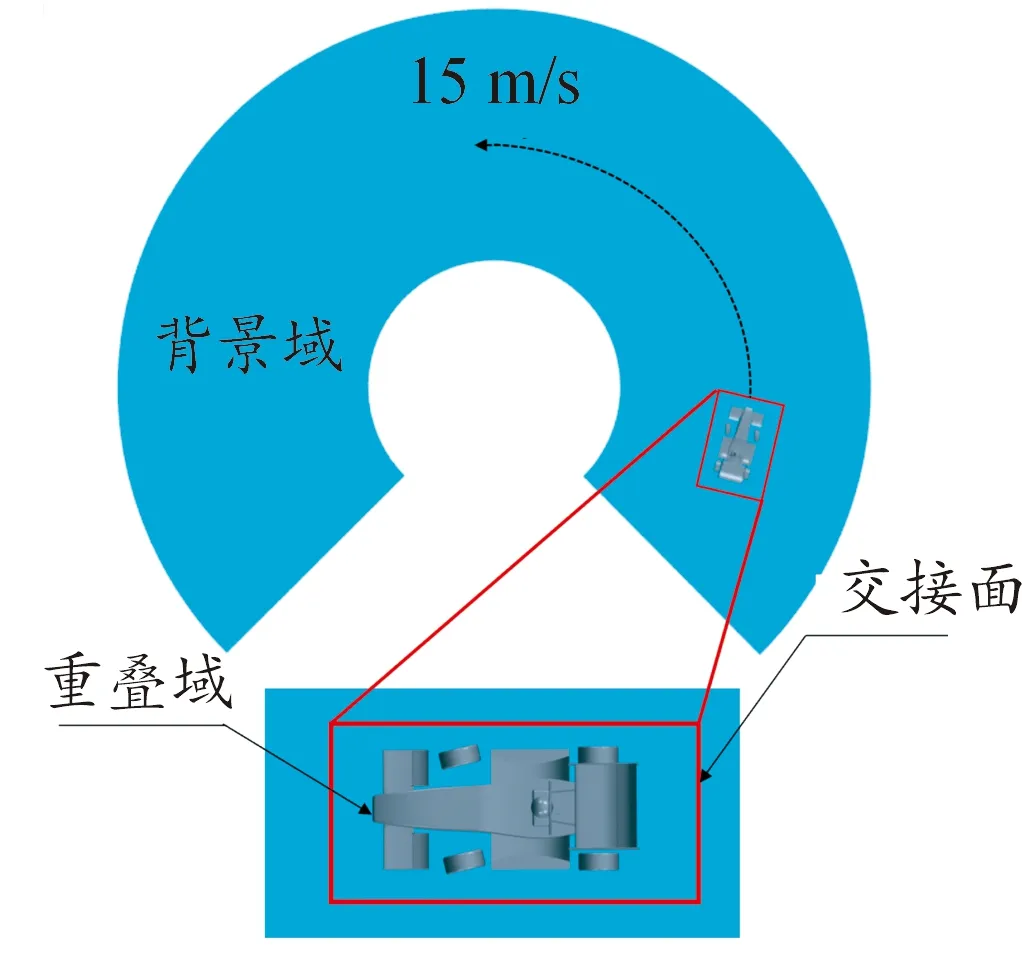
图5 弯道工况重叠网格边界
1.3 车身姿态
前轮转角是一个不可忽视的因素。在忽略车轮侧偏角情况下,转弯时前轮转角为:
δ=arcsin(L/R)
(1)
式中:L为轴距;R为弯道半径。算出无侧偏角下前轮转角为8.9°。
赛车在极限条件下具有较大的轮胎侧偏角,导致前轮需要更大转向角[20]。根据FSAE轮胎的特性和弯道条件[21],侧偏角取值为4°。忽略阿克曼角,因此总转向角为12.9°。默认赛车处于中性转向,忽略俯仰角和横摆角,侧倾角为2°。因此FSAE赛车在弯道中的姿态如图6所示。
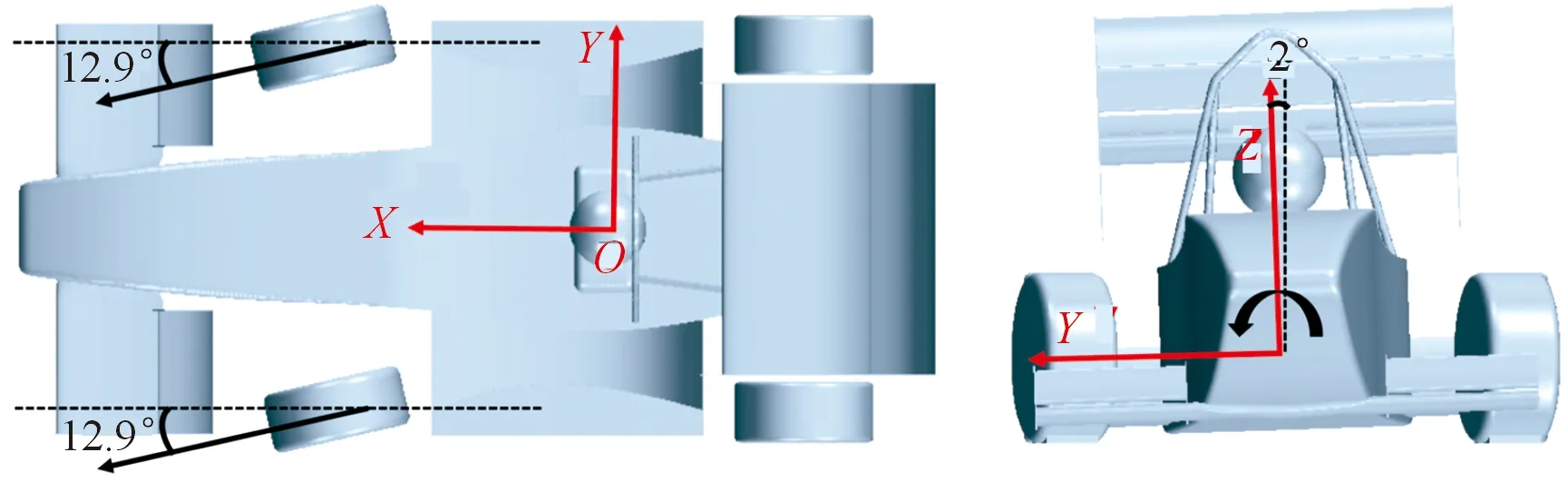
图6 弯道工况中的姿态
1.4 网格
此模型几何较为复杂,采用非结构化网格可以更好地贴合表面。利用ANSA软件进行几何处理和曲面网格划分。为平衡计算精度与速度,将曲面划分不同面网格尺寸,如表2所示。为捕捉翼片边界层流动细节,翼片表面具有最小的表面网格尺寸。直线工况和弯道工况具有相同的表面网格尺寸以保持一致性。

表2 面网格尺寸
由于SSTk-ω湍流模型对壁面要求,需要更多网格来捕捉壁面附近边界层的流动。因此,壁面y+值约为1。棱柱层参数如表3所示。

表3 棱柱层参数
网格数量对计算结果影响较大,有必要验证网格无关性。下压力作为本文中主要监测数值,其准确性至关重要。网格独立性验证如表4所示,复杂流动区和尾迹区对结果有重要影响,因此设置2个网格加密区,其一对前翼、扩散器和尾翼加密,其二对赛车尾流加密。从表4可以看出,随着体网格数增加,下压力急剧下降,当网格数达到2 000万后,下压力略有变化。因此,考虑到计算效率,确定流动复杂区和尾迹区网格尺寸分别为8 mm和16 mm,总网格数量控制在2 000万~3 000万。
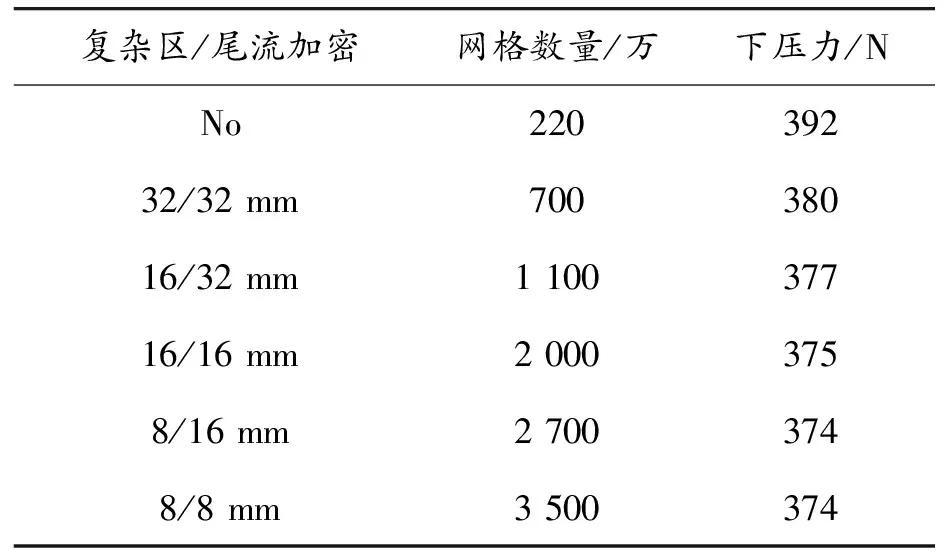
表4 网格独立性验证
具体体网格数如表5所示。由于运动轨迹不同,直线和弯道背景域存在一定差异。2种工况重叠域网格数均保持在2 000万左右。
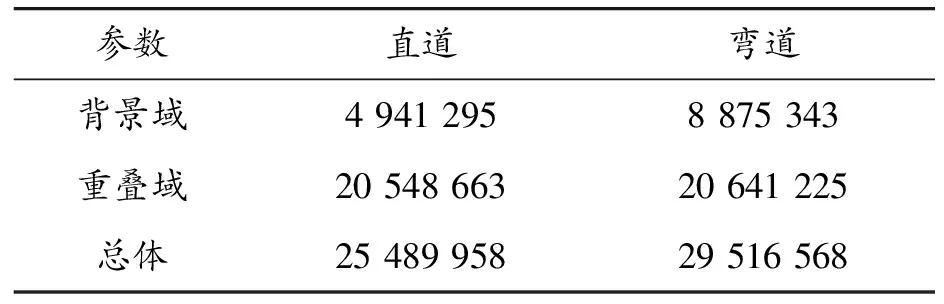
表5 体网格数
1.5 湍流模型
本研究主要应用Reynold-averaged Navier-Stokes(RANS)进行数值模拟,目前得到普遍应用[22-24]。RANS湍流模型包括Realizablek-ε、Standardk-ε、SSTk-ω等。SSTk-ω湍流模型被证明是一种能较好地预测赛车下压力的模型[25],并被广泛应用[26-27]。SSTk-ω结合了k-ω模型在壁面附近的准确性和k-ε在自由流中的鲁棒性,其考虑了湍流剪应力的传输,可以很好地预测逆压梯度下的流动起始和分离量[28]。
2 结果与分析
2.1 气动力结果
图7为总气动力结果。从图7可以看出,与直道相比,FSAE赛车在弯道中总气动力出现较明显变化。弯道工况下阻力和下压力有不同程度的增加,气动阻力为188.2 N,与直道相比增加1.5%,下压力为399.2 N,增加6.5%。表明,弯道工况中下压力比阻力更敏感。
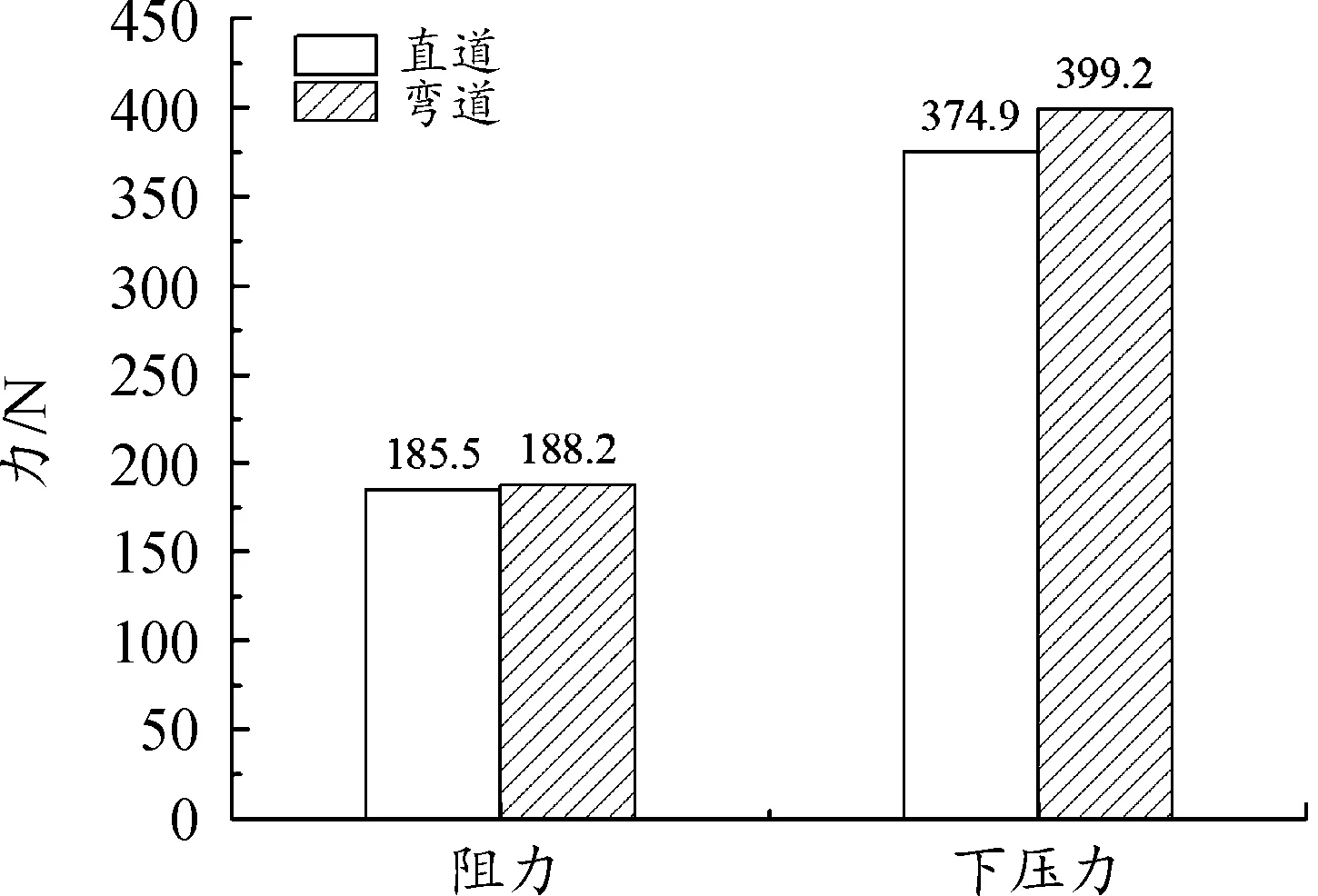
图7 总气动力结果
图8为各部件的气动力结果。图8(a)为下压力变化,除前翼外,其余部件在弯道时下压力均有不同幅度地增加,增幅主要来自扩散器和车身,分别增加11%和18.3%,尾翼下压力增加2.5%,前翼下压力减少约3%。图8(b)显示各部件气动阻力变化,变化最大的为前翼阻力的增加,与直道相比增加约14.8%。扩散器和车身阻力分别增加约11%和2.6%,尾翼和车轮阻力分别减少约1%和7.4%。下压力变化对弯道中赛车的性能影响更大。
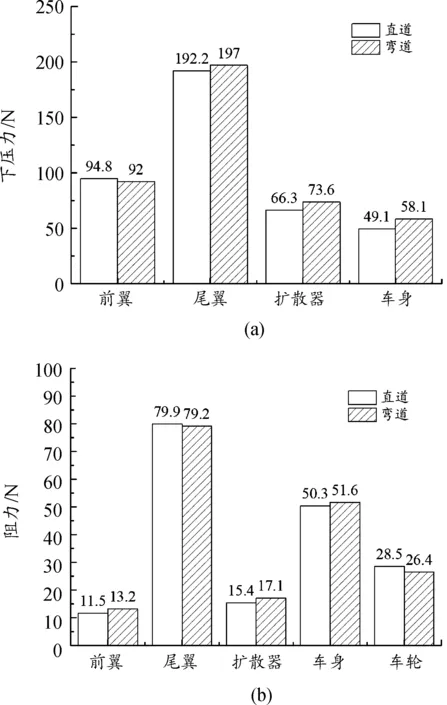
图8 各部件气动力结果
2.2 气动力矩结果
除了气动力外,气动力矩对赛车操纵稳定性有较大影响[29]。气动载荷变化与总气动力矩如表6所示,%F表示前轴气动载荷与总气动载荷之比,Mx和Mz分别为气动侧倾力矩和横摆力矩。气动力矩均以图6所示坐标系为基准,弯道工况下%F为30.8%,与直道相比下降1.1%,弯道工况下Mx和Mz分别为-13.5 N·m和-43.1 N·m。
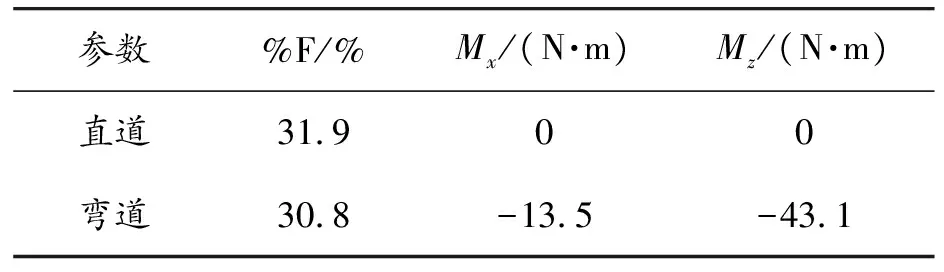
表6 弯道中气动力矩的变化
为直观理解气动力矩对操纵稳定性的影响,弯道工况中气动力矩如图9所示,%F的降低会减少前轴载荷与前轮抓地力,增加弯道中的转向不足趋势。负侧倾力矩会减小赛车车身左右两侧的气动载荷之差。负横摆力矩会抑制赛车在弯道中的入弯趋势,进而导致转向不足。综合以上分析,弯中产生的气动力矩会增加赛车的转向不足,导致赛车在过弯时转向更为迟钝,对整车操纵稳定性较为不利。

图9 弯道工况中气动力矩的影响
2.3 流场分析
根据上述直道和弯道工况中气动力和力矩值,两截面的速度场分布对比如图10所示,速度参考系选取为运动中的赛车。本文中主要关注前翼与尾翼端板附近流场,因此,在纵向上创建了Z=-200 mm和Z=700 mm的截面,如图10(c)所示。图10(a)为Z=-200 mm处的速度分布对比,如箭头所示,前翼端板在弯道外侧有扰乱高速气流现象,同时前轮尾迹存在不同,在弯道外侧有更多低速区。图10(b)为Z=700 mm的速度分布对比。从图中可观察到尾翼附近流场,尾翼后方有一个速度较低的尾流区域(如图中虚线所示),弯道工况下尾流区域与直道相比有明显的气流扭转现象。如箭头所示,尾翼前端内侧端板出现气流分离现象。
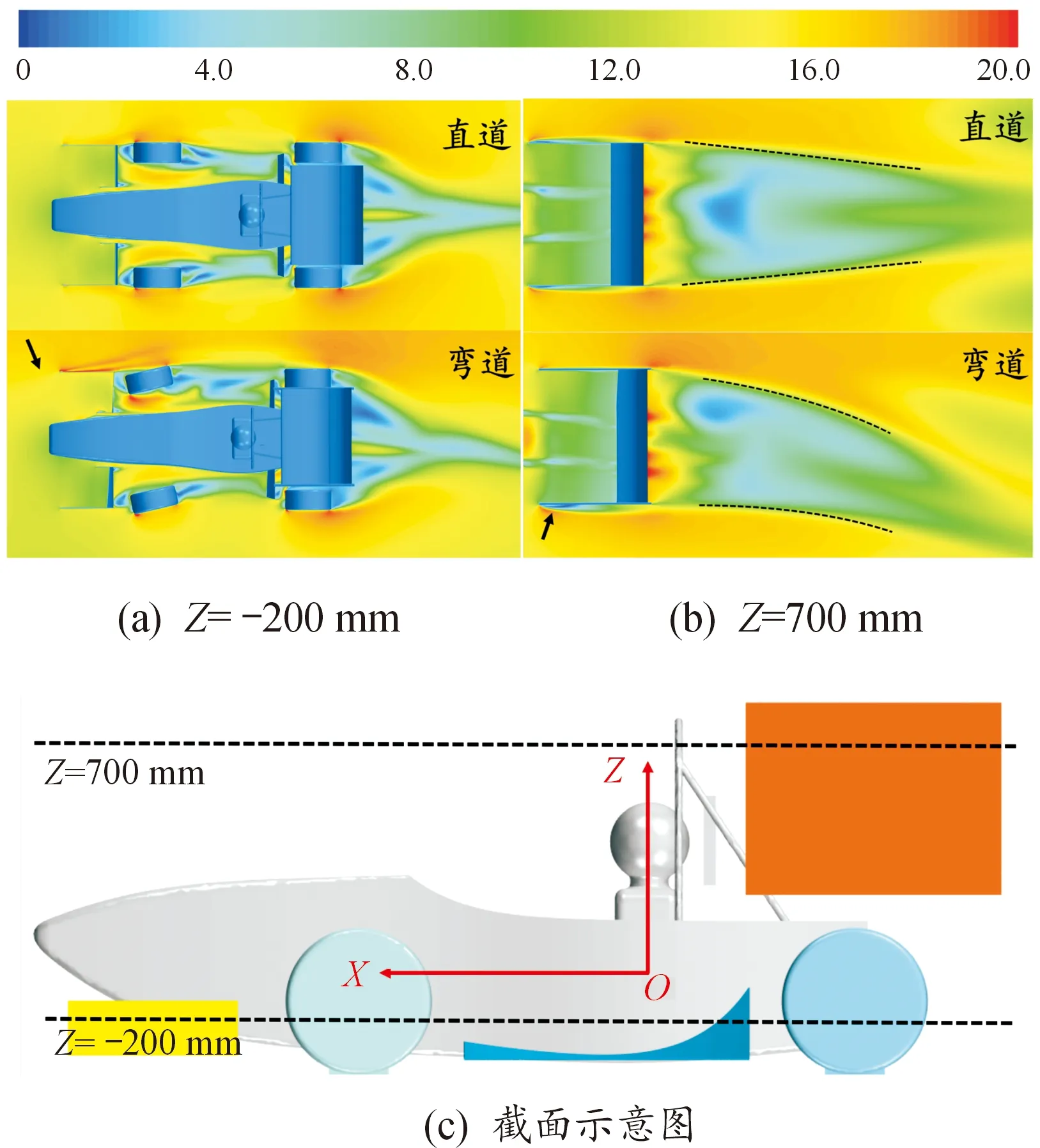
图10 速度分布对比
压力系数分布如图11所示。图11(a)为上表面,从中心轴左右对比来看,弯道中表面压力呈现较大不对称分布,如箭头所示,大部分正压力积聚在翼片的弯道外部一侧(包括前翼和后翼),这会造成一定的侧倾力矩,加大左右两侧气动载荷分布。底板表面压力分布如图11(b)所示,与正压分布相比,负压分布不对称趋势更强。图中箭头所示,较多的负压分布在弯道外侧,包括前翼和扩散器,原因其一为外部气流流速较快,其二为弯道外侧车身侧倾角导致离地间隙减小,增加了扩散器地面效应。
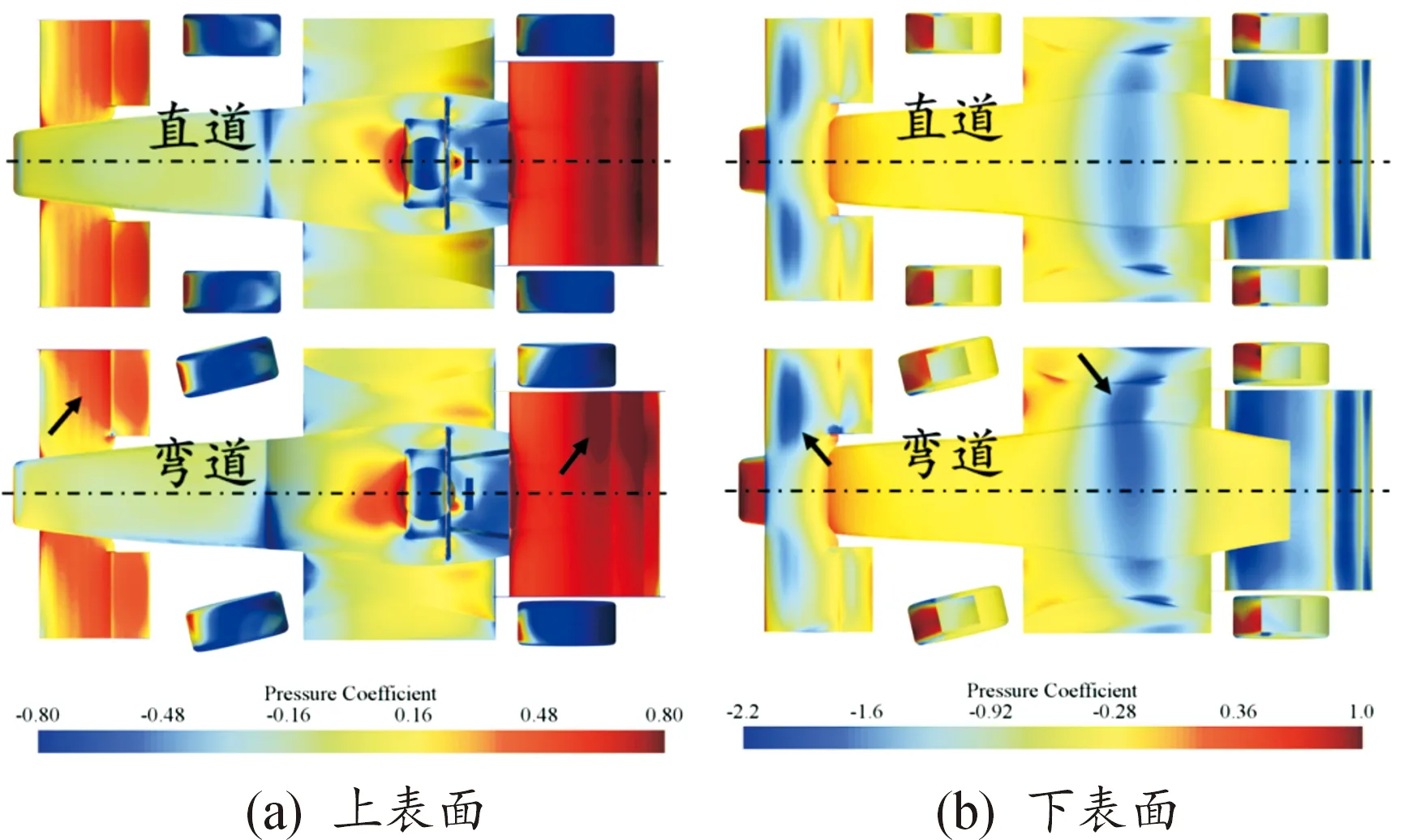
图11 压力系数分布
为验证侧倾角引起底板负压分布变化这一假设,对无侧倾角工况进行模拟,结果如图12所示。侧倾角存在对底板负压分布有重要影响,有侧倾角下底板负压较大,产生了更多下压力,因此侧倾角存在是引起弯道中扩散器和底板下压力增加的主要原因。
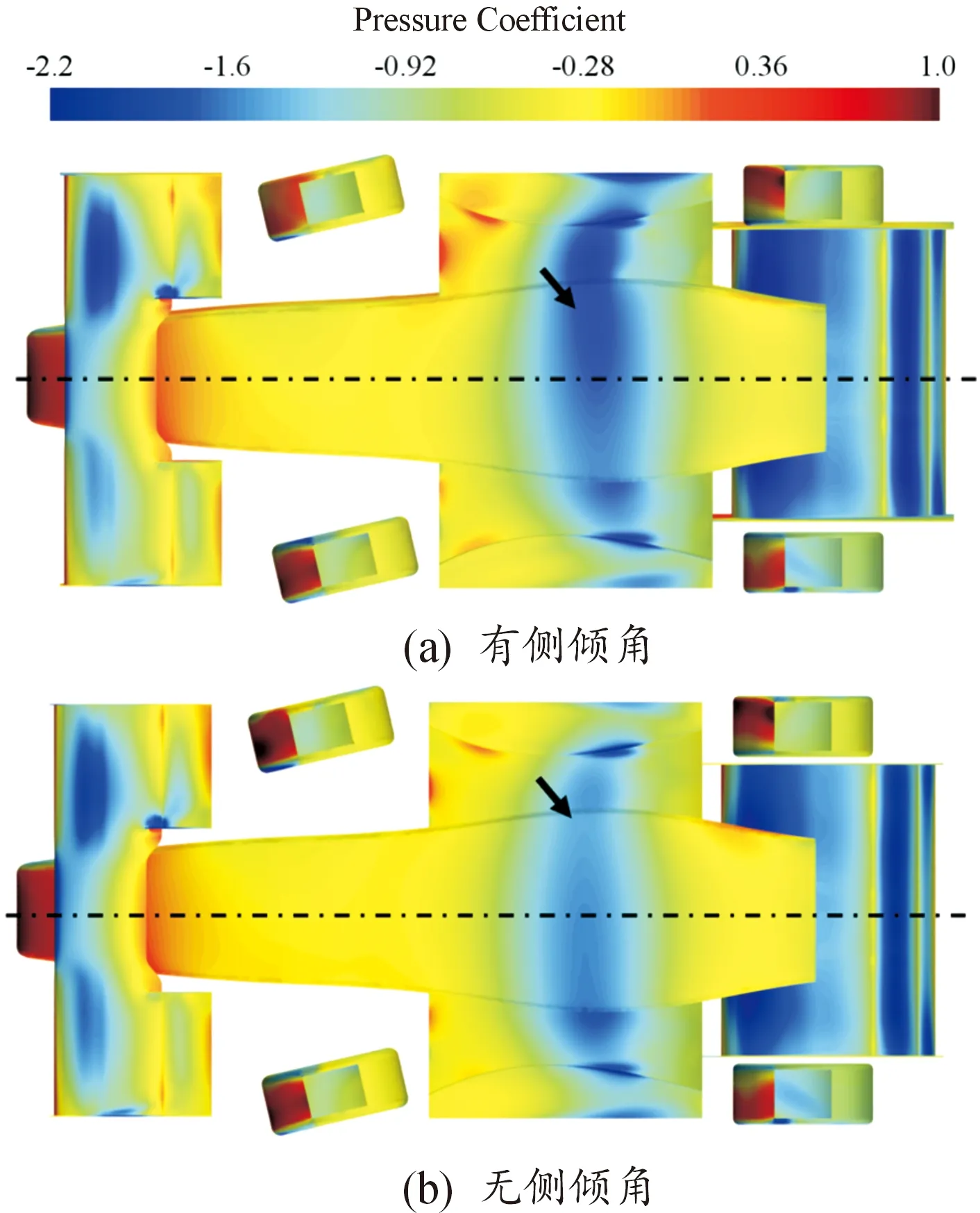
图12 有无侧倾角底板表面压力对比
本研究采用Q准则来识别涡结构以及捕捉涡轨迹。Hunt等提出将Q>0的区域定义为漩涡[30],这意味着在涡区域内,流体旋转涡量大于变形涡量。Q准则是一个基于速度梯度张量的特征向量和特征函数,需要设定阈值来显示涡旋结构。
图13是FSAE赛车主要涡结构变化,Q值选择为5 000 s-2以筛选出明显涡结构。如图13(a)所示,在直道工况中前翼两侧产生一对翼尖涡,命名为FW-TV(front wing-tip vortex),尾翼产生的一对翼尖涡命名为RW-TV(rear wing-tip vortex)。图13(b)显示弯道工况下涡的运动轨迹,其涡名称尾部字母L和R分别代表车身左右侧涡,同时也代表弯道内外侧的涡。在直线工况下,左右两侧涡的形态和轨迹均呈对称分布,且FW-TV和RW-TV具有较长的纵向尾迹。弯道中2对涡轨迹沿一定曲率向下游发展,车身左右两侧涡对的发展和轨迹呈不对称分布,位于弯道内侧的FW-TV-L涡与具有转角的左前轮撞击而破碎,阻止了其向下游运动,这是导致前翼下压力损失的主要原因。位于弯道外侧的FW-TV-R涡尾迹区相比于直道更长,这是由于来流的曲率影响使FW-TV-R涡沿车身外侧流动,对于弯道工况中的RW-TV涡,则体现出不同趋势,位于弯道内侧的RW-TV-L涡纵向尾涡尾迹区比弯道外侧RW-TV-R的长,这种差异体现出弯道内外侧不同的流动特性。
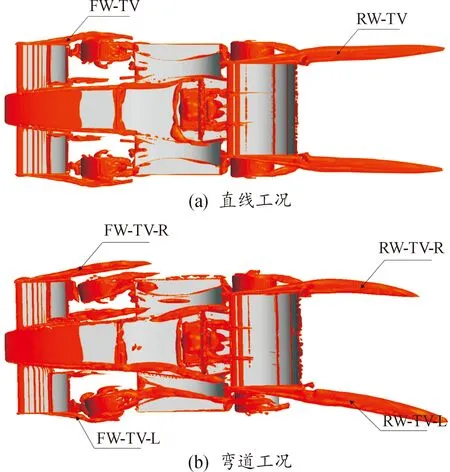
图13 整车主要涡结构变化
3 八字绕环试验
八字绕环(skid pad)是一种特殊的弯道工况,它可以测试FSAE赛车的操稳性。以2021赛季重庆理工大学FSCC赛车为基础,分别进行模拟仿真和八字绕环试验。
3.1 CFD模拟
八字绕环(Skid Pad)是FSAE赛车动态赛事之一,旨在测试赛车在固定半径转弯时在平地上的转向能力。八字绕环布局如图14所示,两圆心之间的距离为18.25 m,内圆直径为15.25 m,外圆直径为21.25 m,赛道宽度为3 m,结合车宽,汽车质心的行驶半径约8.5 m。

图14 八字绕环布局
实验仿真模型如图15所示,实验模型采用21赛季重庆理工大学Thimchi 39赛车,实车模型如图15(a)所示。为验证八字绕环实验,需建立与试验模型相对应的仿真模型,如图15(b)所示,该模型保留了实车大部分特征,对翼片和扩散器进行精细化处理,简化了轮胎、发动机和减震器,去掉外露的软管、螺栓等小部件。

图15 试验所用模型
为保证与八字绕环试验条件一致,在数值模拟中,转向半径8.5 m,在八字绕环中环绕一圈时间为6 s。其余边界条件保持相同。
仿真结果如图16所示,包括气动力和力矩。图16(a)为总气动力,总气动阻力与下压力分别为77.3 N和123.9 N,各部件气动阻力和下压力分别如图16(b)和图16(c)所示,气动力矩如图16(d)所示,FSAE赛车在八字绕环时会产生负气动力矩。气动力与气动力矩变化趋势与简化FSAE模型相同,验证了本研究的普适性。

图16 仿真结果
3.2 试验过程
安装在车身上的线位移传感器用于测量总下压力。线位移传感器的安装位置如图17所示,如图中箭头所示,线位移传感器安装在每个减振器两端,并伴随减振器做相同反弹和压缩运动。在弹簧线性刚度条件下,通过测量减振器变化量来计算整车下压力。

图17 线位移传感器的安装位置
试验地点在重庆大足汽车试验场,如图18所示。试验场的平整路面减少了惯性力对结果影响,使用桩桶铺设八字绕环赛道,绕行一圈时间控制在6 s左右,车手尽量保持匀速绕桩。

图18 重庆大足试验场
实验数据处理过程如图19所示,图19(a)为数据采集的过程,线位移传感器将采集的数据转换为电压信号并存储在电子控制单元(ECU)中,用外部电脑提取存储的数据,对数据进行处理,最后转换成下压力值。图19(b)为线位移传感器采集的初始数据,使用Motec软件读取ECU中数据,包括油门开度、制动踏板开度、方向盘转角、车速等随时间变化的数据。本试验主要关注位移变化如方框所示。如图19 (c)所示,从初始数据中提取0.5 s波动较小的数据,采样频率为500 Hz,因此一个传感器在此时间段内采集251个数据,随后对这段数据进行统计和处理,处理结果如图19(d)所示,FL、FR、RL和RR分别代表前左、前右、后左和后右减振器位移量。
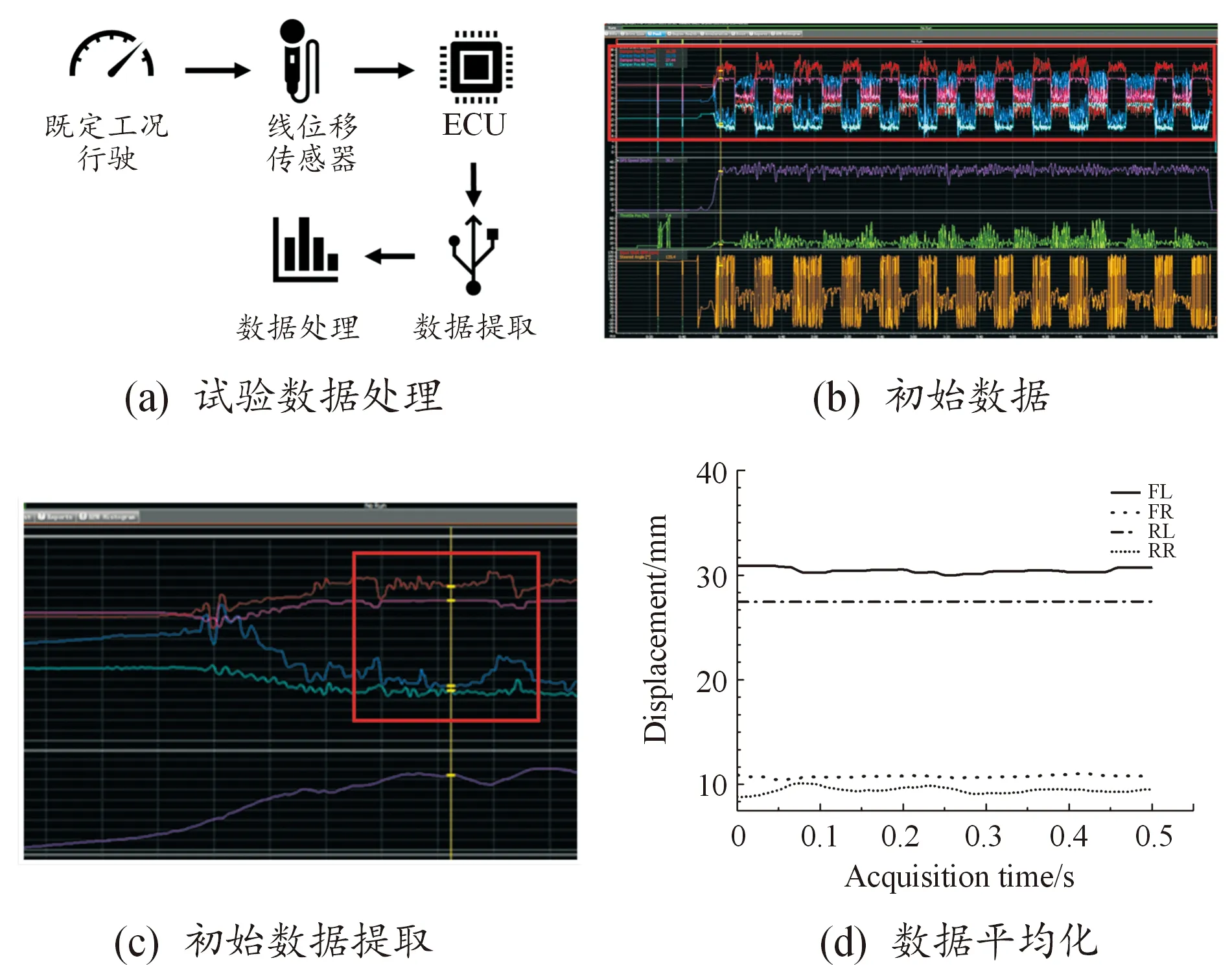
图19 数据处理过程
驾驶员坐入赛车静止不动时,将传感器采集到的数据作为静态数据,在既定工况驾驶后,对动态数据中0.5 s内取平均,如表7所示为数据统计,正值(+)表示减震器被拉伸,负值(-)表示减震器被压缩。
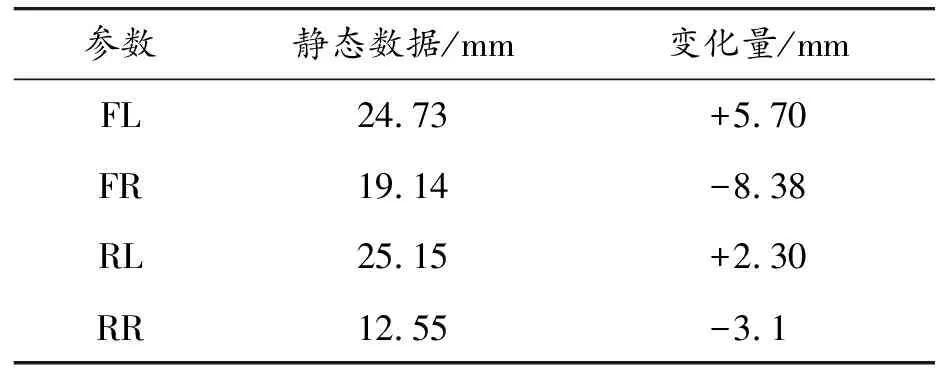
表7 数据统计
线位移数据变化如图20所示。图20(a)为各个减振器的变化。从图中可以看到弯道外侧减振器被压缩,弯道内侧减振器被拉伸。将两侧的数值加和为前后轴荷的变化,如图20(b)所示,前轴被压缩2.68 mm,后轴被压缩0.8 mm,这是由于存在的气动下压力导致车身压向路面,前后减振器弹簧均被压缩。

图20 线位移变化量可视化
根据胡克定律[31],减振器默认为线性弹簧,忽略第三弹簧与防倾杆刚度的影响,汽车前后减振器弹簧型号为200磅,根据刚度折算为30 250 N/m。
DFF=-0.002 68mm×35 025 N/m=-93.9 N
DFR=-0.000 8 mm×35 025 N/m=-28 N
DFTotal=DFF+DFR=-121.9 N
式中:DFF为前轴转换后的下压力;DFR为后轴的下压力。DFF和DFR的值不代表真实值,因为从压缩量来看,前轴的压缩量明显大于后轴,说明有载荷转移存在,但DFTotal没有变化。在八字绕环中,整车气动下压力为121.9 N。
3.3 结果对比
实验与仿真的下压力对比如图21所示,试验值为121.9 N,略低于仿真值,误差约1.6%,造成误差的原因之一是轮胎变形,实际充气轮胎会比仿真模型大,另一个原因是散热器处理,忽略了旋转冷却风扇的影响。
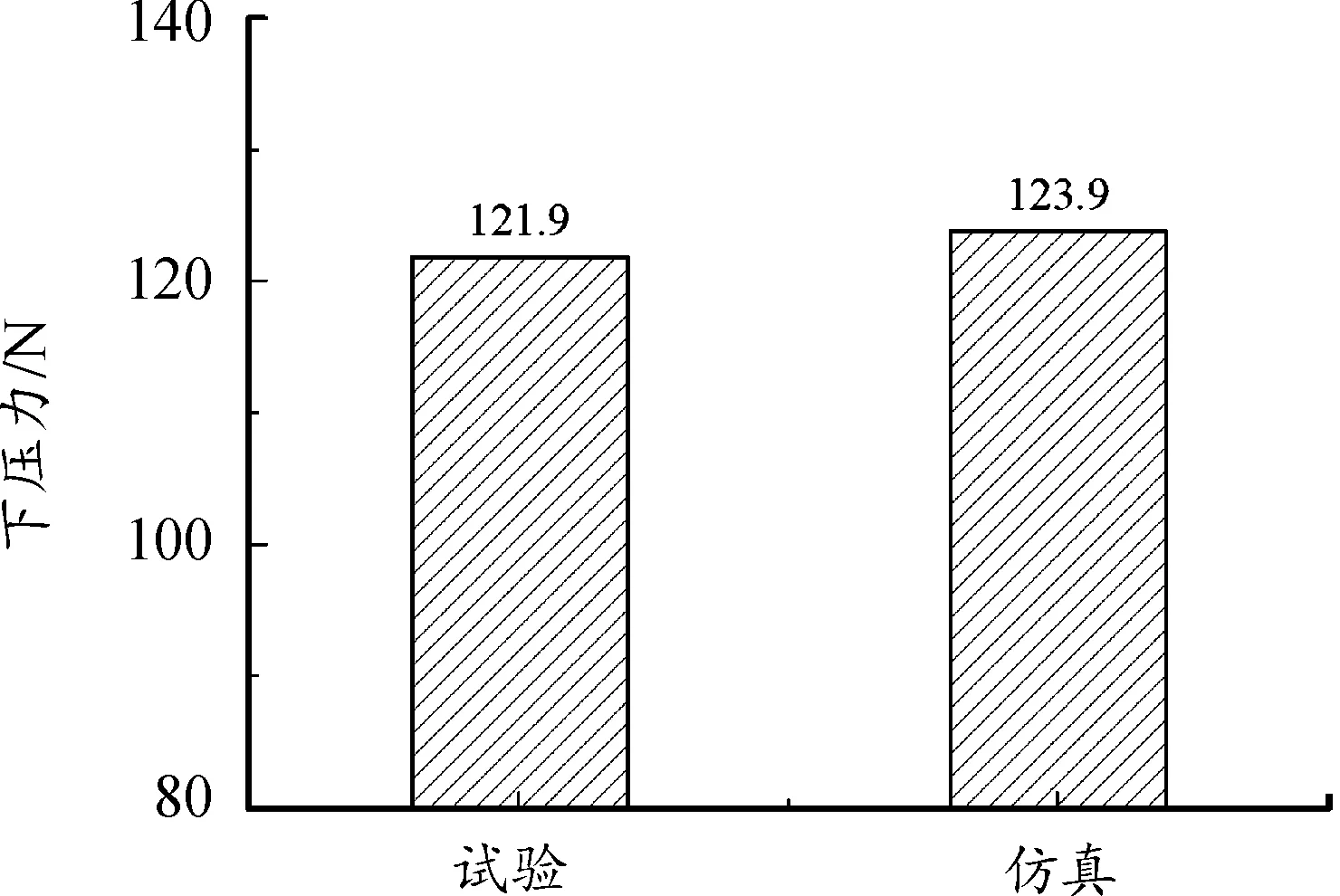
图21 试验与仿真下压力对比
试验验证了重叠网格方法模拟复杂工况的准确性。由于试验中可测量数据有限,需要更多仿真的数据,因此,CFD仿真结果可用于指导赛车设计和优化底盘调整。
4 结论
1) FSAE赛车在弯道中气动力发生较大变化,其中下压力增大6.5%,除前翼外,其他部件均有不同程度的增幅。下压力增加主要来自扩散器和底板。
2) 弯道中会产生额外气动力矩,俯仰力矩会使压力中心向后偏移,横摆力矩会降低FSAE赛车的转向灵敏度。由于气动力矩的存在,赛车会趋于转向不足,车手了解赛车气动力和力矩的变化,更好地驾驭赛车。
3) 弯道中车身表面静压分布高度不对称,尤其是底板处的负压,这是由于转弯时存在的侧倾角导致扩散器和车身下压力增大。
4) 涡结构在弯道中有较大变化,具有转角的前轮对弯道内侧前翼涡运动的阻滞效应是前翼下压力降低的主要原因,从涡轨迹可以看出,尾翼旋涡的轨迹发生了一定程度的偏转,尾翼端板气流在弯道中发生气流分离。
5) 利用线位移传感器监测和计算FSAE赛车在八字绕环中的气动下压力。结果表明,实测下压力值与数值模拟相差1.6%,吻合度较好。
在本研究中,有一些现象值得进一步研究。首先,倒置翼片是赛车中产生下压力的主要方式之一,在本研究中,弯道下翼片产生的下压力没有体现显著差异,因此需要进一步研究曲率流动下机翼的气动特性,如升阻性能、临界攻角变化、壁面附近边界层流动等。此外,如何减小曲率流动中端板的分离是后续研究的重点。
