交叉口下游公交站点对车辆饱和流率的影响

张东方

（长春市市政工程设计研究院有限责任公司，长春 130033）

引言

公交停靠站是公交车运行过程中的重要节点，分布在城市各处，是提供公交服务、满足乘客出行的基础设施。在城市道路中，直线式公交站点是最为常见的，同时直线式公交站点相较于港湾式公交站点对交通的影响更大，由于公交车辆停靠时会占用一条机动车道，导致路段通行能力折减，对交叉口的通行流率造成影响。为了降低公交站点对车辆通行的干扰，分析公交站点对交叉口车辆饱和流率的影响是有必要的。

当前学者对于公交站点设置及其影响的研究已经相当丰富。Bunker[1]使用概率方法对公交站点的选择和公交车堵塞进行建模，该模型量化了乘客在车站的等候时长，用来评估乘客的服务质量。Baeza 等[2]对公交停靠站给公交乘客及其他正常行驶车流造成的影响进行数据分析，并将相应数据进行了交通仿真，用各类型公交站点与人、车形成联系并相互作用，研究分析了公交停靠站的布局问题。Bowman 等[3]则建立基于乘客感受的等候时间敏感度模型，用于对这类情况下直线式公交站点通行能力、服务水平等因素的计算，并提出改善建议。吕小峰和周骞[4]以直线式公交站点为研究对象，考虑公交车到达、停靠时间和公交车到达时间重合排队的概率，建立多因素影响模型，得出公交停靠站泊位数最佳区间。朱丽南[5]运用交通经济学和资源经济理论研究北京市常规公交站点局部拥堵的影响，通过在传统路阻函数中加入公交车停靠的因素建立模型进行分析，得到直线式公交站点对路段通行速度的影响幅度。刘安[6]将返回波理论应用于公交停靠站对路段进口交叉口的影响上，以此分析了公交车辆进站和出站时产生的聚集和离散波，计算得出了公交停靠站的影响范围和适宜交通流的位置。

目前，国内外对于公交车停靠影响的研究已经有许多成果，但多数研究是以实地观测的实际数据对各类因素进行拟合标定，这种方法得出的模型与结论虽然对实际调查的道路具有很好的实用性，但是仅适于特定的调查路段，普遍性适用性较差。本文在阅读国内外有关公交站点影响及道路饱和流率研究的文献基础上，对有无公交车停靠影响下的交通流进行传输分析，对公交车在直线式公交站点停靠过程进行分析，寻找公交车停靠对周围车辆产生影响的因素，根据合并折减系数和车流率特点对所建模型进行数值分析，得到公交车在交叉口下游停靠对道路和交叉口饱和流率的折减幅度，为公交站点设计布局和交叉口信号配时影响因素提供参考依据。

1 问题描述

公交车需要在指定站点停靠，如果公交站点设计不当，不仅不能缓解城市的交通压力，而且会使得公交站点成为路段拥堵的源头。对靠近交叉口的直线式公交站点，公交车停靠时会影响道路上其他车辆的正常行驶，进而影响交叉口的通行效率，造成交叉口堵塞。因此，本文为了减少公交站点的布设对其他车辆通行的影响，在不考虑对向车流、非机动车以及行人影响的情况下，当公交车离散到达时，借助元胞自动机模型研究分析交叉口下游公交站点的布设对车辆饱和流率的影响。

2 交叉口下游直线式站点影响模型建立

2.1 公交到达情况分析

对于下游直线式公交停靠站，根据红绿灯变化、排队阻塞和公交车到达等因素，可以分为以下四种情况。

2.1.1 公交车没有到达站点且交叉口为绿灯

这种情况下，可以看作交通流在路段上以自由流车速正常行驶的状态到达并通过交叉口，每个元胞内的车流在下一秒都能到达下个元胞。为了使公式更具有适用性，设置采样间隔时间为k，则单个元胞在下一个采样时刻满足如下关系式：

式中，ni(t)为第i个元胞第t时刻容纳的车辆数；vf为车辆自由流速度；r为车道数目；ρi为第i个元胞当前的单车道密度；fi(t)为其他元胞的输入流量；k为采样间隔时间。

2.1.2 公交车到达站点停靠且交叉口为绿灯

这种情况下，公交车随着绿灯释放的车流前进，直到到达站点停靠。随着交叉口绿灯释放的流量变化及公交车到达站点的时间节点，公交车停靠时满足如下关系式：

式中，fg(t)为公交车停靠站后一个元胞的输入量；γx为下游公交站点合并系数，取值范围0 ＜γx≤1；ρj为阻塞密度；qmax为路段实际能达到的最大通行能力；w为交通拥挤时车流波的反向传播速度（w＜vf）。

2.1.3 公交车在绿灯末期到达并在停靠且交叉口为红灯

这种情况下，公交车还在停靠而交叉口处不再释放车流，此时公交车辆的停靠不影响交叉口的流率。当公交车开始离站时，如果公交车后续还有车辆，将随着公交车一同驶离，满足式（3）；若公交车离开时后续已无车流，则公交车独自离开，满足式（4）。

式中，fj(t)为从进口道到交叉口第一个元胞的输入流量；fg(t)为公交车停靠站后一个元胞的输入量；g代表t时刻最后一个元胞，ρg为最后一个元胞当前的单车道密度；Nt代表t时刻第g-1 个元胞容纳的车辆数。

2.1.4 交叉口为红灯没有公交车停靠

这种情况下，交叉口为红灯，红灯时期交叉口出口道没有车流流动，也就没有公交到达的情况，满足式（5）。

2.2 饱和流率折减幅度

结合元胞传输模型的传输特点对交叉口饱和流率进行识别，当红灯变绿灯交通流开始释放时，需要读取相应数值并记录持续时间直到绿灯结束，将符合要求的流量和所用时间累加，最后用式（6）计算得到某一因素变化下，受公交车影响的饱和流率在无公交车影响下饱和流率的折减幅度zf。

3 数值分析

3.1 设计实验

通过分析公交车的到达情况，将公交车的不同到达情况运用元胞自动机模型表现出来，运用MATLAB 语言搭建仿真平台，以饱和流率折减幅度为评价指标，设计实验并探究交叉口下游公交站点对车辆饱和流率的影响。

设计单向双车道次干路，路幅为四幅路，站点类型为近端直线式公交停靠站，沿机非分隔带设置，自由流速度50km/h，阻塞密度为180 辆/km·lane，单车道通行能力为1500 辆/h·lane。设定最初交叉口信号配时为绿灯50s 红灯70s 的两相位，停靠时间20s，上游输入流率400 辆/h·lane，车流合并折减系数为0.5，采样时间间隔取1s。交叉口下游直线式公交站点与交叉口距离为2 个元胞大小（约28m）。

合并折减系数是指当公交车停靠挡住一条车道时，后续车流陆续合并到其他车道上，由于车辆合流会互相影响造成车辆延误，降低实际的通行效率，因此根据原先交通流密度的大小，对通过元胞传输模型运行得到的通行流量进行一定的折减。为了突显公交车停靠的影响，若公交车停靠后能够通行车辆的车道满足上游输入流率的通行需求，则合并折减系数取0.5 左右。如果不能满足需求则说明流率较大，合并折减系数可以取1。

合并折减系数、站点与交叉口的距离对车辆饱和流率影响较大，因此以上游流率、合并折减系数、站点与交叉口的距离为输入变量，以受公交车停靠影响的饱和流率占不受影响的交叉口饱和流率之比率（饱和流率折减幅度）为因变量，研究直线式公交站点对交叉口饱和流率的影响。

3.2 数值分析

根据上述设计实验，采用控制变量法对车道合并折减系数和车辆到达率进行灵敏性分析。

3.2.1 合并折减系数影响

在控制其他变量按照最初设定的情况下，对公交车停靠处两车道车流合并从一个车道驶出的折减系数进行改变，折减系数由0.6 依次增加0.05 到1，运行程序计算结果如图1 所示。

图1 中横坐标为合并折减系数，纵坐标为受公交车影响的饱和流率折减幅度。当合并折减系数变小时，交叉口受公交车停靠影响的饱和流率折减幅度变大。

3.2.2 输入流率影响

在控制其他变量按照最初设定的情况下，对输入流率进行改变，从300 辆/h 到500 辆/h 依次以50 辆/h 递增，运行程序并按照车辆到达时的不同流率情况计算，其结果如图2 所示。

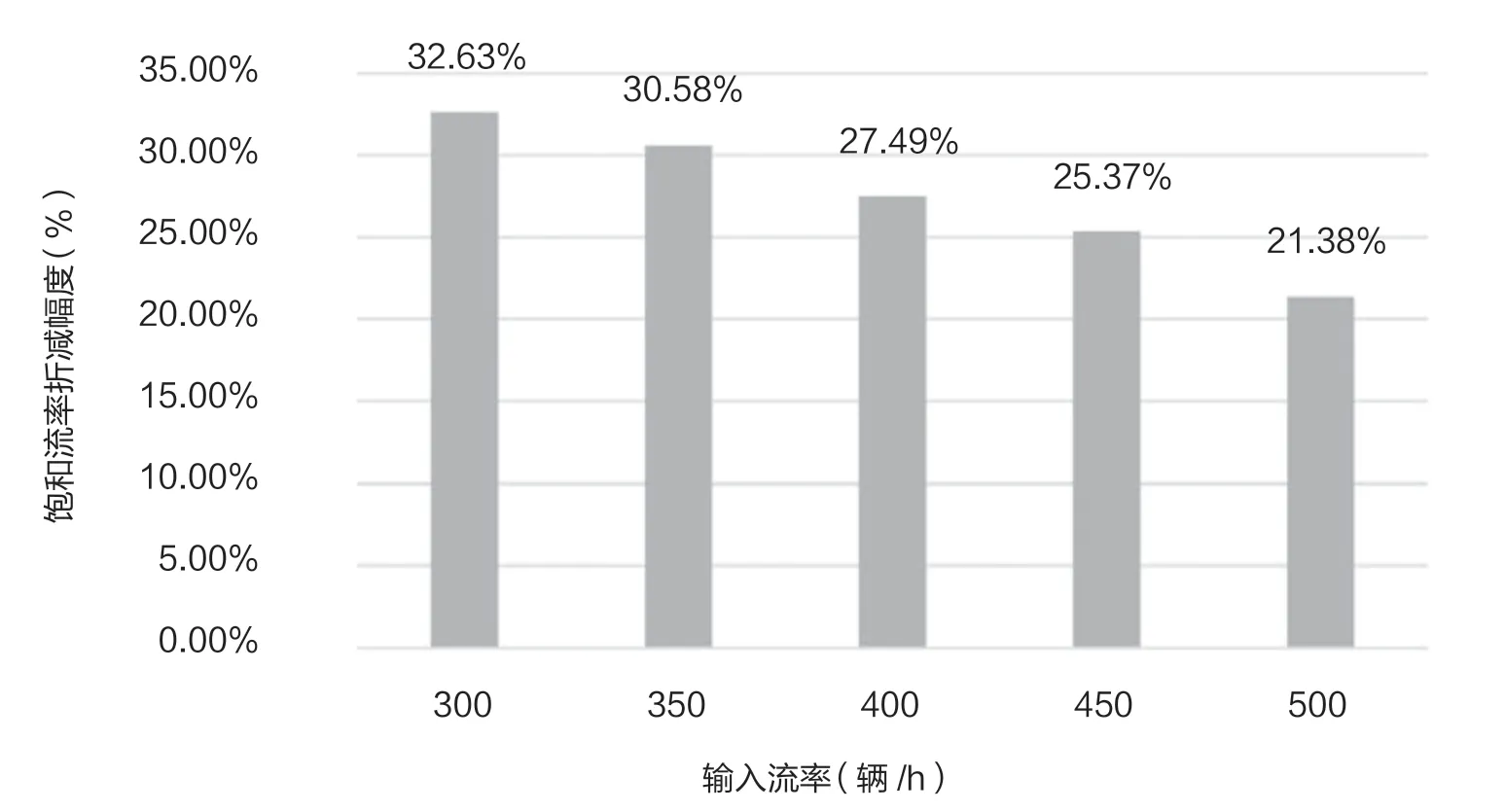
图2 下游流率变化下饱和流率折减幅度

图2 中横坐标为路段输入流率，纵坐标为受公交车影响的饱和流率折减幅度。当下游输入流率增大时，交叉口受公交车停靠影响的饱和流率折减幅度变小。从300 辆/h 到500 辆/h 的流率变化中，折减幅度降低了10%左右，可以看出，输入流率对交叉口下游直线式公交站点影响下交叉口饱和流率的影响幅度较大。

4 结语

本文通过元胞自动机模型研究交叉口下游直线式公交站点对交叉口饱和流率的影响，分析公交车到达交叉口时的不同情况，建立交叉口下游公交站点对饱和流率的影响模型。

经实验验证，在交叉口下游设立公交站点降低了交叉口的饱和流率，而且饱和流率折减幅度随着车道合并系数和车流率的增加而减少。