预应力陶瓷组合结构的抗侵彻性能研究

马 昊,陈美多,苗春贺,王鹏飞,徐松林,2

(1.中国科学技术大学 中国科学院材料力学行为和设计重点实验室,合肥 230027;2.中国地震局地震预测研究所 高压物理与地震科技联合实验室,北京 100036)

陶瓷复合防护结构一般是以陶瓷为面板、以复合材料为背板胶粘而成的多层复合结构。对于复合装甲,陶瓷强度的提升对增强结构抗冲击性能具有决定性作用。陶瓷是一种高硬度、高抗压性、低密度的脆性材料,能够在各种极端温度下工作,在工程结构的应用中备受关注[1-2]。近年来越来越多地应用于装甲防护领域。但是,陶瓷性能的提升带来脆性的增加不利于运动中的防护结构[3];同时金属材料的性能目前已经应用得非常充分,很难带来显著的提升。为了实现现代轻量化和高韧性的要求,需要优化复合结构来提高抗侵彻过程中的能量耗散效率。由于目前陶瓷材料和复合材料的抗冲击性能已经接近极限,因此采用新观念设计出新的防护结构来提高抗侵彻能力就显得尤为重要。

国内外学者在陶瓷材料抗侵彻性能的提升方面已开展大量的研究工作,取得了显著的效果。邹慧辉等[4]研究了陶瓷-活性粉末混凝土的抗侵彻性能,为陶瓷材料在重要防护工程的推广使用提供参考。毛亮等[5]研究了钨合金球形破片侵彻陶瓷/DFRP(dyneema fiber reinforced plywood)复合靶的弹道极限速度。殷文骏等[6]针对平头弹高速撞击陶瓷复合靶板问题,改进了理论模型。对于双层的陶瓷复合装甲,Zhang等[7]提出了一种双层结构的解析设计方法,研究了双层陶瓷装甲防护效率的优化。Krishnan等[8]研究了具有完美材料模型的陶瓷复合装甲有限元模型。Feli等[9]提出了一种新的陶瓷复合装甲的弹孔数值模拟方法。在双层复合装甲的基础上,Guo等[10]研究了Kevlar-29复合材料覆盖层对双层装甲的影响,Xin等[11]研究了玻璃覆盖层对透明陶瓷装甲弹道性能的影响。Hu等[12]研究了一种抗平头弹冲击的多层复合装甲,Wang等[13]对多层复合材料装甲的设计与特性进行了研究。在复合结构抗冲击性能的设计和分析方面取得了较系统的成果。为进一步提高复合结构的抗冲击性能,近年来,研究人员提出采用预应力结构来提高材料强度,以更好地提高结构抗冲击性能。Holmquist等[14]研究了预应力陶瓷模型以及设计薄厚两种陶瓷靶板配置来了解预应力对于弹道冲击性能的影响。吴雪等[15]基于LS-DYNA软件模拟了预应力对于陶瓷材料抗侵彻性能的影响。Serjouei等[16-17]在试验和仿真两方面研究了预应力强度对双层陶瓷复合装甲的弹道冲击性能的影响。研究结果表明：在预应力的作用下,陶瓷结构的抗侵彻性能得到了很好的改善。但是,这些研究中的预应力是由于结构挤压而被动激发出来的,预应力值并不确定。

基于此,本文应用弹簧在复合结构内部对陶瓷施加已知的预应力,由弹簧、陶瓷,以及金属边框组合形成防护基元,将防护基元组合成预应力陶瓷组合结构。然后基于量纲分析方法确定该结构在高速冲击下的残余速度表达式,应用有限元数值分析方法分析了该预应力陶瓷组合结构的抗侵彻性能。

1 数值仿真模型

1.1 数值模型

新型预应力陶瓷组合结构主要是由组元板面和背板组成。其中,组元板面由多个正六边形结构组元构成。图1所示为单个组元的构成示意图,从外到内依次为：金属边框、弹簧和陶瓷片;背板是一个实心的金属板面,两者在一起构成了本文所要研究的预应力组合结构。

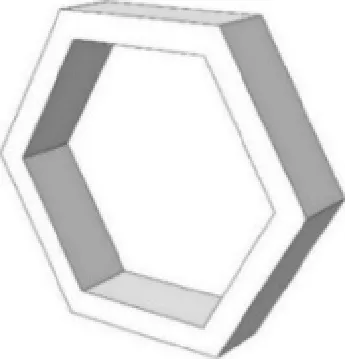
(a) 金属边框

利用ABAQUS有限元仿真软件建立防护结构计算模型。为简化问题,侵彻过程的子弹采用平头弹,直径为12.7 mm,弹长为20 mm。组元板面由19个组元结构构成,每个组元中陶瓷片边长为2 mm,弹簧长度为3 mm,金属边框的上下宽度为2 mm;组元板面和金属背板的厚度均为3 mm。模型装配图如图2所示。

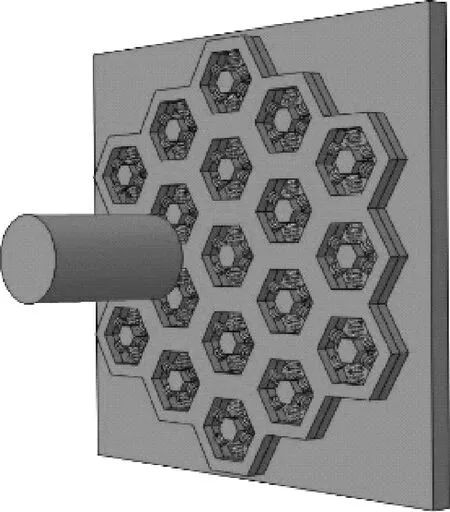
(a) 3维视图

1.2 材料参数

子弹材料为Q235钢,其参数为：密度7 850 kg/m3,弹性模量E=210 GPa,泊松比ν=0.3。背板材料为4340钢,其参数为：密度7 830 kg/m3,弹性模量E=200 GPa,泊松比ν=0.29。由于侵彻过程属于高速冲击过程,在整个过程中,材料会处于大变形、高应变率状态,材料的温度也会出现激增现象,而J-C(Johnson-Cook)本构模型能够很好地表征材料在冲击作用下的动态力学行为,特别是侵彻过程中材料的力学响应行为。因此,4340钢采用J-C本构模型和对应的动态破坏准则,该模型主要考虑了材料的应变强化效应、应变率效应和温度引起对的屈服效应。

J-C本构模型为

(1)

Johnson-Cook破坏准则为

(2)

式中：εf为等效破坏应变;D1～D5为材料常数值;σ*=σH/σeq为应力三轴度,σH为平均应力;其他参数与式(1)中含义相同。

4340钢J-C模型的本构参数和损伤参数的具体数值如表1所示。

表1 4340钢的J-C本构模型参数[18]

模型中的陶瓷材料为碳化硅(SiC)：密度为3 205 kg/m3,剪切模量为193 GPa,泊松比ν=0.14。硬脆陶瓷材料的仿真中JH-1和JH-2本构模型使用较多,本文采用的是JH-2模型。因为JH-2模型在JH-1模型的基础上考虑了材料强度的损伤劣化效应和材料梯度的破坏方程,可以实现脆性材料从不断累积塑性应变下的软化效应,对于侵彻过程中发生的大应变和高温、高压力情况,该本构模型能够更好的模拟陶瓷材料的力学响应行为。JH-2本构模型包括强度模型、损伤模型以及状态方程3个部分[19]。

强度模型为

σ=σi-D(σi-σf)

(3)

(4)

(5)

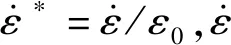
损伤模型为

(6)

(7)

压力模型

(8)

(9)

式中：K1为初始体积模量;K2,K3为体应变系数;μ为体应变,μ=ρ/ρ0-1,ρ和ρ0分别为材料当前密度和参考密度;β为能量转化系数;ΔU为弹性能的减少量。

SiC陶瓷的JH-2本构模型的参数详如表2所示。

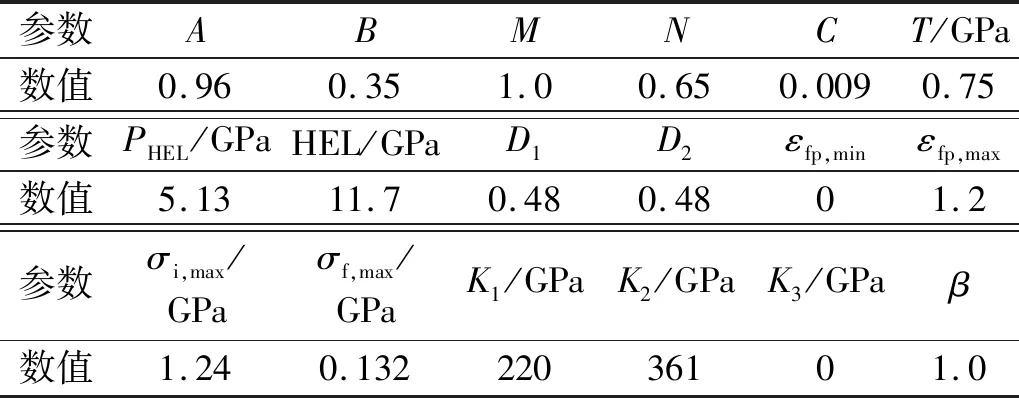
表2 SiC陶瓷JH-2本构模型参数[20]

1.3 预应力的施加

对于本文提出的新型组合防护结构,施加预应力的方式与传统的通过直接对目标施加位移进行压缩来产生预应力的方式有所不同。考虑到防护结构的特殊性,完成预应力的施加,首先要通过对单个弹簧施加位移约束,得到处于压缩状态的弹簧的应力数据。这里需要对结构中不同方位的弹簧都进行相同位移量的压缩,在ABAQUS软件中可以通过使用静力学分析步进行计算。得到相应的应力数据后,根据结构中的单元完成应力数据文件的写入,最后通过更改输入文件的关键字完成预应力的施加。

1.4 有限元计算结果的验证

陶瓷结构抗侵彻性能的数值分析很多,已有较为成熟的计算方法。本文进行的预应力陶瓷组合结构的数值仿真与已有的计算方法有不同之处,主要体现在预应力的施加过程中,本文主要是通过写入应力文件的方式在初始状态对结构赋予应力数值,不是通过直接位移压缩需要施加预应力的部件进行添加。为了保证结果的有效性,有必要对数值计算方法进行验证。为了验证所提出的有限元模型以及数值模拟方法的准确性,将有限元模拟结果与文献中已有的试验数据进行比较。参考Zhang等研究中陶瓷和铝合金组成的复合靶板的试验数据,使用文献中的材料参数进行数值模拟,得到的仿真数据与试验数据的对比结果如图3所示。

从图3的数据可以看出,在无预应力条件下,随着初始冲击速度的增加,子弹的残余速度也随之增加,根据图3仿真数据的曲线以及表3中的数据可知,仿真结果与试验数据的残余速度的差值不大,且误差均在合理范围之内。两者之间的一致性证明了有限元模型以及方法的可靠性。

表3 仿真数据与试验数据的对比

1.5 网格收敛性分析

为了保证结果的准确性,还需要对模型的网格进行收敛性分析。在该分析过程中,选取了5种不同的网格密度并统计其网格数量。对不同的网格数量模型进行相同初速度的子弹侵彻模拟,得到了参与速度结果如图4所示。从图4可知,当网格数量达到90 000后,继续增加网格密度对结果的影响很小,当前网格的精度已经满足计算要求。

图4 网格收敛性分析

2 量纲分析

首先需要分析预应力对侵彻过程的影响机制。以Mises屈服准则为例。在主应力空间,Mises准则可表示为

(10)

式中,K1为试验常数,也可以写为

(11)

如图5所示,预应力的施加使得材料的压缩屈服极限从零预应力时的A点变化到预应力为σ时的B点,其强度得到了提升。但是,由于冲击作用过程比较复杂,这种强度提升对材料侵彻性能的提高的相关性,需要进一步验证。

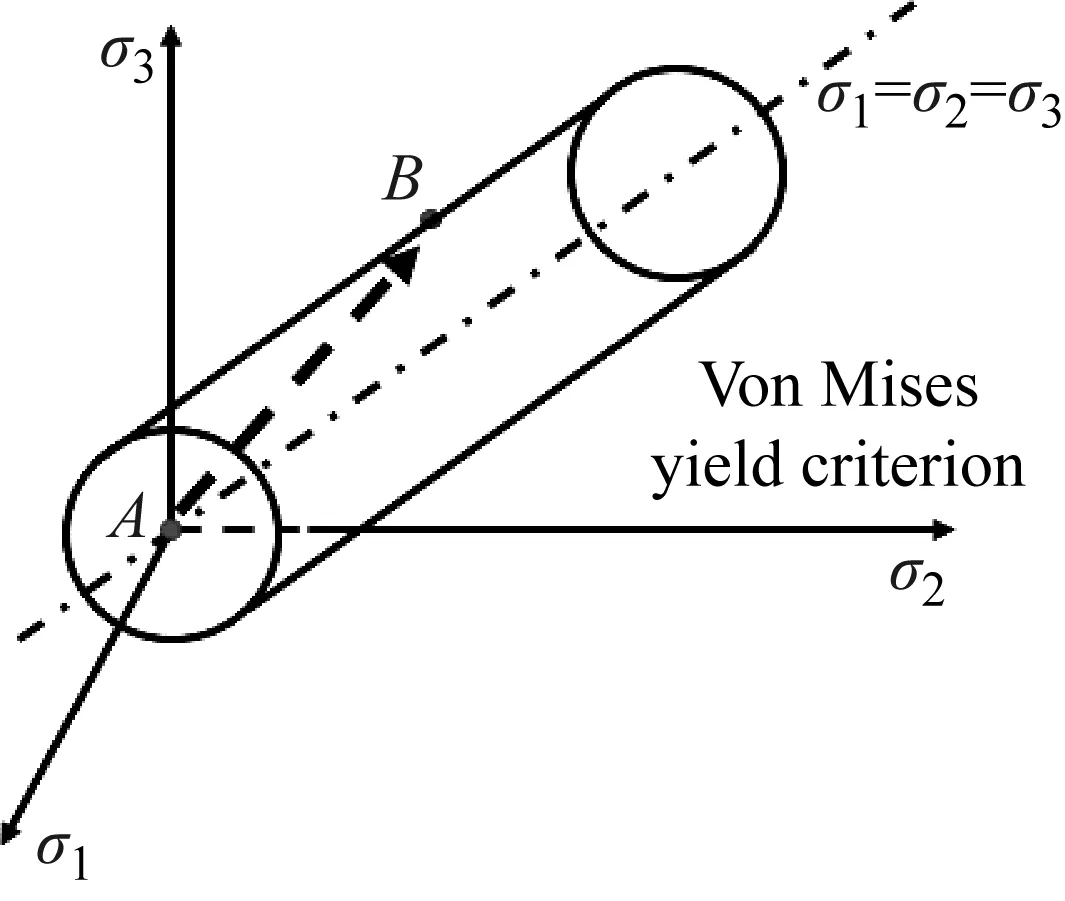
图5 强度变化

其次,此复合结构的量纲分析中选择残余速度作为分析对象。基于图1所示的几何结构和图2所示的数值分析模型,则残余速度可表达为

Vr=f(ρp,Ep,νp;Vp,Vc;ρt,Et,Yt,νt;σ,ε)

(12)

式中：ρp,Ep,νp,Vp,Vc分别为子弹的密度、弹性模量、泊松比、初始速度和残余速度;ρt,Et,Yt,νt分别为靶板的密度、弹性模量、屈服强度和泊松比;σ为弹簧施加的预应力;ε为靶板材料的断裂应变。

以ρt,Vc和Yt作为基本量,则式(12)的无量纲形式为

(13)

由于侵彻过程主要与惯性作用(密度ρ)、靶板强度(屈服强度Yt)、材料的压缩特性(Vp/Ct)以及结构中预应力的大小相关,因此侵彻过程的初步分析可集中于对这4个量的讨论。引入靶板材料的波速Ct,则无量纲残余速度的表达式为

(14)

将泊松比等其他材料参数代入,则可以得到残余速度的初步表达式为

(15)

式中,m1,m2,m3,m4为材料参数,可结合试验和数值分析综合确定。

3 预应力陶瓷组合结构的抗侵彻性能

3.1 预应力的影响规律

该节进行了5种不同速度下的平头弹侵彻过程的数值仿真计算,在每种速度下通过改变预应力大小来探究预应力对于组合结构的抗侵彻性能的影响规律。计算所得到的速度随时间变化的结果曲线部分如图6所示。图7为与图6相对应的速度下、不同预应力条件下,组元板在相同时刻的破坏程度对比图。由此可见：

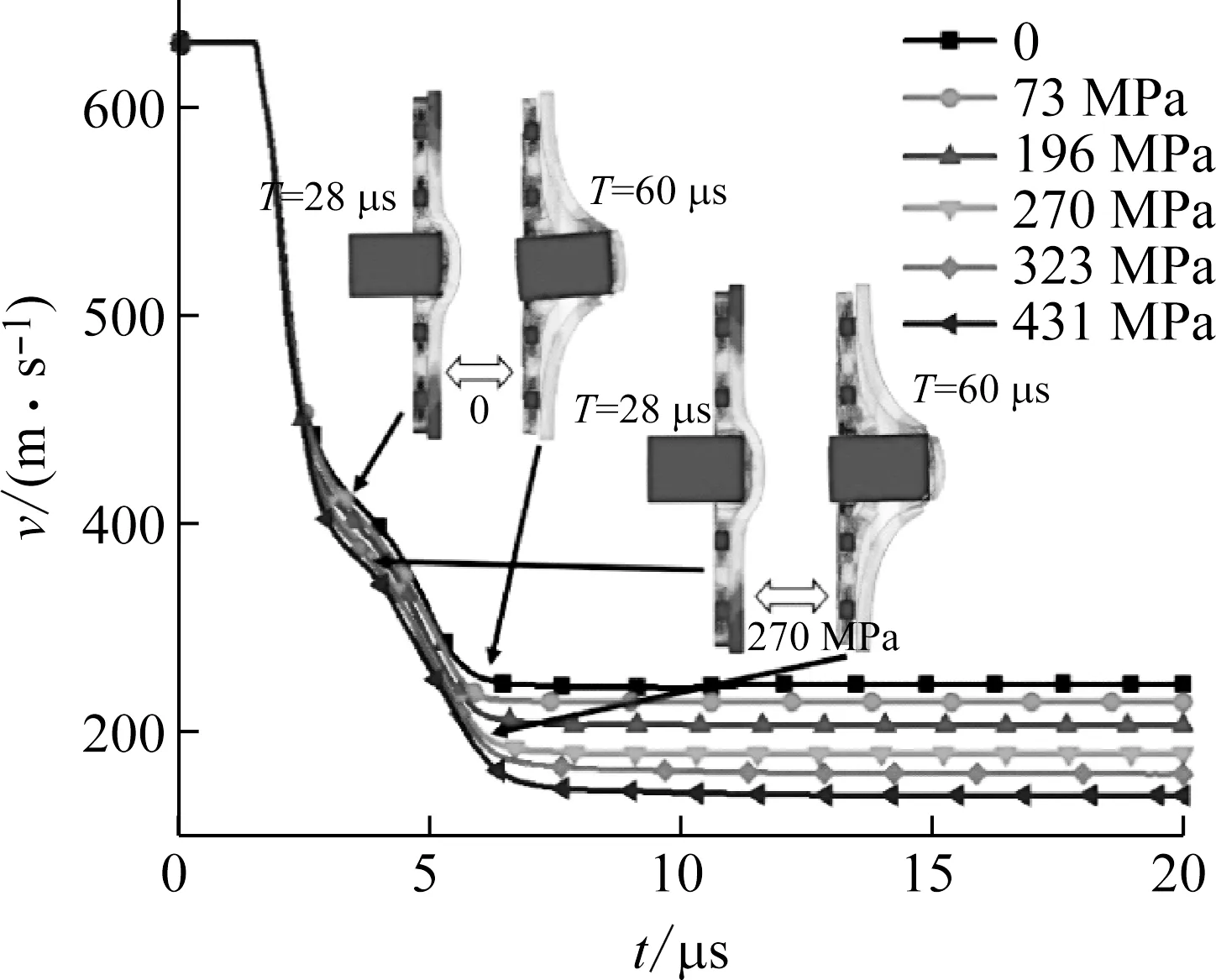
(a) 630 m/s

v=630 m/s,T=36 μs

(1) 图6表明在平头弹的侵彻过程中,子弹的速度从撞击时刻开始随着时间的增加逐渐减小,每条曲线都能够很明显的看到两个拐点,即对应着防护结构的双层板分别对子弹的抗侵彻过程;对比所得到的6条曲线,可以得知相对于无预应力条件,结构中弹簧施加的预应力能够增强组合结构的抗侵彻能力;而且随着结构中预应力的增大,子弹的侵彻残余速度逐渐减小,即结构的抗侵彻能力随着预应力的增加逐渐增强。

(2) 从图7的破坏形貌图可以直观地得到与无预应力情况相比,含有预应力的组元板面的破坏程度更小,说明预应力作用下结构对子弹的抗侵彻能力有着明显的增强;而且随着结构中预应力的增大,在相同时刻,组元板上受到平头弹冲击部分的破坏程度在逐渐减小,即因超过损伤失效位移值而删除的单元数量在逐渐减少,可以看出随着预应力增大,结构的抗侵彻能力也在逐渐增强。

以上结果说明在该结构中预应力能够很好的起到提高结构抗侵彻能力的作用。

3.2 面密度的影响

随着对于多层靶板防护结构的深入研究,在保证防护性能的前提条件下,能够尽量减小靶板的面密度也变得极其重要[21]。以第1章中的刚性弹侵彻组合板/金属板的有限元模型为基础,通过更改两层板的厚度改变靶板的面密度,来探究该组合防护结构面密度对其抗侵彻性能的影响。这里需要说明的是组元板只改变了陶瓷和金属边框的厚度,弹簧的大小没有改变,预应力大小为73 MPa。

两层板的厚度范围取为3～6 mm,分别进行组合可以得到16种不同的结果,对应16种不同的面密度,结果如表4所示。防护结构面密度的计算公式为

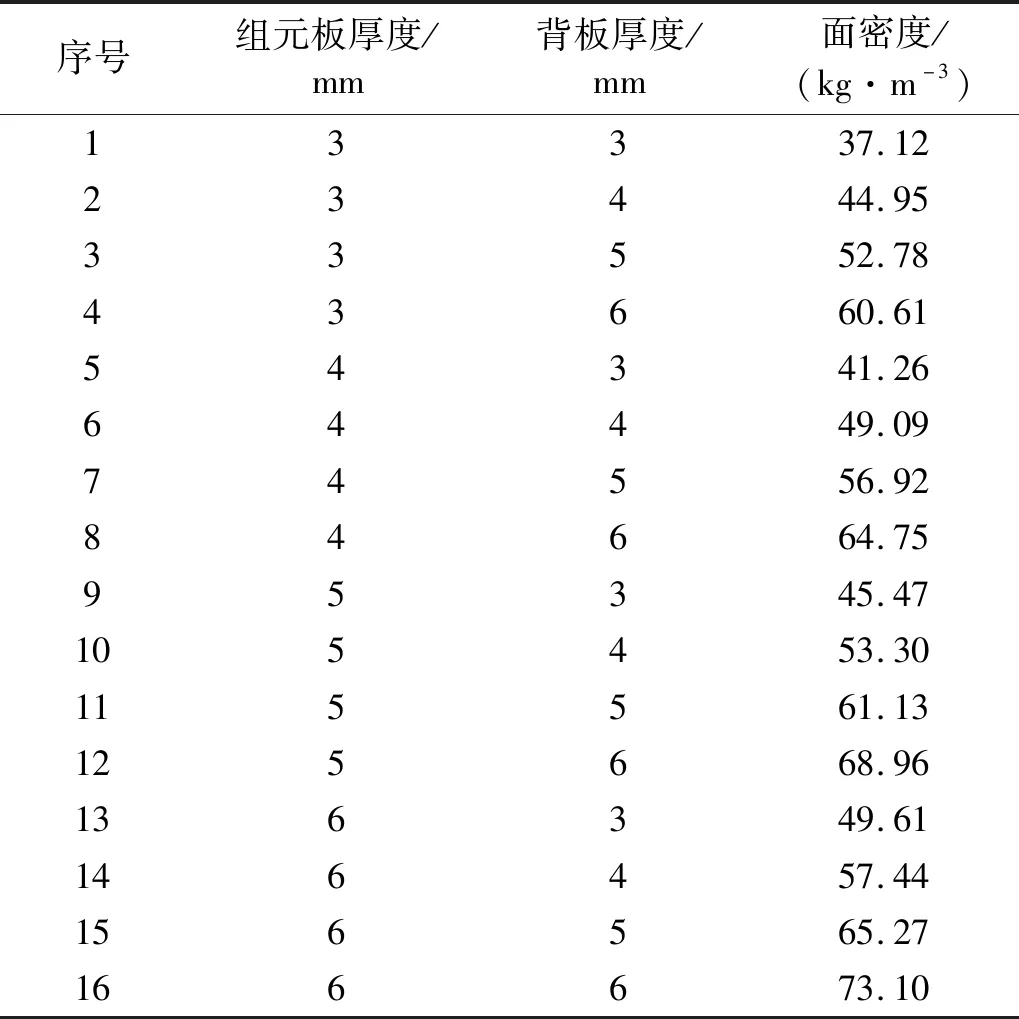
表4 不同靶板配置对应的面密度

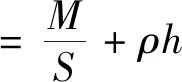
(16)

式中：M为组元板面的总质量;S为组元板面的总面积;ρ为背板的密度;h为背板的厚度。

以子弹的极限穿透速度V50为衡量指标来分析面密度的大小与防护结构抗侵彻能力大小的关系,从图8可以得到：

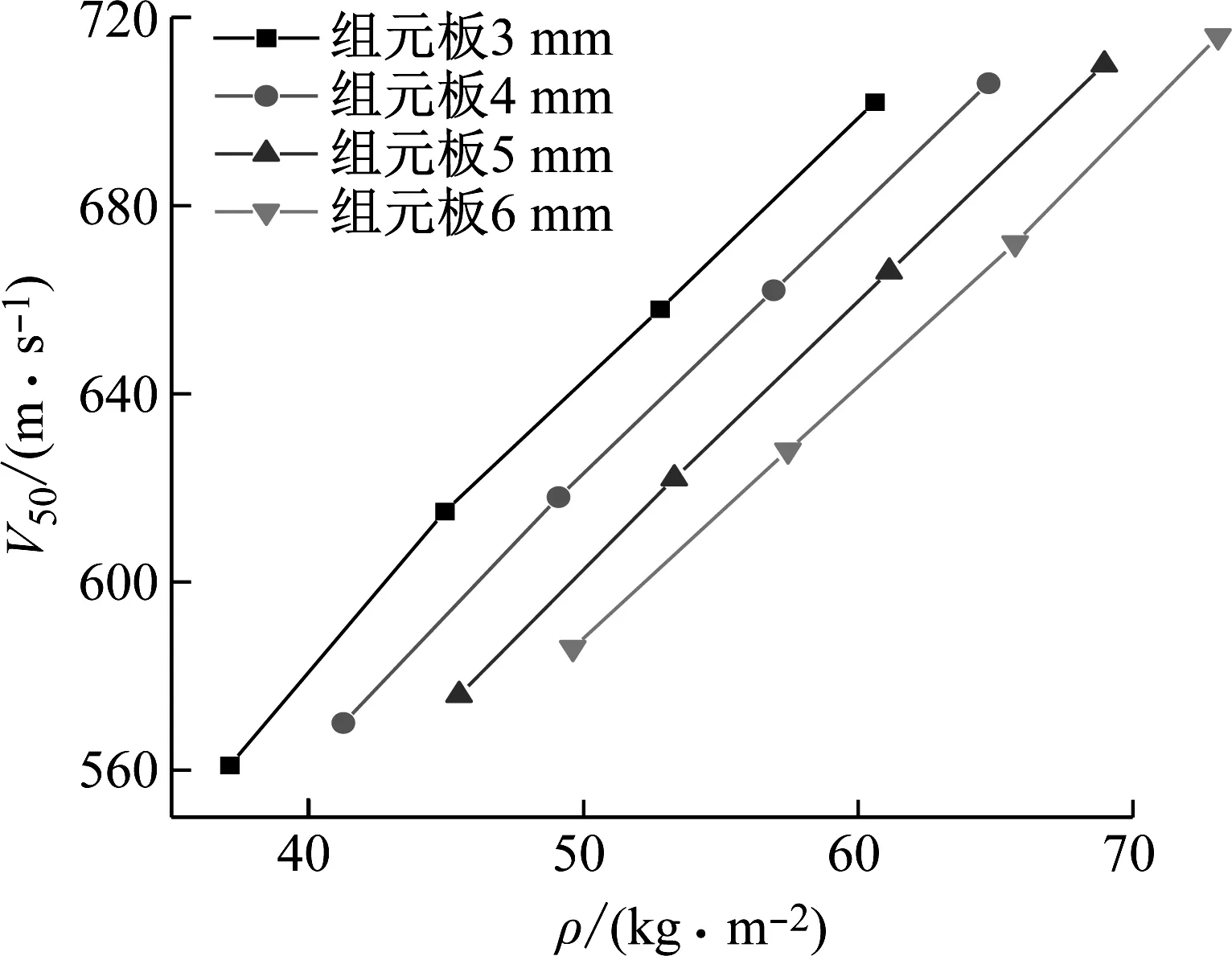
(a) 更改组元板厚度

(1) 随着面密度的增加,子弹的极限穿透速度也随之增大,说明防护结构的抗侵彻能力也随面密度的增大而增强。

(2) 增加背板厚度对应的子弹极限穿透速度的增幅比通过增加组元板厚度对应的极限穿透速度增幅大得多,结构的抗侵彻能力更强。

根据上述结果,考虑材料成本方面等问题,针对同一个问题时,可以通过增加组元板厚度与背板厚度比值,同时施加更大的预应力来达到目的。

3.3 弹体形状的影响

考虑平头弹和卵形弹这两种不同形状的弹体对组合结构的侵彻过程,主要是考虑防护结构对于不同弹体的抗侵彻能力。

对于子弹的设计是保证子弹的质量相同,相同速度下的动能相同。子弹的质量为M=19.8 g,让子弹的直径保持相同,主要通过改变子弹的长度来保证质量相等,子弹的几何模型如图9所示,靶板的配置采用的是3 mm+3 mm的组合,预应力的大小为73 MPa。

从图10不同形状子弹的速度随时间的变化曲线中可以得到以下结论：在同样的冲击速度下,防护结构对平头弹的抗侵彻能力很强,而对卵形弹的抗侵彻能力弱一些。随着冲击速度的增加,两种子弹的残余速度的差值逐渐减小。

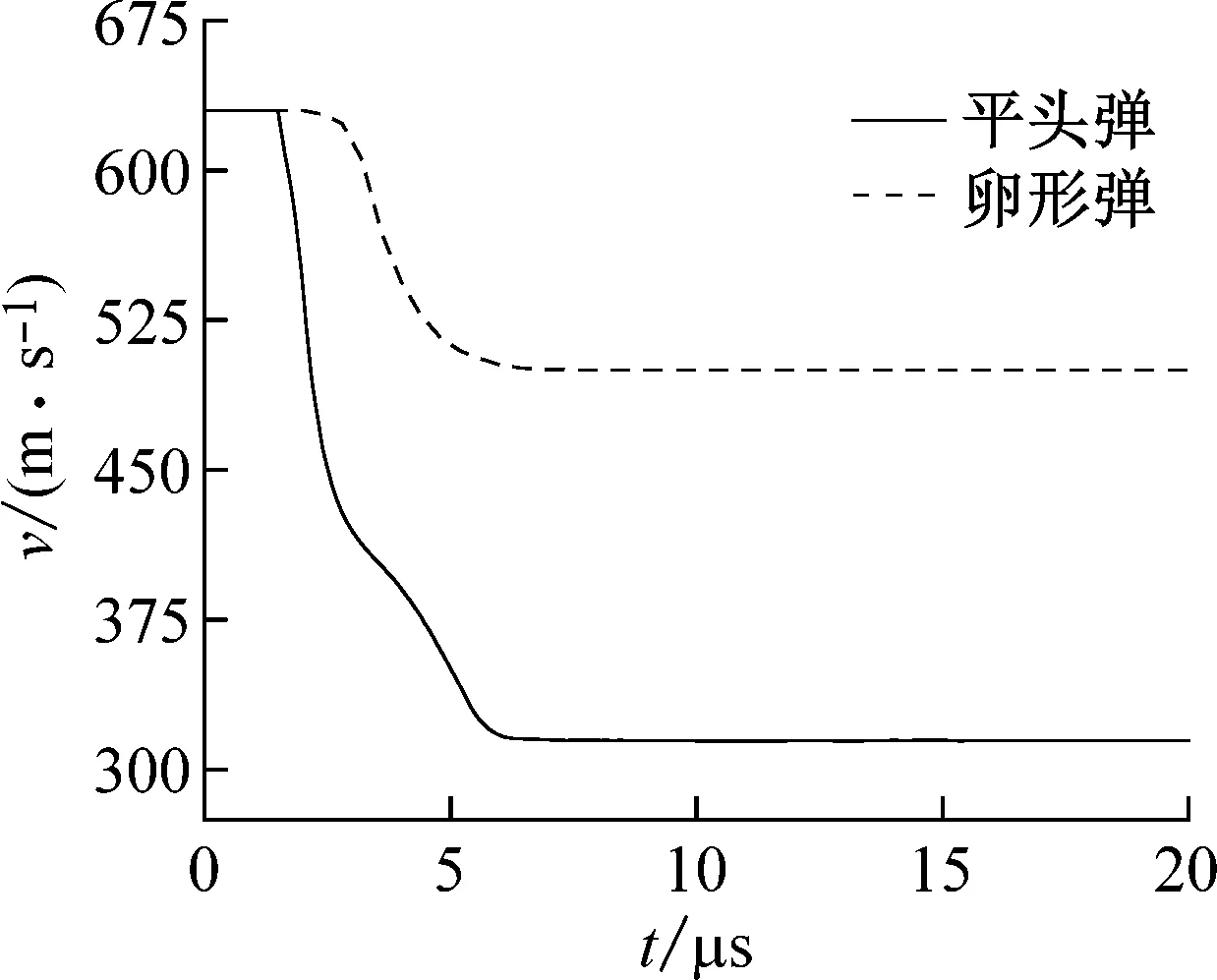
(a) 600 m/s

4 讨 论

基于无量纲分析方法确定侵彻影响因素的经验公式。文献[22-26]中关于侵彻影响因素公式大多是以弹坑深度为因变量的弹坑经验公式,例如侵彻岩石和混凝等一些材料的侵彻深度经验公式,本文考虑的变量是子弹完成侵彻过程后的残余速度。考虑惯性、强度以及可压缩性这3个影响因素。同时考虑到预应力的作用,加入了一项无量纲量——预应力与屈服强度相比。式如(15)所示,ε为金属材料的动态断裂应变,可取为0.2。

4.1 公式的验证

为了验证该公式,参考文献[27]中关于单层金属靶板与双层金属靶板的试验数据来进行公式参数的拟合。考虑到试验数据不包含预应力的影响以及子弹和靶板所使用的材料相同,所以拟合使用的公式忽略了式(15)中的惯性项和预应力项。图11所示即利用公式和试验数据计算得到的结果,可以看出该公式能够很好的拟合试验数据,参数的取值也处于合理范围,说明该公式能够较好地适用于不同情况下的平头弹侵彻过程,具有一定的适用性。适用范围：平头弹,薄靶板,中低速侵彻。

4.2 无量纲参数的拟合

式(15)中临界速度Vc需要进一步确定,其他参数根据材料性质已经能够确定。基于文献[28]提出的经验公式,如式(17)所示。利用数值模拟得到的结果进行拟合计算,得到的曲线以及相关参数如图12所示。

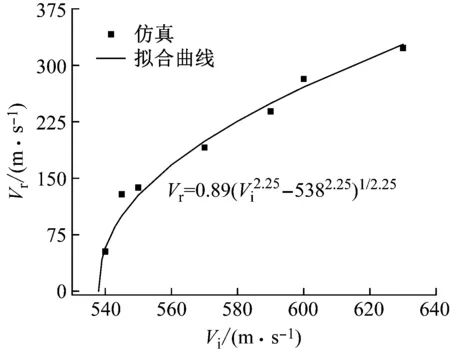
图12 临界速度的拟合结果

Vr=a(Vip-Vcp)1/p

(17)

式中：Vi为冲击初速度;Vc为临界速度;a和p的取值可以通过最小二乘法拟合初始速度和残余速度求得。卵形弹撞击靶板发生扩孔破坏：a=1;平头弹撞击发生冲塞破坏：a<1。

从图11中的拟合结果可以清楚地得到靶板在无预应力条件下的临界速度大小为538 m/s,将其代入式(15)中进行数值仿真计算结果的参数拟合。

残余速度的表达式中的变量为冲击初速度Vp和预应力σ,这里分别讨论了冲击初速度和预应力与参与速度无量纲量之间的关系。图13所示即为利用残余速度表达式进行拟合所得的结果图。表5和表6中为拟合得到的参数结果,分别对应图13(a)和图13(b)。

表5 Vr/Vc与Vp的拟合参数

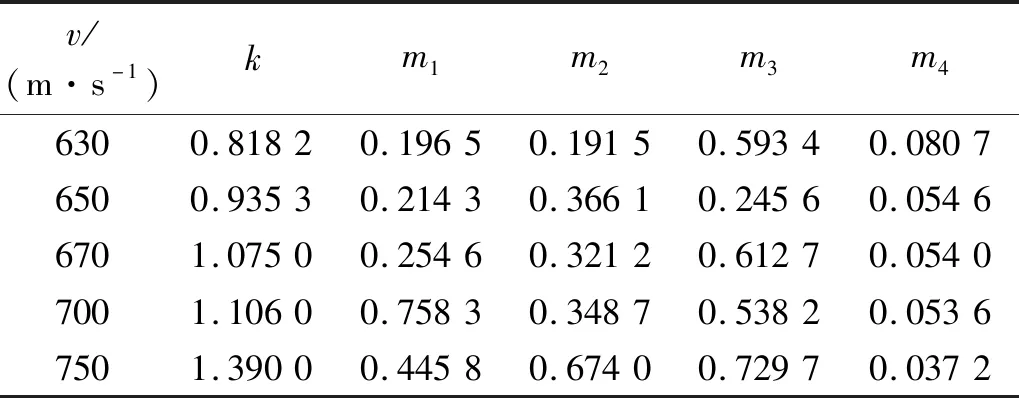
表6 Vr/Vc与σ的拟合参数

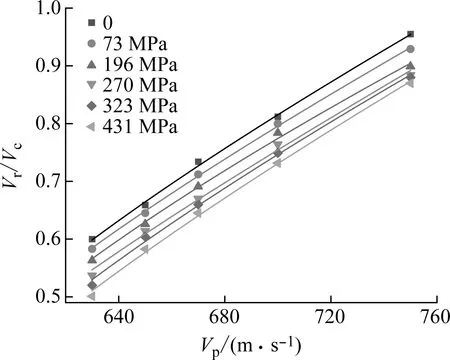
(a) Vr/Vc与Vp的关系拟合结果

从图13可以得知：利用残余速度表达式(15)能够较好的拟合由数值仿真计算得到的侵彻结果。图13(a)表明：对于新型预应力组合结构,不同预应力大小下的曲线趋势大致相同;计算所得残余速度变化趋势近似线性,应该是所选取的速度比临界速度的取值大得多,Vr/Vc的快速上升阶段没有出现。图13(b)表明：不同的初速度下曲线都逐渐趋于平缓,说明预应力对于结构的抗侵彻能力的提升随着预应力的逐渐增大逐渐减小,预应力对结构抗侵彻能力的提升是有效的,但有限度。

通过表5、表6的拟合结果可知：拟合得到的指数参数m均在[-1,1],k的取值在也在合理范围之内。表5表明,随着预应力的增大,预应力无量纲参量项的指数逐渐增大,即预应力的影响增大。表6表明,随着速度的增加,预应力无量纲参量项的指数逐渐减小,这与计算结果是相符的。

5 结 论

提出了一种新型预应力陶瓷组合结构,进行了较系统的有限元数值模拟。本研究适用于平头弹中低速侵彻薄靶板过程。得到的主要结论如下：

(1) 在不同速度的侵彻过程中都表现出相对于无预应力情况,预应力条件下子弹的侵彻残余速度更小,组元板的破坏程度更小,说明结构中添加的预应力能够增强组合结构的抗侵彻能力;随着结构中预应力的增大,子弹的侵彻残余速度逐渐减小,组元板在相同时刻的破坏程度在逐渐减小,结构的抗侵彻能力随着预应力的增加逐渐增强。因此,防护结构的抗侵彻能力随着预应力的增加而增强。

(2) 随着面密度的增加,子弹的极限穿透速度也随之增大。相对于卵形弹,组合结构对平头弹的抗侵彻能力较强;预应力对平头弹的效果也要好一些。

(3) 提出了高速冲击下的残余速度表达式,并结合已有的试验数据进行拟合计算,得到了较合理的参数取值。单层靶板和双层靶板的试验数据拟合较好说明该公式能够适用于不同情况的侵彻过程,具有一定的适用性。分别讨论了冲击速度Vp和预应力σ与Vr/Vc的关系,拟合得到了较合理的参数。结果表明随着预应力的增大,预应力无量纲参量项的指数逐渐增大,即预应力的影响增大;而随着速度的增加,预应力无量纲参量项的指数逐渐减小。