超超临界汽轮机密封非线性汽流激振力影响的转子运动特性

2023-11-14曹丽华高路路司和勇

振动与冲击 2023年21期

曹丽华,高路路,司和勇

(东北电力大学能源与动力工程学院,吉林吉林 132012)

汽流激振是影响机组安全以及限制机组出力的一个主要原因。尤其是近年来超超临界汽轮机组,其密封内的汽流激振作用显著。

汽流激振现象被首次发现在涡轮试验中,Thomas针对该问题提出了简单分析模型[1]。与此同时,美国的Alford[2]提出了间隙激振力的计算公式并指出了效率系数β的取值范围,称该激振力为Alford力。理论研究方面,Muszynska[3]通过理论推导结合试验验证得到了Muszynska流体激振力模型。Iwatsubo[4]考虑周向流动提出单控体模型后,Childs等[5]又考虑了圆周方向面积变化的情况,进行了修正和完善,但是该模型始终存在与试验结果偏差较大的问题。随后Wyssmann等[6]提出了双控制体模型理论,经Childs等[7]修改完善后得以广泛应用。在20世纪90年代,柴山等[8]通过数值解析法构建了汽轮机扭叶片间隙气流激振力的计算公式,且该公式具有较好的普遍适用性。黄典贵等[9]通过合理的运算,得到了汽封内汽流对转子激振力的表达式。随着CFD(computational fluid dynamics)技术的发展,很多学者开始利用这种方法进行研究。李忠刚等[10]通过CFD技术对密封气流流场进行模拟计算,得到了适用于气体流场的Muszynska模型参数。此外,丁学俊等[11]还应用Fluent软件计算了不同迷宫密封的结构对迷宫密封流场的影响并分析了齿角对动力特性的影响。曹丽华等[12]通过正交试验完成汽流激振下转子动力特性的多因素分析,得到影响动力系数的显著因素。在密封转子系统方面,基于汽流激振的研究基础,一些学者开展了将汽流激振力作用于转子系统上的研究,用于分析汽流激振对于转子运动特性的影响。司和勇等[13]为解决传统的非线性激振力模型准确性较低的问题,提出采用Fluent用户自定义函数实现转子多频涡动,进而得到转子的非线性汽流激振力。陈予恕等[14]采用Muszynska密封力模型结合转子-密封系统分析了系统参数对系统稳定性的影响。李松涛等[15]建立密封-轴承-转子系统,研究不平衡量对非线性动力稳定性的影响。崔颖等[16]对实际大型汽轮机转子-密封-轴承系统建立了具有超大规模维数的非线性动力学模型,模拟出转子升速过程中汽流激振现象的典型特征,并得到了系统参数对转子不平衡响应的和稳定性的影响规律。翁雷等[17]通过考虑汽流激振问题时转子裂纹故障分析模型,研究了汽流激振力对裂纹转子系统振动特性的影响。刘思涌等[18]采用Jeffcot模型对转子-密封系统建模,分析系统非线性运动特性。张恩杰等[19]分析了多种因素对密封-转子动力学特性的影响。吴敬东等[20]建立汽轮机低压转子系统的动力学模型,分析随转速变化和径向密封间隙对转子动力学行为的影响。向玲等[21]建立了转子-轴承-密封系统研究了偏心量对系统振动特性的影响。曹丽华等[22]建立实际机组参数的转子-轴承-密封系统,研究汽轮机转子的非线性运动。

当前关于汽流激振对转子-轴承-密封系统非线性运动特性的研究中,主要通过Muszynska模型计算密封汽流激振力,然而该模型中涉及到经验参数的选取,对于不同的物理模型在应用时难以标定经验参数。此外该模型基于静态间隙预测得到,无法考虑转子动态涡动以及流体物性变化等影响,导致非线性强度不足。因此,本文通过CFD建立1 000 MW超超临界汽轮机高压缸隔板密封模型,运用动网格技术和多频涡动模型得到密封非线性汽流激振力,利用MATLAB软件拟合密封非线性汽流激振力,并将有效的拟合激振力嵌入转子运动方程中,构建包含非线性油膜力的转子-轴承-密封系统的运动耦合模型,采用Runge-Kutta法求解微分方程组,实现密封流场内部流动与转子运动的耦合求解。在此基础上,研究非线性密封汽流激振力对超超临界汽轮机转子-轴承-密封系统运动特性的影响。

1 转子-轴承-密封数学模型

基于单圆盘刚性对称Jeffcott转子模型,考虑油膜轴承的作用,对超超临界汽轮机高压转子模化,建立转子-轴承-密封系统如图1所示,研究非线性汽流激振力对圆盘运动的影响。图1中：O1,O2分别为轴承和圆盘的几何中心;O3为转子的质心;转子两端由滑动轴承支承;Fx,Fy分别为轴承x,y方向的非线性油膜力;Fax,Fay分别为x,y方向的激振力;圆盘与轴承之间为无质量弾性轴。

图1 转子-轴承-密封系统示意图

1.1 非线性汽流激振力模型

结合1 000 MW汽轮机高压缸隔板密封的实际参数建立隔板密封模型如图2所示,其中参数如表1所示。

表1 模型参数表

图2 高压缸隔板密封剖面示意图

建立如图3所示的物理模型,采用ANSYS ICEM划分block结构网格。利用Fluent计算非稳态流场,边界条件采用进出口压力边界,并根据各负荷对应的蒸汽参数进行设置。计算过程中为考虑汽流激振力的非线性特征,基于高等转子动力学构建转子的多频涡动模型。涡动方程[23]如下

图3 物理模型及网格

(1)

(2)

式中：Cr为转子初始偏心量,mm;x′(t)和y′(t)分别为x和y方向上速度,m/s;Ω为公转涡动速度,rad/s;t为时间,s;下标“j”为转子涡动时的对应的频率,考虑到汽轮机转子旋转对应的频率,涡动频率选取了5～60 Hz,共12个频率点。

由于转子涡动会引起网格流域变化,使用动网格技术结合用户自定义函数UDF(user defined function)定义转子运动轨迹,在保证良好的初始网格前提下,采用平铺和弹顺光滑两种网格更新手段。

基于上述方法得到随涡动频率和偏心量变化的非线性密封激振力如图4所示。通过MATLAB软件幂次拟合构建非线性激振力的拟合模型,表达式如下

(a) Fax

Fax=f(Cr,Ω)

Fay=f(Cr,Ω)

(3)

式中,Cr为偏心量。

1.2 非线性油膜力模型

根据文献[24]所运用的非线性油膜力计算模型,在x,y方向上的无量纲油膜力为

(4)

其中

G(x,y,α)=

(5)

(6)

式中：x,y,x′和y′分别为轴承无量纲位移、速度;L为轴承的长度;R为半径;s为Sommerfeld修正系数;P为转子质量的一半,kg;μ为润滑油黏度,Pa·s;b为轴承径向间隙,mm。

1.3 转子-轴承-密封系统运动微分方程组

设转子左端轴承处的径向位移为x1,y1;圆盘处的径向位移为x2,y2;m1,c1和m2,c2分别为轴承和圆盘的等效集中质量和结构阻尼;e为圆盘的质量偏心距;ω为转子角速度,rad/s;c为密封间隙,mm;g为重力加速度,m/s2。建立转子-轴承-密封-系统运动微分方程组如下

(7)

令

τ=ωτ,X1=x1/b,Y1=y1/b,

X2=x2/c,Y2=y2/c,

将非线性油膜力、非线性密封汽流激振力代入,并对其进行无量纲变换得

(8)

1.4 模型验证

以往对于密封非线性汽流激振力的计算是采用Muszynska模型,具体的计算表达式为

式中：K,D,mf分别为密封系统的刚度、阻尼、质量;K,D,τ为关于位移的非线性函数,其表达式为

D=D0(1-e2)-n,K=K0(1-e2)-n,τ=τ0(1-e)b1

为验证本文模型的有效性,采用间接验证的方法。首先利用数值模拟得到不同偏心量以及涡动频率对应的非线性激振力作为基准,分别用Muszynska模型和非线性汽流激振拟合模型在相同条件下进行计算,验证结果如表2所示。

表2 误差对比验证表

表2中的数据表明,利用非线性汽流激振拟合模型所得结果对应的误差最小为2.22%,而Muszynska模型所得结果对应的误差最小为20.31%,并且小偏心范围内非线性汽流激振力拟合模型的计算误差要远远小于Muszynska模型。这是因为Muszynska模型中涉及到经验参数的选取问题以及该模型对于流体周向运动的过度预测,使得该模型对于激振力的计算产生较大偏差。而非线性汽流激振力拟合模型主要是由于密封非线性激振力具有较强的非线性变化所导致拟合过程中产生的误差。然而,该拟合模型相比于以往的Muszynska模型仍具有较好的准确度。

2 计算结果及分析

基于有效的密封激振力拟合模型,本文利用MATLAB软件采用变步长Runge-Kutta法对二阶微分方程组进行求解。系统参数如表3所示。

表3 方程主要参数

2.1 密封激振对系统运动特性的影响

汽轮机冲转升速过程的分岔图以及不同转速下的轴心轨迹图,如图5所示。系统在非线性油膜力和质量偏心力的作用下依次经历了一周期运动、复杂运动、单周期运动,在临近额定转速时系统位移散点收敛于一定范围之内。由图5可知,系统在50～100 rad/s期间经历复杂运动后进入单周期运动。这主要是由于非线性油膜力对系统运动的影响起主导作用所引起的系统失稳,系统非线性较强。随着转速升高,在150～200 rad/s(临界转速附近)系统响应值较大幅度跳跃,这是随着转速升高,质量偏心力与非线性油膜力耦合从而引发系统产生强迫振动,诱发系统失稳。

汽轮机在运行转速内,压比对密封激振力的影响较大,并且随着负荷的升高,加剧了压比对于激振力的影响程度,从而影响系统稳定性。不同压比对应系统的三维分岔图,如图6所示。由图6可知,在初始负荷时,不同压比之间分岔图中均只有一条“点带”,在此期间系统经历多种运动的交叉。随着负荷的增加,不同压比对应的系统均进入混沌运动,10%THA～70%THA系统的响应幅值在0.219 5左右波动,70%THA之后,当压比由1.01增加到1.03时,对应的分岔图中图形逐渐发散,当压比增加到1.05时,分叉图中散点汇聚形成两个集中区域,系统进入混沌“二周期”运动并且随着压比增大波动幅度增加。说明在低负荷时,汽流激振对系统的影响较小,随着负荷的增加,汽流激振的影响力逐渐增大,而压比的增大使得密封腔内流体流速增加,密封的节流效应减弱,加剧了负荷对于汽流激振现象的影响,使得系统的振动特征发生明显变化。

不同压比对应系统的三维频谱图及局部放大图,如图7所示。由图7(b)可知,在30%THA～50%THA时,不同压比对应系统的振幅值大致相近,说明在低负荷时压比对汽流激振的影响力较小,系统的频谱特征相似。随着负荷升高,1.01压比对应系统的幅值变化较小,至额定负荷运行时,1/2工频分量才有所增加的同时衍生出1/3和2/3工频分量;当压比增大到1.03时,系统从80%THA开始,1/2工频幅值激增,随着负荷升高至额定负荷之后,对应的幅值增大到约为1.01压比的2倍左右;随着负荷增加,压比为1.05对应系统的幅值变化最为明显,当负荷由60%THA向满负荷升高时,1/2工频幅值断崖式增大,而且出现最为明显的1/3和2/3工频分量,在超负荷运行时,重频现象更加突出。

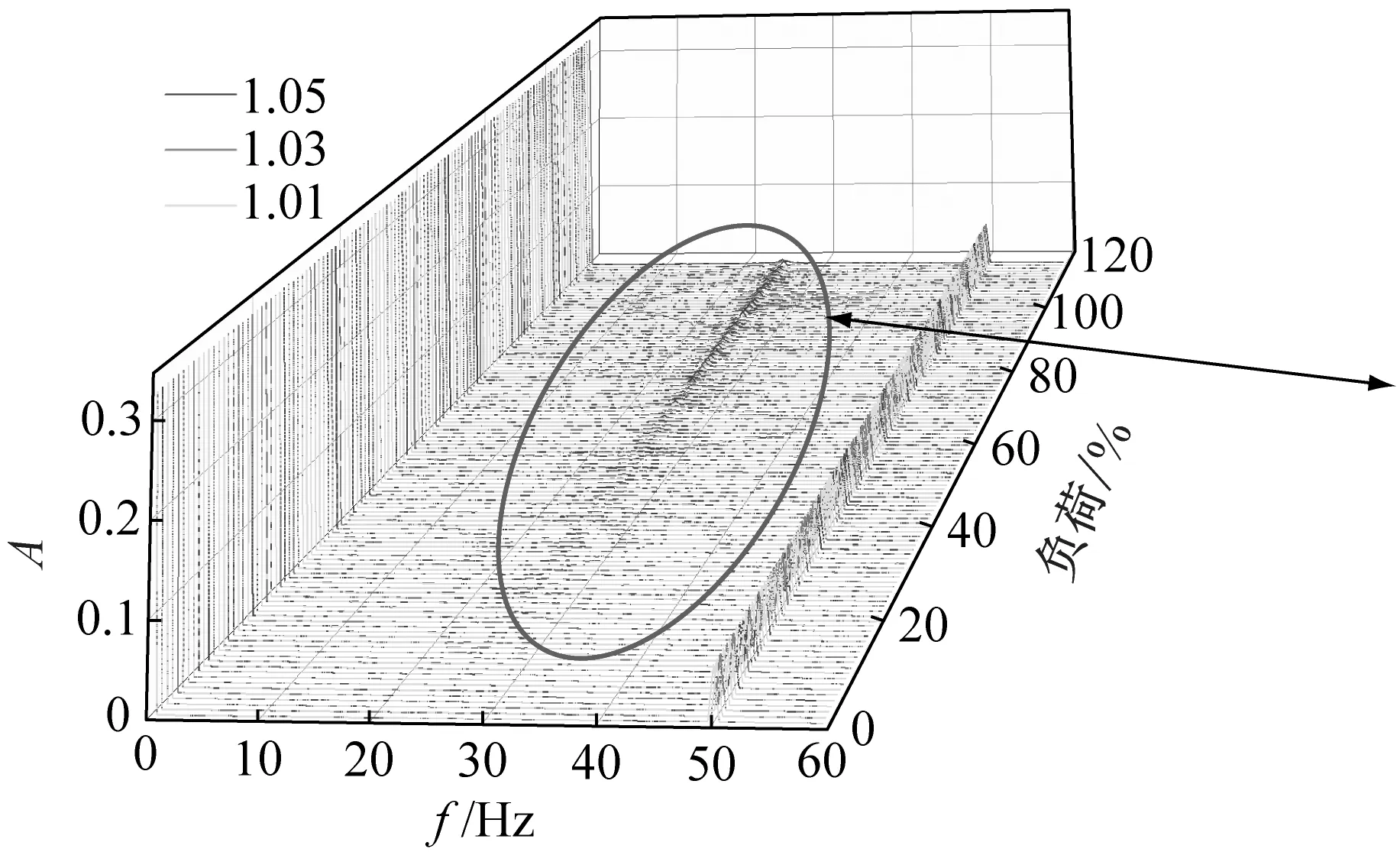
图7 不同压比三维频谱图及局部放大图

不同压比主要频率的无量纲振幅图,如图8所示。由图8可知,20%THA之前系统主要以工频振动为主。随着负荷的升高,汽流激振的影响开始显现,1/2工频分量逐渐明显的同时衍生1/3和2/3工频分量。80%THA以后,1/2工频振动的幅值大幅度增加,这种现象在压比为1.01～1.03较为明显。可以看出随着压比的增加,提前了1/3和2/3工频分量的出现,并且随着负荷的升高,压比越大,对应的幅值跳跃程度增加。这是由于本文综合考虑了非线性油膜力、重力、质量不平衡力以及非线性汽流激振力,低负荷时主要是由非线性油膜力以及质量不平衡力主导引发自激振动,出现1/2工频振动。随着负荷的增加,由于泄漏量增大使得汽流激振的影响力增大,汽流激振引发低频振动,系统1/2工频分量增大并衍生出1/3工频和2/3工频分量。而压比的增大,增加了同一负荷密封腔内的泄漏量导致汽流激振现象愈加严重,使得系统所受的横向汽流激振力增加,从而引发系统严重失稳。

2.2 非线性汽流激振力对系统稳定性的影响

最大Lyapunov指数是衡量转子动力系统稳定性的一个重要定量指标。为研究非线性汽流激振力对系统稳定性的影响,本文采用wolf法计算转子系统的最大Lyapunov指数,如图9所示。图9(a)中,初始负荷时不同压比对应的系统均经历周期、拟周期和混沌交叉运动,说明负荷较小时汽流激振对系统稳定性的影响较小,系统的非线性较弱系统较为稳定。随着负荷的增加,汽流激振的影响增强,同一压比下,由于汽流激振力的强非线性,指数响应值无规则跳跃。在相同负荷区间内,随着压比的增加,指数响应值跳跃幅度增加,结合图9(b)不同压比平均指数图,当压比由1.01增加到1.03时,平均指数值增加10.3%,压比由1.03增加到1.05时,平均指数值增加4.3%,说明压比越高,系统混沌性越强,系统稳定性越弱。