基于DnCNN声音增强的高坝泄流微弱空化声音信号识别与提取

刘 昉,王润喜,庞博慧,练继建,梁 超

(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300072;2.华能澜沧江水电股份有限公司,昆明 650214)

高坝大库工程是水资源综合利用和水能资源开发的需要。汛期泄洪期间,明流洞室、溢洪道等过水建筑物的水流流速往往可达40～50 m/s,当高速水流流经不平整的壁面时,边界压强的骤然变化极易引发空化现象,空泡溃灭后激发的微射流会不断地剥蚀壁面,造成流道的空蚀破坏,从而对水工建筑物的安全稳定运行产生极大的威胁。

空蚀现象同样广泛地存在于离心泵、水轮机等水力机械领域,相对于水力机械,科研人员对于过水建筑物空蚀破坏和空蚀监测的研究较少[1-2],相关的研究尚不成熟。工程界对空蚀的重视和研究始于1935年巴拿马麦登坝输水道进水口的严重空蚀破坏事故[3]。空化噪声是空化空蚀现象的重要物理特征,空化噪声谱为连续宽带谱,且具有独特的频谱结构[4-5],明显异于流道内其他泄流噪声,科研人员对不同水流工况下空化噪声特性的研究始于20世纪50年代,并逐渐形成了根据空化声信号进行空化监测的音频监测方法[6]。现今多通过监测流道内过流噪声声压级或功率谱级的变化来判断空化空蚀现象的发生[7-8],当声压级或功率谱级发生较大的跃升时则认为空化已经发生,并根据跃升的幅度判断空化发展程度。然而高坝泄流时泄洪洞、溢洪道等过水建筑物出口处,泄流冲击、碰撞会激发出含有巨大能量的泄流噪声,强泄流噪声会对空化声信号的采集和识别产生十分不利的影响,使得监测信号信噪比偏低,甚至将空化声信号完全淹没。当监测结果能够识别出明显的空化信号时,空蚀空化破坏极有可能已经发展到了较为严重的程度。在强泄流噪声的干扰下,如何从较低信噪比的音频监测信号中识别并提取出相对微弱的空化声信号是一个亟待解决的问题。此外,在低信噪比条件下空化声信号与泄流噪声在中低频段存在着严重的频带重叠问题,使用传统的FIR(finite impulse response)滤波器、小波分解和经验模态分解等很难将泄流噪声有效地去除,还会引入大量的假定条件和不确定参数,难以保证去噪后空化声信号的真实性和可靠度,尤其是空化声信号的频谱结构特征可能会大量丢失。

语音增强是指将带噪语音中的噪声滤除、从中提取出干净语音以提升语音质量和可懂度的技术[9]。语音增强通过保留干净语音信号的时频特征和频谱结构等,力求保留语音中的完整信息,从实现过程和目的上看,空化声信号的识别与提取和语音增强本质上并无区别,因而语音增强方法在空化声信号的识别与提取中也应具有一定的适用性。宽带噪声是语音增强着力消除的干扰之一,与泄流噪声类似,宽带噪声和语音信号之间也存在着严重的频带重叠问题,以谱减法[10]为代表的一类语音增强方法在处理此类问题时具有独特的优势。在此基础上,Xu等[11-12]提出了基于回归深层神经网络(deep neural network,DNN)的深度学习语音增强方法,该方法以带噪语音信号的对数功率谱作为模型的输入特征[13],通过深度神经网络完成语音信号的提取过程,避免了以往方法中的种种假设,使网络模型充分学习带噪信号与纯净信号之间复杂的非线性映射关系,最终获得了更高质量和可懂度的语音增强结果。该方法在空化声信号的识别与提取中有着巨大的潜力,但是语音信号与空化声信号存在着较大的差异,还需进一步的改进。

降噪卷积神经网络(denoising convolutional Neural Network,DnCNN)是由Zhang[14]等提出的图像去噪卷积神经网络,因其独特的网络结构,可以对随机噪声起到较强的抑制作用,已被广泛应用于海洋噪声和沙漠噪声等随机噪声的去除[15-18]。由于泄流噪声也是一类典型的随机噪声,因此在本文算法中引入DnCNN以提高空化声信号识别与提取的准确度和效率。同时,作为一种深度网络模型,DnCNN还具有能够高效处理海量数据的优点,这为采样频率达到44.1 kHz的声音信号的有效分析提供了保障。

由此,本文基于深度学习语音增强方法并结合DnCNN网络模型提出了基于DnCNN声音增强的空化声信号增强方法,对该方法的原理进行了阐述并通过试验对其增强效果进行了验证,以期为高坝泄流过程中微弱空化声信号的识别与提取提供一种可靠的解决方案。

1 基于DnCNN的空化声信号增强方法

本文提出的基于DnCNN声音增强的空化声信号增强方法在传统语音增强方法的基础上,将深层神经网络DNN替换为对随机噪声抑制能力更强的降噪卷积神经网络DnCNN,将短时傅里叶变换(short-time Fourier transform,STFT)引入特征提取模块,使用对数功率谱表示的时频图作为网络模型的输入,其具体实现流程如图1所示。

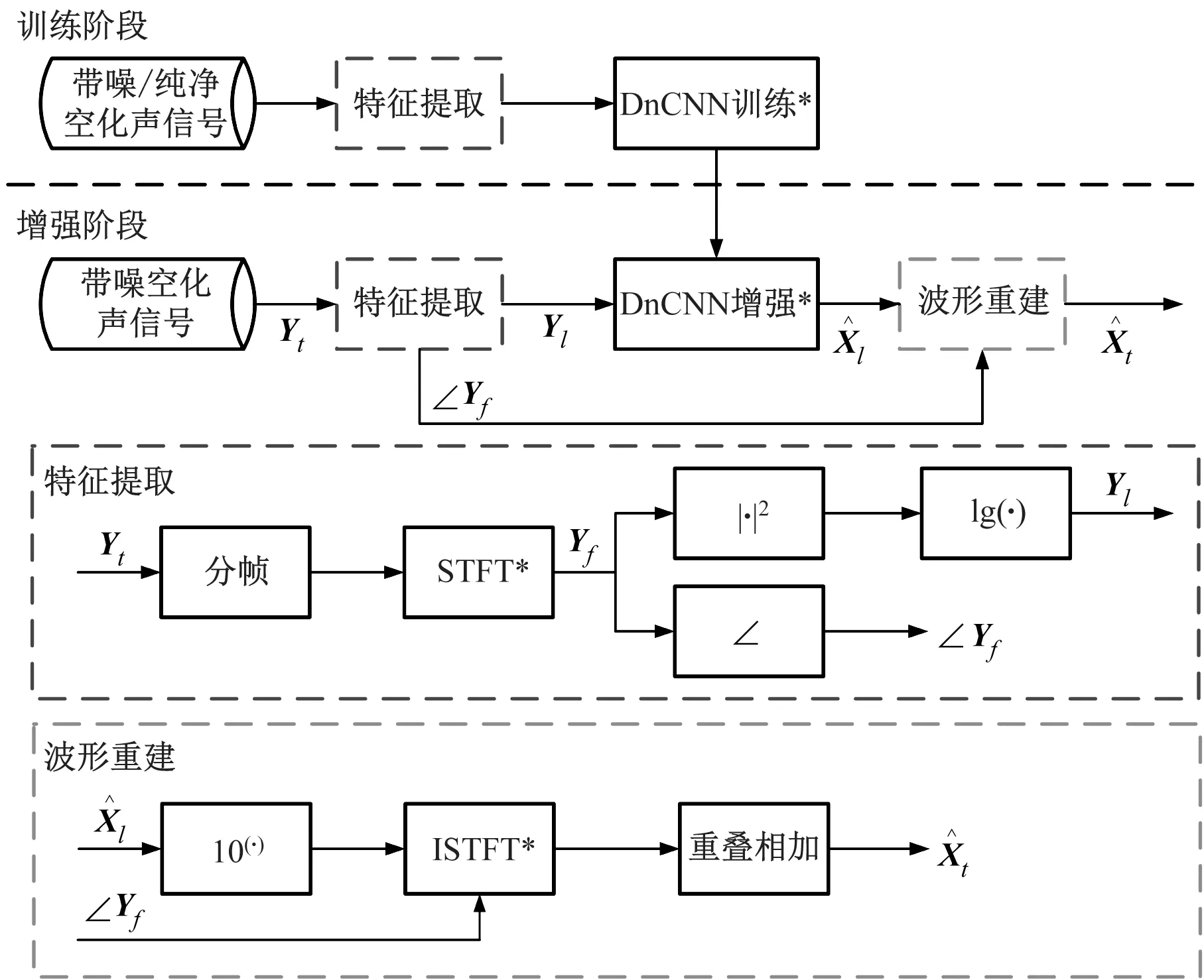
图1 空化声信号增强方法流程

该方法基于谱减法的最基本假设,即带噪空化声信号Yt为空化声信号Xt与强泄流噪声信号Nt的时域相加,空化声信号Xt和强泄流噪声信号Nt互不相关

Yt=Xt+Nt

(1)

对式(1)两端做傅里叶变换并平方可以分别得到谱减法在频域的幅度谱表示和功率谱表示[19],如式(2)和式(3)所示

Yf=Xf+Nf

(2)

(3)

式中,Yf,Xf,Nf分别为带噪空化声信号、纯净空化声信号和泄流噪声信号傅里叶变换后的结果。式(3)也可以写为

(4)

对式(4)中的每一项都取10的对数并作逆运算,则可以得到谱减法的对数功率谱表示

10Xl=10Yl-10Nl

(5)

式中：Yl,Xl,Nl为分别对带噪空化声信号、纯净空化声信号和泄流噪声信号的功率谱取10的对数的结果。由式(1)～式(5)可知该方法的核心在于在频域内通过对带噪信号功率谱的变换操作,实现噪声的去除和目标信号的增强。

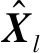
2 DnCNN网络结构

DnCNN由多个卷积层Conv(convolutional)、批量标准化层BN(batch normalization)和激活函数层ReLU级联而成。批量标准化的使用解决了训练过程中内部协变量移位的问题,加快了模型的训练过程,避免了梯度消失的问题[20],同时引入残差学习[21],保证了模型在深层次网络结构下的性能不发生退化,多种优化方法的使用最终保证了DnCNN去除随机噪声的优秀能力。DnCNN的去噪原理如式(6)所示

y=x+v

(6)

理想的无噪声图像为x,图像的每个像素都有一个噪声偏移量,构成噪声图v,y则为添加了噪声后的图像,模型的主要任务便是根据带噪图像y,恢复出干净的图像x的过程。若以灰度图像作为模型的输入,则输入形式为二维矩阵,矩阵上的每个值都表示图像上对应像素点的灰度值,矩阵的两个维度分别表示图像的宽和高。恢复干净图像的过程也就是通过带噪图像灰度值矩阵变换得到干净图像灰度值矩阵的过程。一段信号经过时频变换后也可以转化为二维矩阵,即时频图,时频矩阵的值表示信号的功率谱,矩阵的两个维度分别表示频率和时间。可以发现,分别以灰度图像和时频图作为DnCNN模型的输入时,式(6)所表示的过程与式(3)表示的过程几乎完全一致。本文对DnCNN进行了改进以将其应用于泄流噪声的滤除,从而实现空化声信号的增强。其网络结构如图2所示。

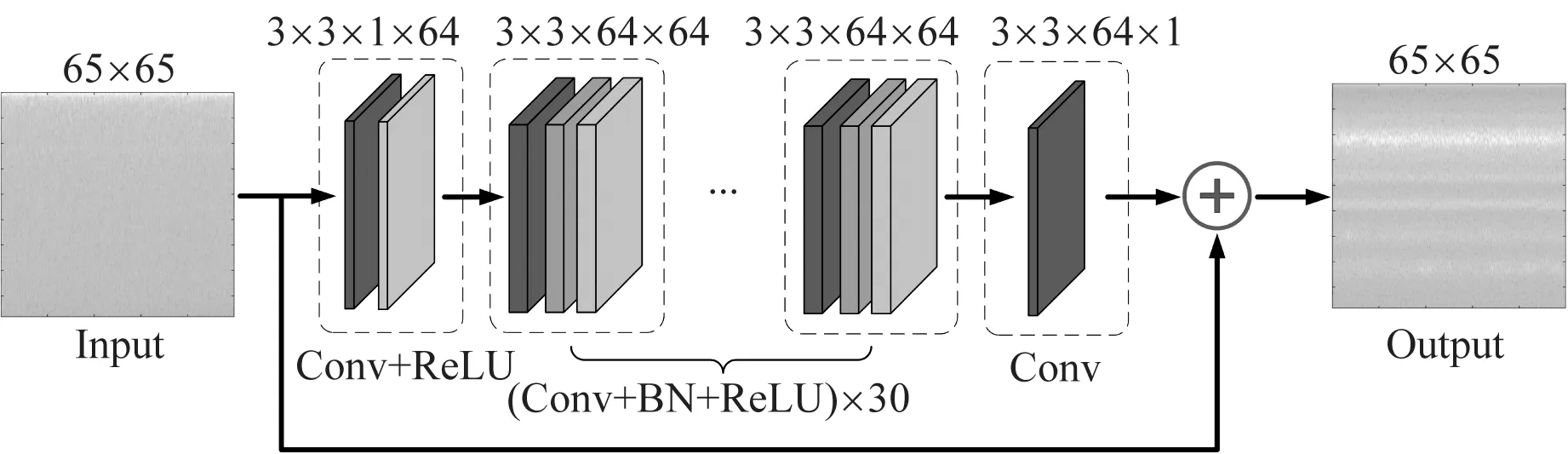
图2 DnCNN网络结构

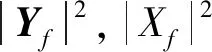
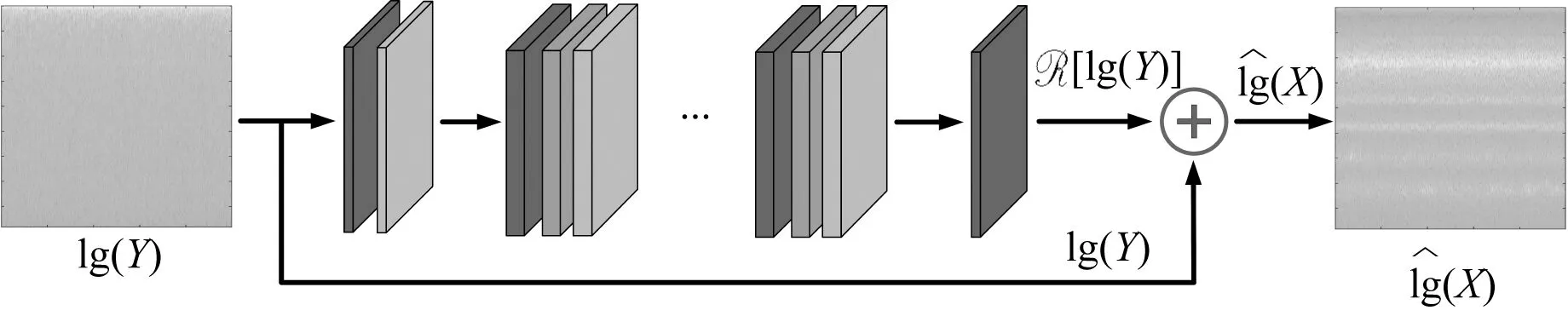
图3 模型内部数据变换过程

图3中,R(·)为模型中卷积神经网络部分的变换过程,首先结合式(3)可知

Y=X+N

(7)

两边同时取对数可得

lg(Y)=lg(X+N)

(8)

等式右端做分离即可得到

(9)

(10)

所以R[lg(Y)][22]即为

(11)

那么以对数功率谱作为模型的输入时,DnCNN实现空化声信号增强的过程为

(12)

3 试验分析

3.1 数据采集和预处理

DnCNN网络模型的训练是应用空化声信号增强方法的关键,模型训练所需的数据集由空化声信号和泄流噪声信号构成,两类数据均依托室内试验进行采集,采集设备选用INV3068多功能动态信号采集仪和INV9204型高声压传感器,采集软件为采集仪配套DASP V11软件,INV3068工作采样频率0.1 Hz～250.0kHz,INV9204最大声压级154 dB,频响范围20 Hz～50 kHz。试验过程中采样频率均设定为44.1 kHz。

为了初步验证空化声信号增强方法的可行性,满足DnCNN模型训练所需的数据量要求,空化声信号的采集通过空蚀试验进行。试验平台为KJ-1000超声磁致伸缩仪,磁致伸缩仪通过变幅杆产生高频的振动使液体中出现周期性的高压与低压,导致液体中出现较大的负表面张力,从而使得试件表面在短时间内出现强烈的空蚀[23],激发出空化声信号。试验过程中,通过调节输出功率控制磁致伸缩仪的振动频率,由人耳通过噪声的变化凭借经验判断空蚀现象的发生。空蚀现象发生后,待磁致伸缩仪工作状态稳定时,采集空化声信号。磁致伸缩仪空蚀试验装置示意图及现场采集照片如图4所示。

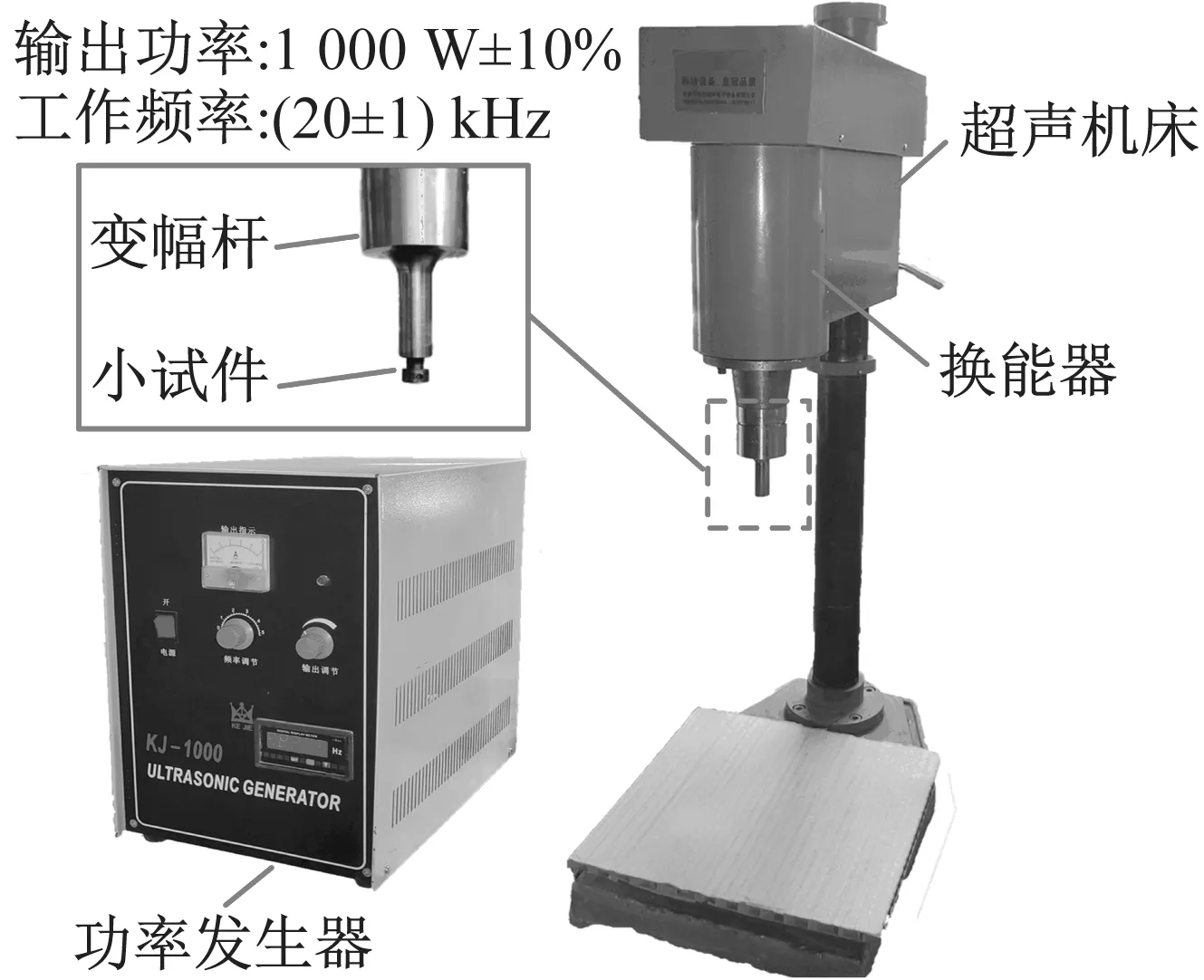
(a) 磁致伸缩仪空蚀试验装置示意图

泄流噪声的采集通过水工模型泄流试验进行。试验平台为某水利枢纽1∶60水工模型,试验工况为千年一遇洪水,上游设计洪水位627.52 m、下游水位472.75 m,溢流表孔、泄洪中孔、排沙底孔联合运用,闸门全开,开敞泄洪。某水利枢纽水工模型及现场采集照片如图5所示。

图5 某水利枢纽水工模型及泄流噪声采集

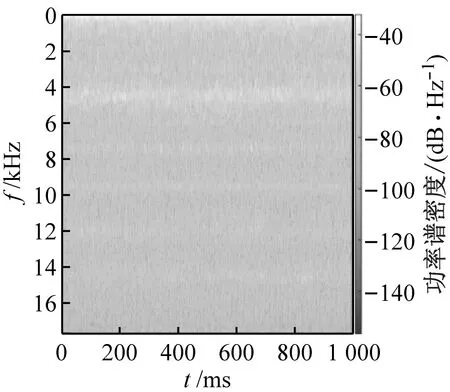
对采集到的空化声信号进行频谱分析后发现,对应磁致伸缩仪工作频率的高频部分出现了异于典型空化噪声谱的能量集中现象,如图6所示。信号的峰值能量明显地集中于空蚀试验时磁致伸缩仪的工作频率18.95 kHz左右,说明在采集信号中有对应该频率的高能噪声存在,该噪声可能由两部分构成：一方面是在磁致伸缩仪的激励下,试件与水体规律地相互作用激发出的对应磁致伸缩仪工作频率的噪声;另一方面是伸缩仪运行时机器自身的振动噪声。高能噪声的存在对采集空化声信号的波形产生了严重的影响,且空化噪声谱属连续宽带谱,该噪声与所需空化声信号在对应频段内也存在重叠问题,所以必须对其进行处理以消除影响。

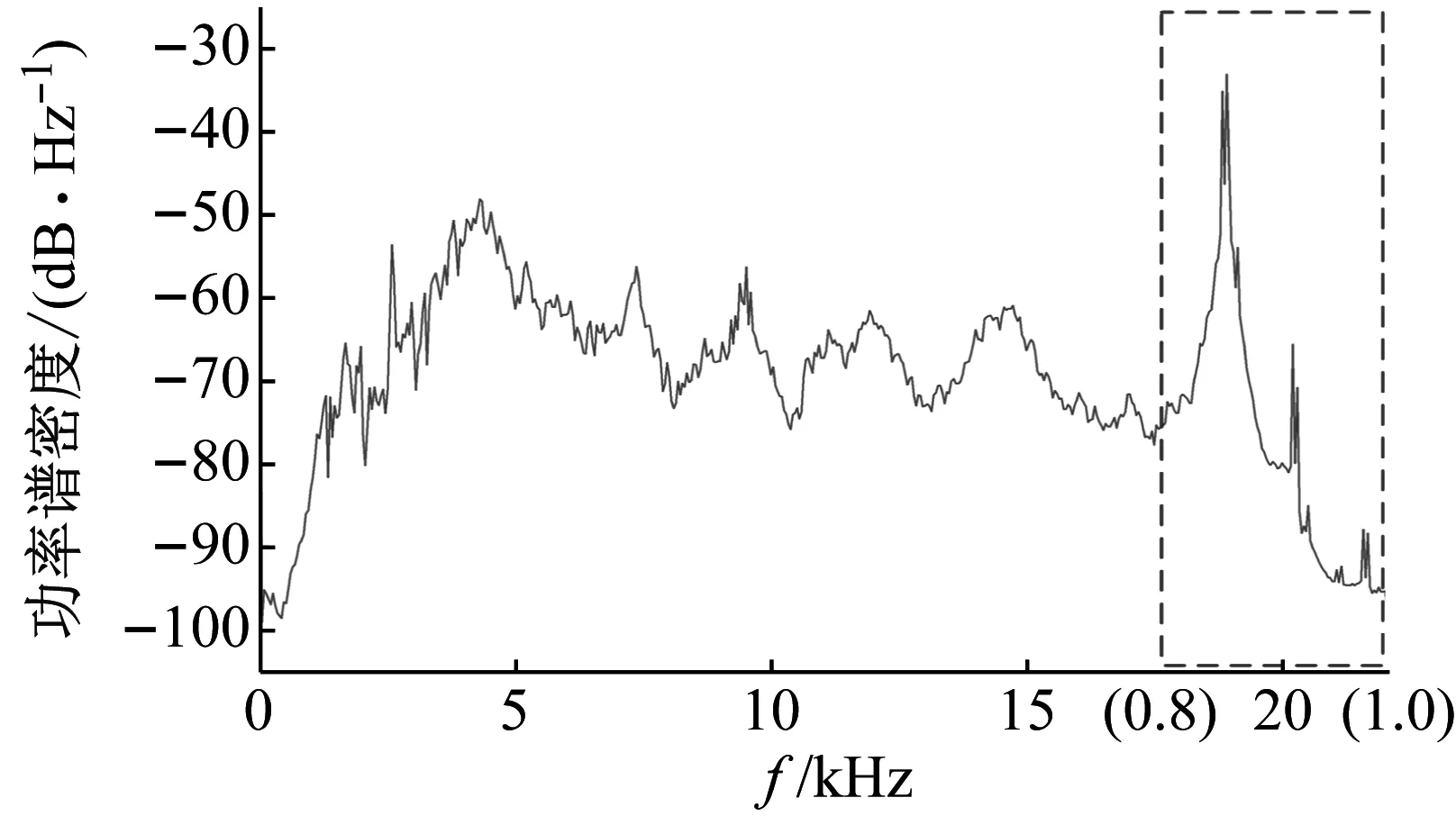
图6 采集空化声信号功率谱密度图

除试验工况外,采集了伸缩仪在相同运行工况下机器自身的振动噪声,使用谱减法对其进行去除后发现,采集信号的能量集中现象并未得到有效的缓解,表明试件与水体相互作用激发的噪声是构成高能噪声的主要部分。然而通过改进试验、数字滤波等手段无法很好地避免或剔除该噪声、完整地保留所需空化声信号。为了客观地评价本文提出的空化声信号增强方法,避免高能噪声对试验结果的影响,遂对采集到的空化声信号进行滤波处理,滤去采集信号含有噪声的高频部分,只保留归一化频率为0～0.8内的空化声信号,并对滤波后的信号进行重采样处理,重采样频率取原采样频率的0.8倍,即35 280 Hz。经滤波重采样处理后空化声信号的频谱曲线如图7所示。

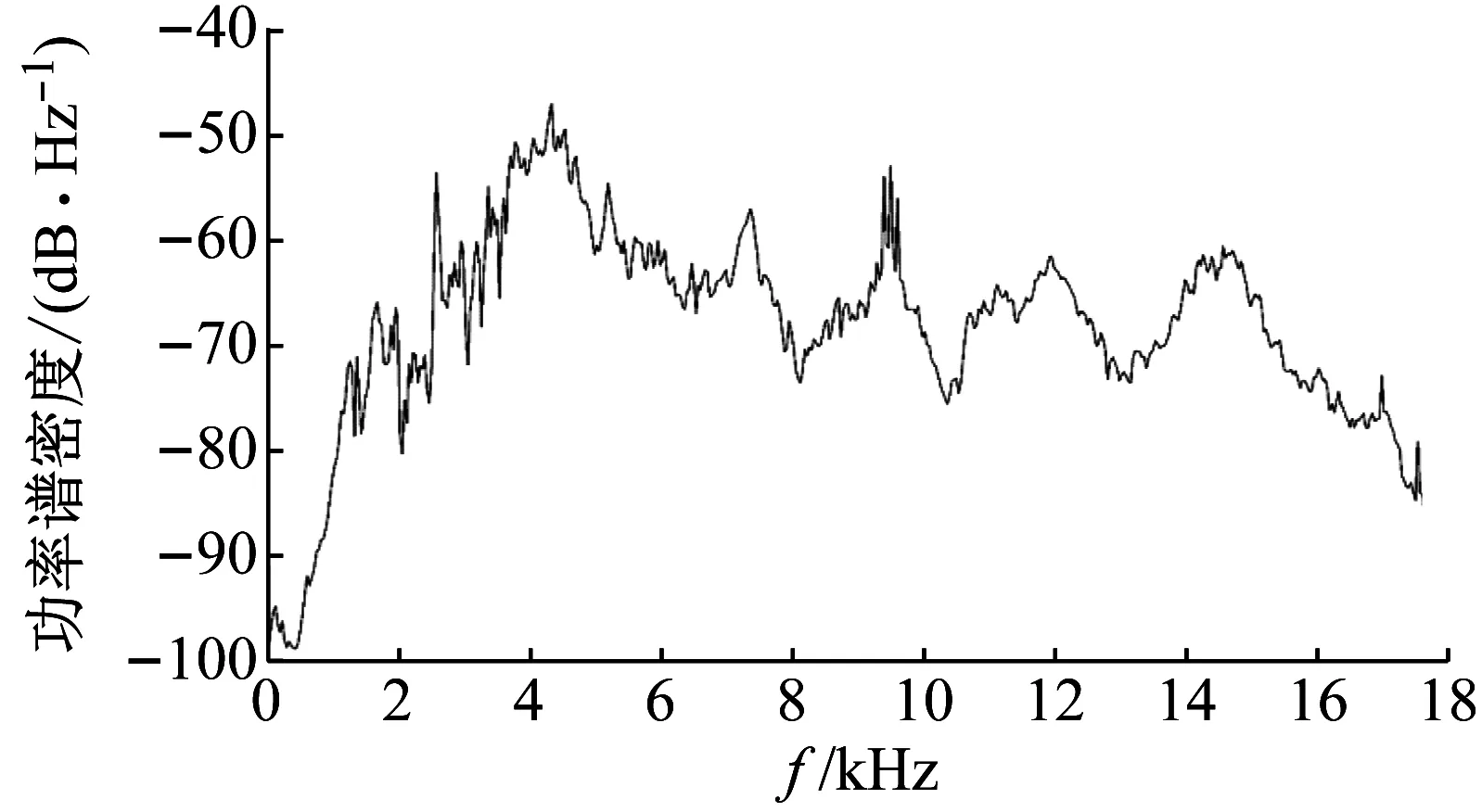
图7 处理空化声信号功率谱密度图

为保证空化声信号与泄流噪声信号采样频率的一致,对采集到的泄流噪声信号进行同样的滤波和重采样处理。下文中提到的采样频率均指重采样频率35.28 kHz。

3.2 数据集构建

从处理后的试验信号中截取出1段长约5 min的空化声信号作为纯净信号,截取出3段长约5 min的泄流噪声信号作为噪声信号,将纯净信号分别与3段噪声信号依次按照-5 dB,-10 dB,-15 dB,-20 dB的信噪比进行混合,最终生成了12段共计长约1 h的带噪空化声信号。得到带噪信号和对应的纯净信号之后,按照图1所示特征提取流程完成数据集的构建,分帧后每帧信号的长度为4 224点,帧移步长为信号长度的一半。需要说明的是,DnCNN网络模型的输入尺寸中,频率维度的尺寸是由STFT变换决定的,模型的输入尺寸不宜过大也不宜过小,因而STFT变换中的点数设置为128点,用单边谱表示其变换结果时,频率维度的尺寸即为65,时间维度的尺寸与频率维度保持一致,所以DnCNN的输入尺寸取为65×65。时间维度的65意味着进行STFT变换的每一帧信号需要再次分为65帧并进行加窗,为了使STFT时信号的恢复更加平滑、避免出现畸变,在这里窗函数选择128点的正弦窗,帧移步长为窗函数长度的一半,则原分帧信号的长度即为4 224点,声信号的采样频率为35.28 kHz,这也就说明DnCNN感受野的时间长度约为0.12 s,模型特征学习和结果预测都是基于0.12 s内信号中蕴含的信息。带噪信号和纯净信号经过特征提取后,共计生成了60 756对训练样本,按照8∶2的比例将训练样本划分为训练集和验证集。

3.3 训练参数设置

DnCNN模型的训练在GPU服务器上借助MATLAB R2022b深度学习框架进行,服务器CPU为Intel I9 12900KF,内存64 GB,GPU为RTX3090Ti,显存24 GB。小批量处理大小设定为64,初始学习率设置为0.001,训练轮次共50轮,学习率衰减因子为0.85,即每轮次训练开始时学习率衰减为上一轮次的0.85。梯度下降方法选择Adam,每轮次训练开始时均进行训练集样本顺序打乱操作。经过约6.8 h的训练后,模型收敛,完成最大训练轮次,训练完成。

3.4 结果分析

为了对空化声信号增强方法的增强效果进行检验,从得到的纯净信号和噪声信号中各截取出长约10 s未参与训练数据集构建的信号,按照不同的信噪比进行混合,生成用于检验的带噪信号。检验过程即按图1中增强阶段的流程进行,采用信号处理领域常用的客观评价指标对该方法的增强效果进行客观评价,如信噪比(signal to noise ratio,SNR),峰值信噪比(peak signal to noise ratio,PSNR),均方误差(mean square error,MSE),指标计算公式为

(13)

(14)

(15)

(16)

式中：y为纯净的空化声信号;y1为带噪空化声信号;y0为经过增强后的空化声信号;N为信号长度;RSNIN为输入信噪比;RSNOUT为输出信噪比,信噪比越高,数据质量越好,则说明该方法声音增强效果越好;EMS为均方误差,表示经过声音增强后的带噪空化声信号与纯净的空化声信号的差异程度,即残余泄流噪声信号的平均能量,EMS越小,说明信号能量相差越小;RPSN为峰值信噪比,表示纯净信号的峰值能量与噪声的平均能量的比值;RPSN越大说明增强后的信号越接近原始信号。

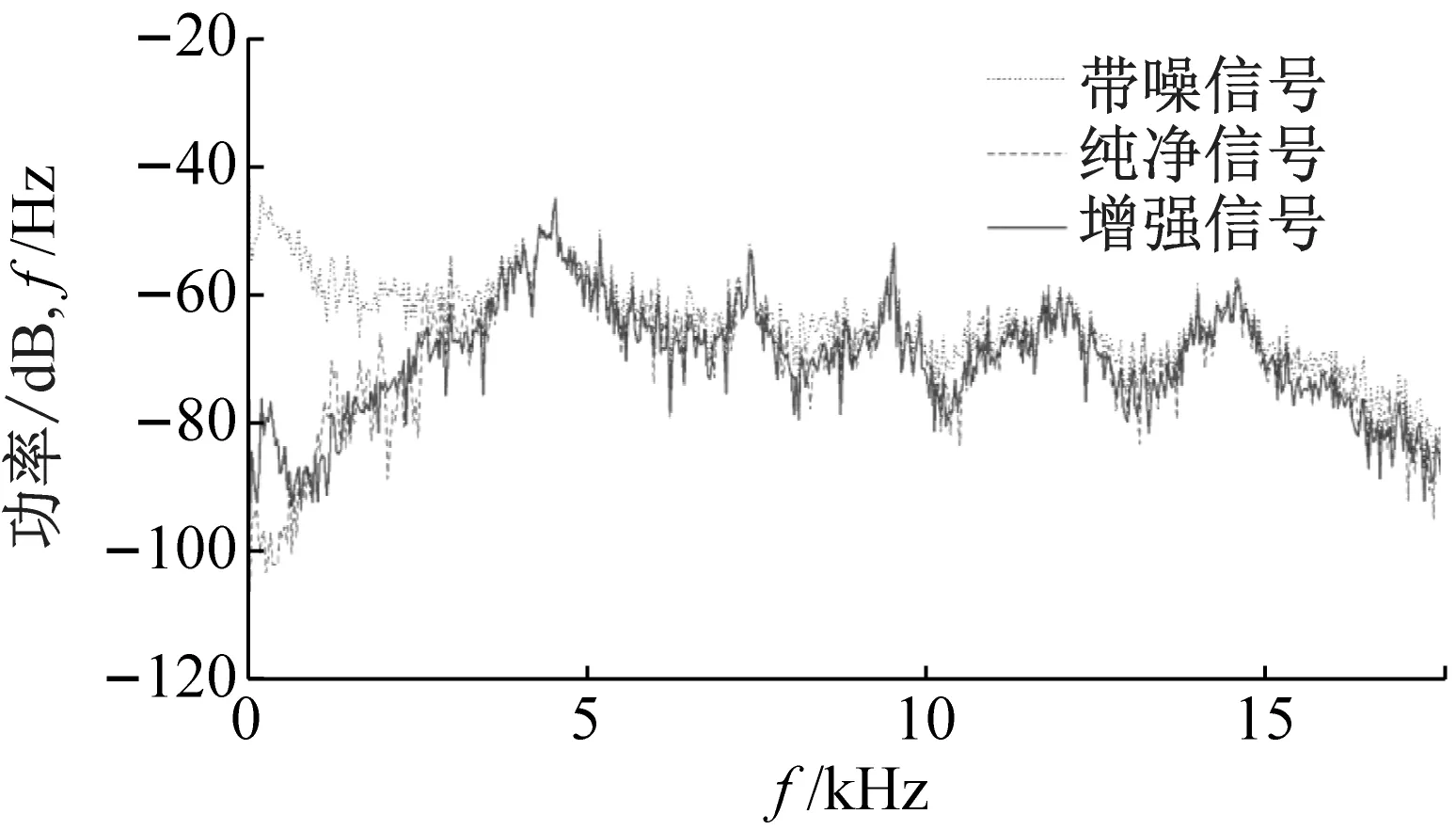
当输入信噪比RSNIN分别为-5 dB,-10 dB,-15 dB,-20 dB时,带噪空化声信号增强前后的时频图如图8所示。由图8(a)～图8(d)可知,随着输入信噪比的不断降低,空化声信号的能量在整个频域内逐渐被泄流噪声的能量所掩盖,空化声信号与泄流噪声在中低频段的频带重叠问题也愈发明显。可以预见,在这类情境下应用小波变换等传统方法对空化声信号进行去噪,在设定阈值、小波函数等参数[24-25]时会存在较大的主观随意性,去噪效果难以保证。由图8(e)～图8(h)可知,在不同的输入信噪比条件下,应用本文提出的空化声信号增强方法后,均得到了较为明显的增强效果,无需再设定任何参数,也没有再引入其他假定条件。图8所示4种输入信噪比下的带噪空化声信号增强前后与纯净空化声信号的功率谱密度对比图,如图9所示。

(a) RSNIN=-5 dB增强前

(a) RSNIN=-5 dB

由图9可知,随着输入信噪比的不断降低,带噪信号逐渐丢失了纯净信号的频谱特征,当输入信噪比为-15 dB,-20 dB时空化声信号的能量几乎完全被泄流噪声的能量所掩盖,但是经过增强后的信号仍然还原出了纯净信号的频谱结构特点,获得了高度的相似性,增强信号与纯净信号在频域的变化趋势上保持了一致。此外也发现,在噪声能量明显高于空化声信号能量的频段内,信号的增强效果并不十分理想,只还原出了整体的频谱结构特征,未能准确地还原出频段内能量峰值等细部频谱结构特点,说明该方法仍有待进一步改进的空间。图9所示的结果总体表明该方法能够较好的还原出目标信号的频谱结构特点,这对于目标信号的识别和后续的研究处理等是十分重要的。

经过声音增强后,增强信号的输出信噪比RSNOUT、峰值信噪比RPSN和均方误差EMS随输入信噪比变化的过程如表1所示。由表1可知：在多种低输入信噪比条件下,带噪空化声信号经过增强后,输出信噪比较输入都有了较大的提升,输入信噪比越高,增强后信号的输出信噪比也越高,但是输入信噪比越低,信噪比的提升越明显;在不同的输入信噪比条件下,峰值信噪比均保持在了较高的水平,说明声音增强后信号的峰值能量与原信号极为接近,侧面反映了以对数功率谱为特征输入的DnCNN网络模型对于信号中的能量特征具有较强的学习能力;均方误差随着输入信噪比的提升也有所改善,但是并不明显,始终处于较小的范围内。综上所述,即使在构建DnCNN网络模型的训练集时,仅选择了-5 dB,-10 dB,-15 dB,-20 dB作为带噪信号的输入信噪比,但是检验结果表明,该方法对于多种低信噪比条件下的空化声信号都取得了较好的增强效果,说明基于DnCNN声音增强的空化声信号增强方法具有较好的鲁棒性。

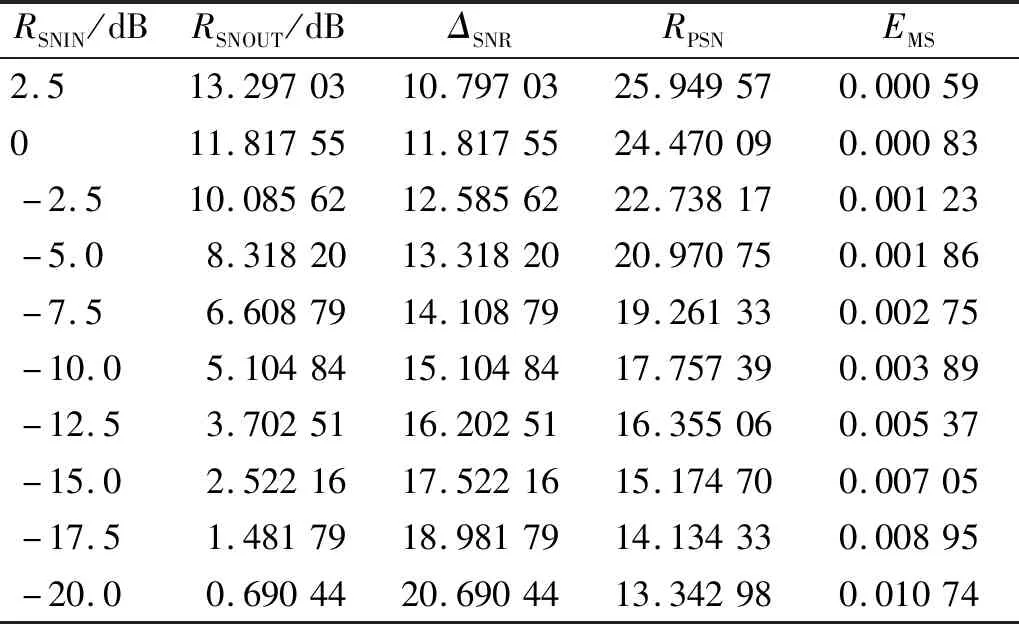
表1 增强信号评价指标计算结果汇总

此外,在相同检验信号的基础上,选择了信号处理领域常用的小波(Wavelet)去噪、经验模态分解(empirical mode decomposition,EMD)去噪以及分别基于最小均方误差(least mean square,LMS)和递推最小二乘法(recursive least square,RLS)的自适应滤波器等4种方法与本文提出的基于DnCNN声音增强的空化声信号增强方法进行对比,评价对比结果如表2所示。其中小波去噪方法小波分解级别设为15,去噪方法选择经验贝叶斯,分别选择sym4小波、软硬阈值折中函数作为小波基和阈值函数。EMD去噪方法选择分段3次Hermite插值方法作为包络线构造的插值方法,只保留前两个IMF(intrinsic mode function)分量用于去噪信号的重构。基于LMS和RLS的自适应滤波方法中参考信号均节选自前述用于构建训练集的空化声信号。从评价对比结果来看,小波去噪方法几乎没有对输出信号的质量带来有效的提升,信号的输出信噪比与输入信噪比基本相同。EMD去噪方法在-5 dB,-10 dB的输入信噪比条件下取得了相对较好的结果,但在-15 dB,-20 dB相对更低的信噪比条件下表现不佳。基于LMS和RLS的自适应滤波方法虽然在4种不同的输入信噪比条件下都取得了一定的增强效果,但与本文方法相比仍然存在着较大的差距,仅在-20 dB的输入信噪比条件下,二者结果较为接近。可见在低信噪比应用场景下,本文方法与传统方法相比有着较大的优势。

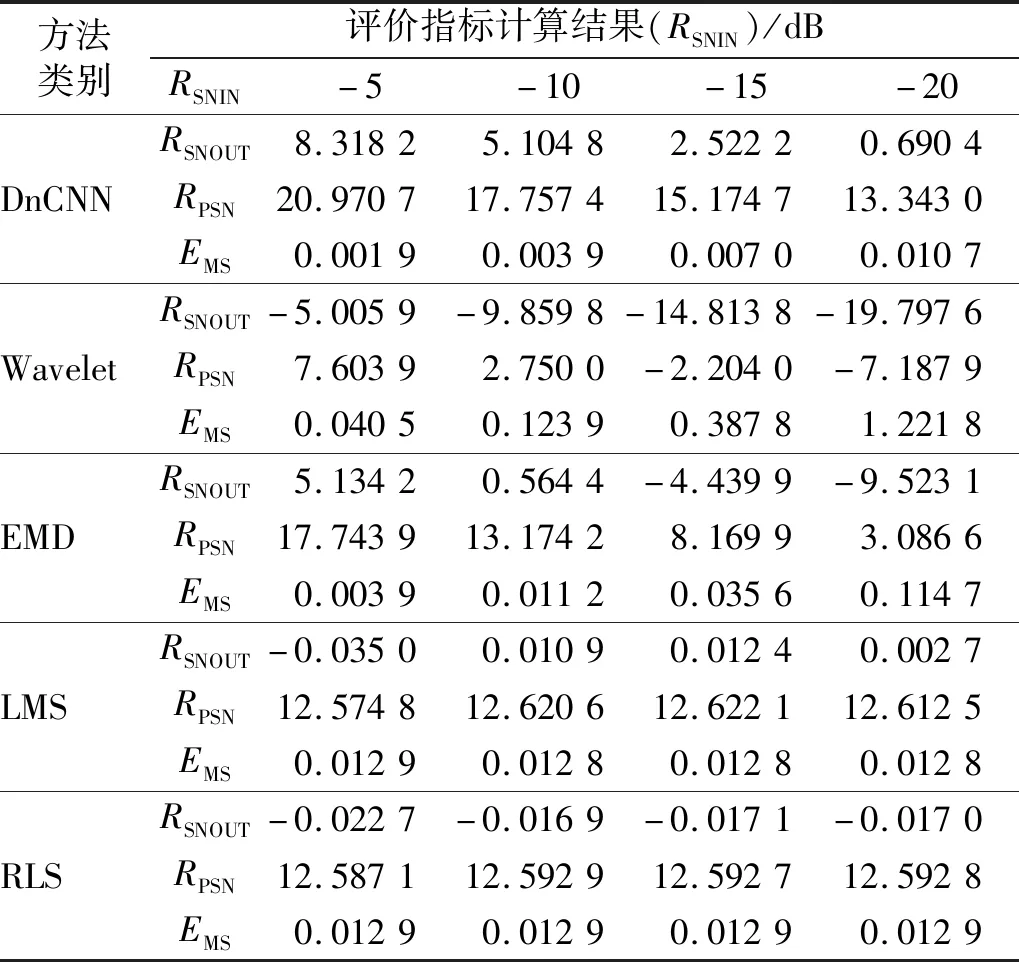
表2 不同方法信号增强效果对比

4 工程应用

4.1 试验一：目标信号多分类识别试验

为了进一步地证明该增强方法的泛化性能,并且对其工程应用价值加以验证,本文设计了不同种类音频监测信号的识别试验,用以模拟实际工程中应用音频监测方法进行水工建筑物泄洪安全监测的情况。选用支持向量机(support vector machine,SVM)作为音频监测信号的识别分类模型,通过考察支持向量机对增强前后的带噪信号识别分类准确率的变化,对该增强方法的性能进行评价。

应用该增强方法首先仍然需要完成DnCNN网络模型的训练,数据集的构建过程与3.2节构建过程完全一致,仅对信号样本的种类进行了扩充,在空化声信号的基础上又补充了泄洪警报、异常啸叫和泄流噪声3种声信号。泄洪警报是水利枢纽开闸泄洪前的预警警报声,异常啸叫是由高速水流激发的异常声信号,采集自某水利枢纽泄洪现场,空化声信号、泄洪警报和异常啸叫均表征水工建筑物泄流过程中有异常状况发生的情况,泄流噪声取自3.1节泄流试验采集信号,作为纯净信号时用于表征泄流过程中无异常状况发生的情况。4类信号样本均进行了滤波和重采样处理,重采样频率为35.28 kHz,长度相同,与3.2节数据集构建过程一致,4类信号样本需要分别与3.2节试验中使用的3段泄流噪声信号按照-5 dB,-10dB,-15dB,-20 dB的输入信噪比进行混合,生成带噪信号用于数据集的构建。最终生成了约24万对训练样本,同样按照8∶2的比例划分为训练集和验证集。

训练过程中参数的设置同3.3节,经过约26 h的训练后,模型收敛,完成最大训练轮次,训练完成。同样选取未参与数据集构建的信号构成4类测试信号,测试信号的长度相同,按照图1中增强阶段的流程进行增强,测试信号经增强后的输出信噪比、峰值信噪比和均方误差计算结果如表3所示。

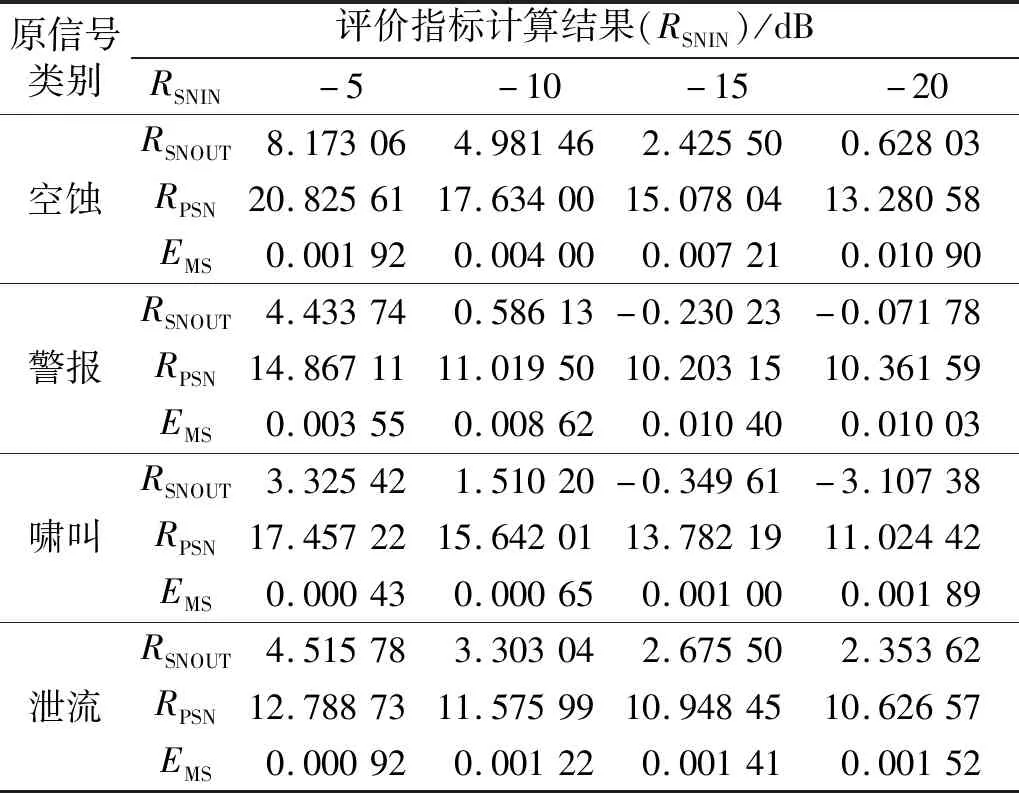
表3 4类增强测试信号评价指标计算结果汇总

由表3可知,该增强方法不仅对空化声信号有着较好的增强效果,对其他种类声信号的增强效果也较为明显,说明该方法有着很强的泛化能力,使用一定数量不同类别的训练样本完成训练后,对于不同类别的声信号DnCNN网络模型能够获得较强的识别能力。

完成声信号增强过程之后,最终可以得到纯净信号以及不同输入信噪比条件下的带噪信号和增强信号。对纯净信号进行分帧处理,帧长为0.1 s,每帧信号均作为一个样本,依次计算峭度、重心频率、卓越频率、功率谱熵等多种时域、频域和信息熵指标,将计算结果作为样本的特征值,由此构建训练集用于SVM的训练。训练集构建完成后对不同输入信噪比的带噪信号和增强信号进行同样的操作,构建测试集。在训练过程中,选择高斯径向基核作为SVM的核函数,惩罚参数C和径向基核参数γ经过网格寻优后分别确定为0.088 4和0.176 8,训练后的SVM模型最终在训练集上获得了100%的识别分类准确率。

增强前后的带噪信号构成的测试集在SVM模型上的识别分类准确率,如图10所示。由图10可知,带噪信号构建的测试集样本相较于纯净信号构建的训练集样本,在识别分类准确率上有较大的下降,这表明在低信噪比条件下泄流噪声能够大幅削减泄洪安全音频监测方法的效果,甚至致其完全失效。而经过增强后,增强信号构建的测试集样本在分类模型上获得的识别准确率相较于增强前均有了较大的提升,提升效果明显,即使在-20 dB极低的信噪比条件下,仍然保持了近60%的识别准确率,这表明本文提出的基于DnCNN声音增强的空化声信号增强方法不仅适用于低信噪比条件下空化声信号的增强,应用于其他种类的声信号时也能够表现出不错的增强效果,具有较强的泛化能力。

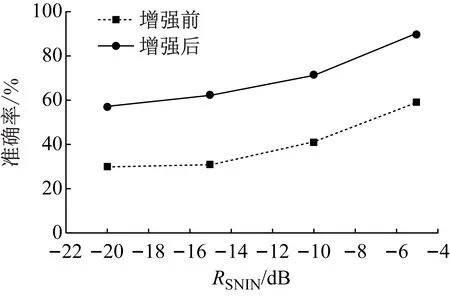
图10 带噪信号增强前后SVM识别准确率

4.2 试验二：空化声信号单分类识别试验

在实际的工程应用场景下,泄流过程中声信号的监测采集和识别分类不会只受到泄流噪声一类背景噪声的影响：通气孔、泄洪洞等部位由于风速、流速过大而引发的各种异响,闸门起落、坝体维护施工以及坝顶道路过往工程车辆发出的噪声等等,均可能成为影响泄洪安全音频监测方法效果的背景噪声。所以,本文方法在不同种类背景噪声条件下的性能表现是必须考虑的问题。此外,各种背景噪声出现的时间点、持续时长不一,导致不同种类的背景噪声混杂叠加在一起,这对本文方法的应用来说也是极大的考验。为探明本文提出的基于DnCNN声音增强的空化声信号增强方法在不同种类背景噪声下的性能表现,基于信号识别分类试验中的试验数据,并结合单分类支持向量机(one-class support vector machine,OCSVM)[26]进行空化声信号单分类识别试验。从DnCNN模型训练到使用OCSVM对方法的性能表现进行评价,试验策略与试验一大体一致,仅在目标纯净信号和背景噪声信号的选择以及评价方法上存在不同。

DnCNN网络模型的训练数据主要基于试验一使用的4类纯净信号,仅保留空化声信号作为该试验的目标纯净信号,其余3类纯净信号均作为背景噪声信号。为进一步丰富背景噪声的种类,将一段采集自公路的车辆来往噪声也作为试验中的一类背景噪声,同时可用以表征实际声信号采集过程中坝顶道路往来工程车辆的情况。考虑到不同种类背景噪声的混杂叠加以及实际声信号采集过程中泄流噪声会是背景噪声的主要来源,所以将泄流噪声与其余3类背景噪声均按照1∶1的能量比进行叠加,将生成的3类叠加噪声信号也作为该试验的背景噪声。试验一、试验二目标纯净信号与背景噪声信号组合的对比,如表4所示。从试验二的7类背景噪声和1类目标信号中各截取出长约10 s的测试信号后,将7种信号组合同样按照-5 dB,-10 dB,-15 dB,-20 dB的输入信噪比进行混合,用以构建数据集,最终生成了近14万对训练样本,按8∶2的比例划分训练集和验证集。训练参数设置仍与3.3节保持一致,经过约13 h的训练后,DnCNN模型训练完成。将截取出的测试空化声信号和背景噪声以相同的信号组合和输入信噪比进行混合生成带噪信号,并应用本文方法将带噪信号输入DnCNN模型进行增强,最终可得到纯净的空化声信号以及4类输入信噪比条件下含不同种类背景噪声的带噪空化声信号和对应的增强信号,从而可结合OCSVM进行下一步的试验。

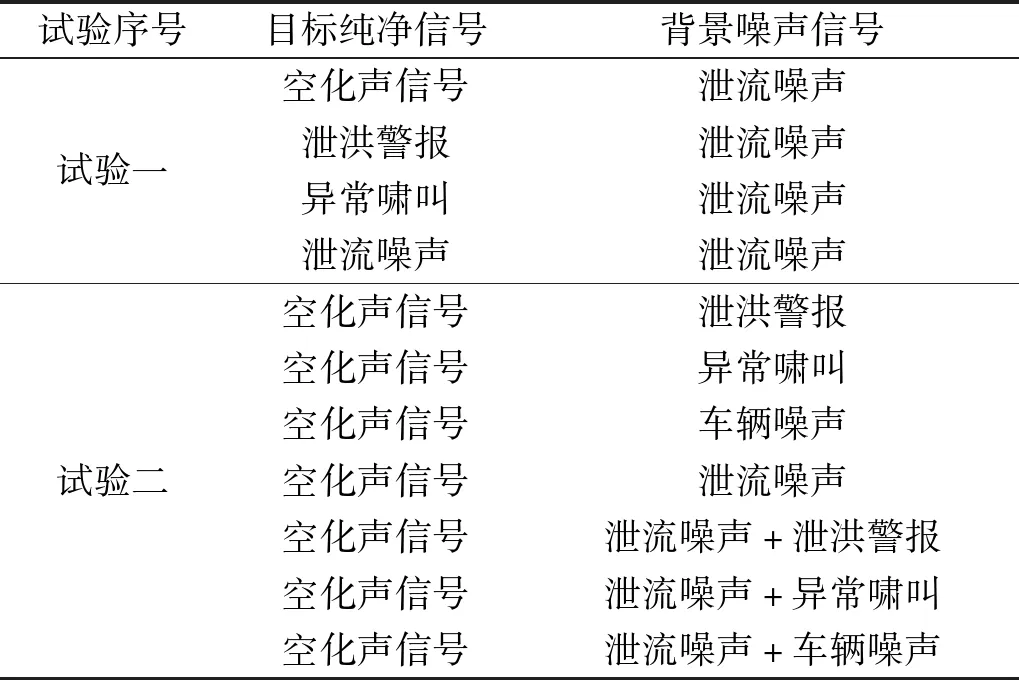
表4 试验一与试验二信号组合对比

OCSVM的训练数据仅有一类,其基本原理是通过核函数将训练数据映射进特征空间,在特征空间内求解一超平面将原点与训练数据样本点分离,并使得原点与超平面之间的距离最大化,当测试数据样本点在特征空间内落入训练数据样本点所在的区域时,即认为测试数据与训练数据属同一类,反之则不属于同一类。由此可见,单分类支持向量机属特殊类型的SVM,使用方法也与其类似：以正确识别空化声信号样本为目标,首先使用纯净空化声信号构建训练集用于OCSVM模型的训练,构建方式同试验一中SVM模型训练集的构建方式,但得到的训练集中仅有一类数据。模型训练完成后,以同样的方式分别使用带噪空化声信号和其对应的增强信号构建测试集,通过对比模型在两个测试集上的识别正确率,即可对本文方法在不同种类背景噪声下的性能表现进行评价。在OCSVM模型的训练过程中发现,对样本数据应用主成分分析(principal component analysis,PCA)方法进行降维后,模型可以得到更好的性能,遂对训练集和测试集中的样本数据均应用相同的PCA方法将样本数据降至4维。仍然选择高斯径向基核作为核函数,径向基核参数γ和离群值上限参数ν经过网格寻优后分别确定为0.025 4和0.002 6,最终得到的OCSVM模型在训练集上获得了97.40%的识别正确率。

增强前后的带噪空化声信号构成的测试集在OCSVM模型上的识别正确率,如图11所示。由图11可知,OCSVM方法对于样本数据的变化较为敏感,添加了不同种类的背景噪声后,模型基本已无法从样本数据中识别出空化声信号的存在。而同样的带噪信号经过了本文方法进行增强后,构成的训练集在OCSVM模型上的识别正确率有了显著的提升,在-5 dB的输入信噪比条件下达到了90%的正确率,已相当接近训练集样本97.40%的正确率,由此说明本文提出的基于DnCNN声音增强的空化声信号增强方法能够实现对各类背景噪声的有效去除、极大地还原空化声信号的频谱结构特征,也证明了该方法在不同种类的背景噪声条件下均能获得良好的性能表现,具有较好的实用性和工程应用价值。

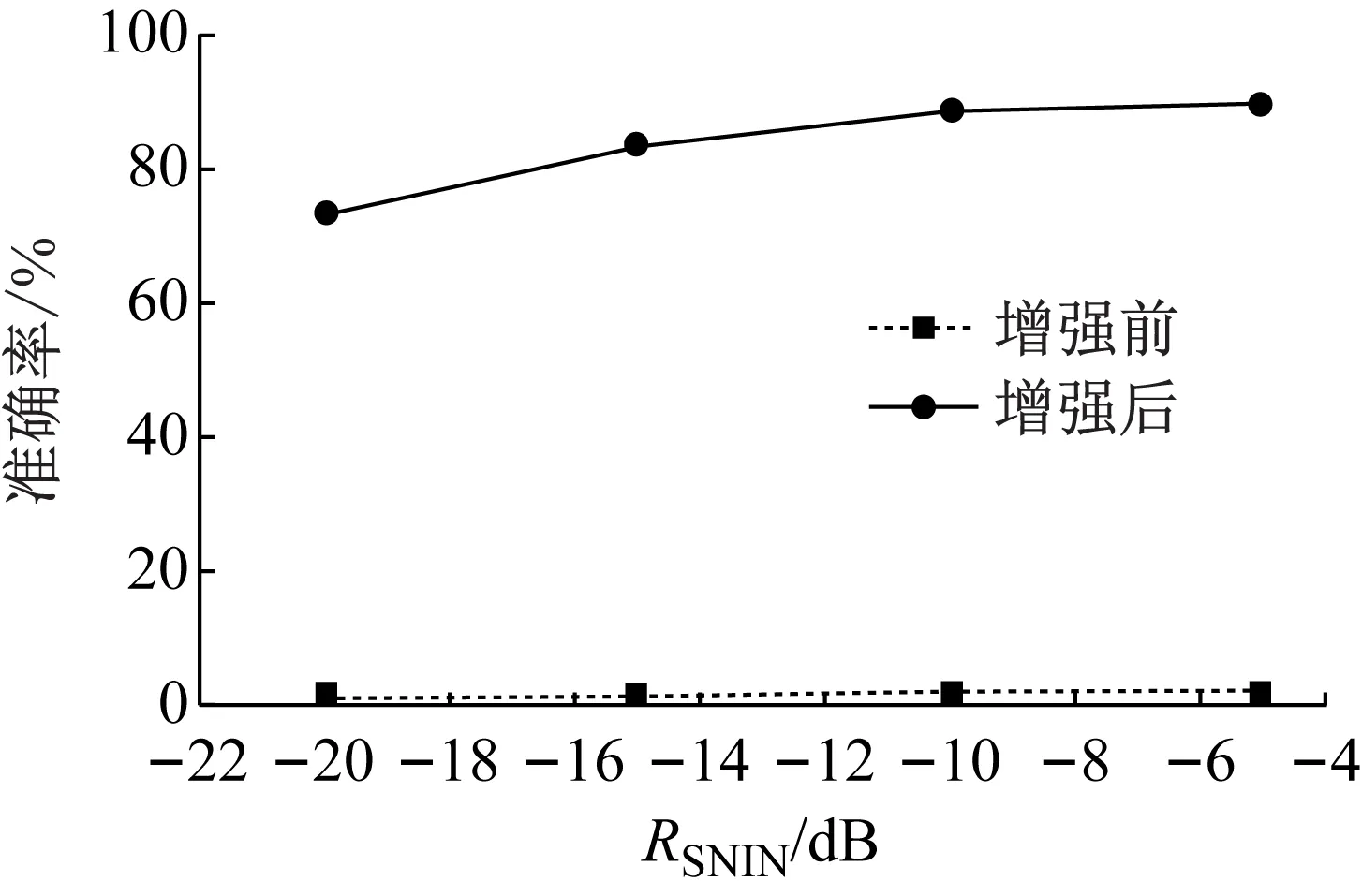
图11 带噪空化声信号增强前后OCSVM识别正确率

5 结 论

空蚀空化是威胁水工建筑物汛期泄洪安全的重要因素,声测法是监测空蚀空化现象的重要手段,然而汛期强泄流噪声能够致使声测法效果大幅衰减甚至完全失效,对水工建筑物的安全稳定运行产生潜在威胁。为解决该问题,本文基于语音增强思想和DnCNN网络模型,提出了基于DnCNN声音增强的空化声信号增强方法,对于强泄流噪声影响下的微弱空化声信号,应用该方法能够有效地对其进行增强,提升音频监测信号的信噪比,并高度还原空化声信号的频谱结构特点。该方法具有较强的鲁棒性,经过试验验证,在不同的低信噪比条件下,该方法对于带噪空化声信号均能够获得良好的增强效果。同时,该方法也能够有效增强其他种类的目标声信号、消除不同类别的背景噪声,具有较好的泛化能力和工程实用性。研究结果表明,该方法在水工建筑物泄洪安全监测领域有着巨大的发展潜力和广阔的应用前景。但是本文所作工作仍有待完善之处,试验所用空化声信号采集自振动空蚀试验,与实际水工建筑物流道内的空化声信号相比存在着一定的差异,进一步的研究应通过原型监测等手段采集实际工程中的空化声信号,据此对DnCNN网络模型的参数进行调整,提升其工程实用性。