微型多叶稀薄气体润滑动压轴承动态特性研究
2023-11-14郗文君毕春晓张彩丽曹巨江
吴 垚,郗文君,毕春晓,张彩丽,曹巨江
(1.陕西科技大学 机电工程学院,西安 710021;2.施耐德(西安)创新技术有限公司 低压事业部,西安 710075;3.沈阳大学 机械工程学院,沈阳 110044)
近年来随着超精密加工技术的不断革新,航空航天、国防军工、电力能源和低温制冷等领域的机械设备向着微型化、高精度、多功能、低功耗以及智能化等方向快速发展。使微型涡轮发动机、微型燃气轮机和微型涡轮增压器等微型透平旋转机械实现了各种能量转换、效率提升和微动力输出[1-2]。由于微型涡轮发动机工作条件严苛,滚动轴承很难承受极端高速高温环境,磁悬浮轴承易受到外界电磁干扰以及静压气体轴承需附加额外供气装置,而微型动压气体滑动轴承具有结构简单、回转精度高、与微加工技术兼容、气体介质性能稳定、无污染、摩擦功率损耗小以及工作温度范围宽等优点,能够支承微型转子高速稳定运转[3-4]。
相比360°圆轴承结构最简单但高速下易出现自激涡动失稳。动力稳定性和自对中性更好的可倾瓦轴承以及弹性箔片轴承则结构复杂、装配要求高且易形成误差累积,很难实现微小空间内的超精密加工。多叶动压气体轴承的瓦间沟槽具有防止压力扰动扩散、削弱气膜交叉刚度和收集杂质粒子的作用,各周向槽视作一个“气泵”会增加润滑膜厚和质量流量,减小轴颈-轴瓦表面的接触概率[5]。另外,如果转子直径在毫米数量级,轴颈和轴瓦间的润滑膜厚与气体分子平均自由程相比不可忽略,需要对微型气体轴承性能进行更加精确的预测,必须考虑气体稀薄效应的影响。综上所述,微型多叶气体轴承可满足微纳米尺度加工工艺和微型轴承-转子系统超高速高温工况下运行可靠性。
自从Lund等[6-7]首先基于Reynolds方程的等效变分和小扰动法得到滑动轴承的8个刚度和阻尼系数,使得分析轴承-转子系统动力学行为成为可能。国内外学者针对动压滑动轴承的动态特性开展了大量理论和试验研究,取得了许多重要进展。Zirkelback等[8]根据窄沟槽理论和有限元法,确定了使人字形槽轴承直接刚度和临界质量最大的几何结构参数。为提高箔片轴承的承载力,张广辉等[9]提出一种带弹簧支撑结构的油润滑多叶箔片轴承,分析了动态系数随转速、载荷和Sommerfeld系数的变化规律。方华等[10]研究了气体动力黏度、波箔片弹性模量和泊松比对Hydresil型波箔动压气体轴承动特性的影响,指出动态刚度系数随黏度和弹性模量的增加而增大,泊松比对动态系数影响较小。Bompos等[11]通过磁场强度定义磁流变液体和纳米磁流变流体的表观黏度,对比了牛顿流体、磁流变流体和纳米磁流变流体润滑剂对滑动轴承动态性能的影响。尹明虎等[12]利用出口质量守恒边界条件和CFD(computational fluid dynamics)动网格技术建立了微织构滑动轴承动态特性有限元分析模型,发现微织构形状、尺寸和分布参数对阻尼系数影响更显著。李强等[13-14]基于自编FLUENT-UDF程序开发了适用于多油楔滑动轴承结构的动网格方法,可实现轴颈任意扰动下动态特性的瞬态计算。胡小强等[15]提出了一种3层箔片叠加的叠片式箔片动压气体推力轴承结构刚度模型。Wang等[16]结合影响系数法和谐波激励法计算了人字形槽和圆柱气体轴承的动态系数,借助动网格技术对卷吸边界实现双向流固耦合模拟,比较了两种动压轴承-转子系统的稳定性。本文作者[17]引入一阶、二阶滑移模型、Fukui-Kaneko和Boltzmann稀薄效应模型,推导了微型动压气体轴承动态修正Reynold方程,研究了Knudsen数、稀薄效应模型和轴承参数对动态系数的影响规律。燕震雷等[18]也对比了连续模型、一阶滑移模型和Wu新滑移模型速度边界对三可倾瓦动压轴承各瓦块气膜压力和承载能力的影响。于海洋[19]建立了计入气穴效应、转轴/轴瓦综合弹性变形和热效应的复合织构化滑动轴承动态特性分析模型,说明气穴和润滑剂黏温热效应会降低轴承动态系数及系统临界失稳转速。Bi等[20-21]考虑超临界二氧化碳(supercritical carbon dioxide,S-CO2)的可变热力学特性、湍流效应及真实气体效应,推导了二维绝热S-CO2可倾瓦轴承的能量方程,通过包含完全变量的偏导数法研究了S-CO2轴承的热流体动压润滑机理。Roy等[22]利用Monte Carlo模拟量化了表面粗糙度和偏心率的随机性对双轴向槽动压轴承静动态性能的影响。Singh等[23]采用伽辽金有限元法分别求解光滑、完全和部分球形织构表面双叶/圆柱滑动轴承的Reynolds方程,发现表面织构提高了润滑膜的直接阻尼系数、轴颈临界质量和失稳转速。赵琪等[24]通过能量耗散方法分析了顶箔-波箔-轴承座间的库伦摩擦力对波箔气体轴承动态系数的影响,指出轴承刚度随摩擦因数的增加而增加,但库仑阻尼功耗会下降。Sharma等[25]讨论了偏心率、偏置量和微极性参数对非圆偏置轴承刚度和稳定性的影响。
微型涡轮发动机的高速稳定性取决于其支承轴承超薄气膜刚度和阻尼系数的综合作用。目前在微型动压气体轴承润滑性能的研究中,轴承结构主要是360°圆轴承,轴颈-轴瓦微纳尺度间隙内薄膜形成及润滑机理尚不明确,有关微型多叶气体轴承动态特性的理论模型还需深入研究。本文综合考虑膜厚、压力及Poiseuille流量比频率扰动的偏导数法,给出适用于微型多叶稀薄气体动压润滑轴承的频变动态特性计算方法,为微型涡轮发动机性能预测及优化设计提供理论基础和技术支撑。
1 微型三叶动压气体轴承结构
微型多叶动压气体轴承一般由多块圆弧轴瓦组成,各瓦块沿圆周方向均匀分布,常见的是三叶和四叶气体微轴承。瓦上和瓦间支承方式的三叶微气体轴承结构图和模型图,如图1、图2所示。依靠轴颈/轴瓦间超薄气膜实现微转子无接触悬浮,ε和θ为任意时刻的轴颈偏心率和偏位角,ε0和θ0为轴颈静平衡位置的偏心率和偏位角,φ为从y轴负方向逆时针开始计算的气膜位置角,R为轴颈半径,h为超薄气膜厚度,ω为轴颈转动角速度,α为轴瓦包角,ξ为瓦间槽宽包角,γ为轴承上方竖直线到第一块瓦进气边的位置角,微型多叶动压气体轴承相比360°圆轴承的结构特点是具有两个间隙,一个是半径间隙Cb,即轴瓦内圆弧半径与轴颈半径之差,另一个是装配间隙Cp,即轴瓦支点圆与轴颈半径之差。

(a) 瓦上承载
2 超薄气膜润滑基本方程
1.1 气体稀薄效应修正模型
微型转子高速旋转带动稀薄气体,在微型多叶轴承表面形成超薄润滑气膜为转子提供支承。忽略润滑膜的惯性效应和热效应且假设稀薄气流为层流,采用Boltzmann方程考虑气体稀薄效应的超薄气膜润滑无量纲修正Reynolds方程为
(1)

为提高稀薄气体润滑修正Reynolds方程的计算准确性,Hwang等[26]在高阶滑移模型中引入包含3个可调系数的附加修正项,推导了Boltzmann修正模型的速度分布表达式
(2)
式中:a为表面修正系数,a1,b1和c1为3个可调系数,a1=0.018 07,b1=1.353 55和c1=-1.174 68;D为逆Knudsen数,D=π/2Kn,Knudsen数Kn=λ0/h,λ0=65 nm为气体平均分子自由程。
式(2)中u的第二项给出了压力流的速度分布,无量纲Poiseuille流量系数QP-Boltzmann为

(3)
将式(3)中Boltzmann稀薄效应修正模型与连续流流量系数Qcon相比得到Poiseuille流量比Q为
(4)
式中,Qcon=D/6。
将Q变换成Knudsen数的表达式[27]
(5)
1.2 轴颈小扰动时微型多叶轴承的动态系数
任意时刻绕其静态平衡点的动态小扰动轴颈位置可由偏心率ε和偏位角θ确定,设轴颈静平衡位置为(ε0,θ0),轴颈绕静态平衡点的动态周期性小扰动记为E和Θ,则轴颈小扰动情况下轴颈位置[28]为

(6)
式中:Ed和Θd为定义在复数范围内的扰动偏心率和扰动偏位角幅值;Ω为无量纲扰动频率;i为虚数单位。
相应的动态气膜压力和气膜厚度表示为
(7)
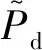
值得注意的是,稀薄效应修正系数Q是与气膜厚度有关的变量,因此,轴颈小扰动下Q也具有如下形式
(8)


(9)
其中,

(10)
将式(7)和式(8)代入式(1),并利用静态修正Reynolds方程和略去高阶项进行化简,得到稀薄气体润滑动态修正Reynolds方程为
(11)
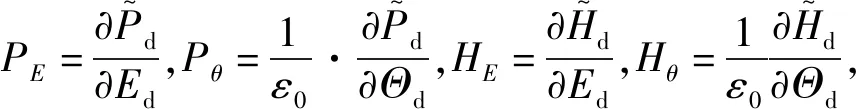
相应的边界条件为

(12)
式中:B为轴承宽度;φ0为从角起线到轴瓦进气边的角度;φ1为从角起线到轴瓦出气边的角度。
轴颈小扰动下轴瓦无量纲动态刚度和阻尼系数可按下式计算

(13)
式中:ε和θ分别为轴颈静态平衡位置对应的偏心方向和偏位角方向;Kij(Dij)为由j方向无量纲单位位移扰动(速度扰动)在i方向所产生的无量纲气膜力(i=x,y;j=ε,θ)。
通过转换矩阵A得到图1所示的直角坐标系中8个动态系数
(14)
因此,整个微型三叶动压气体轴承的动态刚度和阻尼系数为
(15)
1.3 动态修正Reynolds方程的有限差分解法
稀薄气体润滑动态修正Reynolds方程是二维非线性偏微分方程,为了快速数值求解,将式(11)进一步进行整理为
(16)
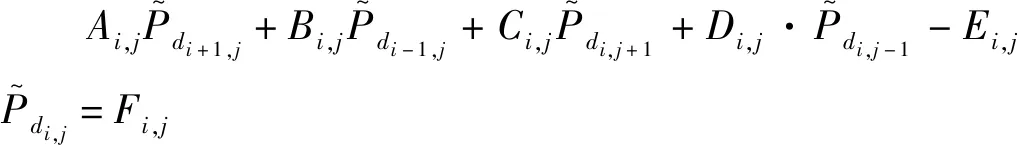
(17)


(18)
(19)
(20)
2 结果与讨论
文中分别对微型气体360°圆轴承和多叶轴承动态特性结果进行了对比和分析,选取微型三叶动压气体轴承的结构参数如下:轴承半径间隙Cb=1 μm,瓦块包角α=3×100°,瓦上承载和瓦间承载的第一块瓦进气边位置角η分别为-10°和50°,气体动力黏度为1.8×10-5Pa·s,环境压力pa=1.013×105Pa。阐明了扰动频率、偏心率、轴颈转速、长径比和瓦块分布位置对动态刚度和阻尼系数的影响规律。
为验证微型多叶稀薄气体润滑微轴承动态性能计算方法和自编程序的可靠性,表1对比了本文与文献[30]有关轴向槽气体轴承无量纲动态系数的直接项,虞烈等采用了MATLAB PDE工具箱求解气体润滑Reynolds方程,为了充分检验作者提出的方法,选取了4种轴向槽轴承结构进行比较,由表1可知,两者的数值结果吻合较好,其误差均在3.5%以内,说明了算法和程序的准确性。
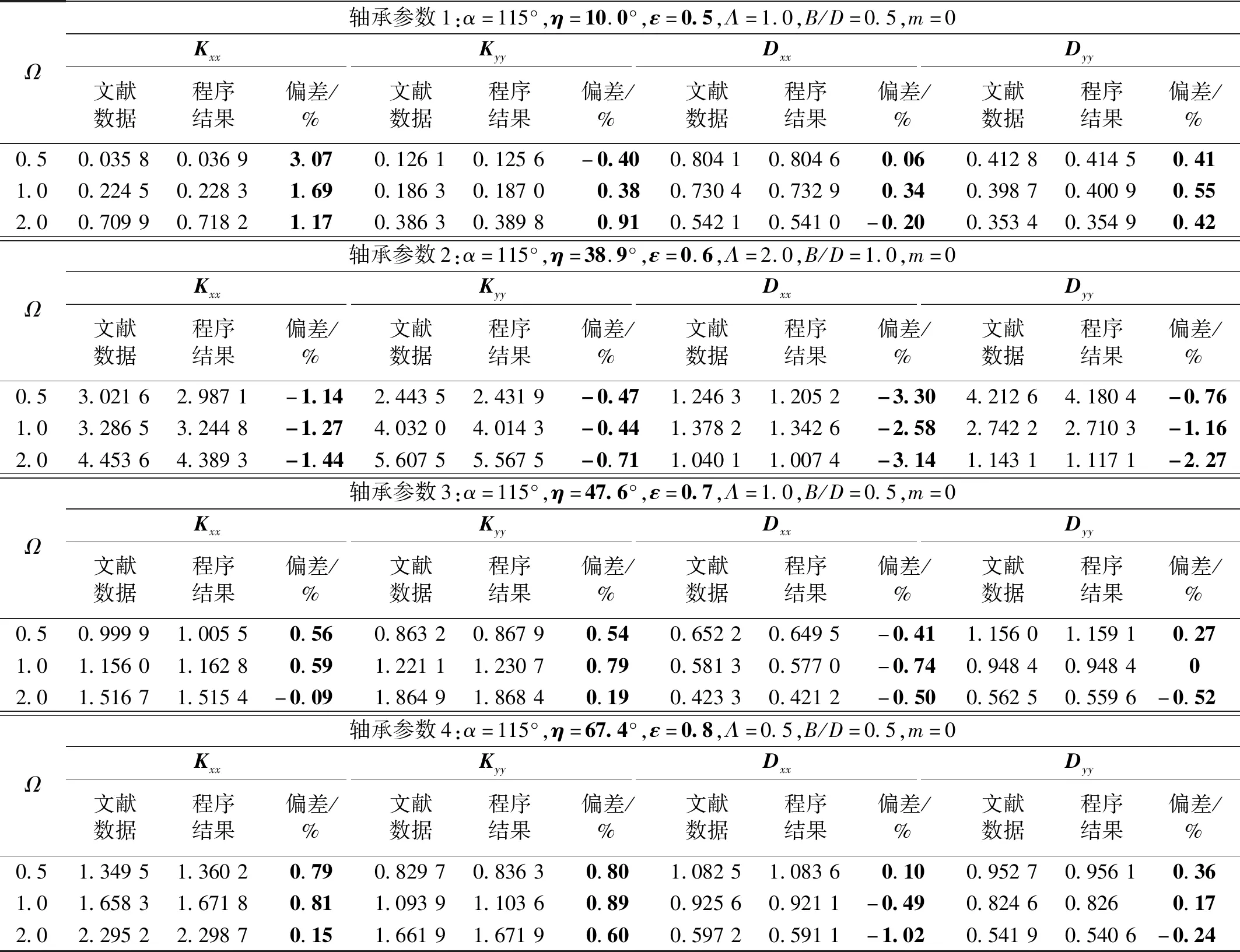
表1 文中方法与文献[30]的动态系数结果对比
当ε=0.7,B/D=0.1,Λ=15时微型多叶气体轴承和360°圆轴承的动态刚度和阻尼系数随轴颈扰动频率的变化曲线,如图3、图4所示。由图3、图4可知,两种结构轴承的Kxx和Kyy均随扰动频率的增加而增大且x方向的直接刚度系数略大。增加轴瓦预负荷也会提高轴承的直接刚度系数,预负荷系数越大,Kxx和Kyy的增加幅度越明显,预负荷系数的变大降低了轴颈与轴瓦的润滑间隙,有效提高了超薄气膜刚度。值得注意的是,瓦间承载的气膜直接刚度系数大于瓦上承载方式,这与常规尺度轴向槽气体轴承结果相反,这是因为多叶轴承瓦间沟槽的“泵吸效应”,吸入的外部气体提高了润滑剂流量,降低了气体稀薄程度,且当预负荷系数较大时,微型多叶轴承的Kxx和Kyy大于相同结构参数的360°圆轴承,说明合适的预负荷系数可增强超薄气膜支承刚度,弥补了气膜不连续带来的影响。交叉刚度系数的变化规律相对复杂,瓦间承载微型多叶轴承的Kxy和Kyx随Ω的增加先快速增大,扰动频率大于3.5交叉刚度系数趋近于稳定值。当Ω>1.5时,瓦上承载方式下交叉刚度系数Kxy变化趋势发生翻转,Kyx则随Ω增加不断减小,增加瓦块预负荷,交叉刚度系数均进一步提高。微型多叶和圆柱气体轴承的直接阻尼系数Dxx,Dxy和交叉阻尼系数Dyy随扰动频率的增加而逐渐降低,无量纲轴颈扰动频率对微型圆柱轴承的Dyx几乎没有影响。随着预负荷系数增加,两种轴承的Dxx,Dxy和Dyy有所增加,这是由于瓦块预负荷变大,气膜厚度减小对稀薄气流的阻碍作用也增强。而交叉阻尼系数Dyx随m的增加而减小。相比瓦上承载方式,瓦间承载微型多叶轴承的Dxx较小而Dyy较大,出现这种现象的原因是超薄气膜主要支承竖直方向的轴颈质量,瓦间承载的Dyy更大有利于提高轴承的稳定性。当扰动频率较大时,各动态阻尼系数曲线最终趋于重合。
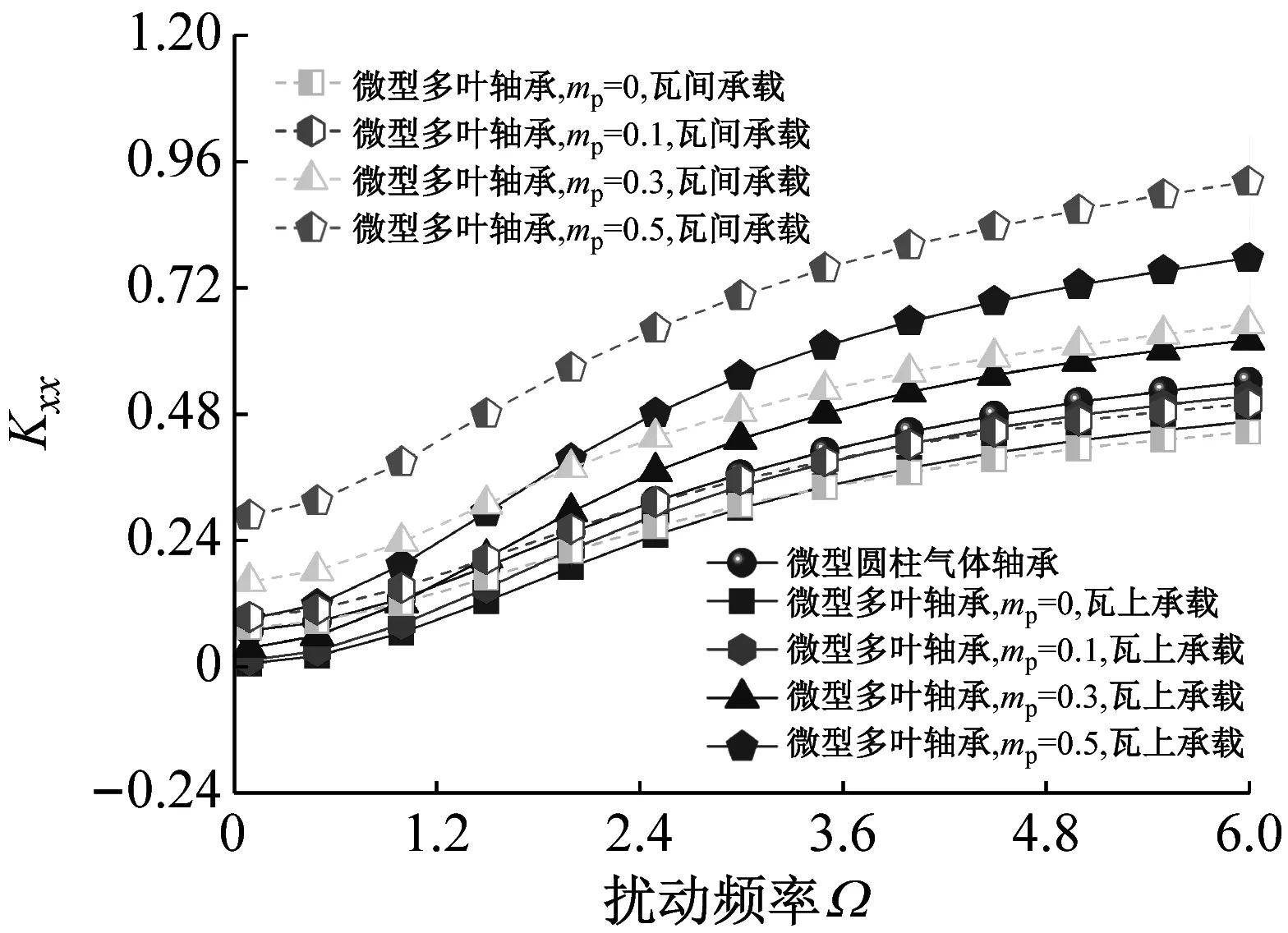
(a) Kxx vs.Ω
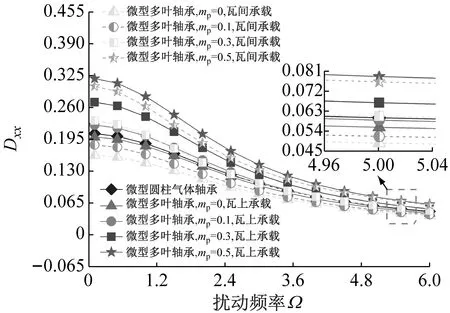
(a) Dxx vs.Ω
当B/D=0.1,Λ=10和Ω=5时偏心率ε对微型多叶轴承和微型圆柱气体轴承的动态系数的影响规律,如图5、图6所示。随偏心率的增加,各刚度系数加速上升,预负荷系数增大进一步提高了动态刚度系数。瓦间承载微型多叶气体轴承的刚度系数均大于瓦上承载方式,且偏心率越大,两者动态刚度系数结果差值越大。瓦块预负荷较高,瓦间承载微型多叶气体轴承的刚度系数大于相同参数的微型圆柱轴承。这是因为偏心率和预负荷系数变大均为降低了最小气膜厚度,增强了微型轴承内薄膜压力,同时压力峰值附近瓦块前缘入口处泵送更多气体进入轴承间隙,大幅提高了润滑气流密度,进而超薄气膜刚度增加。当ε<0.6时,瓦上承载的交叉刚度系数几乎与偏心率无关,ε>0.6后Kxy和Kyx变化曲线发生翻转。随着偏心率增加,两种轴承的直接阻尼系数逐渐增大,预负荷系数在偏心率相等时明显提高了阻尼系数的直接项,但大偏心率下会降低微型多叶轴承的交叉阻尼系数。当ε<0.4时,瓦上承载和瓦间承载的Dxx和Dyy曲线接近重合,随着偏心率继续增大,不同承载方式的直接阻尼差异开始显现,瓦上承载的Dxx偏大,而瓦间承载的Dyy略大。瓦上承载微型多叶轴承的交叉阻尼系数则表现出先降低后增加的变化趋势。可以看出,与动态刚度系数类似,瓦块预负荷较大时,瓦间承载多叶轴承的阻尼系数均超过微型360°圆轴承,说明选择合适的预负荷系数和瓦块分布位置可有效提高微型多叶气体轴承润滑性能和稳定性。

(a) Kxx vs.ε
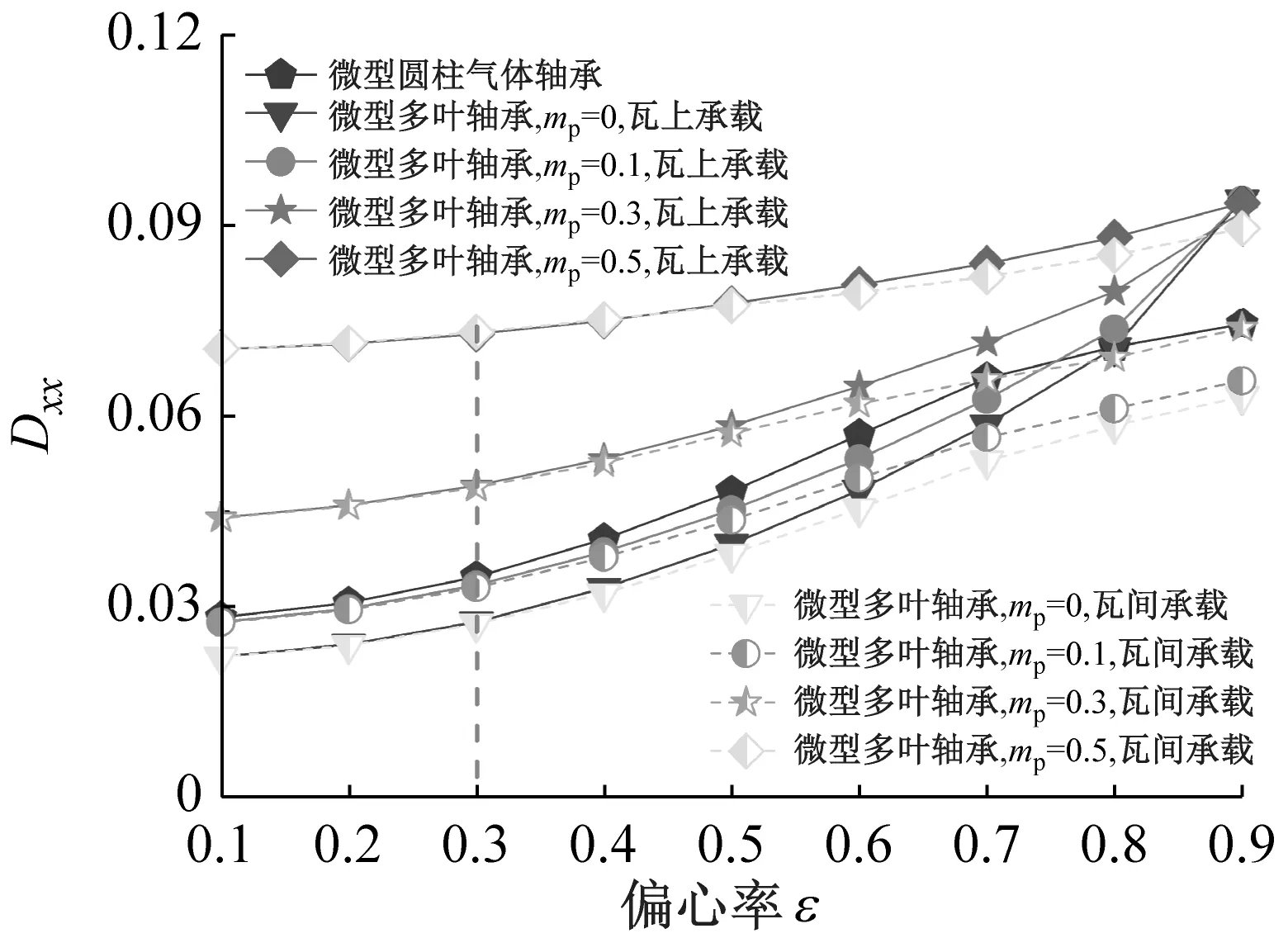
(a) Dxx vs.ε
轴颈转速、瓦块分布位置和预负荷系数对微型多叶气体轴承和微型360°圆轴承动态刚度和阻尼系数的耦合作用,如图7、图8所示。直接刚度系数均随ω的增加而增加,除了预负荷系数m=0.5和ω>3×105rad/s时,瓦上承载微型多叶气体轴承的刚度系数Kyy较大,瓦间承载轴承的直接刚度系数大于瓦上承载方式。这是因为在极高转速和大轴瓦预负荷下,轴承间隙变小,稀薄气体高速流动,瓦间沟槽泵入的外部气体不足以补充高速轴颈带走的润滑剂,气体稀薄程度没有得到改善,此时微型多叶轴承瓦上承载的支承刚度更大。瓦上承载的Kxy和Kyx随轴颈转速的增大先减小后增加,而微型多叶轴承瓦间承载的交叉刚度系数呈现出减速上升最终趋于定值。预负荷系数越大,微型多叶轴承的动态刚度系数也越大,还需注意到,瓦块预负荷越大,各刚度系数接近稳定值的轴颈转速越高,说明了较大的预负荷系数会导致轴承进入平稳运行状态时间延长。相同轴颈转速条件下,瓦间承载微型多叶轴承的交叉刚度系数最大,微型圆柱气体轴承次之,微型多叶轴承瓦上承载方式最小。两种轴承的动态阻尼系数Dxx和Dyy随轴颈转速增加均先快速增大接着略微下降,这是由于不同结构参数的轴承起飞转速不同,微轴承未完全形成超薄气膜润滑,转子主要靠各瓦块联合提供支承,随着转速进一步提高,转子质量改由气膜支承,刚度系数相应会减小。动态阻尼系数的直接项随预负荷系数的增加而增加,其原因是稀薄气体润滑膜主要在竖直方向支承轴颈质量,当瓦块预负荷较大时,高轴颈转速增强了微轴承的动压效应和瓦间沟槽的“泵吸效应”,加剧了更小轴承间隙内稀薄气体的相互作用,超薄润滑气膜在运动方向的Poiseuille流动阻碍越大,因此微型多叶气体轴承瓦间承载的Dyy也较大。多叶轴承瓦上/瓦间承载方式的交叉刚度系数表现出相反的变化趋势,且随轴颈转速逐渐增大最终趋近于零。

(a) Kxx vs.ω

(a) Dxx vs.ω
当ε=0.5,Λ=12,Ω=3时微型多叶/圆柱气体轴承动态系数与长径比、预负荷系数及瓦块分布位置间的相互关系,如图9、图10所示。

(a) Kxx vs.B/D
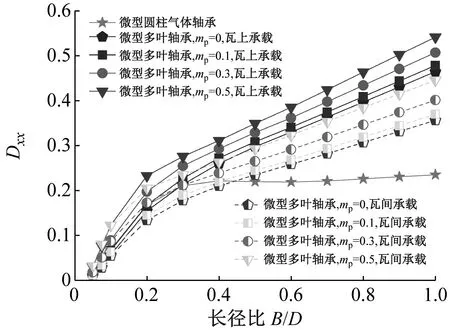
(a) Dxx vs.B/D
由图9、图10可知,动态刚度系数均随长径比增加近乎线性增大,这是由于长径比增加,微型气体轴承宽度越大,各瓦块有效承载和润滑薄膜面积提高。相比常规尺寸气体轴承,实际硅基微型动压气体轴承的长径比通常取0.05~0.10,可以看出,较小长径比范围内各刚度系数差值不大。随着预负荷系数增加,大长径比下动态刚度系数增幅也越大。m=0.5微型多叶轴承动态刚度系数的直接项超过了同等结构参数的360°圆轴承。当B/D>0.2,除了瓦上承载方式的Kyy较大,其余微型多叶气体轴承瓦间承载的刚度系数更大,其原因是长径比和瓦块预负荷越大,气膜间隙变薄,微小空间内气流不畅,瓦间沟槽和轴承两端外泄气体多于“泵吸效应”流入瓦块的润滑剂流量,稀薄效应和不连续气膜的负面影响愈发明显。随长径比增加,Dxx,Dxy和Dyy先快速增大,接着以更小斜率逐渐线性增加,而动态阻尼系数Dyx则表现出先降低后增大最终再下降的变化趋势。提高预负荷系数,直接阻尼系数有所增加,当B/D>0.4,瓦上/瓦间承载多叶轴承的Dxx和Dyy均超过微型圆柱轴承,这说明选用微型多叶气体轴承可有效提高微型轴承-转子系统的稳定性。与长径比和瓦块预负荷对直接刚度系数的影响规律不同,相比瓦间承载方式,瓦上承载的Dxx更大,Dyy更小。在B/D=0.2处,微型多叶轴承瓦上/瓦间承载的交叉阻尼系数发生翻转。产生这种现象的原因是长径比较大时静态和扰动压力沿周向变化明显,对瓦块位置变化敏感,多个轴瓦间稀薄气流相互影响愈加复杂。
3 结 论
为揭示微型多叶动压气体轴承的润滑机理,基于前期作者针对微型圆柱气体轴承动态特性计算方法的工作,本文推导了稀薄气体润滑完整变量频率扰动的动态修正Reynolds方程,利用偏导数法、有限差分法和超松弛迭代法联立求解。详细研究了预负荷系数、瓦块分布位置及轴承参数对超薄气膜刚度和阻尼系数的影响规律,并与微型360°圆轴承动态特性进行对比,得到如下结论:
(1) 轴颈扰动频率和预负荷系数均提高了瓦上/瓦间承载微型多叶轴承的直接刚度系数。与常规尺寸多叶轴承存在瓦间沟槽会降低气膜刚度不同,轴向沟槽泵吸外部气体弱化了稀薄效应,微型多叶气体轴承瓦间承载方式刚度系数的直接项更大。瓦块预负荷增加降低了最小气膜厚度,稀薄气流受到的阻碍作用变强,当无量纲扰动频率较大时,所有动态阻尼系数曲线最终趋于重合。
(2) 瓦块分布位置在偏心率较小时对微型多叶轴承的直接刚度和阻尼系数影响很小。偏心率和预负荷系数均会大幅降低气膜间隙,瓦间沟槽吸入的气体显著提高了稀薄气流流量,大偏心率条件下其超薄气膜刚度系数增幅明显,且当预负荷系数较大时微型多叶轴承瓦上/瓦间承载的动态阻尼系数高于微型圆柱气体轴承,说明合适的瓦块预负荷和偏心率对提高微型轴承-转子系统的稳定性有利。
(3) 随轴颈转速增加,微型气体轴承的动压效应和瓦间沟槽的“泵吸效应”增强,Kxx和Kyy有所增加,微型多叶轴承瓦间承载的交叉刚度系数最大,微型圆柱轴承次之,瓦上承载方式的多叶轴承最小。另外,微型多叶轴承瓦上/瓦间承载方式的直接和交叉刚度系数呈现出相反的变化趋势。由于增加长径比提高了轴瓦承载和超薄气膜面积,动态刚度系数随长径比增加近似线性增加,当B/D>0.4时,瓦上/瓦间承载微型多叶轴承的直接阻尼系数大于微型圆柱气体轴承,各瓦块稀薄气体相互作用更加复杂。
综上所述,相比微型360°圆轴承,微型多叶气体轴承兼容超精密加工技术,结构相对简单,瓦间沟槽有效散热及稳定性较好等优点,可作为支承微型高速转子的有益轴承类型。
