基于几何条件的可倾瓦轴承油膜边界条件判定方法
2015-12-05荆建平陈昌敏
季 超,荆建平,2,3,陈昌敏
(1.上海交通大学 机械系统与振动国家重点实验室,上海 200240;2.上海交通大学 振动噪声研究所,上海 200240;3.上海交通大学 船舰设备噪声与振动控制技术国防重点学科实验室,上海 200240)
基于几何条件的可倾瓦轴承油膜边界条件判定方法
季 超1,荆建平1,2,3,陈昌敏1
(1.上海交通大学 机械系统与振动国家重点实验室,上海 200240;2.上海交通大学 振动噪声研究所,上海 200240;3.上海交通大学 船舰设备噪声与振动控制技术国防重点学科实验室,上海 200240)
针对可倾瓦轴承的雷诺方程,基于瓦块几何模型获得各个瓦块的边界条件,利用轴心、各瓦块中心与轴承之间的耦合关系,采用有限差分法计算分析油膜压力的分布。理论推导表明,瓦块的位置仅由瓦块预置参数、轴心的位置决定;数值结果表明,轴承的承载力随偏心率增大呈增大趋势。结合具体算例看出,当轴颈位置确定时,可确定各瓦块实际偏位角和偏心率,进而可对各瓦块方程分别进行求解。建立一种可行的边界条件确定法则,为可倾瓦轴承的建模提供了理论依据。
振动与波;油膜压力;可倾瓦轴承;几何关系;边界条件;偏位角
可倾瓦轴承由于其较好的稳定性[1]使得其在转子系统中得到广泛的应用。但是在实际工程中,以可倾瓦轴承为支承的转子系统的失稳现象[2,3]仍时有发生。而油膜力的分布[4]在整个可倾瓦轴承系统的失稳现象中起着非常重要的作用,其精度决定了对转子行为分析的准确度[5],因此需要建立可倾瓦轴承油膜力分布求解的模型。
目前关于可倾瓦轴承的求解已有不少可行的方法,如直接求解法[6]、数据库法[7]等等,但这些方法在求解瓦块的雷诺方程时,基本都默认以瓦块的起始边和终止边上的油膜力均为0,瓦块内部满足雷诺边界条件来进行计算,但是根据动压油膜的生成条件可知,轴承的各个瓦块不一定在各个转角位置下均可以生成动压油膜或者油膜起始边界不一定在瓦块的起始边,因此需要加入可行的判定条件。
本文以四瓦瓦间载荷式可倾瓦轴承为研究对象,基于动压油膜的形成条件以及各个瓦块之间的偏心距和偏位角的耦合关系,采用雷诺边界条件,推导出可倾瓦轴承各个瓦块上雷诺方程求解的油膜边界条件,为可倾瓦轴承求解提供理论参考。
1 可倾瓦轴承各瓦块耦合关系
图1、2所示为可倾瓦轴承的瓦块在发生摆动前后的几何关系图,其中Oj为轴颈中心的位置,轴颈半径为R0,O为轴承中心位置,O1、O2分别代表瓦块在摆动前后的圆心位置。Φ为该瓦块相对于竖直方向的安装角度。

图1 摆动前瓦块的几何关系

图2 摆动后瓦块的几何关系
假设轴颈相对于轴承的偏位角为θ,偏心为e,瓦块的预置偏心为e0,轴颈相对于瓦块的实际偏位角为γ,偏心率为e1,则由此可以得到可倾瓦轴承各瓦块的偏心率、偏位角与e和θ的关系。
设轴承半径为r,轴瓦的厚度为 h0,则知

在图1三角形AOOj中由余弦定理可得到
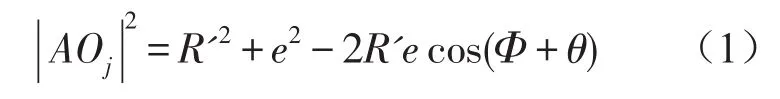
在图2三角形AO2Oj中由余弦定理可得到
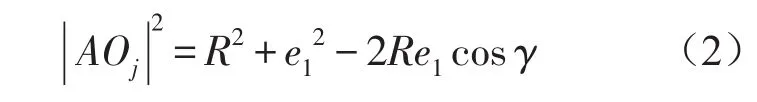
由(1)(2)两式相等可得到关于 e1的方程:其中


解此方程可得e1为轴颈相对于瓦块中心的真实偏心距,则可以知道其取值范围是记半径间隙为C=R-R0,则e1∈(0,C)。
基于此可以得到各个瓦块的实际偏心距与e之间的关系,在求解雷诺方程时,轴承相对于各瓦块的偏位角可以由瓦块的力矩平衡方程[8]进行修正,而e则可以由轴承的静载荷进行修正,所以在此基础上可以修正可倾瓦轴承的雷诺方程求解过程。

图3 修正后雷诺方程求解过程
2 求解雷诺方程的边界条件
在求解雷诺方程时,由于轴颈相对于各个瓦块的实际偏位角是不同的且一直在改变,所以各个瓦块的求解边界条件各有不同。
由于动压油膜的形成需要满足三个条件[9]:
(1)相对滑动的两表面必须形成收敛的楔形间隙;
(2)被油膜分开的两表面必须有足够的相对滑动速度,其运动方向必须使润滑油由大口流进,小口流出;
(3)润滑油必须有一定的粘度。对于滑动轴承而言,动压油膜是否形成,主要是看转子的转动方向与楔形间隙收敛方向的关系。
图4表示了不同轴心位置时,瓦块油膜的形成情况。假设偏位角γ的正方向为顺时针,且轴颈的旋转方向同样为顺时针。瓦块的起止角度φ1、φ2以φ0为起点来计算,即φ0=0。
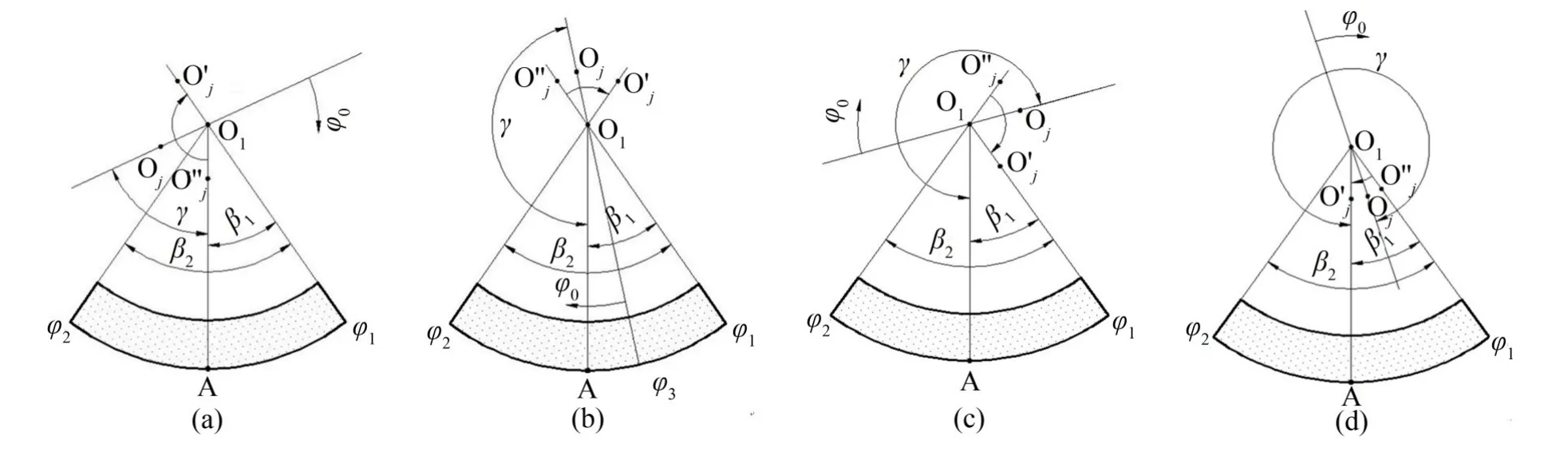
图4 轴瓦上动压油膜形成的情况
由雷诺边界条件结合有限差分法求解雷诺方程时,油膜的终止边界可以由雷诺边界条件求出,所以在求解时只需要判定起始边即可。从图4(a)中可以看出,当轴颈中心Oj从O''j运动到O'j的过程中,瓦块起始边始终在可以形成动压油膜的范围内,所以求解的边界条件是:

此时,0≤γ≤π-β1。
同样,从图4(b)、(c)、(d)中可得到其他情况下的边界条件如下
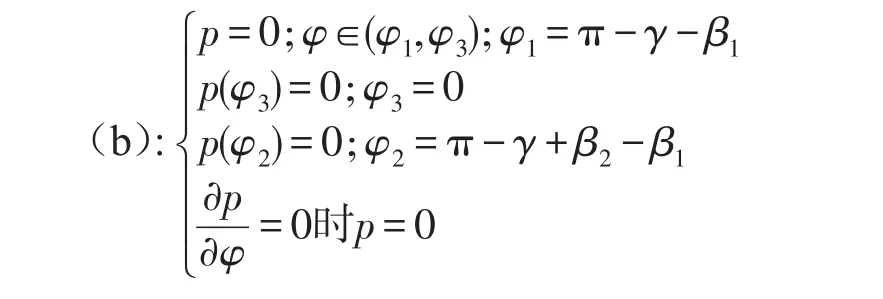
此时,π-β1≤γ≤π-β1+β2
(c):瓦块上未形成动压油膜。

由此边界条件进行相应的判断,可以求出油膜的压力分布,并进一步求出瓦块所受到的切向力Fta和径向力Fra。力的正方向如图5所示。

图5 瓦块受力的正方向

根据瓦块的力矩平衡条件可知,瓦块受到的力的方向必须经过瓦块的转动中心,即合力方向通过A点。所以在迭代实际偏位角γ时,只需要满足条件Fta=0,即可保证瓦块的力矩为零。
3 算例
由以上分析可以看出,可倾瓦轴承各个瓦块形成动压油膜是需要一定的条件的。在以下两种情况下有可能不会形成动压油膜:
(1)不满足动压油膜形成的三条件;
(2)满足动压油膜的形成条件,但是形成的油膜对瓦块的力始终不满足力矩平衡的限制条件,最终瓦块摆向不能形成动压油膜的位置。
以上两种情况均有可能导致某个瓦块上没有形成动压油膜。
本文以四瓦可倾瓦轴承为例,考虑瓦块形成动压油膜的边界条件,对可倾瓦轴承的承载能力和油膜分布进行求解。在不同偏心率下对轴承承载能力进行求解可以得到轴承承载能力的变化趋势如图6所示。

图6 承载能力随偏心率的变化趋势
由图中可以看出,承载能力随偏心距的增加而不断提高。取偏心率分别为ε=0.2和ε=0.5求解轴承的压力分布,得到结果分别如图7、图8所示。
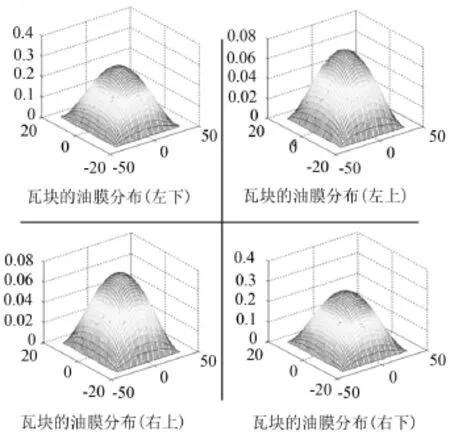
图7 ε=0.2时的油膜分布
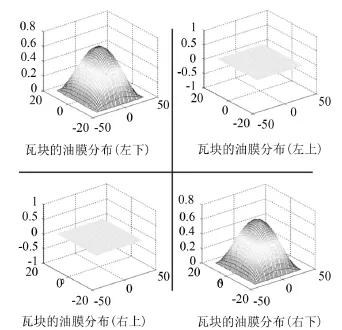
图8 ε=0.5时的油膜分布
从图中可以看出,在ε=0.2时,可倾瓦轴承的各个瓦块上均形成了油膜分布,但是下面两个瓦块的油膜力明显比上边两个瓦块大,相差一个数量级;当ε=0.5时,仅下边两个瓦块形成了油膜,而上边两个瓦块上没有形成油膜分布。综上可知,并不是每个瓦块上都会形成油膜分布,所以在求解各个瓦块的动压油膜的分布时,要依据相关条件进行边界条件的判定。
对左上位置瓦块进行分析如图9所示,瓦块上切向力很小,基本为0,满足力矩平衡的要求,而瓦块上的径向力随偏心率的增大不断减小。瓦块的受力情况与轴颈位置、轴承参数都有很大关系,当轴承和轴颈位置确定时,在本算例中得到,ε=0.375时轴承的径向和切向力都很小,基本为0,即此时该轴瓦已经不会再形成动压油膜。

图9 左上瓦块所受力随偏心率的变化
同时对比ARMD软件仿真结果如下,ε=0.35时上瓦块可以形成油膜,ε=0.4时两上瓦块不形成油膜,由此验证理论结果的必要性和正确性。
4 结语
本文推导了可倾瓦轴承油膜分布求解时不同条件下的边界条件,结合具体算例可看出当偏心率较大时,部分轴瓦并不一定形成动压油膜或者油膜的起始边界并不在瓦块起始边界,因此在低速重载时需要考虑油膜边界的影响,从而论证了边界条件判断的必要性,为求解可倾瓦轴承的雷诺方程提供了相关理论参考。
Analysis of Oil Film Boundary Conditions of Tilting Pad Bearing Based on a Geometrical Model
JI Chao1,JING Jian-ping1,2,3,CHEN Chang-min1
(1.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University, Shanghai 200240,China; 2.Vibration and Noise Institute,Shanghai Jiaotong University,Shanghai 200240,China; 3.Key Discipline Laboratory for National Defense for Ship Equipment Noise and Vibration Control Technology,Shanghai Jiaotong University,Shanghai 200240,China)
The geometric model describing the boundary conditions of tilting-pad bearings was studied.The coupling effect of the shaft axis,pad center and bearing center locations was analyzed to solve the Reynolds equation and analyze the film pressure distribution by means of finite difference method.Theoretical derivation indicates that the position of each pad is determined by preset parameters and the location of shaft center only.Numerical results show that the bearing capacity increases with the increase of the eccentricity ratio.A case study demonstrates that once the shaft center location is determined,the angle of displacement and the eccentricity ratio can be determined correspondingly,thus the dynamic equation of each pad can be solved.The feasibility law of the boundary conditions has been established,which provides a theoretical basis for the modeling of tilting pad bearings.
vibration and wave;film pressute;tilting pad bearing;geometric model;boundary condition;angle of displacement
TH133.3
A
10.3969/j.issn.1006-1335.2015.03.017
1006-1355(2015)03-0078-04+158
2014-10-09
国家自然科学基金(11272204);上海交通大学燃气轮机研究院科研基金
季超(1990-),男,江苏淮安人,硕士生,主要研究方向:转子动力学。E-mail:jichao@sjtu.edu.cn
荆建平,男,教授。E-mail;jianpj@sjtu.edu.cn
