脉动环状流作用下输流管道的非线性振动特性分析

2023-11-14周云龙米列东

振动与冲击 2023年21期

周云龙,米列东

(东北电力大学能源与动力工程学院,吉林吉林 132012)

随着国民经济的快速发展,输流管道系统在石油、化工、电力等行业起着至关重要的作用。然而,因内部流体的流动引起的管道振动现象普遍存在。当管内流体的流速达到一定值时,管道结构会变得不稳定甚至破坏[1-2]。显然,管道振动特性与其流体的流动特性密切相关。对于环状流,气、液两相介质的速度相差几十倍甚至数百倍且液膜厚度很小而常被忽视。然而,液、气的密度相差数百倍,进而使得液、气两相速度归一化后相差无几,但二者的单位长度质量相差很大。此外,管道系统会因管内流体的脉动产生参数共振等丰富的动力学变化。因此,对液相速度及其脉动特性引起管道的振动特性变化的研究是至关重要的。

输流管道振动是典型的流固耦合问题。近几十年诸多学者做了大量的研究。Liang等[3]对旋压流体输流管道进行了大量的研究,结果表明当管内流体的流速达到临界值时管道发生失稳。Yang等[4-5]分析了输流管道振动特性。梁峰等[6]研究了外部周期激励下两端固定输流管道伴随内共振的非线性受迫振动问题。柳博瀚等[7]探讨了管内流动对海洋柔性管道振动的影响。孟丹等[8]对管内流动和管外流动共同作用下的管道振动特性进行了研究。这些学者都关注单相流输送管道共振参数问题,并且指出随着液速的增加,管道固有频率降低。

工程上,气液混输的现象十分普遍。多相流诱导的管道振动受到了广泛关注。Liu等[9]指出管道在段塞流态下振动最大。Miwa等[10]对流致振动进行了细致的总结并指出在段塞流和环状流态下管道振动明显,同时强烈建议应重点关注环状流的流致振动特征。Riverin等[11]在11种试验条件对U型接头和T型接头进行应力测试,结果表明应力与两相流过程中截面内气体含量的变化有关。Liu等[12-13]对水平气-液段塞流输流管道固有频率进行了研究,结果表明固有频率受段塞流间歇性影响较大,固有频率呈现间歇性变化。Ortiz-Vidal等[14]认为两相流的流动参数直接影响振动特性。刘刚等[15]对环状流管道振动模型进行了研究,并分析了固有频率的变化情况。

在工程应用过程中由于泵、风机等动力设备的不稳定导致输送的介质产生脉动。已有的文献表明,两端简支的输流直管系统在脉动流的作用下管道会出现参数共振[16-18]。在工程应用过程中由于泵、风机等动力设备的不稳定导致输送的介质产生脉动。此外,对于多相流输流管道,管道内各相介质沿管线的流速并不是恒定的。为了便于计算,常采用“One-dimensional channel flow”理论计算管道内流体的流动参数[19]。

基于上述研究,有一些细节值得注意。在以往的研究中主要关注稳定的气液两相环状流水平管的振动特性。然而,液相介质的脉动将会引起管道系统非线性振动更加复杂,产生包括分岔、混沌等振动形态。因此,本文着重考虑在脉动的液相介质作用下,环状流输流管道的非线性振动特性。采用“One-dimensional channel flow”理论计算环状流输流管道内气、液相介质的速度及单位长度质量。考虑液相介质以简单的周期形式脉动。结合Euler-Bernoulli梁模型构建横向振动数学模型。采用Galerkin方法将方程离散,并将各参数进行归一化处理。通过求解方程线性部分获得管道固有频率及临界气速随表观气速、表观液速的变化规律。采用四阶Runge-Kutta法对方程进行迭代求解。采用包括位移幅值,位移-速度相图以及位移的功率密度谱(power spectral density,PSD)等手段来研究管道系统非线性振动特性。

1 环状流水平输流管道横向振动模型

两端简支环状流输流管道系统,如图1所示。气、液相分别以表观流速uSG和uSL从入口流入并在管道内形成环状流从出口流出。系统由长度为L,截面积为Ai,抗弯强度为EI的水平直管及两端简单支撑构成。

图1 输送环状流两端简支管道系统示意图

研究基于以下假设：①管道不计剪切力的影响采用Euler-Bernoulli梁模型描述;②忽略外部阻尼的影响;③管道材料为黏弹性,且符合Kelvin-Voigt假定。

对于两端简支的水平管道系统,管道在振动过程中因弯曲变形而伸长产生附加轴力。此外,根据Païdoussis[20]忽略重力效应影响。基于Dai等[21]和Monette等[22]的研究结果,考虑轴向附加力忽略重力效应的影响时,输送气-液两相环状流的运动方程可以写为

(1)

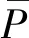
uSL=HLFuL

(2)

uSG=(1-HLF)uG

(3)

式中：HLF为液膜持液率;uL,uG为气、液相真实流速,因此单位长度气、液质量mL=ρLAiHLF,mG=ρGAi(1-HLF)。基于气芯与液膜动量平衡

(ρL-ρG)gsin(θ)=0

(4)

式中：τF,τI分别为液-壁与气-液间的剪切力;SF,SI分别为相应剪切力作用下的湿周。分别由下式计算

SF=πdΘ

(5)

(6)

(7)

其中,

(8)

SCD=dsin(πΘ)

(9)

(10)

(11)

(12)

利用式(2)～式(12)便可以获得流动参数,具体求解过程详见Zhang等[23]的研究。

引入如下变量和参数将式(1)进行归一化处理

从中可以看出,vg,vl与各自的单位长度质量和管道长度有关。由于气、液两相介质的密度差较大,因此,即使二者的速度相差很大,但归一化后二者将相差很小。

将各分量无量纲参数代入式(1)整理

(13)

vl=u0[1+μcos(ωτ)]

(14)

式中：μ为脉动幅值;ω为脉动频率。

将脉动的液相流速代入式(13),并将脉动项和非线性项移到方程右侧

(15)

采用Galerkin离散方法将式(15)高阶偏微分方程离散化为低阶常微分方程,横向位移用式(16)表示

(16)

式中：qj(τ)为广义坐标;N为阶数,本文考虑振动前两阶振动情况因此N取2;Q=[q1(τ),q2(τ),…,qN(τ)];Φ=[φ1(ξ),φ2(ξ),…,φN(ξ)];φi(ξ)为振型函数,这里采用对应于梁模型的振型函数代替,对于两端简支管道

(17)

将式(16)代入式(15),左乘ΦT并对ξ在[0,1]进行积分,得

(18)

其中,

B=[0,-b;b,0],D=[d11,0;0,d22],

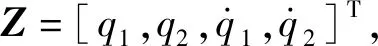
(19)

(20)

管道系统的固有频率用系数矩阵S的特征根表示

(21)

特征根Γ的虚部ω1和ω2为对应于管道系统的一阶和二阶固有频率,特征根Γ的实部r1和r2为对应于系统一阶和二阶模态的能量。管道系统的非线性振动特性采用四阶Runge-Kutta法进行求解。

2 结果与讨论

2.1 模型验证

模型分析过程中参数选择为：管道内径Di为0.025 m,外径Dout为0.032 m;管道的弹性模型E为4.35 GPa;管道密度ρp为1 180 kg/m3。两相介质采用水、空气,其密度ρL,ρG为998 kg/m3,1.209 kg/m3;气、液表观速度分别选取为uSL=0.1～0.9 m/s,uSG=20～40 m/s。根据文献[24]此速度范围处于环状流。由于缺少关于环状流管道振动位移的相关研究,采用本文方法计算获得的固有频率与刘刚等的计算结果进行对比用以验证本模型,如图2所示。值得注意的是,实部和虚部分别代表管道振动能量和频率,从图2可以看出二者吻合的很好。

(a) 一、二阶固有频率虚部

2.2 固有频率与临界气速

本节主要研究了管道固有频率与临界气速随表观气速与表观液速的变化规律。图3为管道一阶固有频率实部与虚部随表观气速与表观液速变化情况。从图3(a)中可以看出对应于每个表观液速下的管道固有频率随着表观气速增加而降低。当固定表观气速时,固有频率随着表观液速增加而降低。也就是说无论增加液速还是增加气速均会导致管道固有频率的降低。值得注意的是,表观液速对固有频率的影响更为显著。此外,当uSL≥0.5 m/s时存在临界气速,且临界气速ucr随着表观液速增加而降低。这也再次说明表观液速的增加对系统的稳定性是不利的。需要指出的是,这并不意味着临界气速只存在于uSL≥0.5 m/s系统,随着管道长度或表观气速的增加,临界气速也会发生在uSL<0.5 m/s的管道系统中。

(a) 一阶固有频率虚部随表观气、液速度变化图

从图3(c)中可以看出,当uSL=0.1 m/s时,固有频率随表观气速增加降低的幅度较为平缓,最大降幅为0.251 3。固有频率降低幅度随着表观液速增加而显著增加。

在环状流动状态下,管道内气、液两相的速度相差很大,然而二者速度归一化后相差很小,如表1所示。这主要是由于气、液两相介质的密度差造成的。在固定表观液速条件下,增加表观气速导致相间剪切力增加,因此使得液膜厚度降低,气芯面积增加,这也将导致单位长度液体质量降低,单位长度气体质量增加。因此,气、液两相介质对管道固有频率及临界气速的影响主要取决于液相介质的液膜厚度(单位长度液相质量)。

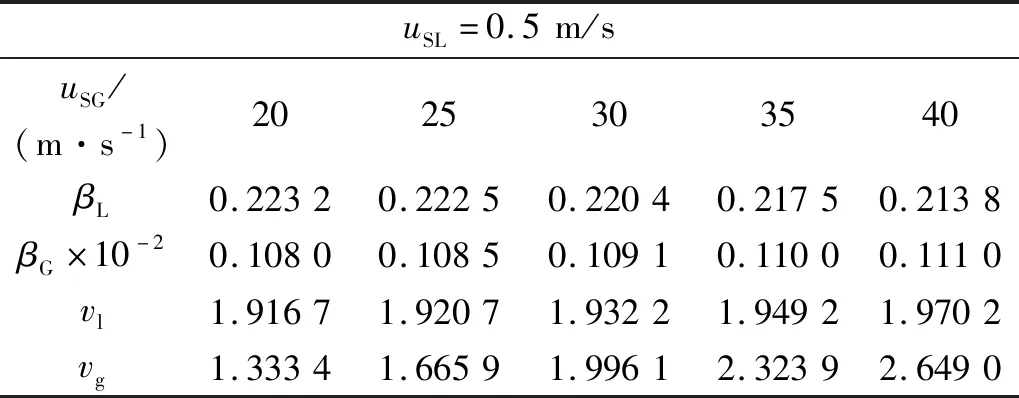
表1 归一化速度与单位长度质量

2.3 非线性振动特性

图4为在uSG=40 m/s,μ=0,ω=0条件下,以管道长度为控制参数的分岔图。从图4可以看出表观液速从0.9 m/s减小到0.2 m/s过程中,对应管道分岔起点由21.8 m增加到31.9 m。这意味着在低表观液速条件下管道更稳定。此外,随着表观液速增加位移幅值增大。值得注意的是在不考虑速度脉动时所呈现的分岔为Pitchfork分岔。

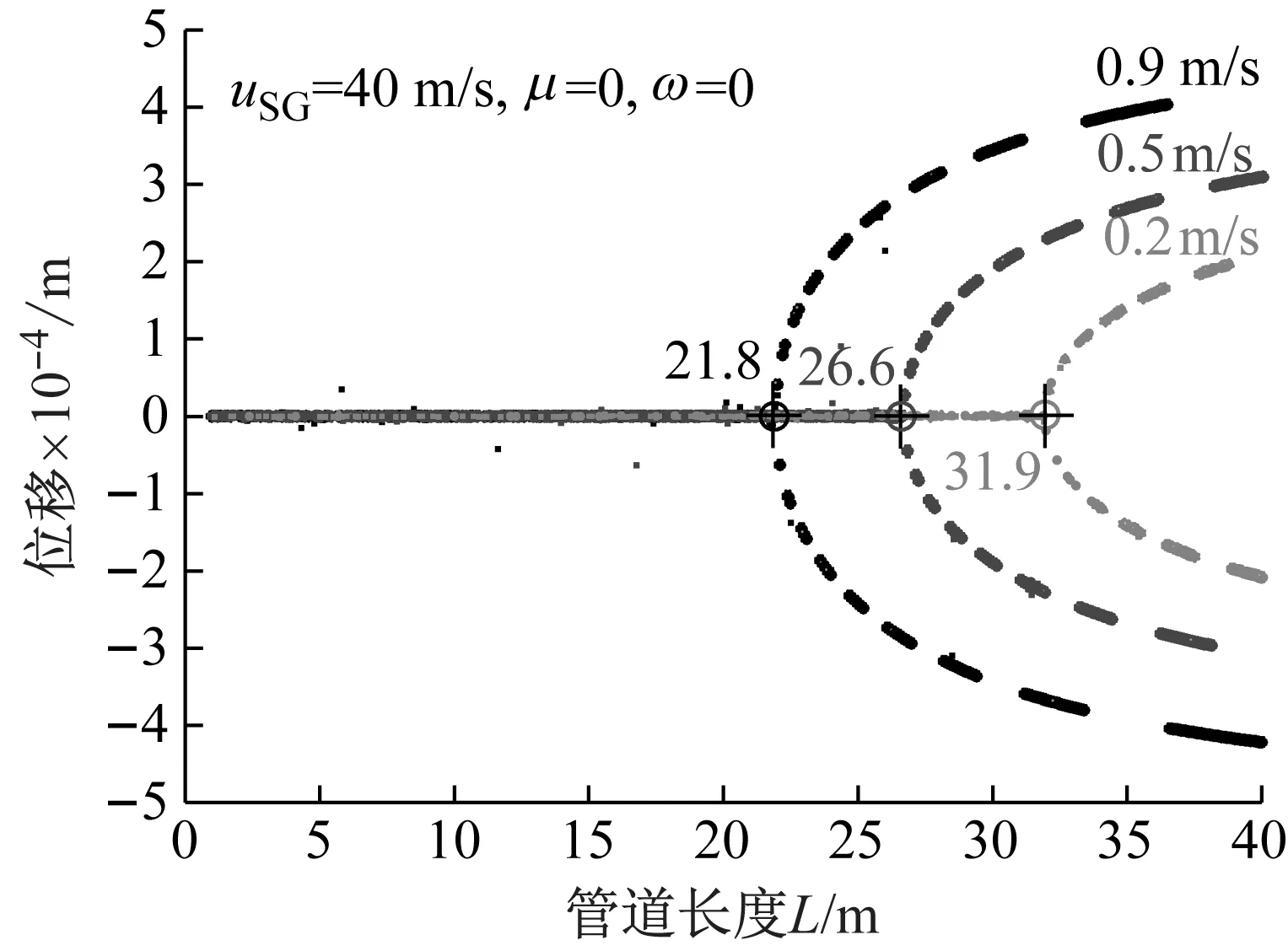
图4 不同液速条件下以管道长度L为控制参数的分岔图

图5为在uSL=0.9 m/s,uSG=40 m/s,ω=25,μ=0.4条件下,以管道长度为控制参数的分岔图。从图5可以看出,在管道长度为18.3 m处出现了分岔,随着管道长度进一步增加,系统经过多次分岔后最终达到了混沌状态。这意味着液相介质的脉动使得系统更加不稳定,而且这种不稳定将导致系统出现混沌。

图5 ω=25,μ=0.4,uSL=0.9 m/s,uSG=40 m/s条件下以管道长度L为控制参数的分岔图

对比图4、图5可以发现当考虑液相速度的脉动时,系统的分岔起始位置不仅由21.8 m降低至18.3 m而且还会使得系统的振动变得混沌。因此,有必要进一步研究激励频率对管道振动特性的影响。图6为以激励频率ω为控制参数的分岔图。基本参数如下：uSL=0.9 m/s,uSG=40 m/s,L=40 m,μ=0.4,ω=0～70。从图6可以看出随着ω变化管道振动状态发生了数次突变。然而,从分岔图中无法具体分辨出分岔路径和振动形态。

图6 以ω为控制参数的分岔图

为了能够清楚的展示系统振动形态的转换过程,借助相轨迹图、PSD以及庞加莱截面方法来研究激励频率ω=35～42变化过程中系统振动形态的变化。当ω=35时(见图7(a)),系统显示出非常混乱的轨迹线,这些轨迹线看似非常混乱但又不缺乏一定的自相似特性。从其PSD图中可以看出曲线具有宽频特性,而且庞加莱截面图显示出杂乱的点,这表明系统处于混沌状态。当ω=38.1时(见图7(b)),从其PSD图中可发现其并不具备宽频性质,只显示出一些谱尖点出现了概周期的性质,其庞加莱截面图上的点呈现一条线,说明系统处于概周期运动。当ω进一步增加至42时,系统出现倍周期和周期运动的振动形态。综上,液相流速的脉动将会导致管道系统出现包括混沌、概周期、倍周期的非线性振动形态,这与所选择的激励频率值有关。

(a) ω=35.0系统相图、PSD图以及Poincare图

此外,混沌对初值非常敏感。图8为不同初始条件下管道中心位移混沌响应。从图8(a)中可以看出当初始条件初始位移大小相等仅改变初始振动方向时,管道中心振动位移的时间响应曲线却又很大的变化,出现了大小相等但振动方向相反的现象。当初始位移方向相同仅有很小的改变由-0.001改变为-0.002,管道中心振动位移的时间响应曲线也出现了很大的不同(如图8(b)),随着时间的变化并没有出现振动的一致性。说明在这种条件下振动对初始条件极其敏感。