考虑局域接触特征的栓接结合部动力学建模表征与参数辨识

刘江南 ，龙汪鹏 †，吕剑文 ，靳启航

（1.湖南大学 机械与运载工程学院，湖南 长沙 410082；2.湖南大学 整车先进设计制造技术全国重点实验室，湖南 长沙 410082）

螺栓连接作为一种常用的机械连接方式，因其结构简单、可靠性高以及易于装配和拆卸等优点被广泛应用于各类结构系统中.然而，螺栓组的存在破坏了结构系统的连续性，其局部力学特性对结合部和系统结构的动力学性能都有不可忽视的影响［1-2］.因此，研究栓接结合部的局部接触力学特性对系统动态特性分析具有重要意义.由于栓接结合部接触作用机理复杂，影响因素众多，在不同的接触状态下具有不同的力学特性，建立具有界面特征的理论模型以及准确模拟接触行为成为研究栓接结合部动力学特性的难点问题.

国内外学者在对栓接结合部进行动力学建模时，提出了多种等效模型，如弹簧阻尼模型、薄层单元模型以及虚拟材料模型等.弹簧阻尼是表征栓接结合部动力学特性的经典等效模型，研究者包括早期的Yoshimura［3］、Kim 等［4］以及近年Li 等［5］、Armand等［6］.然而，弹簧阻尼模型忽略了单元间的耦合关系以及结合面法向和切向之间的相互影响.此外，当所需弹簧阻尼单元数量大时，与有限元集成是一个十分复杂的过程，因而不适用于多自由度复合机械系统动力学的研究.薄层单元模型来源于岩土结构力学，后在栓接结合部线性和非线性动力学研究中应用［7-10］.该模型优点在于能够快速实现对结合部动态性能的预测，但建模过程繁琐，建模结果不易用于后续的系统动力学分析和优化［11］.虚拟材料模型将被连接件表面上发生弹塑性变形的大量微凸体转化为宏观上一种虚拟介质，再依据栓接结合部的力学特性赋予其一定的弹性材料参数，从而实现动力学等效.该模型建模精度高且容易实现与其他有限元软件的结合，因而被广泛地应用于栓接结合部动力学等效中.Iranzad 等［12］将结合部等效为一层具有可变刚度特性的虚拟弹塑性材料，通过实验和预测模型相结合逆向反求出了虚拟材料参数.Zhao 等［13］在基于分形理论辨识等效弹性模量、泊松比和密度的基础上，采用非线性虚拟材料模型模拟结合部动力学行为.

基于虚拟材料建立栓接结合部动力学模型时大多将虚拟介质假设在整个接触平面，然而，预紧力在实际装配结构中的有效影响区域是有限的.研究表明［14-15］，栓接结合部接触压力从螺栓孔附近的峰值沿径向一定距离内下降至零，显示栓接结合部存在局部区域接触特征，而该特征在建立等效动力学模型时往往被忽视.孙清超等［16］、Liao 等［2］利用四阶多项式拟合结合面接触压力的不均匀分布，建立了梯度虚拟材料模型，但由于不同的接触状态下压力分布存在差异，每次建模之前均需提前拟合压力与半径之间关系，导致建模过程繁琐.此外，梯度虚拟材料模型在与有限元集成过程中，梯度层数越多，有限元模型越复杂，甚至需要开发额外的梯度单元程序［17］，难以直接用于工程实际中.因此，亟须建立一种更加符合螺栓实际接触特性且方便实用的非线性等效模型以表征栓接结合部的动力学行为.

针对上述问题，综合考虑螺栓连接结合面上明显的局域接触特征，提出一种更加符合实际装配特征的非线性局部虚拟材料等效模型以表征栓接结合部的复杂动力学特性.依据结合面横观上表现出的近似各向同性特征，建立虚拟材料微单元应力应变分析模型，理论推导虚拟材料模型的弹性模量、剪切模量和泊松比等物理参数计算方程；借鉴有限元参数化三维仿真以及数值插值校正方法快速获取螺栓在不同接触状态下的局域面压统计分布，实现对栓接结合部非线性接触区域参数的近似统计辨识.基于辨识的结合部动力学参数建立有限元动力学模型，通过模态实验与仿真结果的对比验证该方法的有效性和准确性.

1 栓接结合部等效动力学建模

结合部受到外载荷作用时，结合面间会产生多自由度、有阻尼的微幅振动，从而使结合部表现出既有弹性又有阻尼，既存储能量又消耗能量的柔性结合特性，导致结合部的模态特征方程受到接触刚度和阻尼的共同影响，而在金属结构的机械系统中接触刚度的影响远远大于阻尼［17］，因此近似将栓接结合部视为无阻尼弹性系统.

栓接结合部本质上是将两个或两个以上的零部件固结在一起，从而在机械结构中形成总成.零部件间的结合面在宏观尺度上近似平整，但实际上存在大量微凸体，各个微凸体会在预紧力的作用下发生弹塑性变形，从而表现出非线性动力学特征.将栓接结合部实际发生弹塑性变形的有效接触区域等效为一层圆柱体非线性虚拟材料单元.考虑到发生有效接触刚度特性的区域存在一定的局部特征，需要同时辨识虚拟材料模型的物理参数（材料属性参数）以及局部接触特征区域的几何参数（接触特征区域形状参数），实现集物理和几何参数一体化的栓接结合部等效动力学模型构建，如图1所示.

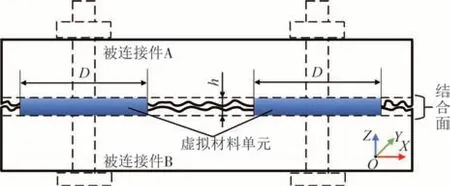
图1 栓接结合部等效动力学模型示意图Fig.1 Schematic diagram of the equivalent dynamics model of the bolted joint

虚拟材料等效动力学模型，实际上通过正交各向异性虚拟材料模拟栓接结合部局域接触刚度特性，所建虚拟材料单元各向异性参数模型如式（1），其中Z方向为接触面的法向，X-Y平面对应于接触面的切向平面.

式中：Ez，Ex，Ey，Gzx，Gzy，Gxy，υzx，υyz，υxy，ρ为虚拟材料单元物理参数，分别表示各正交向的弹性模量、剪切模量、泊松比和密度；D、h为虚拟材料单元几何参数，分别表示实际发生接触特性区域的直径和厚度.

2 栓接结合部动态特性表征参数辨识

基于局部虚拟材料单元建立的栓接结合部等效动力学模型中，动态特性表征参数包括10 个物理参数和2 个几何参数.为了求解等效模型中的物理参数，通过建立虚拟材料微单元应力应变分析模型，基于最小势能原理和吉村允孝法推导理论模型的力学计算方程；同时，为了求解等效模型中的几何参数，基于深度神经网络非线性预测方法建立区域几何参数的统计模型，实现栓接结合部不同接触状态与接触特性区域直径的非线性映射.

2.1 虚拟材料单元物理属性参数辨识

构成栓接结合部的两个粗糙结合面，其微观轮廓在切向平面内具有无序性和随机性［18］，而栓接结合部接触特性本身由微凸体的弹、塑性变形产生，使得该结合部在横观上表现出近似各向同性［19］，即：Ex=Ey，Gzx=Gzy，υzx=υyz，Gxy=

所建虚拟材料模型实际为一薄层单元，假设薄层单元应力均匀分布，任意取出一无穷小平行六面微单元体，压缩和剪切变形如图2所示.

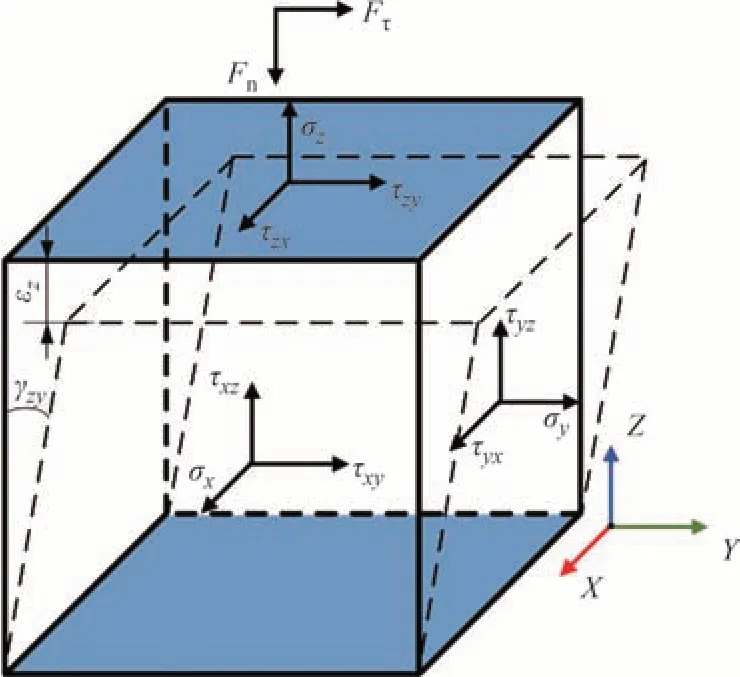
图2 虚拟材料微单元应力应变分析Fig.2 Stress-strain analysis of virtual material micro element

在受到微小的法向和切向载荷Fn、Fτ时，虚拟材料产生微小法向、切向弹性变形量Δδn、Δδτ，系统的外力功为：

等效虚拟材料在外载荷作用下的应变能为：

式中：Am为平行六面微单元体的上表面面积；hm为平行六面微单元体的高度为材料弹性逆矩阵；σ为应力矩阵；ε为应变矩阵，满足式（4）.

由最小势能原理，结构处于稳定平衡的充分必要条件为总势能最小，得：

联立式（2）～式（5），并进行体积分得：

式中：A为实际发生接触特征的面积；Kn、Kt为结合部法向和切向接触刚度，其值通过吉村允孝法获得.日本学者吉村允孝认为，结合部的接触刚度与平均接触面压有关，建立了结合部在不同接触条件下的等效刚度数据库和等效阻尼数据库［20］.根据Yoshimura法，结合部的等效刚度由式（7）计算.

式中：pn为结合部的平均面压；kn（pn）、kt（pn）分别为结合部法向、切向接触刚度.结合部的平均面压［21］由式（8）计算获得.

式中：T为拧紧力矩；D0为螺母的公称直径；ρv为等效摩擦角；βb为螺纹升角；μc为螺母与接触面之间的摩擦系数；D1为螺纹孔中径；D2为六角螺母直径.

实际上，螺栓结合面有大量的间隙存在，当任一方向发生微小弹性变形时，其他方向上不规则凸体的变形主要为填充间隙［19］，因此忽略其他方向的微小变形，即vxy=vyz=vzx≈0.由式（6）可以看出，虚拟材料等效模型上下表面之间的法向和切向刚度与横向弹性模量Ex、Ey无关，横向弹性模型本质上与结合面的紧密结合程度和当量弹性模量E'有关，因此，Ex、Ey按照式（9）进行计算，Atol表示栓接结合面总面积.

等效虚拟材料的密度参数由密度的定义计算，如式（10）所示.

2.2 虚拟材料单元几何属性参数辨识

在基于虚拟材料单元建立栓接结合部的等效动力学模型时，普遍认为接触特性发生在整个粗糙平面内，这仅适用于小接触面积或者多螺栓组的情况.然而，在机械系统中许多大型的固结表面由于实际装配空间的限制，通常只通过数个螺栓连接而成，若此时假设整个接触平面均发生接触特性显然是不合理的.同时，与圣维南原理“弹性体某一小块荷载的合力和合力矩等于零时，远离荷载作用区的应力几乎等于零”的结论相违背，因此，为了建立精确、合理的栓接结合部动力学模型，需要识别结合面上实际发生的有效接触区域，完成虚拟材料单元的几何参数辨识.

基于实验结果的逆向反求分析是动力学参数高精度辨识的有效方法［22-23］，然而，虚拟材料单元的几何参数在不同接触状态下因压力分布有所不同，在进行逆向反求之前均需搭建模态实验台，计算耗费时间长，因此存在很大的局限性.相比于逆向反求建模，基于螺栓结合面压力分布的统计学规律，建立虚拟材料单元的几何参数预测模型，虽然在前期获取统计数据时较为费时，但后续模型应用时具有较高的计算效率，被广泛应用于参数辨识中.

探究螺栓结合面上接触压力的统计分布规律是实现螺栓有效接触区域辨识的前提.如图3 所示，通过建立栓接结合部静力学模型，分析各连接零件结合面在力封闭链中的接触作用关系.螺栓头、垫片在轴向预紧力Fn作用下向被连接件A、B分别施加分布力载荷PA1、PB1，从而在结合面上产生作用力PA2和反作用力PB2.

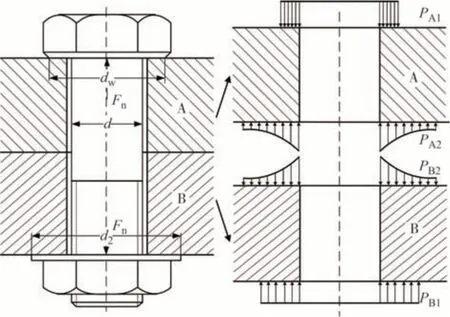
图3 栓接结合部静力学模型分析示意图Fig.3 Schematic diagram of the static model analysis of the bolted joint

采用有限元仿真的方法，模拟上述栓接结合部力学模型，在保证仿真精度的情况下实现快速获取螺栓连接在不同接触状态下的接触压力分布规律.在Ansys 软件中建立栓接结合部Solid185 实体有限元模型，为提高计算效率，将螺母内壁与螺栓节点耦合模拟螺旋副约束，此外，避免边缘效应对压力分布的影响，被连接件的横向尺寸应设置远大于螺栓直径.接触行为的模拟采用Targe170 目标单元和Conta174 高阶接触单元，并通过增强拉格朗日乘子接触算法进行数值求解.利用Prets179 单元实现螺栓的预紧效果，为防止数值求解出现近似偏差导致大位移的产生，采用远程节点位移形式约束被连接件四周节点，王磊等［24］、Kim 等［25］均证明了该建模方法具有很高的精度，能够近似等效螺栓实际连接情况.

研究表明［24］，影响栓接结合部有效接触区域的重要因素包括被连接件厚度、接触面摩擦系数、螺栓直径、螺栓预紧力等.为获取栓接结合部的结合面接触压力在不同因素状态下表现出的力学特性，完成接触压力统计学分布规律分析，在Ansys 的APDL 语言环境中建立结合部有限元参数化分析模型以及编写节点坐标和应力提取程序，基于Matlab-Ansys 协同驱动批量模拟7 000 种在不同因素下的螺栓连接接触情况.按照机床常用螺栓的参数，不同因素离散点取值如表1所示.

表1 不同因素取值表Tab.1 Table of values for different factors

以M10 螺栓在44.5%屈服极限轴向预紧力作用下固结厚度为12 mm 的被连接件有限元分析模型为例，其中被连接件的摩擦系数为0.12，将结合面节点坐标和节点压力通过APDL提取后导入Matlab中，利用三角剖分插值校正法绘制结合面拟合压力分布图，如图4 所示.结合面边缘均为零压区域，压力分布明显呈现出“断崖式”分布的特点，具有显著的局域峰值特征，形状表现为一同心圆环.其余离散抽样点的仿真结果也同样均有此类现象，结果符合圣维南原理以及文献［15］和文献［16］的观点，而由Yoshimura 法的结论可知：单位面积内相同的结合面面压具有相同的动态特性数据（刚度系数）.由此说明辨识接触特性区域几何参数对正确建立栓接结合部动力学模型尤为重要.

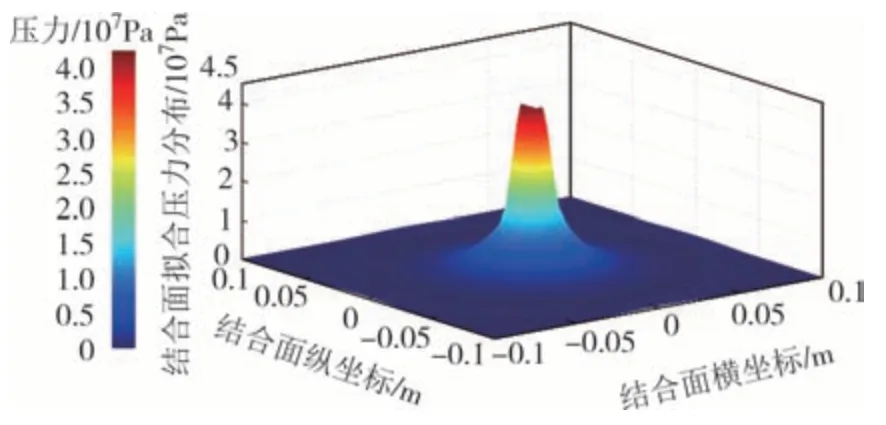
图4 结合面拟合压力分布图Fig.4 Fitting pressure distribution diagram of joint surface

辨识结合面有效接触特性区域是建立栓接结合部动力学几何参数模型的前提，由于结合面边缘部分依旧存在少许压力，这部分压力数值小且占结合面总压的比重小，无法产生有效的动态接触特性，若将该区域也认为是有效接触区域显然不合理，为此，需要确定产生接触特性的压力阈值.过大的阈值会造成存在实际接触特性的区域被误判为无效，过小的阈值会导致大螺栓接触区域压力梯度变化过大.分析上述有限元力学模型接触压力的分布规律，压力峰值Pm是接触压力分布的一个明显特征，试取压力峰值的10%作为有效接触特性压力阈值，即选取同一量级的压力区域作为有效接触区域.

为验证压力峰值的10%作为截断阈值的可行性，以文献［2］中四阶多项式插值校正拟合曲线描述结合面压力分布为例，对文献中的螺栓模型结合面压力阈值以上区域按照式（11）进行压力面积分，经计算积分后的接触压力达到整个区域压力的99.16%，即结合面几乎全部压力都集中在所设压力阈值的以上区域，因此，以压力峰值的10%作为压力阈值来确定有效接触特性区域是可行的.

式中：r1表示螺栓孔半径；r2表示压力积分外半径；Pf表示四阶压力插值拟合分布多项式.

被连接件厚度、接触面摩擦系数、螺栓直径、螺栓预紧力是影响栓接结合部有效接触区域的重要因素，因此建立栓接结合部动力学几何参数模型需要完成不同因素与区域参数的非线性关系预测.深度神经网络（DNN）因其自适应强、容错率高、结构简单的特点，随着大数据的发展被广泛用于非线性问题的预测，与其他预测模型相比，预测结果精度高、变异系数小、模型响应快［26-27］.为此，应用深度神经网络方法建立栓接结合部非线性预测模型，实现对接触特性区域几何参数的统计辨识.

DNN 模型具体结构如图5 所示，包含4 个输入（被连接件厚度、接触面摩擦系数、螺栓直径、螺栓预紧力），4个隐藏层（由传播方向各隐藏层神经元数目依次设为60、100、80、40），1 个输出（结合面接触特性区域半径）.三层神经元均采用常用的Sigmoid 和Tanh 激活函数完成各层的非线性转换，各层神经元的激活函数如图5所示.该模型以均方误差（MSE）作为代价函数评估深度神经网络预测模型的统计拟合程度，通过Adam 梯度下降算法将误差反向传播并进行迭代优化.为防止模型复杂程度高导致对几何参数数据集过拟合，加入了丢弃率为0.05 的Dropout 层以及系数为0.001 的L2 正则化处理方式，如式（12）所示，从而提高在现有数据集基础上的泛化能力.

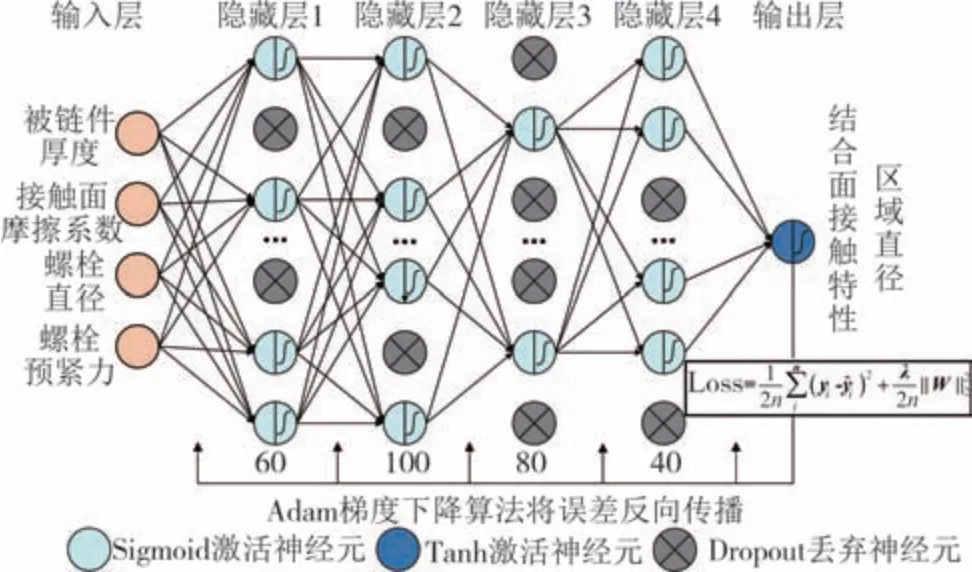
图5 深度神经网络预测模型结构图Fig.5 Structure diagram of deep neural network prediction model

式中：n为数据批量模式的数量；yi和分别为DNN模型真实值和预测值；‖W‖2为W的2-范数，W为各层权重系数；λ为正则化参数，λ=0.001.

采用图5 所示的DNN 模型预测栓接结合部有效接触特性区域面积，将7 000组栓接结合部压力分布数据按照6∶1 划分为互斥的训练集和测试集.为避免不同因素数据量级带来的误差，对原始特征数据按式（13）进行归一化处理.经过300 轮训练后，Loss误差仅为0.000 7，为评估模型训练程度，采用拟合优度R2作为预测模型性能指标，训练集、测试集的训练误差和拟合程度如图6所示.

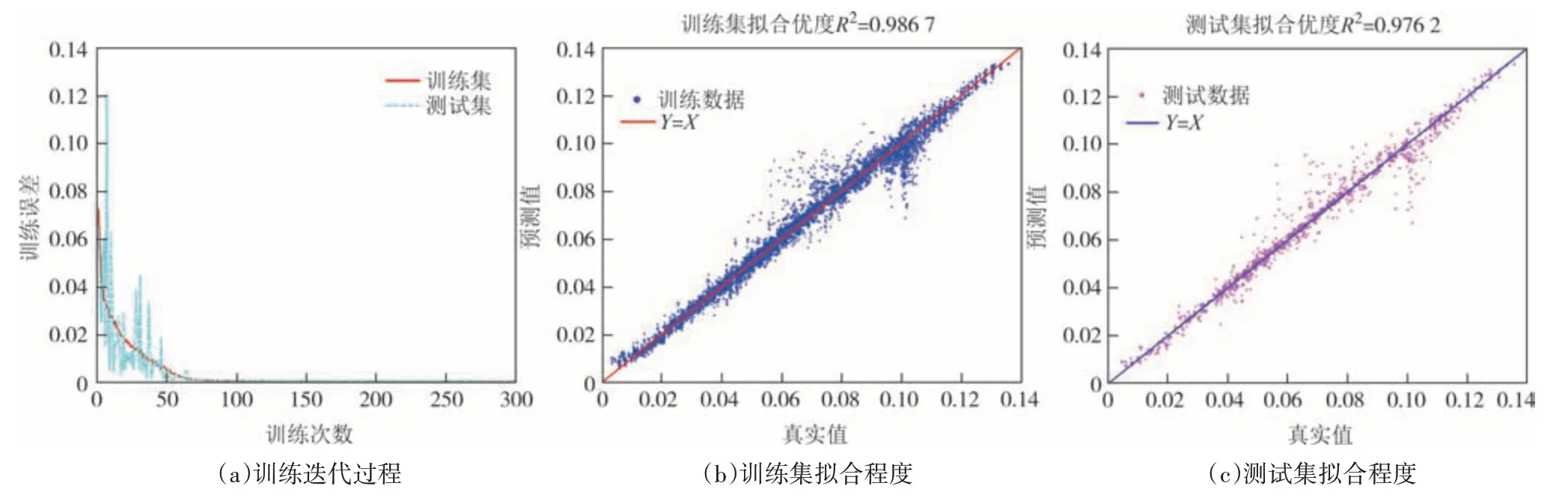
图6 深度神经网络预测模型训练结果Fig.6 Training results of deep neural network prediction model

式中：x=(x1，x2，…，xm)，表示某一因素下m个特征数据组成的集合；min（x）、max（x）分别表示特征数据集合的最小值和最大值.

如图6 所示，训练集和测试集的拟合优度分别为0.986 7 和0.976 2，表明深度神经网络模型在该问题上具有很强的预测能力，实现了栓接结合部不同影响因素与接触特性区域直径的非线性关系映射.

栓接结合部动力学模型另一个几何参数厚度h，应满足上下接触面的变形协调，即两个接触面具有相同位移，同时应避免虚拟材料厚度与其他方向尺寸差距过大，导致计算机求解时出现病态方程.此外，虚拟材料模型几何参数厚度h本质上为上下结合面上微凸体高度之和，而金属结合面发生弹塑性变形的微凸体高度h'大致在0.5 mm 上下变化［19］.为此，综合上述因素，将厚度取为2h'=1 mm.至此，已完成虚拟材料单元各向异性参数模型中12 个参数的求解.该模型充分考虑不同螺栓连接情况与局域接触刚度特性的非线性关系，使所建栓接结合部等效动力学模型相较于传统模型更具实际意义.

3 实验验证

根据上述栓接结合部等效动力学模型以及参数辨识方法，建立考虑局域接触刚度特性的结合部动力学仿真模型并进行有限元仿真分析，通过锤击法模态实验将实验与仿真结果进行对比，验证所提出结合部等效动力学建模方法的有效性.

3.1 锤击法模态实验验证与结果分析

设计并搭建如图7 所示的螺栓连接钢板模态实验装置平台，实验对象由两块相同的Q235 材质钢板和4 个性能等级为8.8 级的M12 螺栓组成，钢板的厚度为10 mm.

图7 螺栓连接钢板模态实验平台Fig.7 Modal test platform of bolted steel plate

螺栓预紧扭矩采用数显扭矩扳手测量和施加，为避免单次模态实验带来的偶然性，分别施加30 N·m、60 N·m和90 N·m的预紧力矩进行三次模态实验，由文献［28］可知螺栓的预紧扭矩与轴向预紧力的关系如式（15）所示.

式中：T表示螺栓的预紧扭矩；μt、μb分别表示螺纹副和螺栓支撑面的摩擦系数；rt、rb分别表示螺纹和螺栓支撑面有效半径；β表示螺纹牙型角；F表示轴向预紧力.

在本次模态实验中，采用弹性绳悬挂试件模拟自由边界模态.实验所得试件模态包括自身固有属性的弹性模态以及弹性绳附加的刚体模态，由于刚体模态频率远远低于弹性一阶模态，因此，忽略弹性悬挂绳对实验对象模态特性的影响.对实验对象进行模态测试时采用单点激励、多点拾振（SIMO）的测试方式，为避免单点激励导致某一阶或几阶模态丢失，选取4 个测点作为参考点进行多次测量.此外，避免因能量集中带来的实验误差，采用5 次激励实验的平均结果作为最终结果，以减少随机误差和提高信噪比，测量原理如图8 所示.所使用的仪器主要包括带SN LW43728型力传感器的力锤、三向加速度传感器以及SIEMENS SCADAS XS 数据采集分析系统，传感器将采集到的力和加速度信号传递到数据采集分析系统，数据采集分析系统将收集的数据传递给LMS Test.Lab 信号数据分析软件进行后续处理.

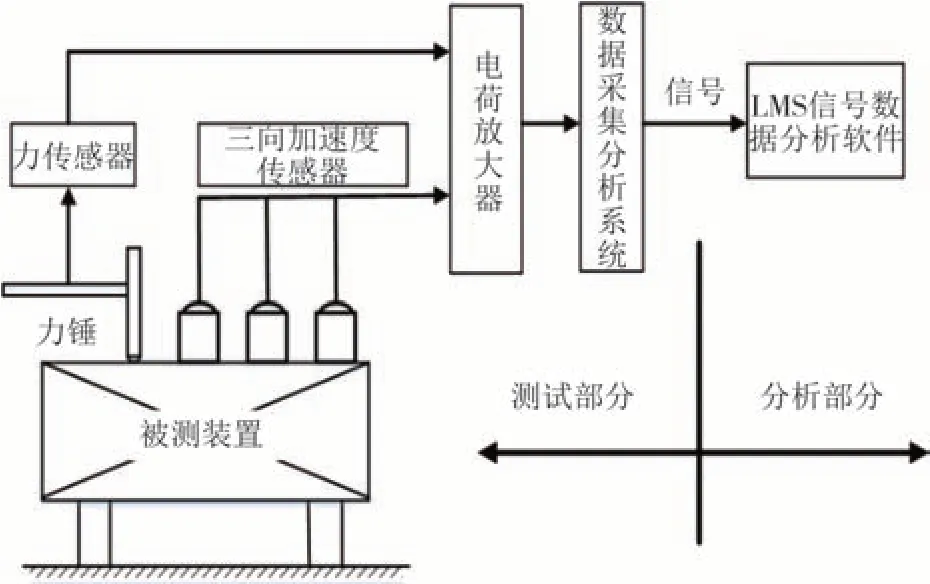
图8 测量原理图Fig.8 Measuring schematic diagram

锤击的脉冲激振实际为单位幅值的宽频带激励信号，故被测装置在被激励时能够响应更多的模态.通过LMS Test.Lab 信号数据分析软件将各测点的加速度信号进行多阶曲线拟合，拟合阶次设置为128；低阶频率在工程中更容易被激起，因此，设置频率监测范围为0～1 024 Hz.利用该软件自动选取功能辨识测试系统的前4 阶固有频率参数，实验模态固有频率与采用上述方法建立的Ansys 有限元仿真模型的对比结果如表2所示.

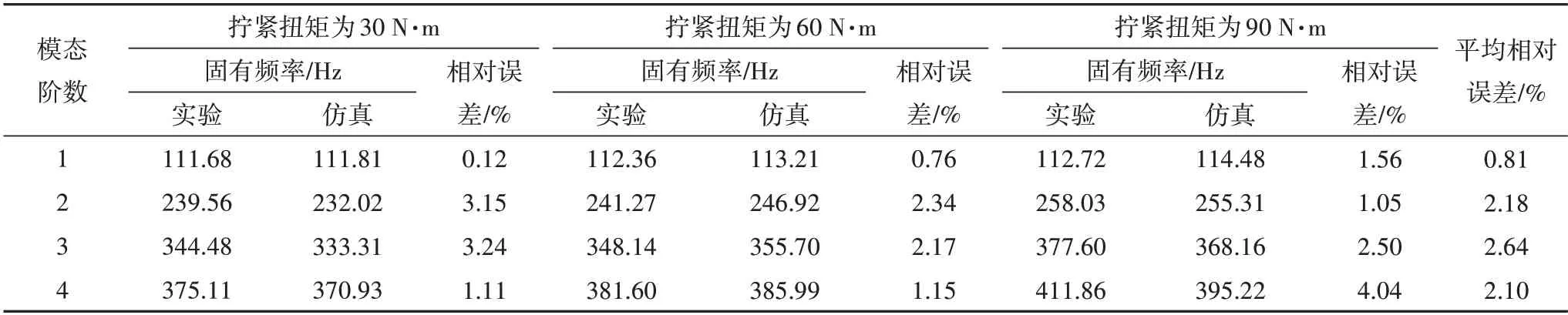
表2 实验模态参数和仿真结果对比Tab.2 Comparison between experimental modal parameters and simulation results

实验模态参数和仿真结果对比表明，仿真固有频率和实验固有频率存在少许差异，相对误差均小于4.1%，第1 阶误差在1.6%以下，最大误差出现在拧紧扭矩为90 N·m 的第4 阶模态，最大平均误差为2.64%.分析误差存在的原因，其一在于模态仿真分析中采用自由约束，但模态实验采用弹性绳约束，约束方式的差异会对测量产生影响；其二在于模态实验测试时，周围的噪声及振动也会对实验结果产生影响；其三在于几何模型的简化、有限元数值计算偏差等.通过上述三次不同拧紧扭矩的螺栓模态实验直观地看出所提出栓接结合部建模方法具有良好的准确性和有效性.

3.2 模型精度对比

传统的虚拟材料建模方法将虚拟介质假设在整个接触平面，导致不同螺栓布局的栓接结合部具有相同的动力学特性，这显然与实际相违背.为验证考虑局域接触刚度特性的栓接结合部动力学特性表征方法相对于传统虚拟材料建模具有更高的精度，另设计三组螺栓中线布局的模态实验，两种布局形式如图9 所示，将传统动力学建模仿真结果与所提出方法以及6组实验结果进行对比，如图10所示.

图9 螺栓布局形式Fig.9 Bolt layout forms

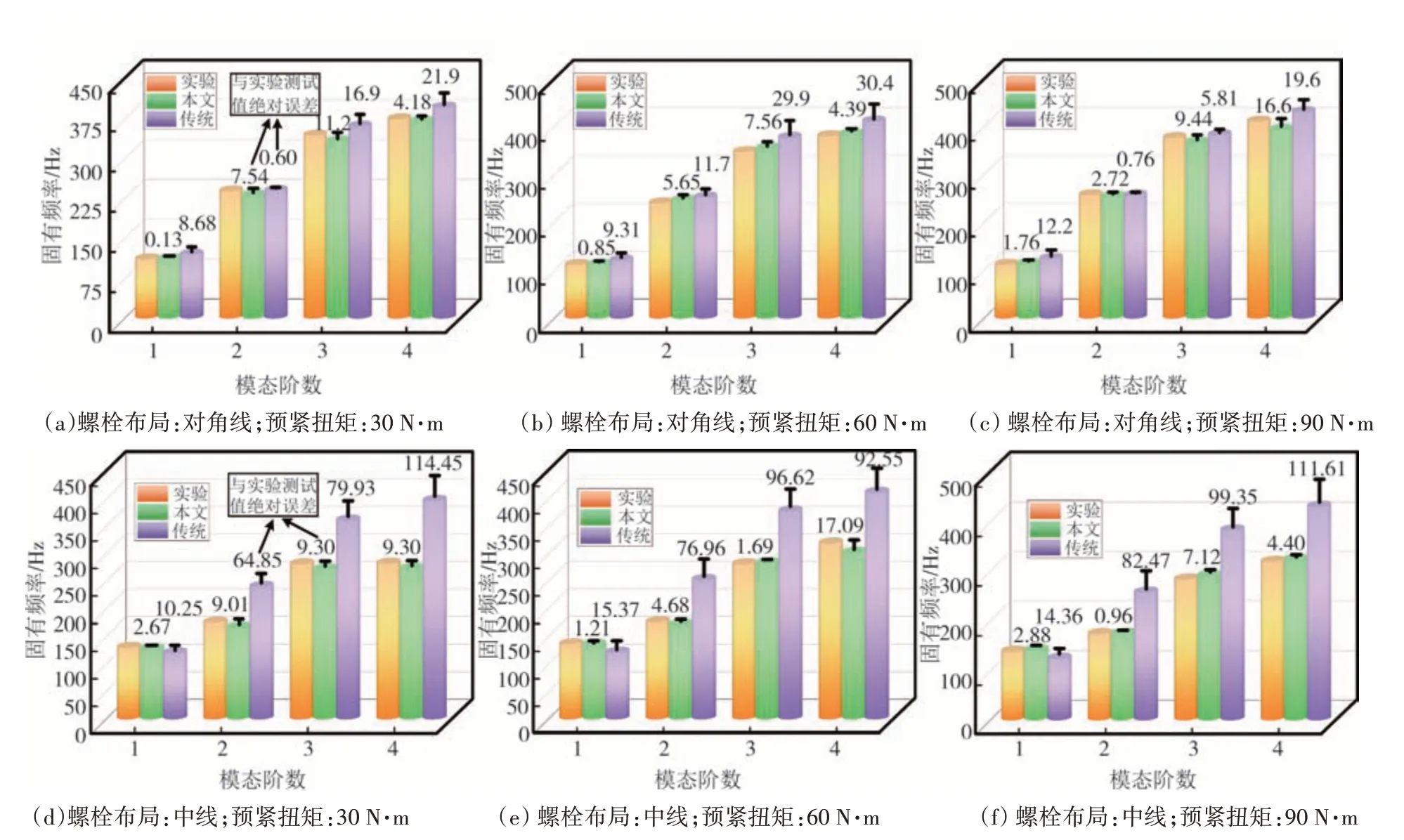
图10 两种理论模型与实验结果前4阶固有频率对比结果Fig.10 Comparison of the first four natural frequencies between two theoretical models and experimental results

可以看出，两种不同螺栓布局的金属试件系统动态特性具有显著的差别，原因在于螺栓对角线布局时的薄弱刚度位置在中线布局时得到了有效增强，致使新的振型产生，固有频率模态参数也随着螺栓布局的不同而发生改变.传统虚拟材料模型无法解释这一现象，相对于本文模型存在明显的缺陷，获得的模态参数与实验结果的偏差明显大于考虑有效接触区域的仿真计算结果.

相较于本文，传统建模方法所获得较小的参数误差主要集中在螺栓对角线布局时的第2 阶模态.三次平均误差优于本文方法0.38%，其他三阶平均模态参数偏差均大于2.37%.分析其原因在于：第2 阶模态振型表现为金属板四周中间区域的上下波状摆动，而试件所用金属钢板在加工过程中会存在一定程度的平面度误差，板材中间微量翘曲的位置在螺栓预紧力作用下会产生少量的弯曲应力.虚拟材料模型本质上是将结合面上因接触应力发生弹塑性变形的微凸体转化为弹性虚拟介质，因此，致使本文所建动力学模型与金属板实际装配情况存在些许偏差，将虚拟介质假设在整个接触平面的传统方法反而因试件平面度误差和振型的特殊性优于本文.

为进一步定量分析本文建模方法的提高精度，采用均方根误差（RMSE）作为最终评价指标来评估各阶模态参数与实验值的接近程度，RMSE的表达式如式（16）所示.

式中：n表示实验次数，即n=6；m表示参与计算的模态阶数，即m=4；fAij、fEij表示仿真计算与实验的第j阶模态参数.将图10 的数据代入式（16），获得不同建模方法下的最终综合评价RMSE值.

经计算，传统和本文建模方法的RMSE 值分别为0.234 49 和0.025 97.不同模型下最终评价指标RMSE值对比结果表明，采用基于局域接触刚度特性的栓接结合部动力学特性表征方法与实验值的偏差更小，相比较传统全局接触特性方法，RMSE 精度提高了88.9%.综上所述，所提出的采用深度神经网络预测模型实现对虚拟材料单元区域的几何参数辨识，使得建立的等效动力学模型更加符合结合部实际装配特征，相较于传统虚拟材料模型也具有更高的精度.

4 结论

本文针对目前关于栓接结合部动力学特性分析与结合部实际装配特征不符所造成的精度偏差问题，提出了一种考虑局域接触刚度特性的栓接结合部动力学特性表征方法.

1）将在预紧力作用下实际发生弹塑性变形的有效接触区域等效为一层非线性虚拟材料单元，建立了集物理参数和几何参数为一体的虚拟材料动力学模型.

2）利用最小势能原理和吉村允孝法推导了虚拟材料单元弹性模量、剪切模量和泊松比等物理接触特性参数的计算公式；综合考虑螺栓连接结合面上的局域接触特征，利用深度神经网络建立栓接结合部接触特性区域预测模型，实现了不同螺栓连接特征参数与结合面局部接触特性区域的非线性映射.

3）在考虑局域接触刚度特性的基础上，建立螺栓连接钢板结构的有限元动力学模型，通过有限元仿真分析和锤击法模态实验结果对比，前4 阶固有频率误差均小于4.1%，验证了所提出结合部动力学建模方法的合理性和有效性.并将本文方法和传统建模方法进行比较，在模态参数均方根误差评价指标上精度提高了88.9%，表明该方法具有更高的精度.

4）在某些小接触面积或者多螺栓组的工程结构中，相邻螺栓间的有效接触区域因空间位置紧凑而产生相互耦合作用，针对此类栓接结合部问题，耦合区域的力学性能应更为复杂，对系统的动态特性影响也应更为显著.后续工作将针对耦合区域的栓接结合部动力学展开研究，进一步提升模型的应用范围.