基于约束跟随理论的消防无人机水枪喷嘴跟踪控制

张新荣 ，康龙 ，张东升 ，张军

（1.长安大学 道路施工技术与装备教育部重点实验室，陕西 西安 710064；2.西安交通大学 机械工程学院，陕西 西安 710049）

随着经济的发展和人口的增长，城市规模变得越来越大，为了满足日益增长的空间需求，出现了越来越多的高层建筑甚至摩天大楼，高层建筑的消防工作已成为一个新的城市问题.传统的消防车和消防梯只能用于较低的建筑物，而对于10 层以上的更高层建筑很难实施灭火措施［1］.

近年来，无人机（Unmanned Aerial Vehicle，UAV）在民用、军事等领域发挥着重要作用，因此，受到了工业界和学术界的广泛关注［2］.由于单纯的UAV 无法适应复杂的工作需求，因此UAV 与配备水枪的云台紧密结合被应用于高层建筑消防中［3-5］.UAV下悬挂的云台装置主要用于控制水或其他灭火材料的喷洒方向.在很多情况下，找到火点后，为了达到良好的灭火效果，水枪喷嘴必须沿着期望轨迹运动，如瞄准一个固定点水平或垂直摆动、圆形或椭圆形摆动等.水枪喷嘴的运动具有两个自由度，并由两台无刷直流电机（Brushless Direct Current Motors，BLDCMs）通过谐波减速器驱动.

轨迹跟踪任务是工业自动化与控制领域经常遇到的问题.轨迹跟踪控制一般分为两种，一种是通过控制策略来实现，主要处理跟踪中的非线性、不确定性和跟踪误差等干扰，目前，比较常见的有鲁棒控制［6-7］、模型预测控制（Model Predictive Control，MPC）［8-10］、滑模控制（Sliding Mode Control，SMC）［11-12］和自适应控制［13-15］等智能控制算法.另一种是通过施加物理约束实现，也就是将期望的运动轨迹通过合适的物理结构设计来达到.本文采用的方法是这两种方法的结合，将运动轨迹需求作为约束对待，但这个约束不是来自环境，而是在机械系统动力学的框架下计算相应的约束力，并通过控制系统施加这个需要的约束力来实现，称其为约束跟随理论.

动力学建模与控制是机械系统最传统的研究方向，在众多的动力学建模方法中，基于Udwadia-Kalaba 方程［16］的建模方法的提出是近一个世纪以来动力学建模方向非常重要的进展.相比之下，该方法不出现任何辅助变量（如拉格朗日乘数）或伪变量（如广义速度），可以求得满足高斯最小原理和达朗贝尔原理的约束解析解，即可以得到封闭形式的解.该优势可用于建模与控制领域，如最优跟踪控制［17］、动态建模［18］、家用智能车控制［19］、车辆运动控制［20］、列车虚拟联挂控制［21］等.

根据这一点，基于Udwadia-Kalaba 方程，将期望轨迹作为约束条件引入约束跟随控制方法［22-24］，这里的约束不是真实的，而是虚拟的.与传统的跟踪控制相似，Chen［25］研究了机械系统稳定与最优设计中的约束跟随伺服控制.Zhao 等［26］将该方法应用于人工蚁群跟踪控制.对于具有不确定性的机械系统，Chen 和Zhang［27］提出了一种自适应鲁棒近似约束跟随方法.

本文提出一种基于Udwadia-Kalaba 方程的约束跟随理论来实现云台水枪喷嘴的跟踪控制问题.将消防无人机下固定的云台装置驱动的水枪喷嘴运动轨迹作为需要跟随的约束，利用Udwadia-Kalaba 方程得到实现该跟随约束所需的实时驱动力.在此基础上，建立水枪喷嘴运动轨迹跟踪控制方法.利用Adams 软件建立云台系统的物理模型，并在MATLAB/Simulink 环境下编制控制算法，通过联合仿真验证了该方法的有效性.同时，针对实际应用中的云台系统，设计了一种基于数字信号处理器（Digital Signal Processor，DSP）的驱动与控制集成系统，利用两台BLDCMs 对系统进行驱动.仿真和实验验证了该方法的有效性和实用性.

1 云台水枪喷嘴驱动结构设计

1.1 水枪喷嘴运动需求

如图1 所示，安装在UAV 下的云台装置可以驱动水枪喷嘴将水或灭火剂沿正确方向喷洒到着火点.在灭火作业中，高度方向的保持由UAV 自身高度保证，但要求水枪喷嘴必须在一定范围内摆动，使水尽可能覆盖着火点.因此，水枪喷嘴驱动机构应满足相应的运动要求，即水平和垂直运动或两者组合运动.

图1 配有云台的消防UAVFig.1 Firefighting UAV with pan/tilt

采用两自由度云台装置分别实现横摆和俯仰运动，满足水枪喷嘴的运动要求.考虑到高层建筑消防的实际需要，横摆和俯仰的运动范围分别为±170°和±17°.通过运动组合，可以获得水枪喷嘴的期望轨迹，从而为实际灭火提供更加复杂的运动跟踪需求.

1.2 云台的结构

图2为云台结构，云台通过基座固定在UAV 下，通过横摆电机和俯仰电机实现水枪两个自由度的运动.两台BLDCMs 带动相应的谐波减速齿轮，两个谐波齿轮的减速比都是100.横摆电机和俯仰电机具有相同的结构和参数，其中电机额定功率均为100 W.此外，由于UAV 的负载限制，云台必须尽可能地减少其自身的重量.为此，该装置的主要元件采用PA6材料制造，该材料具有较好的机械强度、耐磨性、耐腐蚀性，且重量较轻.

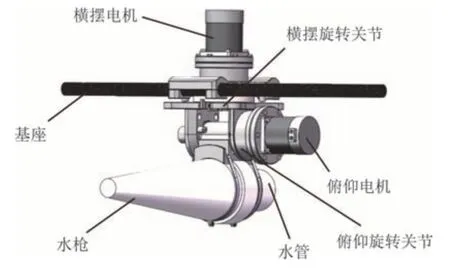
图2 云台结构Fig.2 The pan/tilt structure

2 系统建模

2.1 坐标系建立

描述系统的首要任务就是建立合适的坐标系.针对无人机云台的结构和运动特点，可以通过机器人技术中常用的Denavit-Hartenberg（D-H）方法来实现，即将该系统视为两自由度的机械臂，建立的连杆坐标系如图3 所示.横摆电机驱动的运动部件称为横摆运动部件，俯仰电机驱动的运动部件称为俯仰运动部件.如前面所述，云台系统有两个转动关节，分别是横摆关节和俯仰关节.

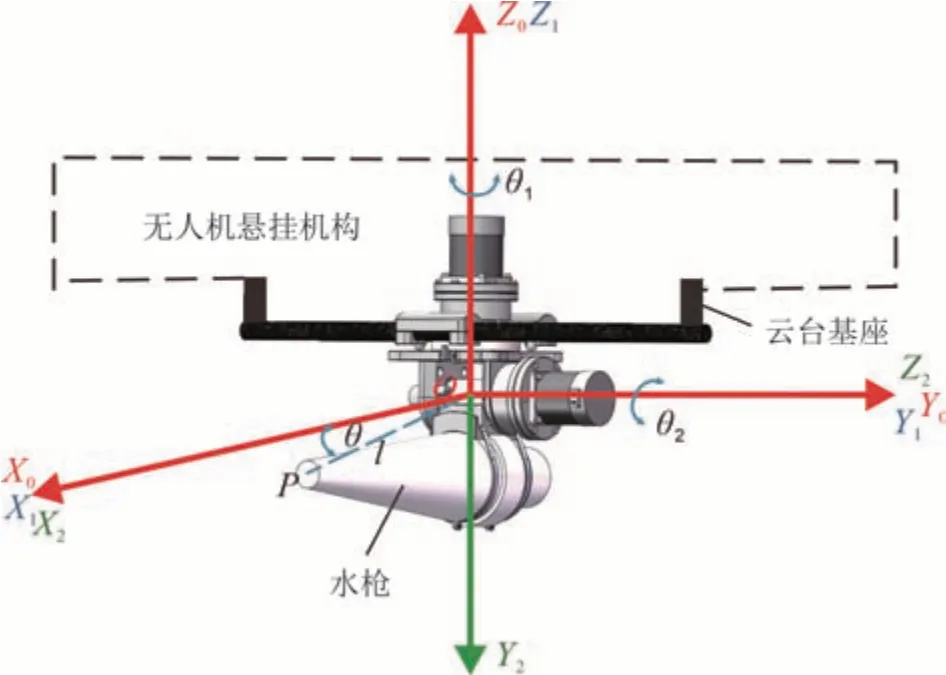
图3 云台坐标系Fig.3 Coordinate systems of pan/tilt

横摆和俯仰运动部件的质量分别为m1和m2.由此建立了三种坐标系：基坐标系O-X0Y0Z0，横摆坐标系O-X1Y1Z1、俯仰坐标系O-X2Y2Z2.由于两个转动关节的轴线相互垂直并相交，因此，根据经验选择模型的三个坐标系的原点重合并固定在俯仰关节的中心位置.轴Z1和轴Z2的方向分别是横摆关节轴和俯仰关节轴的方向，X0、X1、X2轴方向为水枪喷嘴方向，轴Y0、Y1、Y2的方向是根据右手定则确定的.P是水枪喷嘴的末端，l为线段OP的长度，θ为线段OP与水枪所在直线之间的夹角，且l和θ均为常值.

2.2 运动学方程

云台的连杆参数如表1所示.

由坐标变换关系，可以得到不同坐标系之间的变换矩阵.基坐标系0到俯仰坐标系2的变换矩阵可以表示为：

式中：s1=sinθ1，s2=sinθ2，c1=cosθ1，c2=cosθ2；θ1是横摆关节的旋转角；θ2是俯仰关节的旋转角.

由图3 可知，水枪喷嘴末端P相对于坐标系2 即俯仰坐标系的坐标为2P=[lcosθlsinθ0]T，相对于云台基坐标系的坐标为0P.假设在基坐标系下0P=[xyz]T，那么

因此，由关节变量描述的水枪喷嘴末端P相对于基坐标系的坐标可以表示为：

式中：l为线段OP的长度；cθ=cosθ；sθ=sinθ.

至此完成了云台系统运动学方程的建立，为后续的伺服约束控制提供数学基础.由式（3）的逆解可得：

3 机械系统约束跟随

3.1 受约束的机械系统

考虑一个无约束的机械系统［28］

式中：t∈R是独立变量时间；q∈Rn是广义位置坐标；∈Rn 是广义速 度；∈Rn是广义加速度；M(q，t) ∈Rn×n是对称正定惯性矩阵（在某些特殊情况下，其正定性并不总是正确的［29］，本文不考虑这种特殊情况）；Q(q，t) ∈Rn是沿着广义坐标的广义外力，包括重力、离心力以及控制输入等.

假设系统（5）受以下m个约束

式中：φ(⋅)：Rn×Rn×R→R，φ(⋅)是光滑的.

需要指出的是，系统（5）所受的约束（6）除了物理约束，也可能是运动轨迹约束或者其他性能要求等虚拟约束.由于初始时刻偏差、数值计算误差等影响，等式约束（6）有可能不成立，为了使得式（6）在一定的时间内收敛，约束（6）可以等效表示为［30］：

式中：μi为正实数，i=1，2，…，m.

将式（8）代入式（7）得：

将约束（7）用矩阵形式表示为：

约束（6）可能是完整约束或非完整约束.这里，我们指出满足约束的所有q和都包含在集合q∈Ψ⊆Rn，∈Ω⊆Rn中.为了方便，我们将约束（10）表示为：

式 中：A(q，，t) ∈Rm×n被称为约束矩阵；b(q，，t) ∈Rm是一个m× 1维向量.

式（11）是约束的二阶表示形式，是进一步进行动力学分析与控制设计的最优形式.Chen［25］认为各种控制问题，如轨迹跟踪、稳定性、最优控制等都可以把约束表示成式（11）的形式.对于给定的A和b，如果式（11）至少存在一个解，则称约束（11）是一致的，本文假设约束（11）是一致的.约束（11）一致的充分必要条件为AA+b=b，其中A+表示A的Moore-Penrose 广义逆矩阵.约束（11）的一致性假设的含义说明了这些期望约束是符合实际并不是互相矛盾的.

3.2 约束跟随控制理论

具有约束的机械系统运动问题可以转化为系统的轨迹跟踪问题［31］，即在轨迹跟踪控制问题中，区别于物理约束，可以把期望轨迹当作是一种无形的虚拟约束，如果用伺服控制的方式来实现，称它为伺服约束.也就是说问题变为，求解满足轨迹跟踪控制所需要的控制力，保证系统（5）满足约束（11），这就是约束跟随控制问题.

根据牛顿力学，只有力才能改变机械系统的运动状态.因此，要满足轨迹跟踪约束式（11），可以把受约束的机械系统写为：

式中：Qc(q，，t) ∈Rn是系统（5）满足约束（11）时所必须施加的伺服约束力.

根据达朗贝尔原理的拉格朗日形式，无约束系统（5）满足约束（11）时所需要的伺服约束力Qc的解析形式为［16］：

式中：上标“+”表示Moore-Penrose 广义逆；a=M-1Q表示无约束系统在t时刻的加速度.

联立式（12）和式（13），得到受约束机械系统的动力学方程为：

方程（14）也被称为Udwadia-Kalaba 方程，它是进行动力学建模与控制的一种力学理论基础.显然，从Udwadia-Kalaba 方程可以封闭解的形式来描述约束力学系统，而不需要引入拉格朗日乘数等伪变量.控制运动的约束力可以通过式（13）得到.因此，Udwadia-Kalaba 方程可以用于伺服控制.将系统运动轨迹作为期望约束（约束跟随），跟踪控制的目的是找到合适的约束力来引导系统沿期望轨迹运动.

4 云台水枪喷嘴轨迹跟踪控制

4.1 无约束系统运动方程

基于约束跟随控制理论的框架，无约束系统是指系统没有考虑控制，即没有轨迹运动要求的系统.根据图3，将θ1和θ2作为广义坐标，分别记为q1和q2.利用拉格朗日方程得到无约束条件下的云台系统的动力学方程

式中：x1c、y1c表示横摆运动部件质心位置在坐标系O-X1Y1Z1上的分量；x2c、y2c表示俯仰运动部件质心位置在坐标系O-X2Y2Z2上的分量；I1zz表示横摆运动部件绕旋转轴的转动惯量；I2xx、I2yy分别表示俯仰运动部件绕其相应轴的转动惯量；s1=sinθ1，s2=sinθ2，c1=cosθ1，c2=cosθ2；θ1是横摆关节的旋转角，θ2是俯仰关节的旋转角；m1、m2分别表示横摆和俯仰运动部件的质量；g表示重力加速度.

4.2 云台运动约束条件

对于无约束云台系统（15），要求其喷嘴实现期望的运动轨迹，该系统成为一个有约束机械系统.如前述，为实现这个期望约束，应增加额外的伺服约束力.这里将云台水枪喷嘴末端的运动轨迹作为需要施加的约束条件.

由于云台系统只有横摆和俯仰2 个自由度的运动，故目标轨迹只对y、z方向上的位置有约束，对x方向并无要求.假设选取云台系统的水枪喷嘴末端目标运动轨迹为y-z平面上半径为0.06 m、圆心为（0，-0.09）的圆.若选取关节角速度为2 rad/s，则采用下列方程组描述云台系统的轨迹约束方程：

根据以上讨论，结合式（3），轨迹约束为：

式（17）对时间t求一阶和二阶导数，约束方程可以写成式（11）的形式，其相关项A、b分别为：

4.3 伺服约束力求解

如图4所示是求解伺服约束力的过程.针对无约束系统，如前所述，首先给出一组期望轨迹（约束方程）.为了解决初始误差和计算误差等原因可能产生的偏差，对约束采用渐进收敛（稳定）处理，并把它写为式（11）的形式.为实现期望的运动轨迹（虚拟约束）要求，需要在无约束系统上增加额外的力或力矩，即伺服约束力，使系统沿期望轨迹（约束）运动.在此基础上，根据式（13）计算伺服约束力的解析解，显然这个伺服约束力随着系统状态的变化而在不断变化.

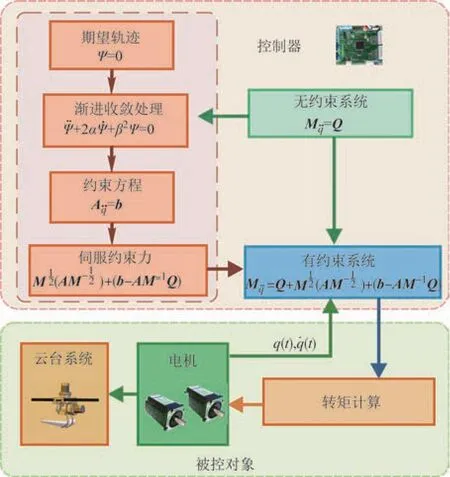
图4 伺服约束力求解Fig.4 Solution of servo constraint force

为了满足水枪喷嘴运动轨迹的要求，即需要的约束条件，根据式（13）可以得到施加在电机上的控制力矩：

式中：τ=τ1、τ2分别表示横摆关节和俯仰关节处所需要施加的伺服力矩.

5 轨迹跟踪控制仿真

5.1 云台系统物理模型

仿真的目的是验证提出的约束跟随理论对水枪喷嘴进行跟踪控制的有效性.在式（18）得到的力矩下，水枪喷嘴末端的运动轨迹将是期望轨迹.此外，在进行物理实验之前，从安全性和成本的角度对所提出的方法进行模拟也是有必要的.

由图4 可知，作为控制对象，需要得到云台系统的物理模型，才能完成仿真.采用 SolidWorks 软件建立云台系统三维模型并将其导入Adams 环境中，如图5 所示.利用 Adams 模型还可以得到其位移、速度和加速度等物理参数.

图5 云台的Adams模型Fig.5 Adams model of the pan/tilt

5.2 约束跟随的稳定性处理

约束跟随理论基于系统模型和初始条件.根据系统模型和运动状态，连续计算引导水枪喷嘴沿期望轨迹运动的力矩（18）.由于数字误差、建模偏差、初始条件不相容、外界干扰等原因，跟踪误差不可避免.为了稳定约束跟随，采用Baumgarte 约束违约稳定法［32-33］.也就是说，在加速度约束方程中加入位移和速度约束，将不稳定的二阶约束方程=0 变为稳定的约束方程

式中：α，β是正常数，分别作为二阶阻尼系统的阻尼系数和刚度.随着时间的推移，Ψ中的约束将收敛到零并满足式（11）.

实际上，考虑约束（11），在这种情况下，相比于不稳定的方法，在稳定过程中除了b外，没有改变系统参数来处理跟踪控制，即稳定后，A与前面相同，而b不同，用b'代替.

5.3 相容初始条件下的仿真

在初始时刻，如果期望轨迹中给定的初始位置和速度与系统实际是一致的，则称为相容初始条件.在这种情况下，初始点刚好在期望轨迹上.

根据2.2节的运动学逆解，取相容初始条件为：

将Adams 模型导入Matlab/Simulink 仿真环境中，在MATLAB/Simulink 下进行仿真.在Matlab 中设置相关参数，并将初始条件（20）和控制（18）应用到从Adams 导入的云台模型上，仿真时间为10 s.水枪喷嘴末端期望轨迹在相容初始条件下的仿真结果如图6和图7所示.

图6 相容初始条件下的跟踪控制Fig.6 Tracking control with consistent initial conditions

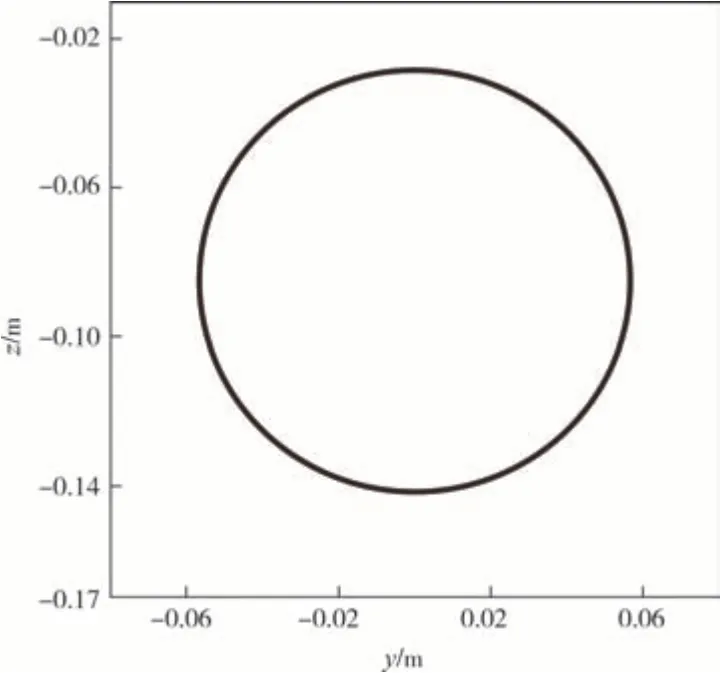
图7 相容初始条件下y-z平面上的运动轨迹Fig.7 Motion trajectory in y-z plane with consistent initial conditions

图6（a）、图6（b）分别为在横摆和俯仰关节施加的力矩，图6（c）、图6（d）分别为横摆和俯仰关节的角度位置，图6（e）、图6（f）分别为水枪喷嘴末端在y、z方向上的误差，图7为相容初始条件下的运动轨迹.

由图6 和图7 可以看出，云台水枪喷嘴在y-z平面上的轨迹为半径为0.06 m、圆心为（0，-0.09）的圆，与预期一致.但是从图6（e）和图6（f）可以看出，误差范围在0～0.8 s.产生这种误差的原因是建模偏差，由于采用了上述的稳定方法，误差会随着时间的推移收敛到零.

5.4 不相容初始条件下的仿真

基于Udwadia-Kalaba 方程的约束跟随控制方法不适用于初始条件不相容的情况，即系统的初始位置或初始速度不在期望轨迹上，与系统不匹配.用Baumgarte 约束违约稳定法来修正这个不相容引起的偏差.

为了说明稳定的适用性，假设给定不相容初始条件为：

仿真时间为10 s，该工况的跟踪控制仿真结果如图8、图9所示.

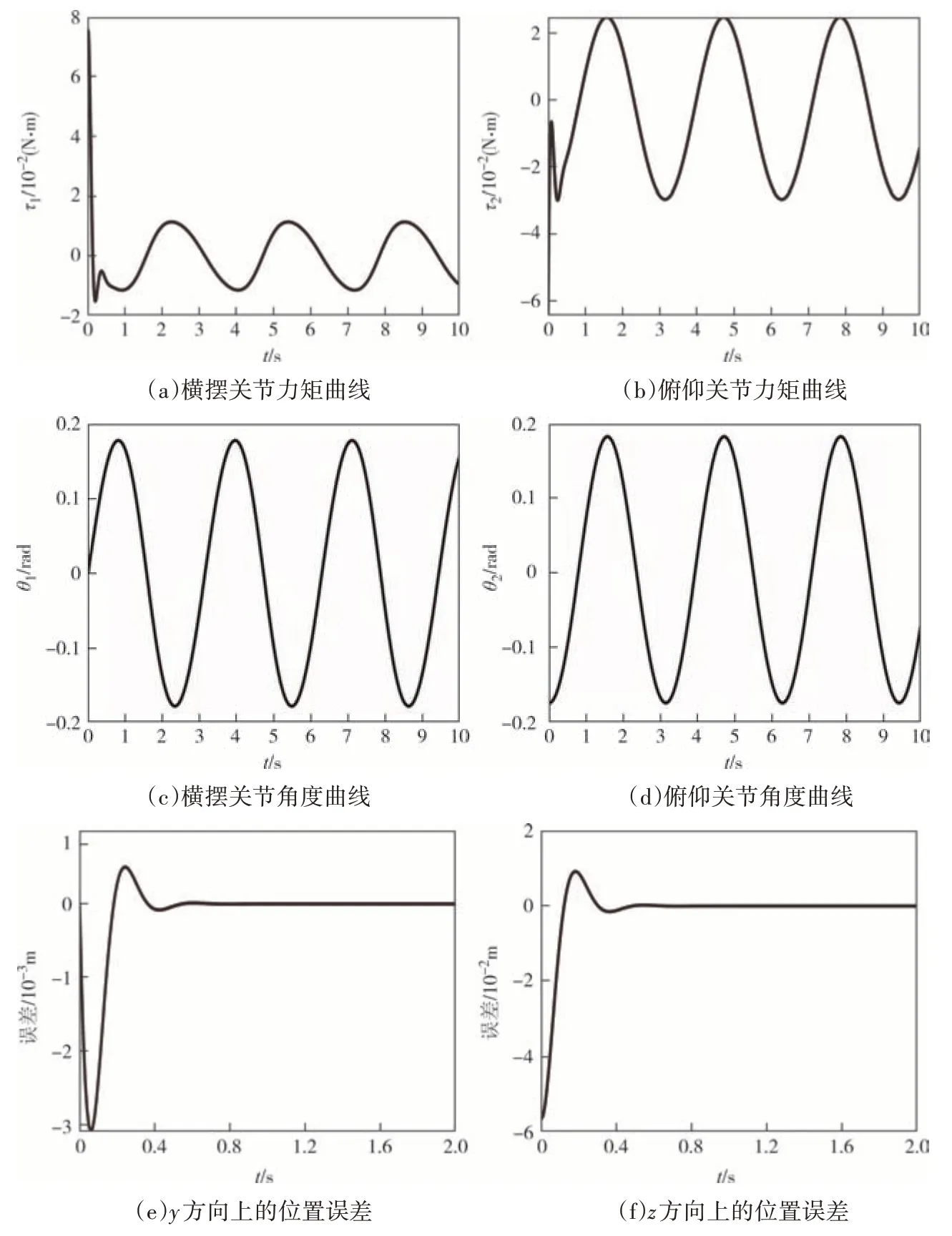
图8 不相容初始条件下的跟踪控制Fig.8 Tracking control with inconsistent initial conditions

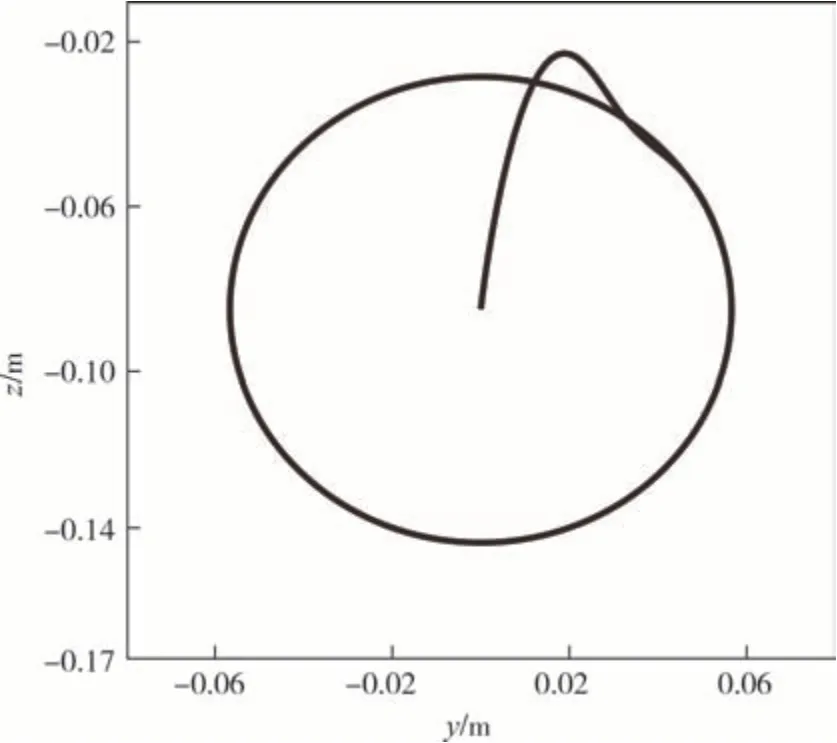
图9 不相容初始条件下y-z平面上的运动轨迹Fig.9 Motion trajectory in y-z plane with inconsistent initial conditions

图8（a）和图8（b）分别表示了横摆和俯仰关节的力矩，图8（c）和图8（d）分别表示了横摆和俯仰关节的角度位置，图8（e）和图8（f）分别表示了水枪喷嘴末端在y和z方向上的误差，图9 为不相容初始条件下的运动轨迹.

由于初始条件不相容，即初始位置和速度不在期望轨迹内，初始阶段的误差相对较大.但在约束违约稳定下，跟踪误差逐渐减小并趋近于零，即跟踪控制是有效的.

6 实 验

6.1 实验目的

仿真结果表明，本文提出的约束跟随控制方法用于由云台装置驱动的水枪喷嘴运动轨迹跟踪控制具有很好的效果.在仿真中，采用了基于Adams 的系统模型和基于Matlab/Simulink 的仿真环境.为了进一步验证约束跟随理论的有效性，需要在实际的物理系统和控制器上进行实验.为了与仿真有更好的对比，水枪喷嘴的期望轨迹采用和仿真同样的要求［式（16）］.

6.2 实验设备

搭建以TI TMS320F28069 DSP 控制器为核心的实验平台，通过两台无刷直流电机驱动云台装置，实验所需的控制结构如图10 所示.无刷直流电机具有成本低的优点，但是位置控制精度较低.在此实验中，电机转角参数采用嵌入电机中的霍尔位置传感器来得到，并通过微分得到角速度.实验中采用了电机控制算法的磁场定向控制（Field Oriented Control，FOC）.

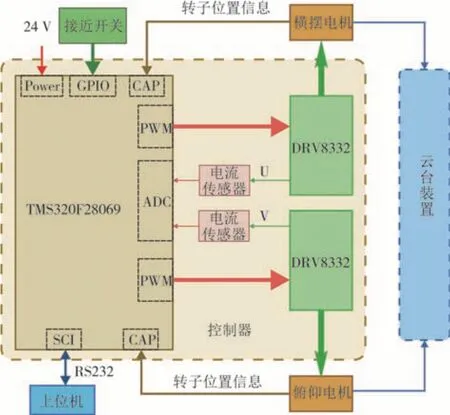
图10 实验结构Fig.10 Experiment structure

根据式（18）对算法进行编程，在PC 上结合Matlab/Simulink 和C 语言，通过自动代码生成技术将控制算法编译并加载到DSP 控制器中.需要指出的是，我们使用了上面介绍的稳定方法，即在式（18）用b'代替b.

控制器输出的驱动电机的电流与所需转矩成正比，由两台电机驱动云台使得水枪喷嘴运动，实验设备如图11所示.

图11 实验设备Fig.11 Experiment equipment

实验结果及与仿真结果的对比如图12 所示，分别为水枪喷嘴的横摆角、俯仰角和水枪喷嘴末端的轨迹，实验结果与仿真结果的吻合度较好.

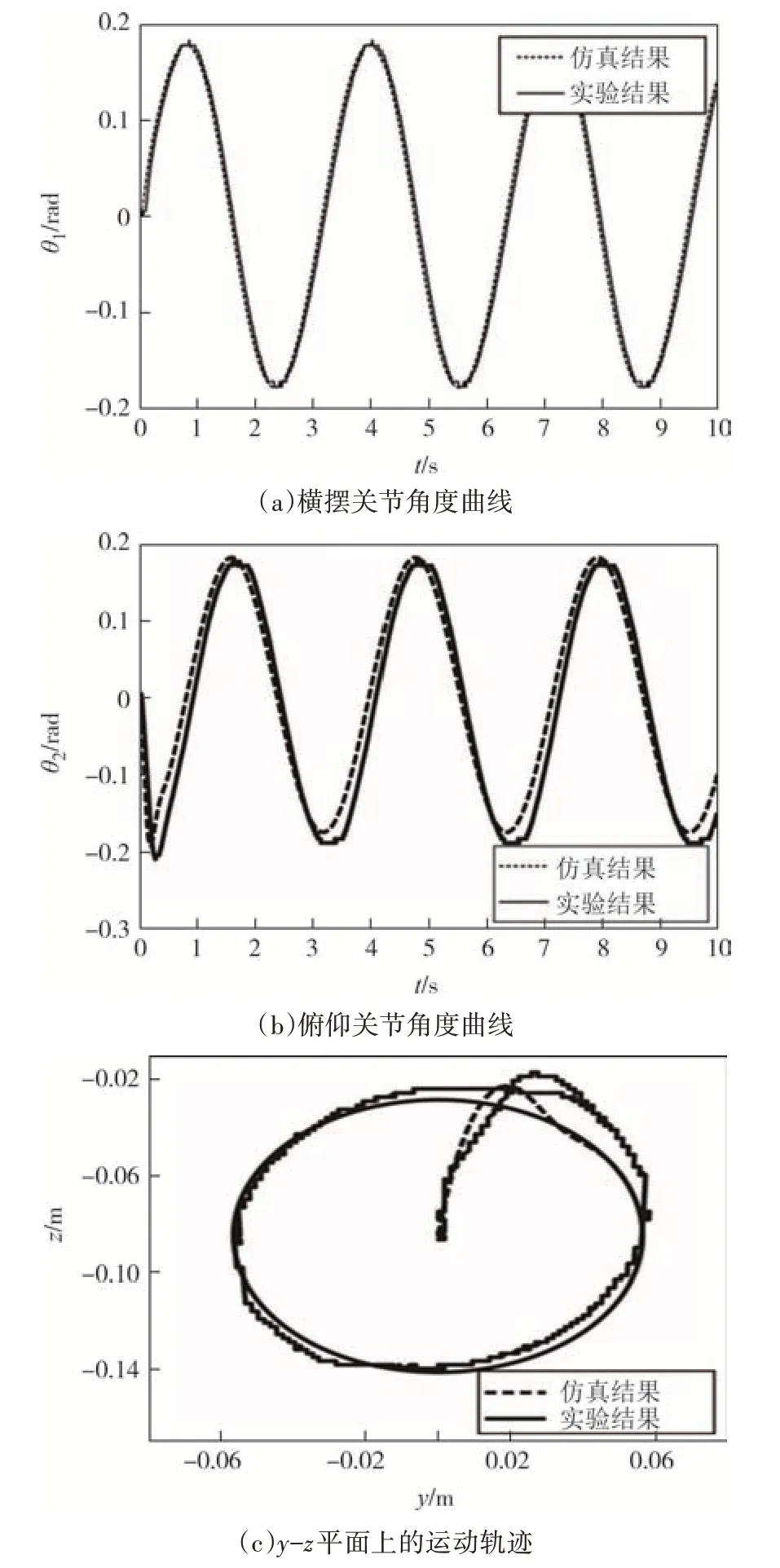
图12 水枪喷嘴末端跟踪轨迹的比较Fig.12 Tracking trajectory comparison of water-jet nozzle end point

水枪喷嘴末端在y方向和z方向上实验轨迹与期望轨迹的误差如图13所示.

水枪喷嘴末端跟踪轨迹与预期基本吻合，但仍存在一定误差，造成这种误差的原因主要是：

1）约束跟随跟踪控制依赖于机械系统的建模精度，不可避免地存在参数误差，如质量、质心、惯性矩等，从而导致建模偏差.

2）角度测量误差.角位置和角速度在控制转矩计算中非常重要，在云台控制系统中，由于成本原因，没有使用编码器，由BLDCMs 所带的霍尔传感器来测量关节角度.根据BLDCMs 的特点可知，该传感器的输出信号存在一个扇区误差（60°电角度），使得实验结果存在一定的偏差.

针对消防无人机的实际需求，从实验结果可以看出，水枪喷嘴运动误差在允许范围内，所采用的控制方法对云台喷嘴运动轨迹的跟踪控制是可行的.

7 结论

本文提出一种约束跟随方法研究了无人机下固定的驱动水枪喷嘴运动的云台跟踪控制问题.该控制理论基于Udwadia-Kalaba 方程，约束跟随方法没有对被控对象进行线性化处理，也没有引入伪变量或其他算子来得到控制，该方法可以直接得到控制的封闭解析解.针对消防无人机水枪喷嘴运动控制的要求，以水枪喷嘴的期望运动轨迹为约束条件，计算水枪喷嘴驱动电机所需的力矩.该方法所得到的力矩为封闭形式，这是约束跟随控制的优点之一.仿真和实验结果表明，采用基于约束跟随的跟踪方法对消防无人机云台装置进行运动控制是有效的.在实际应用过程中，由于外部扰动以及建模误差等影响，很难获得无人机云台的准确模型，所以无人机云台系统存在不确定性且是未知的.因此，在设计控制输入时考虑无人机云台系统的不确定性需要在今后的工作中完成.