干气密封端面型槽可控激光制备的参数模型及实验验证

王衍 ，孔康杰 ，何一鸣 ，王英尧 ，刘永振 ，赵全忠

（1.江苏海洋大学 机械工程学院，江苏 连云港 222005；2.南京萃智激光应用技术研究院有限公司，江苏 南京 210034）

干气密封是一种动压型非接触式密封［1-2］，主要解决了机械密封的干运转难题，凭借零泄漏、无磨损、低能耗等优势在石油、冶金和化工领域逐渐取代传统接触式机械密封［3］.干气密封区别于传统机械密封的关键技术特征是需在密封端面开设微米级动压槽型［4］，使旋转气体能够在微米级槽深的引导下实现定向增压.如何通过加工工艺实现介观槽深和槽底粗糙度的精确控制，直接影响干气密封的现场运行效果［5-7］.而且，实现一定工况下的既定最优槽深是干气密封理论研究对实际应用的具体指导和要求.对干气密封粗糙度的精准控制，一方面，源于微米级槽深本身已属于介观尺度，当粗糙度与槽深处于相近量级时将使目标槽深的定义失去意义；另一方面，多数情况下粗糙度对密封性能是有较大影响的.研究表明［8-9］：在相同工况和表面综合均方根差的条件下，粗糙表面的干气密封开启力、气膜刚度和摩擦扭矩均大于光滑表面；槽底面和软环密封端面的表面粗糙度对干气密封的性能具有较大影响.

Etsion 等［10-11］于1996 年提出微孔织构化端面密封技术，并于1999 年成功将激光雕刻技术应用于多孔端面机械密封的加工，显著提升了机械密封的使用寿命.Chichkov 等［12］于1996 年研究了飞秒、皮秒、纳秒激光的微观加工创面，认为激光加工的时间越短，激光烧蚀（Laser Ablation）在加工过程中的比重就越大，扩散（Diffusion）的比重越小，加工创面将越发平整、理想.盖晓晨［13］研究了飞秒激光的脉冲能量、扫描速度以及加工辅助气体对加工碳化硅（SiC）材料的影响，指出一定材料表面形貌下，降低扫描速度或增加脉冲能量都会提高材料的去除量，它们之间的关系呈非线性.毛文元等［14］基于纳秒激光加工技术，研究了给定深度和粗糙度指标下，工艺参数对碳化硅和碳化钨这两种材料上螺旋槽深度和粗糙度的影响，并通过正交实验，研究了各个参数的影响程度.2021年，毛文元等［15］进一步利用ACE非参数回归的方法建立了工艺参数与深度和粗糙度的关系，筛选出的参数基本可以达到兼顾加工效率和质量的要求.上述实验证明了采用离散编程方法可以实现对加工参数的优化，但尚未建立或深入探讨加工参数与加工现象的内在物理联系.

本文围绕干气密封槽型加工过程中的槽深和粗糙度两个关键指标，采用公式推导、编程模拟等方法，探讨光斑直径和填充间距对加工深度和粗糙度的影响，以期得到较为准确的加工参数-质量指标关系模型.与实验加工结果进行对比，建立最优参数的区间范围，完善基于材料气化阈值的激光精密加工思路，为干气密封高效精密制备提供理论基础.

1 理论模型

1.1 数学模型

结合实际加工情况，对加工模型作如下假设：1）光斑无衰减、加工创面理想；2）加工和检测设备有良好的重复定位精度、运动精度、振动稳定性；3）忽略数控操作延迟影响.

基于以上假设，激光加工过程中可以实现完全烧蚀，本文主要探究激光光斑直径、填充间距对密封环加工槽深及粗糙度的影响.根据相关文献［16］，单个光斑加工深度与激光器光斑能量、光斑直径及材料属性系数有关，为消除光斑能量和材料属性的影响，定义无量纲加工深度h*如下：

其中，A、B分别为与材料属性和激光器相关的变量，可以根据实验用激光器参数通过采用无量纲形式消除A、B的影响，无量纲基准值采用激光器标准值（光斑直径ds=15 μm，光斑间距S=15 μm）.

激光加工材料总去除量X为加工区域内光斑数量与单个光斑加工深度h*的乘积，规定一定范围内横向和纵向的光斑数量分别为m、n，则激光加工材料总去除量X可表示为：

定义光斑间距为S时，实际加工面积M为：

从而，开槽深度ha即为总去除量X与实际加工面积M的比值：

为考虑加工区域内所有激光光斑重叠情形，本文采用面积均方差（面粗糙度）Ras 评价槽区加工质量，建立面粗糙度理论模型.实际加工区域的主体是由若干个边长为一个填充间距S的正方形组成，图1所示为一个正方形加工区域内光斑重叠情况.

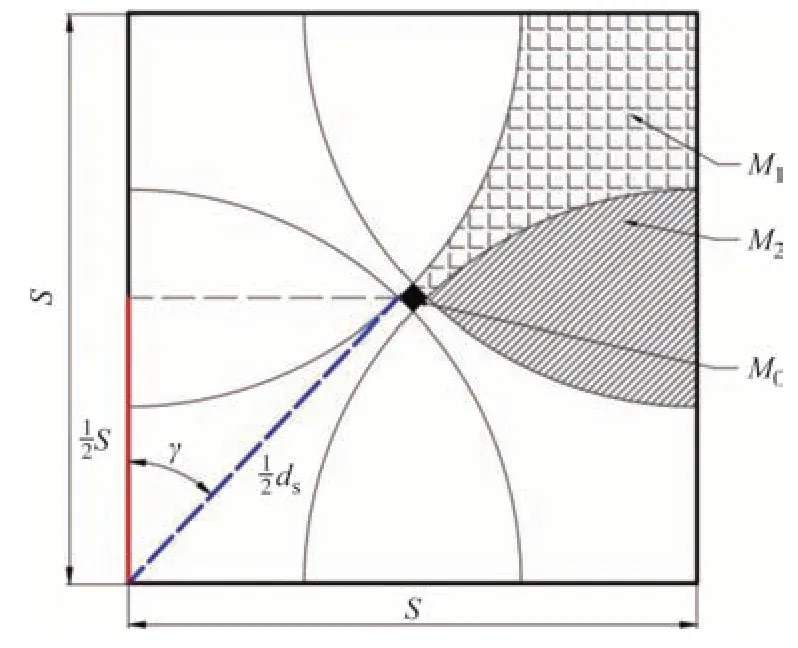
图1 光斑重叠区域示意图Fig.1 Diagram of spot overlap area

可以看出，此时的加工区域包含2h*（重叠2次）、h*（重叠1次）、0（无光斑）三种深度分布，对应的面积分别为M2、M1、M0：

基于以上分析，假设实际加工区域内包含的重叠次数为c1，c2，…，ci（ci为正整数），对应的加工深度可表示为c1h*、c2h*，…，cih*.通过对整个加工区域内相同重叠数汇总，建立面粗糙度Ras理论模型：

其中，Mi为与cih*对应的加工面积.

1.2 计算模型

当光斑间距过小且重叠次数过大时，正确分辨ci非常困难，直接应用上述模型进行实际问题的分析就显得十分繁琐，进一步合并统计Mi几乎无法完成.例如取光斑直径ds=15 μm、光斑间隔S=1 μm 时，此时加工区域内最大重叠次数可达174.鉴于此，可选择采用编程计算进行求解.

建立如图2 所示m=n=1 000 的单位长度数值模拟加工区域，区域面积由该区域内阵列点数量表示，即图示右上角洋红色圆形区域面积可由其包含的绿色阵列点数表示，据此可在程序计算中确定任意光斑位置和面积.

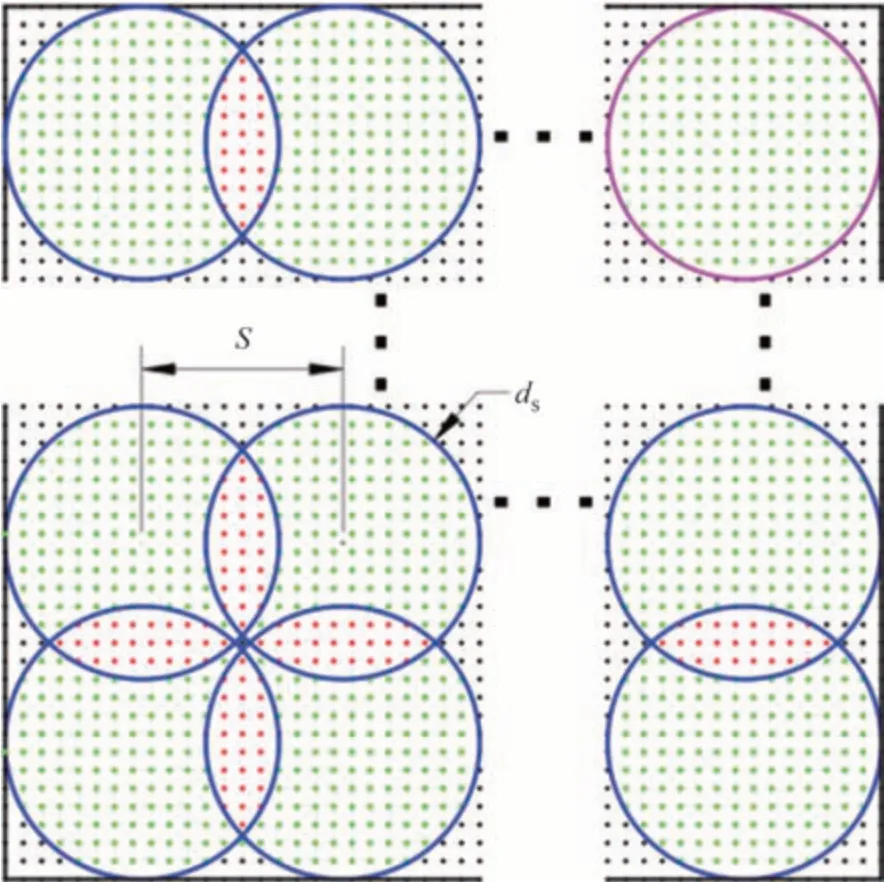
图2 光斑重叠示意图Fig.2 Diagram of spot overlap

采用Python软件对上述模型求解，取光斑直径ds=15 μm，记每个光斑加工深度为1 个单位深度，则每个阵列点对应的加工深度可由距该点距离小于ds/2的圆心数量决定.通过改变填充间距S研究加工深度变化规律，以图2 为例，黑色阵列点表示任何光斑的圆心距离该点都大于ds/2，绿色阵列点表示仅存在一个光斑满足圆心距离该点小于ds/2，红色阵列点表示满足条件的光斑数量为两个，以此类推.根据实际加工特点，圆心位于模拟加工区域内即被视为有效圆心，编程计算流程图如图3所示.

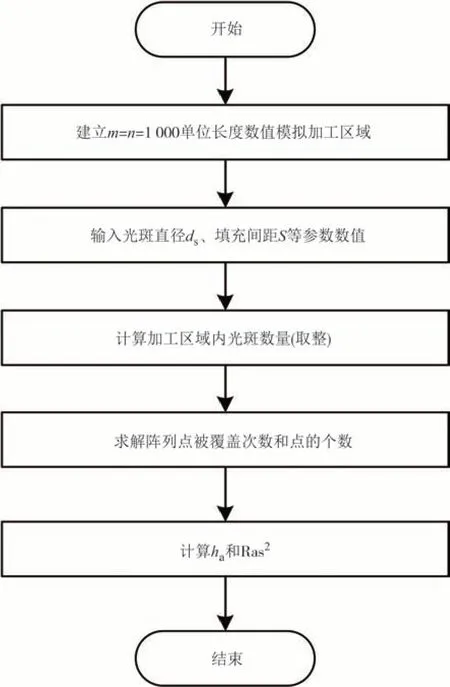
图3 计算模型流程图Fig.3 Flow chart of calculation model

2 数值模拟

2.1 填充间距的影响

实验研究表明［17］，当填充间距S超过光斑直径ds时，会出现不连续加工现象，为保证分析研究对应的实际加工具有良好的连续性，取填充间距小于光斑直径进行分析.

图4 所示为填充间距S变化对数值模拟槽深ha1和面粗糙度Ras1的影响规律图，由图4 可以看出，槽深ha1和面粗糙度Ras1随填充间距的变化规律非常相似，整体都是随填充间距的增大呈下降趋势.在S＜7 μm 区间，槽深和粗糙度受填充间距影响非常显著，随着填充间距的增大（S≥7 μm 以后），二者基本呈缓慢降低的变化趋势.

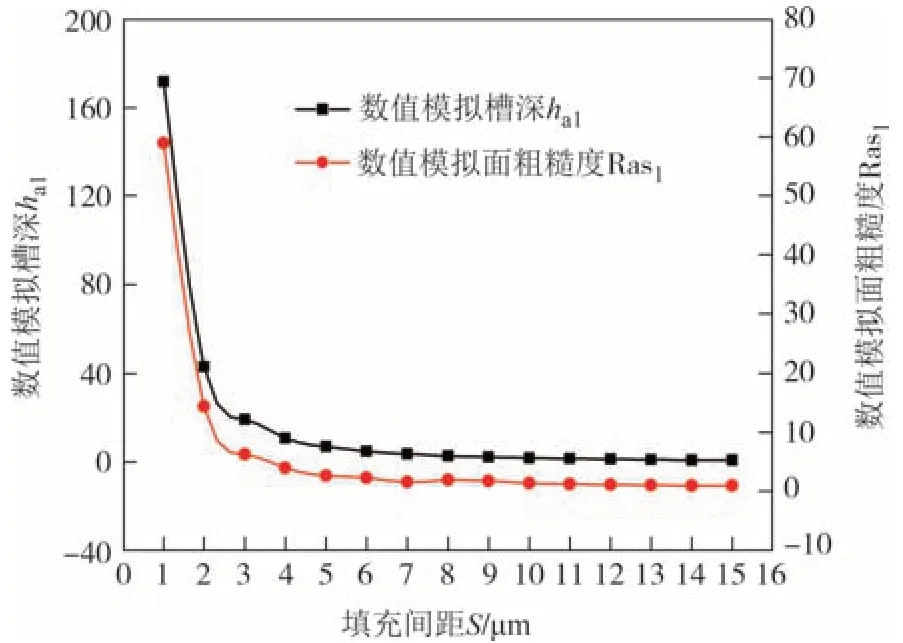
图4 无量纲槽深和面粗糙度随填充间距模拟计算（ds=15 μm）Fig.4 Simulated calculation of dimensionless groove depth and surface roughness with filling spacing（ds=15 μm）

2.2 光斑直径的影响

图5 所示为光斑直径ds变化对数值模拟槽深ha1和面粗糙度Ras1的影响规律图，由图可以看出，面粗糙度受光斑直径的影响较大，随着光斑直径的增大，面粗糙度呈先缓慢增大后迅速升高的趋势，临界分界点约在ds=7 μm.与面粗糙度表现不同，槽深受光斑直径的影响不显著，基本随光斑直径的增大呈小幅度的缓慢下降趋势.

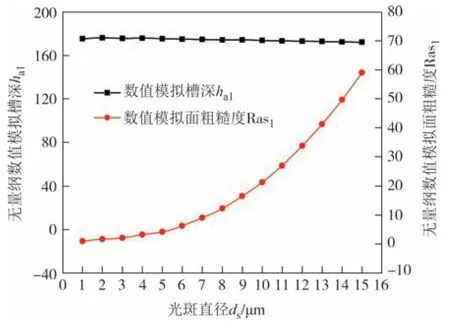
图5 无量纲槽深和面粗糙度随光斑直径模拟计算（S=1 μm）Fig.5 Simulated calculation of dimensionless groove depth and surface roughness with spot diameter（S=1 μm）

3 实验加工及验证

3.1 试件及实验条件

激光加工设备采用南京惠镭光电科技有限公司研制的HL-M7-20-V 型号光纤激光打标机，激光加工平台如图6 所示，可以实现对加工功率、光斑直径、填充间距、加工速度、重复频率等工艺参数的调节；检测设备采用陕西威尔机电科技有限公司研制的SPR2002N型粗糙度轮廓仪，轮廓仪测量线性精度最高可达0.8 μm，粗糙度测量线性精度最高可达5 nm，可以完成样品槽深和粗糙度的检测.实验密封环选用反应烧结碳化硅（SiC）材质，以2 mm×2 mm 正方形结构进行加工实验，加工样品如图7 所示.参数设置如表1所示，实验主要探究开槽深度ha和粗糙度Ras随光斑直径和填充间距的变化规律，并正与模型进行对比.

表1 加工参数Tab.1 Processing parameters

图6 激光加工平台Fig.6 Laser processing bench

图7 密封样品图Fig.7 Diagram of seal samples

3.2 激光加工与测量

3.2.1 实验加工

实验前，采用蘸了75%酒精溶液的无尘布将试件清洁后放置于工作台上；实验过程中，调节激光使其聚焦于试件表面，按照表1 所示参数进行加工，全程佩戴一次性手套.实验后，用含有75%酒精溶液喷雾器清洗实验加工槽并用无尘布擦拭干净.

3.2.2 样品测量

测量槽深的路径选择：以实验密封环光滑未加工面为基准面，深度探针运动路径的起点和终点均在基准面上，中间经过加工区域，且经过加工区域的长度不小于总路径长度的一半.按照该方法选择三条不重合的加工路径，测量结果为多次测试深度的平均值，记为ha2.测量粗糙度的路径选择：粗糙度探针运动路径始终在加工区域内，按照该方法同样选择三条不重合的路径，粗糙度仍取各条测试路径所得的平均值，记为Ras2.

在软件界面中，X轴为测针沿着工件滑行路径方向，Z轴为测针上下位移指示方向，由测针电学式长度传感器转换为电信号，然后经放大、滤波、计算后由软件显示出表面粗糙度数值.如图8 所示，槽深数值为实验测量平均深度，槽区上部直线为检测结果基准线，槽区底部直线为槽底加工表面粗糙度均值线，由图可以看出，密封环槽底整体加工质量良好.图9 所示为实验加工区域粗糙度检测结果图，由图可以看出，加工区域粗糙度整体也较均匀，峰值和谷值波动位于±1 μm以内，均匀度良好.

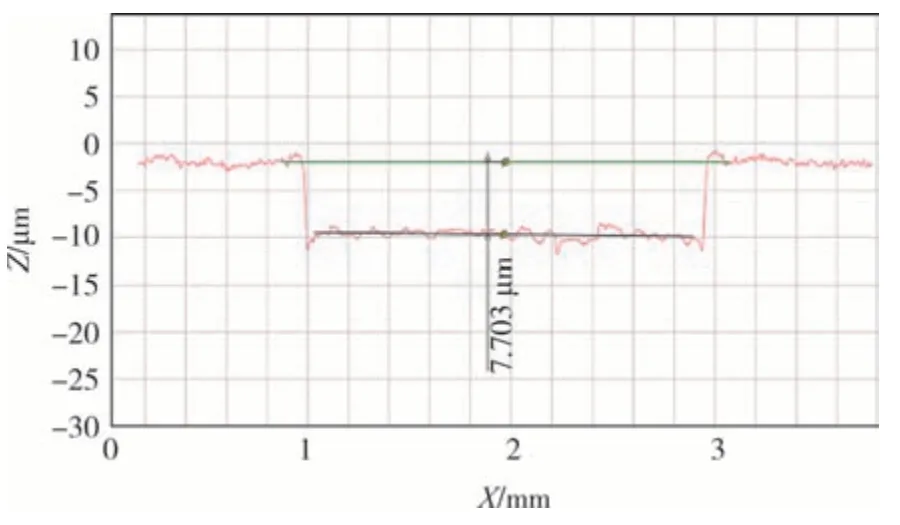
图8 实验槽深检测结果Fig.8 Experimental groove depth detection results

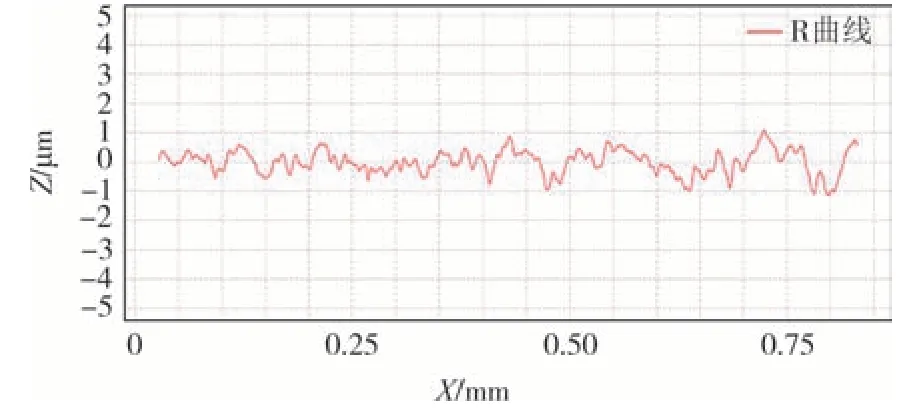
图9 实验粗糙度检测结果Fig.9 Experimental roughness detection results

3.3 实验结果与对比验证

为进行不同参数下数值模拟和实验加工槽深的对比，对数值和实验的相关数据进行归一化无量纲处理，可实现对计算结果的对比分析研究.

3.3.1 槽深结果对比

图10 所示为变填充间距S（S＜ds=15 μm）时模拟槽深ha1和加工槽深ha2的结果对比图.可以看出，实验加工槽深ha2随填充间距的变化规律与理论模型计算结果匹配较好，槽深的变化趋势与数值模拟结果基本一致，均随着填充间距的增大而减小，当S≥4 μm 时，实验加工槽深与数值模拟槽深数值之间的误差越来越小.

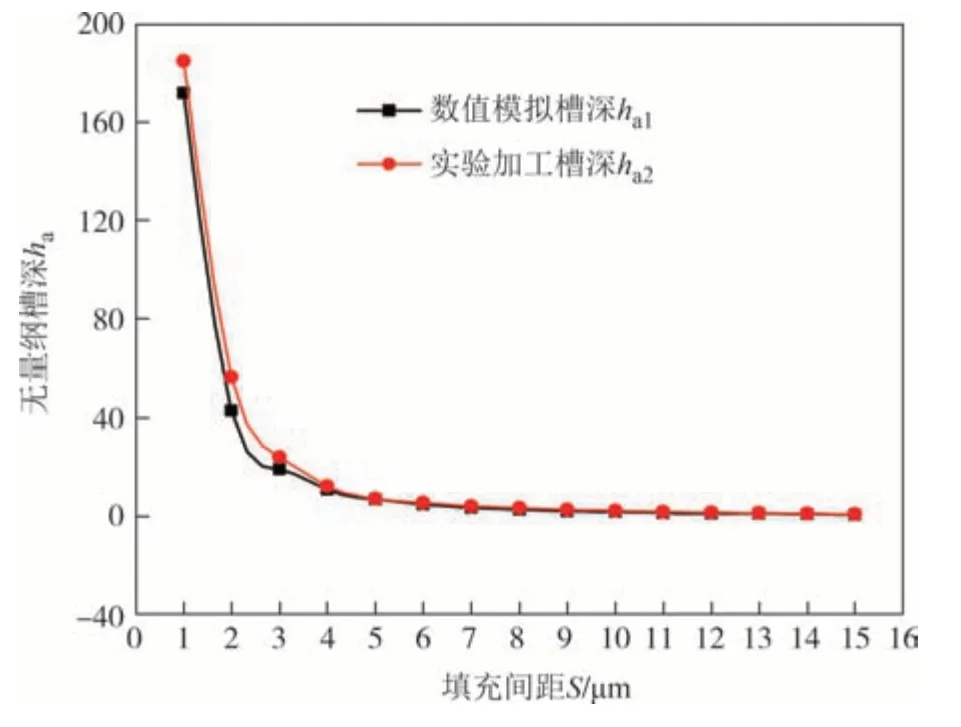
图10 变填充间距下无量纲实验槽深与模拟槽深对比（ds=15 μm）Fig.10 Comparison of the dimensionless experimental and simulated groove depths under varying filling spacing（ds=15 μm）

图11 所示为填充间距S=1 μm 时变光斑直径下实验槽深与模拟槽深结果对比图，可以看出，实验加工槽深ha2随光斑直径的变化规律为基本围绕理论模型计算结果上下波动，实际加工槽深受光斑直径变化的影响，呈现波动性变化，与理论结果符合较好.

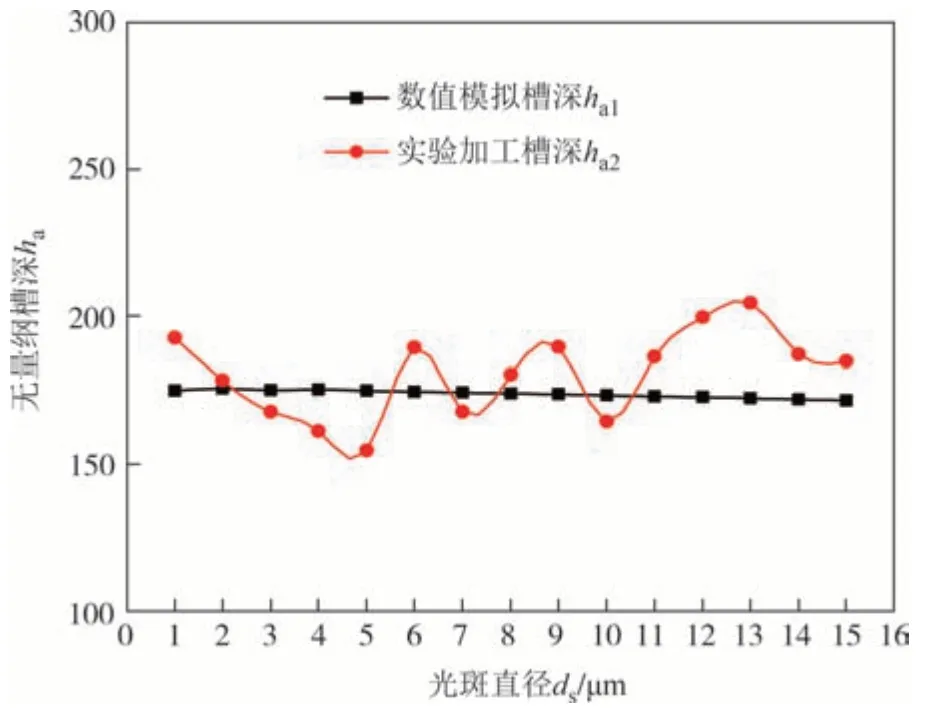
图11 变光斑直径下无量纲实验槽深与模拟槽深对比（S=1 μm）Fig.11 Comparison of the dimensionless experimental and simulated groove depths under variable spot diameter（S=1 μm）

加工槽深随光斑直径变化呈波动性变化，分析认为造成这种现象的原因：一方面是由于实际加工中光斑直径的变化会造成光斑能量的变化，二者相互作用产生部分抵消的效果，而在数值计算中没有考虑能量变化的影响；另一方面是由于实验样品表面本身具有一定的粗糙度，在数值计算中未考虑这方面的影响.

3.3.2 粗糙度结果对比

图12 所示为变填充间距S（S＜ds=15 μm）时模拟面粗糙度Ras1和加工面粗糙度Ras2的结果对比图.由图12 可以看出，当1 μm≤S≤3 μm 时，加工粗糙度与模拟粗糙度数值差距较大，但其变化趋势相似；当S≥4 μm 时，实验加工粗糙度随填充间距的变化规律与理论模型计算结果匹配较好，两者变化趋势基本一致，均随着填充间距的增大而减小.

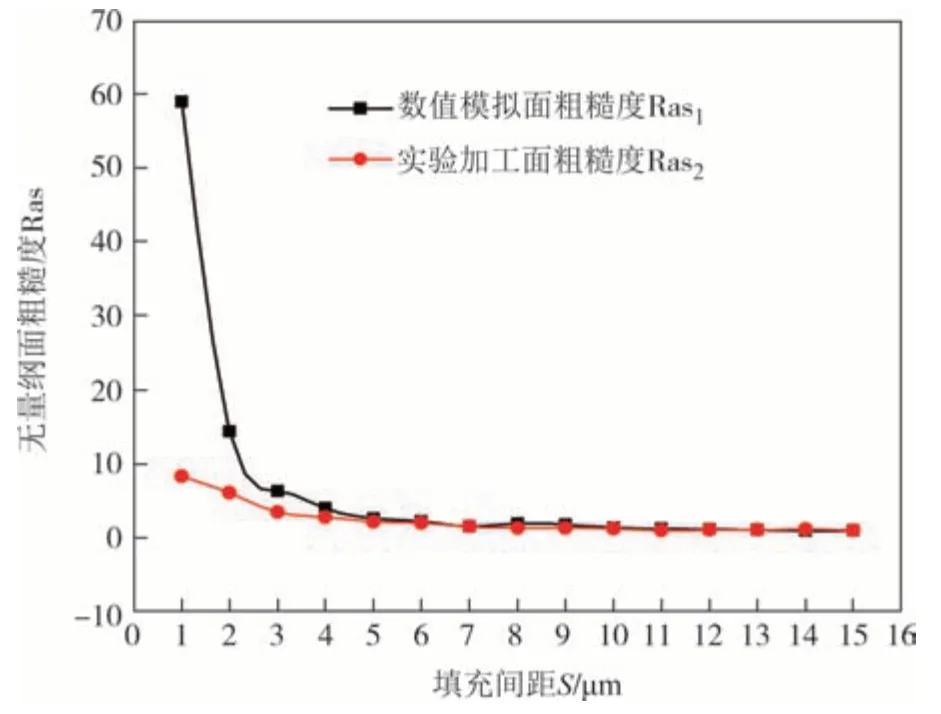
图12 变填充间距下无量纲实验粗糙度与模拟面粗糙度对比（ds=15 μm）Fig.12 Comparison of the dimensionless experimental and simulated surface roughness under varying filling spacing（ds=15 μm）

图13 所示为变光斑直径变化对数值模拟面粗糙度Ras1和实验加工面粗糙度Ras2结果对比图.可以看出，数值模拟粗糙度随着光斑直径的增大而增大，而实验加工粗糙度随光斑直径的增大在固定数值处呈现一定的波动变化，与数值模拟结果有较大差异.究其原因，除了实验样品表面自有粗糙度影响以外，还有两个因素：一是理论模型的不完善，二是加工实验中出现的熔融物扩散现象.

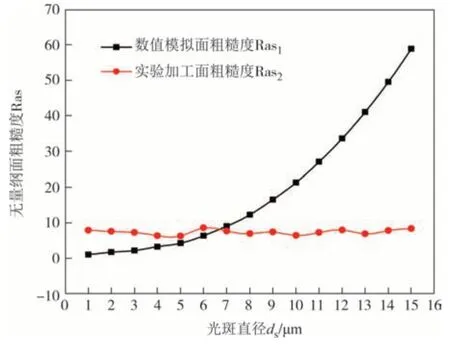
图13 变光斑直径下无量纲实验面粗糙度与模拟面粗糙度对比（S=1 μm）Fig.13 Comparison of the dimensionless experimental and simulated surface roughness under variable spot diameter（S=1 μm）

一方面，上文粗糙度理论模型通过统计计算区域内各深度分布的平方平均数，模拟加工区域边缘始终存在过渡加工区域，如图14 所示.过渡加工区分布于加工区域的四周，其深度差随填充间距的减小逐渐明显，并向内延伸约一个光斑直径的长度，在计算平均深度时因面积占比小而影响有限，但在计算粗糙度时，深度的均值差是按平方计算的，会进一步放大深度偏差的影响，造成粗糙度计算出现较大误差，进而造成模拟粗糙度大于实际测量粗糙度的现象.

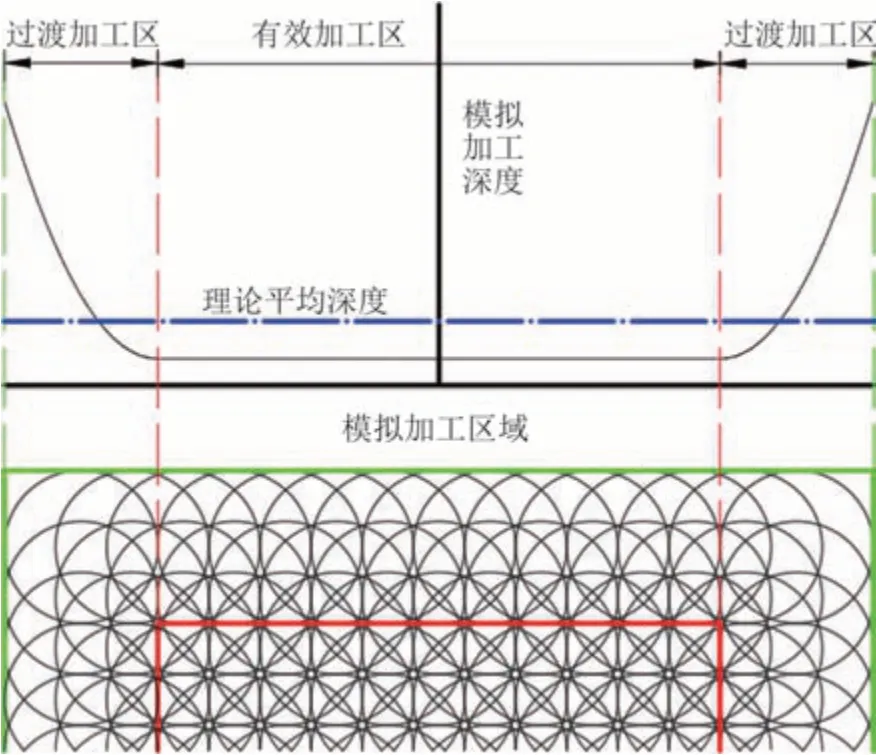
图14 模拟加工区域内部深度-面积区域分布示意图Fig.14 Diagram of depth-area distribution in simulated machining area

另一方面，激光加工的创面形状与激光器的脉冲时间有关，单脉冲加工时间越长，创面周围的熔融物扩散就越明显.图14 所示模拟加工区域与文献［18］加工实验结果趋于一致，由于熔融物扩散现象的存在，加工深度差异减小，而数值模拟未考虑熔融物扩散现象，使得数值模拟和实验加工存在差异.

综上而言，虽然存在一定误差，但数值方法整体可以较好地反应实际激光加工情况，对于干气密封激光开槽相关参数的优化研究，可通过这一方法进行系统分析.

4 参数优化

本文采用TOPSIS（Technique for Order Preference by Similarity to Ideal Solution，逼近理想解排序方法）这一综合评价方法评估光斑直径和填充间距对加工质量的影响，并将加工效率作为评估过程中的可选项.TOPSIS 是多目标决策分析中一种常用的有效方法，又称为优劣解距离法.该方法根据有限个评价对象与理想化目标的接近程度进行排序，要求各效用函数具有单调递增（或递减）性即可，是在对现有的对象中进行相对优劣的评价.

依据实际加工测试数据（槽深、粗糙度各120组），建立深度和粗糙度数据结果矩阵，加工效率采用完成加工所需光斑数量n代替，n值越大表示加工效率越低.定义加工深度ha2为效益型指标（单调递增），加工面粗糙度Ras2和光斑数量n为成本型指标（单调递减）.进而根据是否考虑加工效率建立两种决策模型，一种是综合考虑加工深度、面粗糙度和加工效率（三元素），三者分别占决策得分权重的20%、40%、40%；另一种是不考虑加工效率，仅考虑加工深度和粗糙度（双元素）的影响，二者分别占决策得分权重30%、70%.决策模型如下式所示：

式中：Zi为决策模型的指标权重矩阵（i=1，2）；A1为三元素矩阵；A2为双元素矩阵.

Si在0～1之间，得分越大，代表该方案越好.最终得到两种方案的决策得分分布如图15所示.

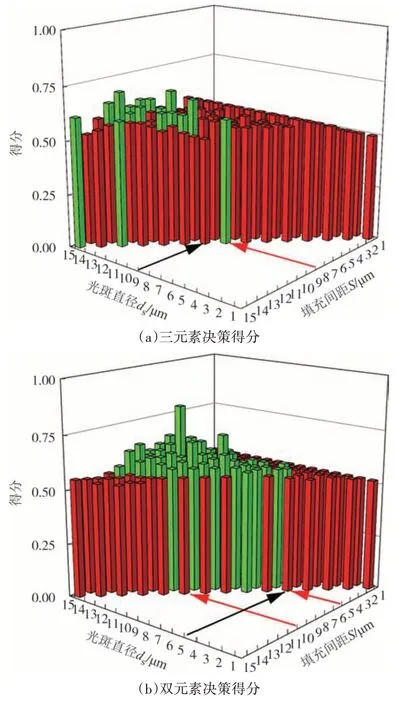
图15 不同决策模型得分Fig.15 Scores of different decision models

由图15 可知，考虑加工效率（三元素模型）时的最优参数区间为8 μm≤S≤15 μm，9 μm≤ds≤15 μm；不考虑加工效率（双元素模型）时的最优参数区间为5 μm≤S≤10 μm，5 μm≤ds≤15 μm.可以看出，对于加工效率的考虑，可以促使最优填充间距范围增大，与实际加工情形相符.

5 结论

1）建立了包含光斑直径和填充间距两个变量的加工深度和粗糙度预测模型，可成功用于指导干气密封精密激光加工.

2）实验表明，连续加工条件下，随着填充间距的增大，加工深度和粗糙度均呈显著降低趋势；调节光斑直径不能显著改变加工深度和粗糙度的大小.

3）对比模拟数据和实验数据的匹配情况，研究了加工深度、粗糙度与光斑直径、填充间距的关系，误差原因主要在于数值模拟未能考虑熔融物扩散和激光加工失焦等因素.

4）采用TOPSIS 综合评价方法，分别得到了是否考虑加工效率情况的最优参数选择区间，结果与实际符合良好.