计及多模态分量的新能源电力系统节点频率分析方法

陈可欣，辛焕海，高晖胜，胡 光，倪秋龙，曹建伟

（1.浙江大学 电气工程学院，浙江 杭州 310027；2.国网浙江省电力有限公司，浙江 杭州 310007；3.国网浙江省电力有限公司 湖州供电公司，浙江 湖州 313000）

0 引言

为实现“双碳”目标，近年来电力系统中新能源占比不断提高。由于新能源出力具有波动大、支撑弱等特性，电力系统频率稳定面临严峻的挑战［1-2］。例如，2016 年9 月28 日，极端天气诱发南澳电网新能源大规模脱网，系统频率快速跌落至47 Hz，从而引发全网崩溃［3］。又如，2019 年8 月9 日，雷击引起英国电网中大量新能源脱网，系统频率跌落至48.8 Hz，引发大规模停电［4］。因此，亟需对新能源电力系统的频率稳定性能进行更深入的研究。

传统频率稳定研究通常仅关注系统全局频率，其反映系统整体的频率支撑能力和受扰情况［5］。例如，经典的平均系统频率模型、系统频率响应模型及众多衍生模型［6］均针对全局频率进行分析。随着电力系统中新能源机组增多，调频资源分布更加不均匀，频率响应的空间分布特性也更加显著［8］。此时，即使系统整体频率支撑能力较强，某些调频资源匮乏的节点仍可能因近区的扰动而产生较大的频率波动，并引发安全稳定事故。因此，近年来频率响应的空间分布差异也受到越来越多的关注［8］。

目前，分析频率空间分布差异的方法大致包含基于仿真测量、基于模型解析2 类。第一类中，文献［8］等针对软件仿真测得的频率轨迹进行分析，建立了节点惯量等多种表征频率空间分布特性的指标。其优势在于结果相对精确，但所得结论缺乏机理解释。此外，分析结果只适用于特定工况及扰动，若要验证所有工况的稳定性则有较大的计算负担［10］。与仿真测量相比，基于解析模型的方法理论性较强，可通过灵敏度分析等进一步指导控制改进。此类方法需要对电网和发电设备分别建模，从而获得系统闭环频率响应。对于电网侧，现有文献大多采用与直流潮流类似的模型［11］。对于设备侧，由于大规模电力系统设备数量众多，采用详细模型将导致频率响应难以解析，故现有方法通常会做出较强假设以简化分析［12］。也有部分文献考虑较详细的设备动态，通过建立分区系统频率响应模型进行分析［14］。但通常对分区数有所限制，无法更精细地分析频率的空间分布情况。值得指出的是，上述2 类方法中，均有文献采用节点惯量指标量化频率空间分布差异。事实上，多机电力系统频率响应中多分量共存［12］，节点惯量只衡量了总频率变化率，无法对不同分量进行单独分析。例如，对于一台虚拟同步机，无论直接给负荷供电或连接无穷大电网，其机端节点惯量均为该设备的惯量，但其频率响应却存在本质差异。前者中，发电设备与负荷的频率接近一致，均为系统全局频率；而后者中，发电设备的频率响应为它与电网之间的相对振荡。现有节点惯量等方法无法对此进行区分，难以更全面、精细地对电力系统的频率响应进行分析并设计控制。因此，分析频率响应的空间分布差异时，有必要区分不同分量进行研究。对此，文献［16］提出了频率模态解耦的分析方法，将系统频率响应分解为共模频率与若干差模频率，分别表征了频率响应中的全局分量与空间分布差异。文献［17］基于发电设备同构／均匀阻尼等假设，解析了各节点在扰动下各模态频率分量的表达式，并分模态定义了有效惯量、模态惯量等指标。然而，新能源调频参数可灵活变化，同步机的参数则较为固定，因此它们的调频行为通常具有异构特性，依赖于同构／均匀阻尼假设的方法难以准确分析新能源电力系统的频率响应。

为此，在文献［16］的基础上，本文进一步提出适用于新能源电力系统的节点频率响应模态分解与量化分析方法。首先，建立了电力系统节点频率响应模型，并将各类型发电设备近似为统一结构以简化分析。然后，利用基于二次特征值问题（quadratic eigenvalue problem，QEP）的方法将频率响应进行分解，近似解析了共模频率、差模频率等模态频率分量。进一步地，解析了各频率分量的变化率、最大偏差量等响应特性，并通过节点模态惯量指标量化分析了不同频率分量在电力系统中的空间分布特性。最后，仿真验证了所提方法的有效性。

1 节点频率响应建模及模态频率分解

首先对新能源电力系统设备侧和网络侧分别进行建模，进而获得系统闭环频率响应模型。然后对现有文献中频率分解方法的局限性进行简要说明。

1.1 电力系统节点频率响应模型

首先，建立网络侧调频动态模型。网络中各节点的相角-有功响应如式（1）所示［11］。由于系统中各节点的频率响应均存在一定差异，故分析时不仅考虑了设备，也保留了网络中无源节点。设备节点和网络节点的编号分别为1 —n和n+ 1 —m。

式中：ΔPGen和ΔPNet分别为发电设备和网络节点的功率变化量；ΔθGen和ΔθNet分别为发电设备和网络节点的相角响应，对其微分即可获得对应节点的频率响应ΔωGen和ΔωNet；L11、L12、L21、L22为设备节点与网络节点的分块拉普拉斯矩阵，由系统的相角-有功潮流方程线性化得到，与系统中设备出力和负荷分布有关，具体表达式见附录A式（A1）。

其次，建立设备侧调频动态模型。一般地，新能源、同步机等发电设备的调频动态可表示为［16］：

式中：G(s)为对角矩阵，对角元为设备的频率-有功传递函数。记第i台设备单位容量的传递函数为gi(s)，标幺容量为fi（即额定容量与容量基准值之比），则其频率-有功传递函数Gi(s)=figi(s)。新能源参与调频时，为简化分析，认为其调频余量充足。

网络节点不会对频率扰动做出功率响应，故有：

值得一提的是，当新能源不参与调频时，对应的设备节点可转变为网络节点进行分析。由式（1）—（3），可得系统的闭环频率响应模型如下：

式中：ω0为系统标称频率；ΔPD，Gen和ΔPD，Net分别为设备节点和网络节点扰动。

为便于理解，接下来简要介绍网络节点与设备节点的相角响应以及功率扰动之间的关系。由式（4）第2行可知，网络节点的相角响应为：

ΔθNet由两部分组成。第一部分为所有设备节点响应的加权，权重系数矩阵为-。该矩阵行和为1 且所有元素非负［19］，该结果与分频器理论分析所得结论基本一致［11］。第二部分则由扰动直接确定。当ΔPD，Net为阶跃扰动时，这一部分的相角响应也为阶跃形式，该响应是潮流平衡的需要。对应的频率响应为脉冲，时间尺度很小，在分析频率响应时通常可忽略。因此，后文将重点关注网络节点响应中的第一部分，记为Δθ′Net。

接下来说明网络节点扰动与设备节点间的关系，将式（5）代入式（4）得：

式中：Ls=L11-L1221； ΔPEq=-L12ΔPD，Net+ΔPD，Gen，为等效扰动，这表明施加在网络节点部分的功率扰动可通过矩阵-L12等效为各设备节点的功率扰动。

由式（6）可知，网络节点的频率响应由设备节点响应加权获得，故后文只需分解式（7）中的设备节点响应，代入式（6）即可获得网络节点的响应。值得一提的是，实际电力系统中发电设备节点、网络节点数以万计，调频资源众多。对上万个节点进行详细分析将过于繁琐，而且没有必要。事实上，可以根据设备间电气距离大小将系统分为若干区域，并通过参数等效聚合／辨识的方法分别等效为单台设备［20］。这本质上是认为区域内频率响应一致，进而研究区域间频率的分布情况。

1.2 现有模态频率分解方法及其局限性

大量工程经验及理论研究表明，电力系统节点频率响应中存在全局一致分量、相对振荡分量等多个分量［12］。系统模态频率示意图如图1 所示，二者表现出的响应特性并不相同，其分析与控制设计方法也存在一定差异。对于各节点频率中全局一致分量，通常期望其最大偏移量不要过大，以免触发低频减载等保护动作；而对于振荡分量，则期望它在波动较小的同时能快速衰减［1］。现有的节点频率分析方法大多未对不同分量进行区分，难以深入研究各节点频率响应的动态过程。

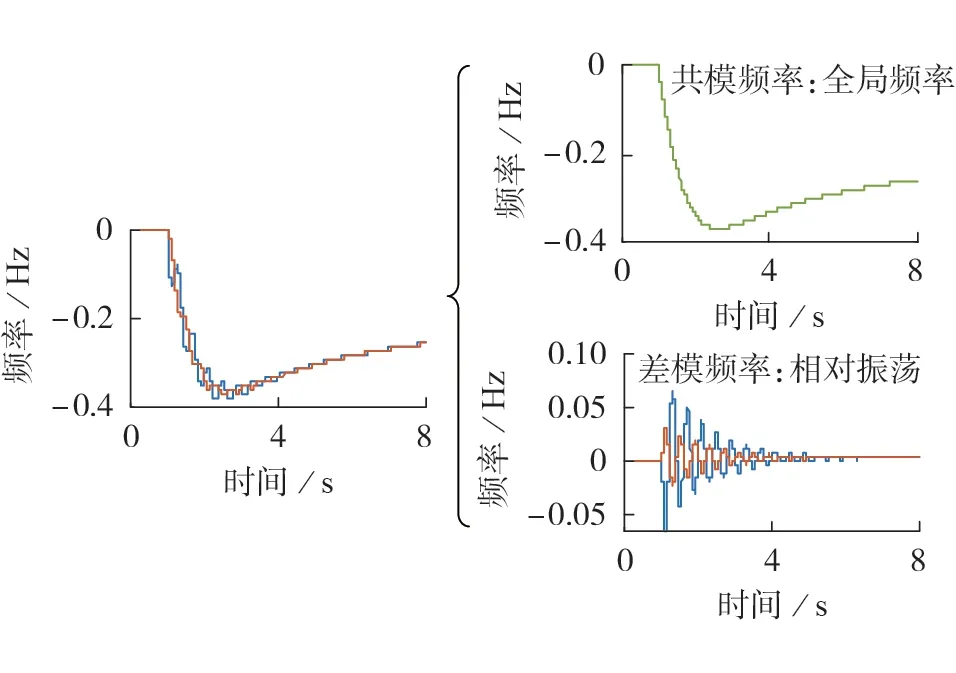
图1 系统模态频率示意图Fig.1 Schematic diagram of system modal frequency

为此，文献［16］提出了模态频率分解方法，基于系统回差矩阵的谱分解将相角（频率）响应分解为多个分量：

式中：Δω1(s)为共模频率，在所有节点其值一致；Δωk(s)（k=2，3，…，n）为差模频率，在节点间其值相对振荡；w/n、I分别为Ls的左、右特征向量；wi为w的元素；λR，k(s)和uR，k(s)、vR，k(s)（k=2，3，…，n）分别为系统回差矩阵的特征值和左、右特征向量。

系统同构时，各设备单位容量传递函数gi(s)相同（记为g(s)），频率分解结果可进一步简化为［17］：

式中：F=diag{fi}为各设备标幺容量组成的系数矩阵；λFL，k为矩阵F-1Ls的第k个特征值。为便于描述，后文将Δωk(s)（k≠1）按振荡频率由小到大分别称为第1差模、第2差模、…、第n-1差模。

不难验证，式（9）中的共模频率和差模频率可分别由图2（a）、（b）所示的单机带负荷系统和单机无穷大系统获得。图中：Geq(s)为等效设备的调频动态；Beq为等效线路电纳。

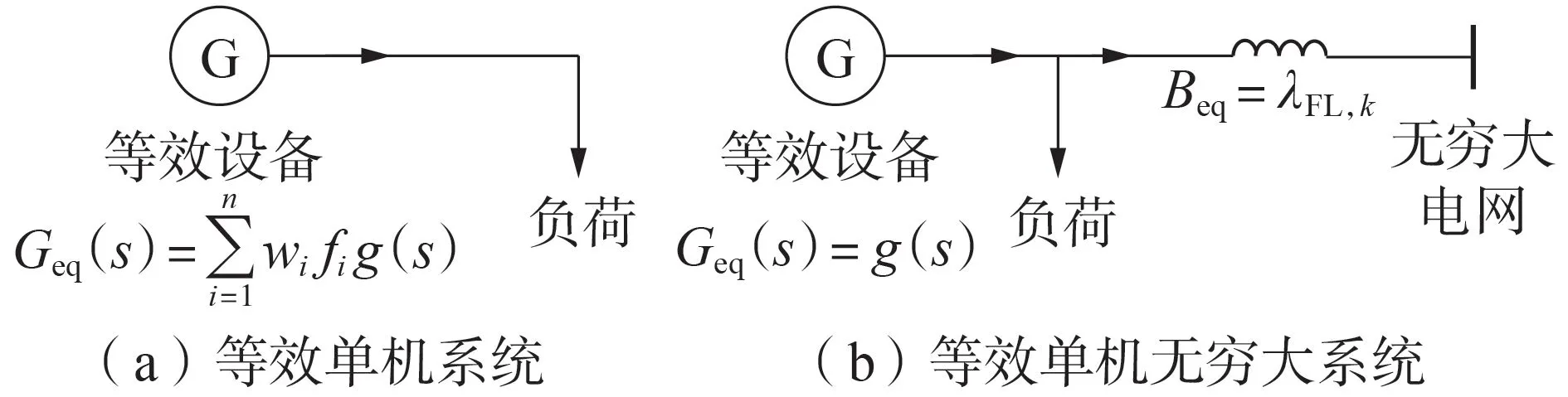
图2 等效系统示意图Fig.2 Schematic diagram of equivalent systems

获得式（9）需依赖于同构的假设。然而，在新能源电力系统中，同步机、新能源等不同设备调频环节差异较大，此时差模频率的轨迹一般难以解析。为此，第2 章将给出一种设备简化建模方法，第3 章在此基础上将频率响应进行分解。

2 适用于模态频率分析的设备简化建模

下面首先介绍适用于模态频率分析的设备简化模型，然后给出简化模型参数的求解方法。

2.1 设备简化模型结构

对于共模频率，由于扰动后一段时间其轨迹通常近似为阻尼正弦曲线（呈现先跌落（上升）后恢复的形式），对应的设备模型为惯量-阻尼-调频系数统一结构，如式（10）所示，故可采用此类结构近似各设备［22］。差模频率为振荡形式，也可由阻尼正弦曲线近似，如附录A 图A1 所示。进而也可采用式（10）所示传递函数Gu(s)近似各设备模型。

式中：Ju、Du、1/Ku为统一结构参数，分别称为统一结构惯量、统一结构阻尼和统一结构调频系数。

统一结构模型较为简洁，一套参数可以表征设备对于某个频率分量的响应特性，但可能并不适用于所有分量。因此，将设备近似为统一结构时应当区分不同模态分量。即对于不同模态，最适合描述设备的统一结构参数并不完全一致，该性质可称为统一结构参数的“模态性”［22］。当然，采用更复杂的模型结构、设置更多参数时，理论上参数的适应性可能更强。但采用惯量、阻尼这种简单的结构进行分析，有助于理解问题并指导工程实践。此外，在分析差模振荡时，本文所提统一结构和经典的阻尼转矩分析具有一定的相似性。而采用阻尼转矩分析得到的一个基本结论就是对于不同振荡频率点，设备阻尼转矩不完全相同，甚至出现较大差异。从中可以看出，参数的模态性可能是难以避免的。另外，需要说明的是，将设备高阶模型简化为惯量、阻尼等形式的低阶模型时，忽略了一些高频动态，特别是电磁暂态尺度的动态。这一过程中，系统会丢失部分特征根，但由文献［16］、图A1及后文算例可知，采用二阶模型可以较好地描述本文关注的惯量、阻尼等主导的机电暂态尺度下的系统频率响应和振荡分量。

将同步机、新能源等设备简化为统一结构后，其调频动态的差异可描述为统一结构参数的差异。不同类型设备统一结构惯量、阻尼等参数比例通常不同，系统仍呈现异构特征（非均匀阻尼）。

基于上述的统一结构模型，对于含n台发电设备的电力系统，各设备节点的频率响应模型（式（6））可降阶为n自由度的二阶模型，具体如下：式中：J′、D′、L′为参数矩阵，且J′=ωJu，D′=ωDu，L′=Ls+ωK，Ju、Du、K为对角阵，其元素为各设备的统一结构参数。

对于式（11）所示相角（频率）响应模型，即使系统中设备异构，通过采用QEP 的方法也可将频率响应分解，并获得各模态频率解析表达式。具体分解方法将在第3章给出。

2.2 统一结构参数求解方法

以第k个频率分量为例，参照文献［22］中方法，可建立如下优化问题求解统一结构参数：

式中：t0为扰动初始时刻；对于共模分量，tf一般取1.5 倍最低点时刻，对于差模分量，统一结构可近似的时间范围更长，tf可取2～3 倍振荡周期；ΔPi，k(t)和ΔP′i，k(t)分别为t时刻第i台发电设备对第k个模态频率的实际功率响应和统一结构近似的功率响应；Jui，k、Dui，k和1/Kui，k为待求解的第i台发电设备第k个模态的统一结构参数；Δωi，k(s)为系统第i个设备节点频率响应的第k个分量，可通过迭代法进行求解。Δωi，k(s)求解流程如附录A 图A2 所示，具体步骤如下：①估计所有发电设备的统一结构参数初值；②根据下文式（15）获得第i个设备节点第k个频率分量近似的表达式Δω′i，k(s)；③将Δω′i，k(s)代入式（12）所示的优化问题进行求解，并更新各设备的统一结构参数；④重复步骤②和步骤③，直至参数收敛。

特别说明的是，对于调频动态更复杂的新能源机组／同步机，采用上述方法对其调频动态进行统一结构近似后，即可进行进一步分析。

3 基于QEP 的频率响应分解及节点模态惯量指标

下面基于QEP 的分解方法将式（11）中频率响应进行分解［5］，并通过建立节点模态惯量指标等方法来分析差模频率的空间分布特性。

3.1 基于QEP的频率响应分解方法

对于式（11）所示的n自由度二阶系统，满足式（13）的λk、zk(k=1，2，…，2n)为其QEP 和相应的右特征向量［5］。

由线性系统理论可知，式（11）所示系统存在2n个特征值。将这2n个特征值的响应两两结合，可以形成n个二阶模式［25］。为获得这些二阶模式具体的表达式，定义以2 组特征值为对角元的对角矩阵，即Λ1=diag{λ1，λ1，…，λn}，Λ2=diag{λn+1，λn+2，…，λ2n}，同时记Ddcp=-Λ1-Λ2、Ldcp=Λ1Λ2。

基于文献［5］的方法，可以将设备节点响应分解为若干个二阶分量，其表达式为：

式中：dk、lk分别为矩阵Ddcp、Ldcp的对角元；变量HM，k、HN，k的表达式和推导式（14）的具体步骤分别见附录B和文献［5］。

结合式（6）和式（14），考虑仅在第j个节点施加大小为P0的扰动ΔPD，j=-P0/s，则第i个节点的频率响应Δω′i(s)为：

式中：O[i，j]表示矩阵O中第i行第j列的元素。

为描述方便，称解耦的频率响应中第k个分量为QEP 分量k。对式（15）进行拉氏反变换，即可获得其时域结果，见附录B式（B11）。

为便于理解，简要说明基于QEP 的频率响应分解与文献［17］中基于同构假设的模态频率分解间的联系。设备同构时，由式（9）知，将设备近似为统一结构后，每个模态频率分量的分母均对应系统一对特征根。而各QEP 分量也对应一对特征根。由留数定理可知，它们分子的系数也相同，故此时2 种分解方法完全一致。QEP 分量1 即为共模频率，QEP 分量k为第k-1差模频率。弱异构系统可视作由一个同构系统摄动而来，此时2 种分解方法相近，因此后文用QEP分量近似表征各模态频率分量以进行分析。

3.2 节点频率响应特性分析

对式（15）中第k个频率分量Δω′i，k(s)应用拉式变换微分定理，可知其变化率Δω˙′i，k(s)的频域表达式为：

式（16）中存在一个常数项-P0H′M，k[i，j]/ω0，该项在系统同构时等于0（证明可参考文献［5］）。在异构时，该项不为0，频率变化率将在扰动初始时刻有脉冲项。这是因为异构系统中各频率二阶分量的初相角不为0°，扰动初始时刻频率分量发生突变。值得注意的是，此处各频率分量的突变与式（5）的网络节点相角突变所指的并非同一个现象，异构系统的设备节点、网络节点均可能发生频率分量的突变。若直接应用初值定理计算其初始变化率，则将得到一个由突变导致的趋于无穷的值。为计算各分量的初始变化率，应用初值定理时可舍去这部分，即：

由此，可以定义节点模态惯量指标Ji，j，k为：

Ji，j，k物理意义为在第j个节点发生单位阶跃扰动时，第i个节点频率响应中第k个分量初始变化率的倒数，当i=j时，可简记为Ji，k。

此外，考虑节点频率响应为各分量的叠加，还可定义节点总模态惯量Jm，i，j如下：

式（19）适用于设备、网络节点，其物理意义为系统中各设备惯量对扰动点的支撑情况。一般而言，节点惯量越大，系统内各设备的惯量资源能为该节点提供更多的惯量支撑作用，在有功扰动下能更好地抑制该节点频率变化，这一节点受到扰动后频率变化得越慢，反之亦然。特别地，在设备节点施加扰动时（i=j），由式（19）计算得到的该节点自身的节点总模态惯量理论上等同于设备的惯量。这是因为各分量的初始变化率之和等同于总的初始变化率，而后者由设备惯量决定［17］。但需要说明的是，式（19）的推导依赖于将设备简化为统一结构，而简化的过程可能会带来误差。故计算得到的节点总模态惯量可能并非严格等于设备惯量，这将在后文算例中进行说明。

与现有的节点惯量相比，通过节点模态惯量指标可区分不同振荡频率的分量中哪些分量振荡／跌落较大，有助于理解不同节点不同模态的频率支撑能力，并在此基础上进行针对性的控制设计，而这是现有的节点惯量指标无法体现的，后文算例对此进行了进一步的说明。

此外，虽然节点模态惯量只与频率分量的初始变化率有严格的解析关系，但是它仍可在一定程度上为分析各频率分量振荡幅值的分布情况提供参考。具体而言，对于同构系统，各节点同一个模态分量的相位相同或相反，此时各频率分量的振荡幅值与其初始变化率成正比，即与节点模态惯量成反比［17］；对于异构系统，由后文算例可知，节点模态惯量在不同节点的数值具有数量级的差异，故各节点振荡幅值差异仍由节点模态惯量的变化主导。在节点模态惯量数值较大（如大于103p.u.）处，频率分量初始变化率趋于0，其轨迹整体的波动也将较小。因此，该指标可以用于初步筛选频率分量振荡幅值较大的区域，对于这些区域可进一步分析最大偏差量等频率特征。

基于式（15），也可直接解析各分量的最大偏差，如附录B 式（B13）（二阶模式阻尼比大于1）与式（B14）（阻尼比不大于1）所示。

4 算例分析

下面通过两机系统算例与十机系统算例，基于MATLAB／Simulink 仿真平台验证所提方法与指标的有效性。为便于理解新能源接入对系统频率响应的影响，同时为简化分析，算例中对新能源机组进行了简化，选择了调频动态较为简单的模型（虚拟惯量加下垂控制），未考虑风电转速变化、光伏最大功率点跟踪等因素的影响。此外，由于关注的问题为机电暂态时间尺度，故采用各设备在平衡点处线性化后的小信号模型，且主要关注各设备的调频环节。同步机采用经典二阶模型，新能源机组忽略了较快的电流内环动态。

新能源机组忽略高频电流内环动态前后的系统频率响应轨迹对比见附录C 图C1。由图可知，二者的区别主要在于初始时刻一快速衰减的振荡分量，在分析时可近似忽略。

4.1 两机系统算例

采用两机系统验证模型简化方法、频率响应分解方法和节点模态惯量指标的有效性，该系统如图3所示。图中：节点1、2 为设备节点；节点3 为两设备间任意位置的网络节点；X1和X2分别为节点1、3 和节点2、3 之间的线路电抗；Ra=X1/（X1+X2），表示网络节点与两设备间的位置关系，Ra=0 表示网络节点与节点1 重合，Ra=1 表示网络节点与节点2 重合；J1、J2分别为设备1、2自身惯量。

图3 两机系统拓扑图及理想情况下模态频率符号解Fig.3 Topology diagram of two-machine system and its symbolic solution of modal frequency in ideal case

为更直观地说明提出的分解方法和指标的具体含义，首先考虑该两机系统为理想系统，即同构，各节点电压为1 p.u.且线路相角差为0°，此时可以得到频率分解结果、模态惯量指标的符号表达式，分别如附录C 式（C1）和图3 所示。网络节点的响应为设备节点的加权和，此处不予展示。

由式（C1）和图3 可知：两设备节点响应中一个分量相同，为共模频率；另一分量符号相反，为差模频率，其幅值沿着线路线性变化。当线路中某点满足X1/X2=J2/J1时，差模幅值为0，差模惯量趋于无穷，当扰动发生在该节点时，系统中不会激发差模振荡。因此，可将该节点视为差模振荡中心。还值得一提的是，容易验证在设备节点处应用式（19）计算节点总模态惯量，分别等同于设备自身惯量J1与J2。

接下来通过如附录C表C1所示的4个算例对统一结构简化建模方法以及频率模态分解方法进行验证。设线路总电抗X1+X2=0.7 p.u.，恒阻抗负载的导纳YLoad=0.8-j0.1 p.u.。算例1 中设备1 以及算例2 中的设备1、2 为同步机（模型见附录C 式（C2）和图C2）；算例1 中的设备2 以及算例3 和算例4 中设备1、2 为虚拟同步机模型（模型见附录C 式（C3））。所有算例中扰动均为在t=1 s时负荷突增。

4.1.1 统一结构近似及模态频率分解有效性验证

首先基于算例1 和算例2 验证统一结构近似方法与频率分解方法的有效性。

在算例1 和算例2 中，分别针对共模频率（QEP分量1）和第1 差模（QEP 分量2），对各设备频率-有功传递函数进行统一结构近似，得到各设备各个模态的统一结构参数，如表1 所示。可以看出，2 个算例中同步机在不同模态下的统一结构参数不同，体现了参数的模态性。算例1中设备2为虚拟同步机，由于采用的简化模型结构与统一结构一致，因此其各模态统一结构参数为其本身的参数。基于统一结构模型，新能源、同步机调频性能的差异可由统一结构参数差异表征。

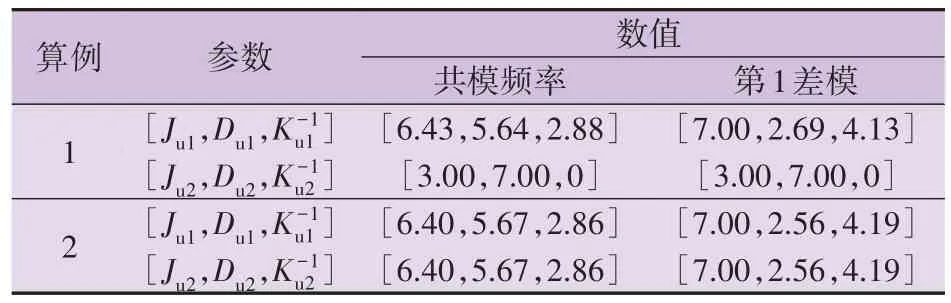
表1 算例1和算例2中设备各模态统一结构参数Table 1 Modal unified structural parameters of equipment in Example 1 and Example 2

进一步，基于式（15）计算各频率分量，叠加获得节点频率响应，如图4（a）、（b）所示。可以看出，所得结果能较好地近似节点频率响应，且结合统一结构近似和所提模态频率分解方法，可较准确地解析系统频率响应。此外，图4（c）、（d）给出了QEP 各分量和模态频率的对比。由图可知，统一结构近似后分解所得QEP 分量1 能较好地表征扰动后一段时间内系统的共模频率，而QEP 分量2 能很好地表征较长时间内系统第1 差模的动态。故后续算例中用QEP分量近似表征各模态频率分量以进行分析。

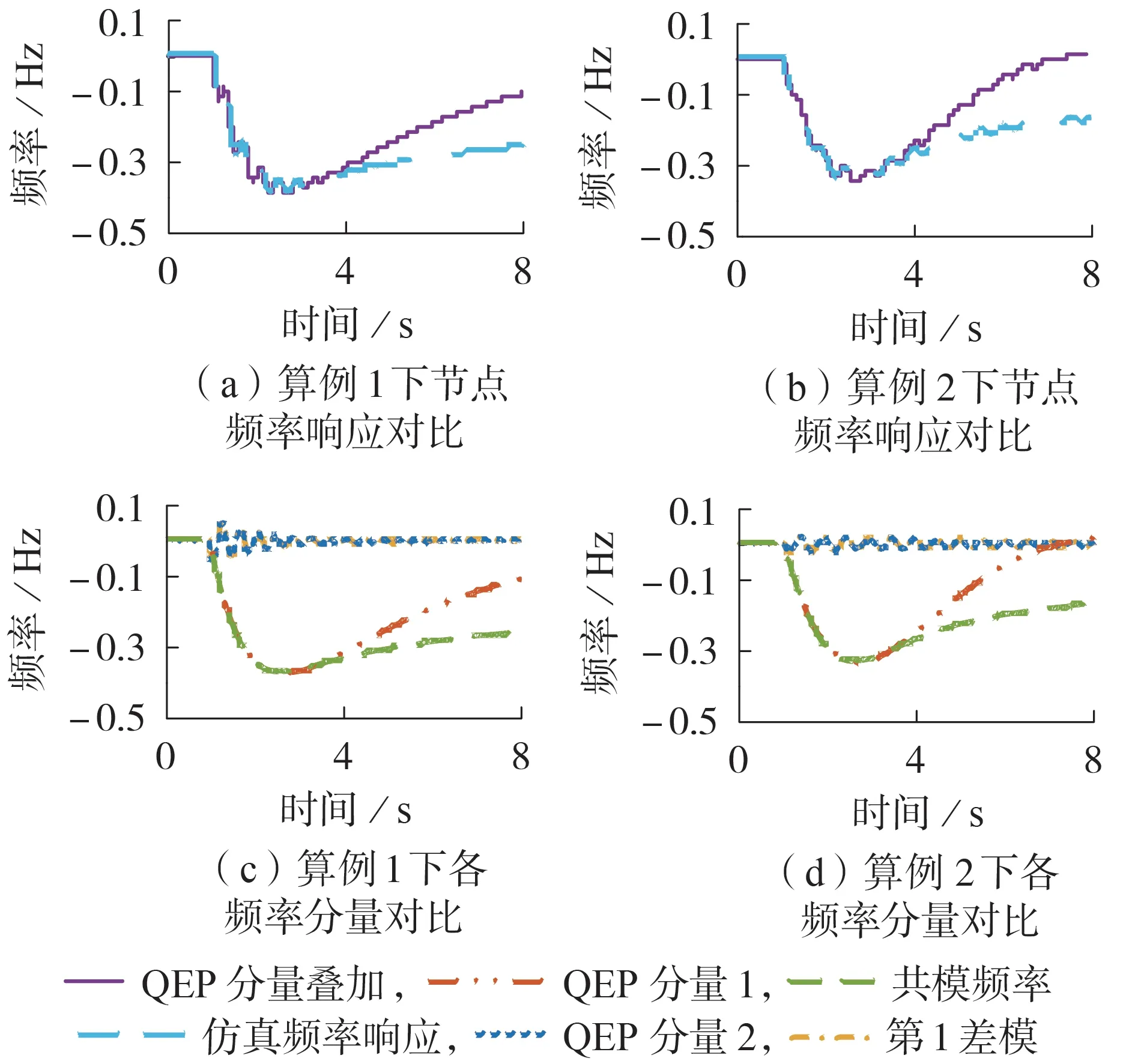
图4 网络节点频率响应仿真以及统一结构近似结果对比Fig.4 Comparison of network node frequency response simulation and unified structure approximation results

4.1.2 节点模态惯量指标验证

下面验证所提节点模态惯量指标的有效性。分别采用本文所提节点模态惯量指标以及现有的节点（总模态）惯量指标衡量两机系统算例3、4 中网络节点的频率特征。2 个算例中网络节点的节点惯量（总模态惯量）均为10 p.u.；算例3 中节点共模惯量为1.0×104p.u.，差模惯量为10 p.u.；算例4 中节点共模惯量为10 p.u.，差模惯量为3.0×103p.u.。这与其在扰动下的频率初始变化率分别对应。

网络节点频率响应及其模态频率分量见图5。

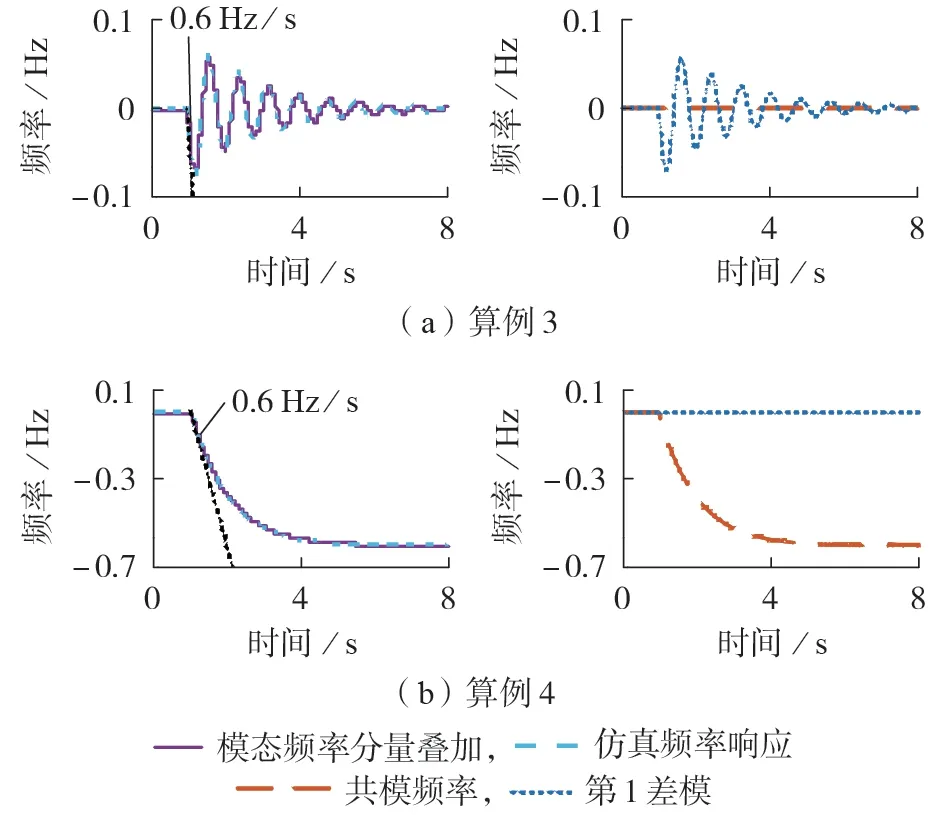
图5 网络节点频率响应及其模态频率分量Fig.5 Network node frequency response and its modal frequency component

节点惯量相同说明2 个算例下网络节点遭受扰动后的频率初始变化率一致，但由图5 可知，二者后续的变化趋势差别很大，现有节点惯量难以体现二者的区别。本文提出的节点模态惯量指标可以对其进行解释：算例3 中共模惯量非常大，说明算例3 下节点频率响应中的共模分量（先跌落（或上升）后恢复的部分）趋于0，频率响应呈现振荡形式；算例4中差模惯量非常大，说明算例4 下节点频率响应中的差模分量（振荡部分）趋于0，频率响应几乎没有振荡，呈现先跌落后恢复的形式。因此，通过节点模态惯量可以较好地区分这2 种情况，而现有的节点惯量仅能得出二者初始频率变化率相同的结论，无法进一步区分不同频率分量的振荡情况，说明了节点模态惯量指标的有效性。

此外，按3.2 节所提方法计算算例1 — 4 下各设备节点的节点总模态惯量，并将其与设备真实惯量值进行对比，如附录C 表C2 所示。可以发现二者误差均在5 % 以内，进一步验证了节点模态惯量指标的有效性。

4.2 十机系统算例

采用10 机39 节点系统，其结构如附录C 图C3所示，验证所提频率响应分解方法在更大规模系统中的适用性，并观察节点模态惯量指标在多机系统中的分布情况。系统中所有设备均为虚拟同步机，下垂系数均设置为20，G1、G7和G10的虚拟惯量为1，其余设备虚拟惯量为8 p.u.。网络拓扑结构与标准IEEE 39节点系统相同。

在节点34施加有功阶跃扰动，附录C表C3给出各节点频率分量最大偏差的理论计算结果与实际值对比，二者相对误差小于5 % ，验证了模态振荡幅值表达式的准确性。附录C 图C4 左侧的子图对比仿真曲线和模态频率响应叠加轨迹。可见二者基本重合，再次验证了所提模态频率分解方法的有效性。

下面分析该系统中频率响应和节点模态惯量指标的分布情况。现有节点惯量指标在系统中的分布情况，如附录C 图C5 所示。可以看出通过节点惯量能够发现系统中的薄弱点，但无法进一步分析不同振荡频率的各分量在系统中的振荡情况。而本文所提节点模态惯量则可以分模态对各个频率分量的空间分布情况进行分析，发现振荡中心以及各机组间的振荡情况，从而有助于更深入地认识频率空间分布差异并进行后续的控制设计。以第1 差模（差模中振荡频率最低的分量）为例，其频率响应振荡幅值的相对大小（以系统中该模式最大幅值进行标幺化）和节点模态惯量指标（标幺值）分别如图6（a）、（b）所示。其中，为更清晰地区分系统中的机组振荡情况，图中将振荡幅值小于0.1 p.u.的区域均用白色区域表示。由图6（a）可知，该算例中第1 差模主要为图中右下角（G4— G7）与其余机组之间的相对振荡。这可从附录C图C4（a）、（b）右侧子图得到印证，也与图6（b）所示节点模态惯量的分布情况对应，即模态惯量越小，振荡幅值越大。特别地，网络节点17 附近模态惯量趋于无穷，其差模频率时域响应趋于0。随着与节点17 距离变远，节点的差模惯量逐渐变小，振荡幅值逐渐增大。由此可知，可将差模惯量数值较大的节点视为该频率分量的振荡中心。

为进一步对比分析不同频率模态分量，附录C图C6还给出了第1、第5和第9差模的振荡幅值以及节点模态惯量分布图，图中模态振荡幅值和节点模态惯量均为标幺值。对于第2 差模，由图C6（b）可知：从左上角G8到右下角G7的区域内，模态惯量值都非常大，可见振荡中心不一定是一个点，也可能是一片区域；并且，振荡中心不一定是传输网络中的节点，也可能包含发电设备。进一步结合图C6（a）可知，该分量主要为G4、G5、G9与G1— G3之间的相对振荡。值得指出的是，G4、G5与G9之间被振荡中心分隔开，这意味着同一个模式同向振荡的机组，也可能分属多个区域。此外，对比图6（b）和图C6（b）、（d）、（f）可知，随着振荡频率上升（从第1 差模到第9 差模），系统振荡中心的范围总体呈扩大趋势，包含的设备数量增多，即参与振荡的机组变少。与图6（a）和图C6（a）、（c）、（e）中各机组的振荡情况相吻合。

表2 总结了以上几个模态下系统中参与振荡的机群及其总惯量（标幺值）。可见，随着振荡频率上升，参与振荡的机组数量及其惯量之和都相应减少。

5 结论

针对含有异构设备的新能源电力系统差模频率难以解析、节点频率性能难以量化的问题，提出了基于QEP 的频率响应分解方法，并建立了节点模态惯量指标，得到主要结论如下。

1）基于设备统一结构简化建模及QEP 分解方法，可近似解析新能源电力系统各节点模态频率。所提方法初步解决了具有多样化调频资源的电力系统节点频率响应难以解析的问题，并为研究惯量、阻尼分布对节点频率响应的作用机理提供了一种思路。

2）所提节点模态惯量指标分不同模态量化了电力系统中各节点的频率抗扰能力，相较于目前只考虑总体频率响应的节点惯量指标，能更精细地表征频率响应的空间分布特性。指标在网络中的分布具有数量级的差异，可用于初步筛选模态频率分量可能存在较大偏差的区域。

3）在指标数值较大（如大于103p.u.）处，该模态的频率振荡幅值接近0，可视为该频率分量的振荡中心。振荡中心不一定是传输网络中的一个点，可能是一片区域，也可能包含设备节点（即通常所说的不参与振荡）。振荡中心将不同的振荡区域分隔开。研究发现，随着振荡频率上升，振荡中心范围扩大，包含的设备数增多，而参与振荡的设备数下降。

考虑更复杂的新能源设备调频动态，分析各设备惯量、阻尼等参数对频率空间分布的影响，并基于此优化设备进行调频控制设计，是未来的工作之一。

附录见本刊网络版（http：//www.epae.cn）。