基于自适应幂级数初始点的电力系统全纯嵌入潮流并行计算

2023-11-11张道远陈厚合

电力自动化设备 2023年10期

姜涛，张道远，李雪，张勇，陈厚合

（东北电力大学现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林吉林 132012）

0 引言

潮流计算是电力系统规划与运行的基础。目前，牛顿-拉夫逊（Newton-Raphson，NR）法已在电力系统潮流计算中广泛应用［1-2］，但采用NR 法求解潮流存在以下不足［3-4］：NR 法对初值敏感，不合理的初值将导致潮流计算收敛速度慢甚至不收敛；高维潮流雅可比矩阵易奇异，从而导致潮流计算结果不收敛。随着高比例可再生能源的并网以及电力电子装备的大规模应用［5］，电力系统运行环境更加复杂多变，这使得采用NR 法求解电力系统潮流时的初值选取愈加困难。此外，在电力供应日益紧张的背景下，当电网运行处于临界状态［6］时，采用NR 法计算潮流会使雅可比矩阵奇异，从而导致潮流求解失败的风险增大［7］。为适应未来电力系统运行场景复杂多变的趋势［8］以及提高电网安全稳定分析效率，亟需探索适用性更好的潮流计算新方法［9］。

全纯嵌入法（holomorphic embedding method，HEM）是一种高维非线性方程组求解方法，不同于NR 法，该方法基于复分析理论，采用递归思想求解非线性方程组，无须设定初值，不形成雅可比矩阵，具有全局收敛性，在求解电力系统潮流时具有诸多优势［10］。文献［11］首次将HEM 引入电力系统潮流计算中，提出基于全纯嵌入的电力系统潮流计算构想，构建PQ 节点的HEM 潮流模型；文献［12］探讨电力系统潮流计算中的PV 节点HEM 建模方法；文献［13］提出电力系统的全纯嵌入潮流计算方法（holomorphic embedding load flow method，HELM），并从算法收敛性的角度论证该方法在系统潮流有解时可准确收敛至系统真实解，在潮流无解时可通过潮流解振荡发出无解信号［14］；文献［15］计及换流站的控制特点，将HELM应用到交直流电力系统的潮流计算中。

然而，HELM 仍存在以下问题［16-17］：①HELM 在求解电力系统潮流时参考平启动方式确定电压幂级数初始点，当系统规模较大，潮流解的实际电压值偏离该初始点时，虽然HELM 能求解出系统潮流解，但其收敛所需的幂级数阶数较高，计算量较大，从而导致计算耗时增加；②在求解各节点电压的过程中，基于Padé 近似的节点电压解析延拓法的计算量较大，计算耗时较长。为解决问题①，文献［18］结合迭代法与HEM，将高斯-赛德尔法或快速解耦法迭代3次的计算结果作为HELM 的电压幂级数初始点，在一定程度上改善了HELM 的收敛性，但计算过程复杂，收敛速度也受高斯-赛德尔法或快速解耦法计算结果的影响。为解决问题②，文献［19］计及高阶Padé近似的Froissart doublets 效应，采用潮流重启计算策略来缩短HELM 求解电力系统潮流过程中Padé近似的计算耗时，在一定程度上提高了Padé 近似的计算效率，但其根本仍是基于中央处理器（central processing unit，CPU）的串行架构进行计算。随着系统节点规模的增大，HELM 中Padé 近似的总计算量将急剧增加。由于系统各节点电压的Padé 近似计算间相互独立，存在并行潜力，因此，文献［20］采用矩阵拼接的方式将各节点电压Padé 近似计算中的线性方程组进行合并，并利用图形处理器（graphics processing unit，GPU）对其进行并行求解，实现了各节点电压Padé 近似的并行计算，但合并后的矩阵维度随着系统节点规模的增大而急剧增大，且矩阵元素也随着幂级数阶数的增加而变化，这导致CPU 与GPU 间的数据交互频繁且交互量增大，从而使数据交互耗时显著增长，降低了GPU并行计算效率。

本文提出一种基于自适应幂级数初始点的全纯嵌入潮流并行计算方法。首先，根据节点导纳矩阵和平衡节点电压自适应调整系统全纯嵌入潮流方程中节点电压幂级数系数的初始点，进而构建基于自适应幂级数初始点的全纯嵌入潮流方程；其次，基于幂级数系数递归关系式建立幂级数系数求解递归方程组，并求解幂级数系数，实现全纯隐函数显式化；然后，根据Padé 近似的计算特点，基于Numba 的多核CPU 并行计算架构实现各节点电压Padé 近似的并行化，以提高潮流计算效率；最后，通过节点数在4～13 802 范围内的不同规模测试系统算例对所提全纯嵌入潮流并行计算方法进行验证和分析。

1 电力系统潮流的全纯嵌入计算方法

不同于NR 法采用数值迭代思想将非线性潮流方程近似转化为线性方程进行求解，HELM 采用递归思想求解电力系统潮流，基于复分析理论构造节点电压和PV节点无功功率的隐式全纯函数，利用全纯函数幂级数的展开特性，通过求解全纯函数的幂级数将隐式全纯函数显式化，实现对潮流方程的求解。HELM 将非线性潮流方程求解问题转化为隐式电压函数的显式化求解问题，因此，无须预设初值，也不形成雅可比矩阵，理论上该方法有良好的收敛性。

采用HELM 求解潮流包括全纯嵌入潮流模型的构建和全纯嵌入潮流模型的求解2个部分。

1.1 电力系统全纯嵌入潮流模型的构建

在直角坐标系下，节点数为N的电力系统潮流方程［21］可表示为：

式中：Yij为连接节点i、j的支路导纳；Vi为节点i的电压相量；S～i为节点i的注入功率；“*”为共轭运算符。

根据电力系统不同类型节点的特点［13］，在式（1）中嵌入复变量α，构造关于α的各节点电压的全纯函数和PV 节点无功功率全纯函数，参考文献［15］，传统电力系统潮流的全纯嵌入方程为：

式中：l、p、w分别为PQ 节点、PV 节点、平衡节点编号；Ylk，tr、Ypk，tr、Yl，sh、Yp，sh分别为串联支路导纳矩阵中第l行第k列元素、串联支路导纳矩阵中第p行第k列元素、PQ 节点l对地并联支路导纳、PV 节点p对地并联支路导纳；Vk(α)、Vl(α)、Vp(α)、Vw(α)分别为节点k、l、p、w电压的全纯函数；Pp为节点p的注入有功功率；Qp(α)为节点p无功功率的全纯函数；Vpm为节点p的电压幅值；Vwm为节点w的电压幅值。

全纯嵌入相关理论如附录A所示。

1.2 电力系统全纯嵌入潮流模型的求解

不同于传统NR 法采用数值迭代思想求解非线性潮流方程，HELM 采用递归思想求解电力系统潮流。HELM 的求解过程可总体分为幂级数初始点的获取、幂级数系数递归求解方程的构建、全纯嵌入潮流函数的显式化、Padé 近似4 个部分，限于篇幅，详细求解过程如附录B 所示。由式（B3）可知，HELM通过求解初始状态得到电压幂级数初始点（电压幂级数常数项）。在任意系统中，由Ylk，tr、Ypk，tr构成的导纳矩阵对称且每行元素之和为0，此外，平衡节点电压幂级数初始点Vw［0］和PV节点电压幂级数初始点Vp［0］均为1+j0 p.u.，因此，当且仅当所有PQ 节点电压幂级数初始点Vl［0］同时为1+j0 p.u.且所有PV 节点的Qp［0］同时为0 时，才可求得HELM 电压幂级数初始点为1+j0 p.u.。可知，传统HELM 电压幂级数初始点只能固定为1+j0 p.u.。然而，当系统规模较大时，网络拓扑更为复杂，实际电压解偏离1+j0 p.u.较多，这将导致传统HELM 需较高的幂级数阶数才能实现潮流收敛。由Padé 近似部分可知，基于斯塔尔理论，对角／近对角Padé近似函数可生成幂级数最大解析延拓［22］，以保证电压全纯函数在α=1 处可靠收敛，本文采用Padé 近似实现各节点电压解Vx（1）（x=l，p，w）的准确求取。

2 基于自适应幂级数初始点的全纯嵌入潮流计算方法的潮流并行求解

针对传统HELM 在求解电力系统潮流时参考平启动模式确定节点电压幂级数的初始点，可能导致潮流收敛所需幂级数阶数增大，从而导致计算耗时增加的问题，本文提出一种基于自适应幂级数初始点的全纯嵌入潮流计算方法（adaptive power series initial point based holomorphic embedding load flow method，A-HELM）。A-HELM 根据节点导纳矩阵和平衡节点电压自适应调整电压幂级数初始点，以提高潮流收敛性和计算效率。同时，考虑到求解较大规模系统全纯嵌入潮流时，在采用基于Padé 近似的解析延拓法求解各节点电压的过程中，各节点电压的Padé 近似计算彼此独立，具有良好的并行潜质特点，借助多核CPU的多线程计算优势，将A-HELM 中逼近各节点电压真实解的Padé 近似计算过程并行化，以提升全纯嵌入潮流的求解效率。

2.1 电力系统的A-HELM潮流计算模型

首先，构建电力系统的A-HELM 潮流计算模型，然后，利用待定系数法推导A-HELM 潮流计算模型的幂级数系数递归求解方程，实现A-HELM 潮流计算模型的求解。

2.1.1 A-HELM潮流计算模型的构建

将式（1）所示潮流方程采用矩阵形式表示为：

式中：Y为节点导纳矩阵；V为节点电压向量；S为节点注入复功率向量。

由于平衡节点的电压幅值和相角已知，参考NR法计算潮流的方法，不计及平衡节点功率方程，则式（3）变为降阶潮流方程，如式（4）所示。

式中：Yreduced、Vreduced、Sreduced分别为不计及平衡节点的节点导纳矩阵、节点电压向量、注入功率向量；Islack为平衡节点的等效注入电流向量，如式（5）所示。

式中：Yslack为由平衡节点与其余节点间互导纳元素组成的列向量；Vslack为系统平衡节点电压。

将Yreduced拆分为串联支路导纳矩阵Yred，tr和对地并联支路导纳矩阵Yred，sh两部分，如式（6）所示。

为便于理解，以包括1个平衡节点、2个PQ 节点和2个PV节点的5节点系统为例，简要描述式（3）—（6）中矩阵的变化过程，如附录C图C1所示。

将式（6）代入式（4）得：

在式（7）中嵌入复变量α，可得：

根据不同类型节点的特点，由式（8）得到PQ 节点和PV节点的A-HELM潮流计算方程为：

式中：Ylw、Ypw分别为PQ节点l与平衡节点w间的互导纳、PV节点p与平衡节点w间的互导纳。

为使A-HELM 嵌入方程可解，应保证线性方程组数量与待求变量数量相等。考虑到PV 节点的电压幅值Vpm已知，电压相角未知，应补充A-HELM 的PV节点电压幅值约束方程，如式（10）所示。

当式（9）和式（10）中复变量α=0 时，将式（3）代入式（9）和式（10），得到A-HELM的初始状态为：

为求解式（11），将式（3）代入式（7），并令α=0，得到：

将式（5）代入式（12），则式（11）中A-HELM 潮流方程的电压幂级数初始点可由式（13）求得。

式中：Vreduced[]0 为所有电压幂级数初始点组成的列向量；Vw为平衡节点w的电压幅值组成的列向量。

由式（11）—（13）可知，A-HELM 的节点电压幂级数初始状态是由系统参数决定的。与式（4）所示的HELM 电压幂级数初始状态对比可知，所提A-HELM 不是将各节点电压幂级数初始点强制设置为1+j0 p.u.，而是根据系统参数获取幂级数初始点。随着系统运行状态的改变，A-HELM 可根据系统节点导纳矩阵生成的Yred，tr、Yslack和平衡节点电压Vslack实现对节点电压幂级数初始点的自适应调整。

相较于传统HELM，所提A-HELM 具有如下特点：在潮流计算方程中无须对平衡节点进行建模；嵌入方程中的节点电压幂级数初始状态根据系统参数特征进行选取，以加快电压幂级数的收敛速度。

为确保所构建的A-HELM 潮流计算方程具有可行性，应检验所构建的A-HELM 全纯嵌入潮流方程是否满足以下4 个条件［2］：①当嵌入的复变量α=0时，系统各节点电压的幂级数初始点真实存在且易于求取；②当α=1 时，对应实际潮流解，此时全纯嵌入潮流方程应与原潮流方程完全等价；③所构造的待求隐式函数具有全纯性；④根据斯塔尔定理，在到达鞍节分岔点前的α路径上，全纯嵌入潮流方程具有唯一解。

对于条件①，由式（13）可得到A-HELM 幂级数初始点，因此，所提方法满足条件①。对于条件②，当α=1 时，式（13）完全等价于式（1）的原潮流方程，因此，所提方法满足条件②。对于条件③和条件④，采用HELM 求解电力系统潮流的合理性和实用性已被验证［23］，A-HELM 仅是对HELM 的嵌入方程进行恒等变换，而未破坏嵌入方程的全纯性和解的唯一性，因此，所提方法满足条件③和条件④。

综上可知，所构建的潮流计算模型合理且可行。

2.1.2 A-HELM潮流计算模型的递归求解

借鉴HELM求解电力系统潮流的基本思路，采用A-HELM求解式（9）、（10）的幂级数系数过程如下。

为便于描述，令Xx(α)=1/V*x(α*)(x=l，p，w)，将式（3）代入式（9）、（10）所示的A-HELM 潮流计算方程，基于同次幂级数系数的待定系数法，分别构建PQ节点的电压幂级数系数递归求解方程以及PV 节点的节点电压和无功功率的幂级数系数递归求解方程，分别如式（14）、（15）所示。

为便于计算，将式（14）、（15）中复数方程的实部和虚部拆分为纯实数型线性方程。由于复数型递归关系式两侧实部、虚部分别相等，可得对应的实数型递归方程为：

式中：Glk、Blk分别为串联支路导纳矩阵中第l行第k列导纳元素的实部和虚部；Gpk、Bpk分别为串联支路导纳矩阵中第p行第k列导纳元素的实部和虚部；“（Re）”“（Im）”分别表示相应复数的实部、虚部，后同。

根据式（16）所示的幂级数系数递归求解方程组，可由电压幂级数初始点Vx[0] (x=l，p，w)逐阶获取各阶幂级数系数Vx[k]和Qx[k]，实现A-HELM 中各节点电压全纯函数Vx(α)和PV 节点无功功率全纯函数Qx(α)的显式化。

2.2 Padé近似并行化

目前，在电力系统潮流并行计算领域，关于交流潮流并行化的研究主要聚焦于加速修正方程组的并行求解。然而，对于全纯嵌入潮流的计算，Padé近似部分的计算耗时在其潮流求解总时间中占比较高，其原因在于，虽然采用近对角Padé 近似法可提高单个节点电压的解析延拓计算效率，但仍需对系统中每个节点的电压逐一进行Padé 近似计算，即串行计算系统各待求节点的电压，具体过程如附录C 图C2所示，随着系统节点规模的增加，A-HELM 中Padé近似的总计算量也将显著增大。由于A-HELM 需对各节点电压依次进行Padé 近似且近似过程相互独立，因此，所提A-HELM 的Padé 近似过程具有较高的潜在并行能力，可根据节点电压Padé 近似的计算特点设计相应的并行计算架构，并采用合适的并行计算技术将各节点电压解析延拓的Padé 近似计算过程并行化，以提升Padé近似的总体计算效率。

针对数值并行计算，Anaconda 公司推出了Python 环境下的Numba 高性能计算库，以解决工程科学计算领域中的数值计算密集型问题。Numba采用即时编译技术，基于Numba 并行架构可对Python原代码进行编译优化，加快运行效率，且可释放Python 中的全局解释器锁，以多线程并行计算的方式实现自动并行化，为此，本文借助Numba 高性能计算库实现所提A-HELM潮流求解的并行化。

所提A-HELM 潮流方程节点电压的Padé 近似过程中涉及大量的数组运算，结合Numba 并行架构的优点，可借助Numba 对A-HELM 中的Padé 近似函数代码进行即时编译，并在此基础上进行并行化处理，以提高Padé近似的效率，进而提升所提A-HELM的潮流求解效率。Numba的CPU自动并行化技术可自动识别具有并行计算潜力的数值计算部分并对其进行优化处理，以生成最优并行方案，再将计算任务分割为若干个独立的子任务，以并行执行计算任务。在所提A-HELM 的节点电压Padé 近似过程中，由于各节点电压的Padé 近似计算互不依赖，不受计算顺序的影响，Numba可识别该特点，进而将各节点电压Padé 近似的串行计算过程拆分为多个独立的子任务，并映射至各CPU 核中进行计算，在不影响计算准确性的基础上实现各节点电压Padé 近似的并行化。基于Numba 并行架构，所提A-HELM 的节点电压Padé近似并行计算实现流程如图1所示。

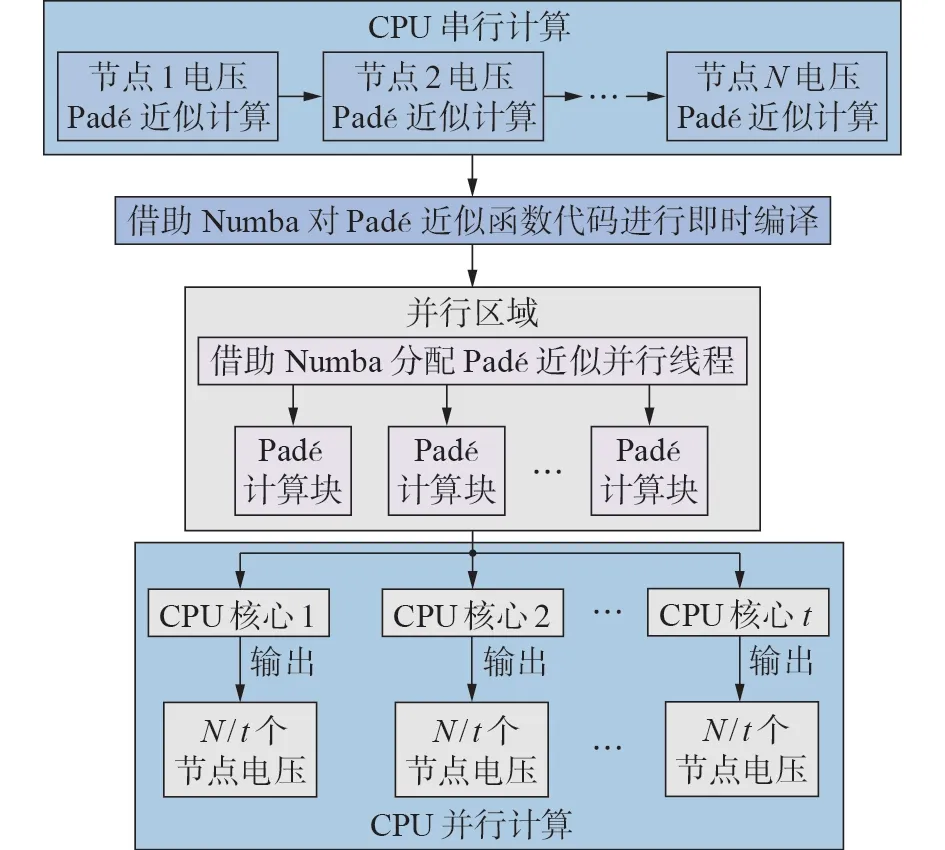
图1 Padé近似并行计算示意图Fig.1 Schematic diagram of parallel calculation of Padé approximation

图1 中，在对Padé 近似函数代码进行即时编译的基础上，Numba开辟并行区域，以划分计算块的方式将各节点电压Padé 近似的计算任务分解为若干个独立的子任务，并为并行区域的各线程分配1 个Padé 计算块。考虑到每个节点电压Padé 近似的计算量基本相同，为使各并行线程的计算负载均衡，可采用类似于OpenMP 中的线程静态调度方式来划分Padé计算块［4］，即各Padé计算块大小（子任务包含的节点数）相等，从而均匀分配计算任务。以包含N个待求节点的系统为例，Numba 自动根据CPU 的核数安排t个线程进入并行区域的迭代块，每个Padé 计算块的大小为N/t，即每个线程负责执行N/t个节点电压的Padé 近似计算，因此，在不同的CPU 核中将同时执行并行区域的t个线程，进而将A-HELM 中逐次求解各节点电压的Padé 近似计算任务均衡分配至各处理器核中，实现多核CPU 平台下节点电压Padé近似的并行化。

2.3 计算流程

综上，所提基于A-HELM 的并行计算方法流程如附录C图C3所示，具体步骤如下。

1）根据式（13），由系统节点导纳矩阵与平衡节点电压计算系统潮流的幂级数初始点。

2）利用式（16）所示的递归关系，由幂级数初始点开始逐阶计算各阶电压幂级数系数。

3）对所求得的电压幂级数系数进行近似计算，采用式（B14）所示的Padé 近似方法计算各节点电压近似值，并将此计算过程交由多核CPU进行并行处理。

4）由式（17）和式（18）计算得到各节点功率组成的列向量Scalc及其最大功率不平衡量max_mis。

式中：VPade为所有节点电压近似值组成的列向量；“·”表示向量点乘运算；Scalc_PQ为由VPade计算得到的PQ 节点的复功率列向量；SPQ为系统已知的PQ 节点注入的复功率列向量；Pcalc_PV为由VPade计算得到的PV 节点的有功功率列向量；PPV为系统给定PV 节点注入的有功功率列向量；mPQ为PQ 节点复功率不平衡量列向量；mPV为PV 节点有功功率不平衡量列向量；mPQ(a)、mPV(b)分别为mPQ、mPV的第a、b个元素。

5）将max_mis与给定潮流收敛精度ε进行比较：若max_mis＜ε，则输出系统潮流解；否则返回执行步骤2）— 4），直至幂级数阶数达到阶数上限，若此时max_mis仍不小于ε，则程序终止，输出“算法不收敛”。

3 算例分析

为验证所提基于A-HELM 的并行计算方法的准确性和可行性，通过不同规模的测试系统对该方法进行分析和验证，测试系统相关信息如附录C 表C1 所示。计算平台硬件配置为CPU AMD Ryzen5 4 600 H，6核12线程，主频为3.00 GHz，内存为16 GB；软件平台采用Anaconda 的Spyder 平台（Python 版本为3.8.8）。基于该软件平台开发所提A-HELM 并行计算方法，并将其潮流计算结果与基于NR 法的开源潮流计算软件PYPOWER 的计算结果进行对比［24］。算例中潮流收敛精度均为10-3p.u.。

3.1 方法准确性与通用性验证

3.1.1 方法准确性验证

本节以Case 6ww 测试系统为例，详细说明采用所提方法求解电力系统潮流的基本过程。

首先，根据本文基于自适应幂级数初始点的全纯嵌入潮流计算流程，生成Case 6ww 测试系统的节点导纳矩阵Y，并从Y中提取Yslack和Yreduced，进一步根据式（6）求取Yred，tr，矩阵变化过程如图C3所示。

然后，将Case 6ww 测试系统的Yred，tr、Yslack、Vslack代入式（13），求取节点电压幂级数初始点。根据式（16）的幂级数系数求解递归方程，利用所提方法得到的幂级数初始点V1［0］—V5［0］求取各待求节点电压的1阶幂级数系数V1［1］—V5［1］，此时，式（B14）所示电压幂级数表达式为Vx（α）=Vx［0］+Vx［1］α，对应的潮流最大功率不平衡量为0.104 3 p.u.，大于潮流收敛精度10-3p.u.，不满足潮流收敛条件，因此，需返回式（16），由幂级数系数递推关系式继续求取各节点电压的2 阶幂级数系数V1［2］—V5［2］，再通过Padé近似计算获得新的电压解，并判定是否满足潮流收敛条件，如此循环，直至满足潮流收敛判定条件。电压幂级数初始点以及1 阶和2 阶幂级数系数如附录C表C2所示。图2展示了潮流求解过程中电压幂级数阶数与最大功率不平衡量的关系（图中ΔPmax为系统最大功率不平衡量，为标幺值，后同）。

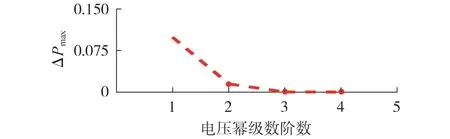
图2 电压幂级数阶数与最大功率不衡量的关系Fig.2 Relation between voltage power series order and maximum power unbalance

由图2 可知，随着电压幂级数阶数的增加，系统最大功率不平衡量减小，即潮流收敛精度与幂级数阶数密切相关，幂级数阶数越高，潮流计算精度越高，但计算耗时也随之增加。Case 6ww 测试系统仅需3 阶电压幂级数即可实现潮流快速收敛，利用AHELM 得到的各节点电压3 阶幂级数系数和各节点实际电压解如表C2所示。

表1为Case 6ww测试系统中A-HELM 串行计算方法与NR 法潮流计算结果的对比（表中2种方法的电压幅值为标幺值，相对误差为A-HELM 串行计算方法结果相对NR 法结果的误差，后同）。由表可知，A-HELM 串行计算方法与NR 法的潮流计算结果几乎一致，最大相对误差小于0.2%，由此验证了所提A-HELM 串行计算方法可实现电力系统潮流的准确求解。

表1 Case 6ww测试系统中A-HELM串行计算方法与NR法潮流计算结果的对比Table 1 Load flow calculation results comparison between A-HELM serial calculation method and NR method in Case 6ww test system

Case 6ww 测试系统中A-HELM 并行计算方法与NR 法潮流计算结果的对比如附录C 表C3 所示。由表可知，相较于NR 法，A-HELM 并行计算方法的最大相对误差也小于0.2%，验证了所提A-HELM 并行计算方法可实现潮流的准确求解。

A-HELM 串行计算方法、A-HELM 并行计算方法、传统HELM、NR 法求解Case 6ww 系统潮流所需时间的对比如附录C 表C4 所示。由表可知：相较于传统HELM 和NR 法，所提A-HELM 计算方法的计算效率有所提高；相较于所提A-HELM 串行计算方法，所提A-HELM并行计算方法的计算效率进一步提高，但由于Case 6ww 测试系统的节点数较少，潮流求解的总计算量相对较小，因此，对Padé 近似的并行化并未使计算效率显著提升，但随着系统规模的扩大，所提A-HELM并行计算方法的优势将进一步凸显。

3.1.2 方法通用性验证

本节进一步通过节点数为4～13 802的不同规模测试系统对所提A-HELM 串行和并行计算方法进行测试，计算过程与Case 6ww 测试系统的潮流求解过程大体一致。以NR 法的计算结果为基准，不同规模测试系统中A-HELM 串行计算方法与A-HELM 并行计算方法潮流计算结果的最大误差如附录C 表C5 所示。由表可知，所提A-HELM 串行和并行计算方法的节点电压幅值及相角最大相对误差均小于0.1 %，有效验证了所提方法可实现不同规模电力系统潮流的准确计算，具有良好的通用性。

3.2 方法收敛性验证

为验证所提方法的收敛性，本节对比所提AHELM串行计算方法、传统HELM、NR法在不同规模测试系统下的计算耗时，结果如表2所示。

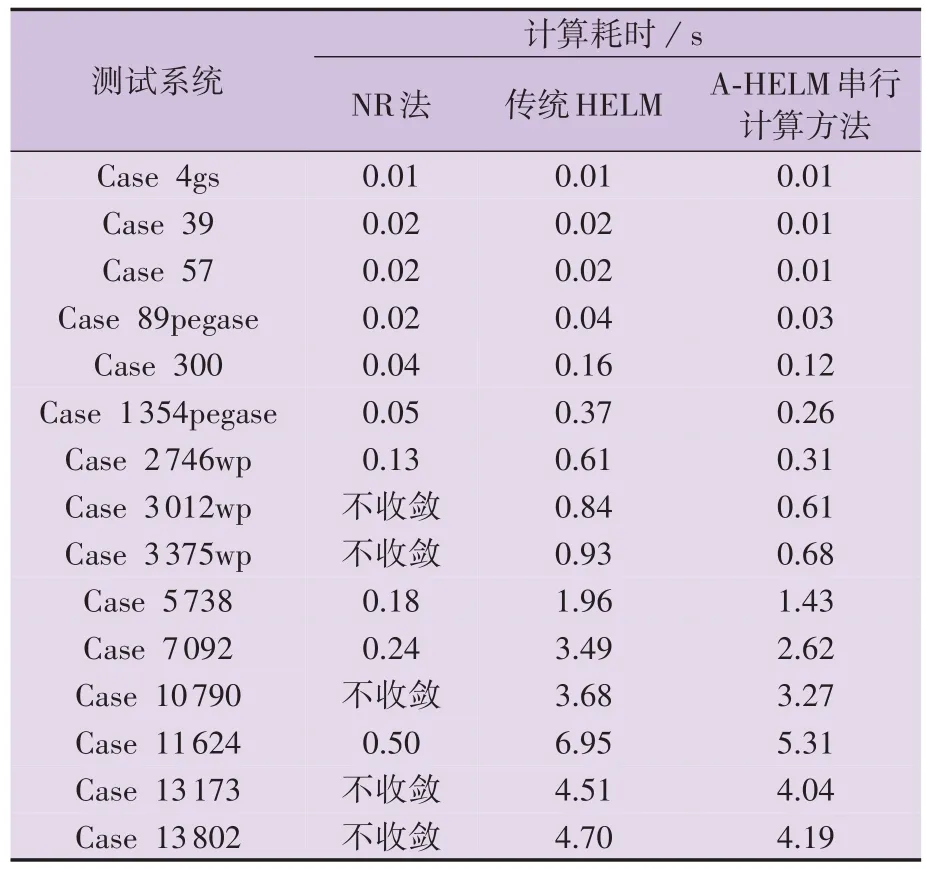
表2 A-HELM串行计算方法、传统HELM、NR法的计算耗时对比Table 2 Calculation time comparison among A-HELM serial calculation method，traditional HELM and NR method

由表2 可知，随着测试系统规模的扩大，系统网络拓扑更加复杂，NR 法不收敛的问题愈加严重，这主要是由于NR 法采用平启动初值，无法满足潮流收敛条件，而对于NR 法不收敛的测试系统，所提AHELM串行计算方法均可收敛至系统潮流解。

A-HELM 串行计算方法与传统HELM 幂级数初始点潮流计算耗时的对比如附录C 表C6 所示。由表可知：虽然传统HELM 能收敛，但由于幂级数初始点与真实潮流解偏差相对较大，计算速度较慢；相较于传统HELM，本文所提A-HELM 串行计算方法的自适应幂级数初始点更接近真实潮流解，因此，潮流收敛所需幂级数阶数更少，验证了所提A-HELM 串行计算方法具有较高的计算效率。

A-HELM 与传统HELM 初始最大功率不平衡量的对比如附录C 表C7 所示。由表可知：相较于传统HELM，采用所提A-HELM可有效减少系统功率不平衡量，这是由于传统HELM节点电压幂级数的初始值通常选取平启动方式下的电压幅值，而所提A-HELM根据系统节点导纳矩阵和平衡节点电压自适应调整节点电压的幂级数初始点，这使得节点电压幂级数初始点的电压值更加接近实际潮流解；相较于传统HELM，当系统节点数较少时，所提A-HELM 的优势不明显，其最大功率不平衡量未显著减小，而当系统规模变大，网络拓扑更复杂时，所提A-HELM 的优势凸显，其最大功率不平衡量明显减小。

为进一步分析幂级数初始点对潮流收敛的影响，图3 以Case 4gs、Case 300、Case 2 746wp、Case 3 012wp、Case 3 375wp、Case 10 790 测试系统为例，给出了A-HELM 与传统HELM 的系统最大功率不平衡量随电压幂级数阶数增加的变化趋势。由图可知：当系统规模较小时，A-HELM 与传统HELM 的收敛趋势较接近；随着系统规模的增大，A-HELM 的系统最大功率不平衡量均小于传统HELM。在潮流收敛过程中，传统HELM 的节点电压幂级数系数的初始点均固定为1+j0 p.u.，这使得潮流计算起始的系统功率不平衡量较大，进而影响电压高阶次幂级数系数的求取，导致求解过程中出现较大的收敛振荡。与传统HELM 相比，自适应初始点可减小A-HELM在计算初始时的潮流功率不平衡量，因此，减小了幂级数初始点对电压高阶次幂级数系数求解的影响。

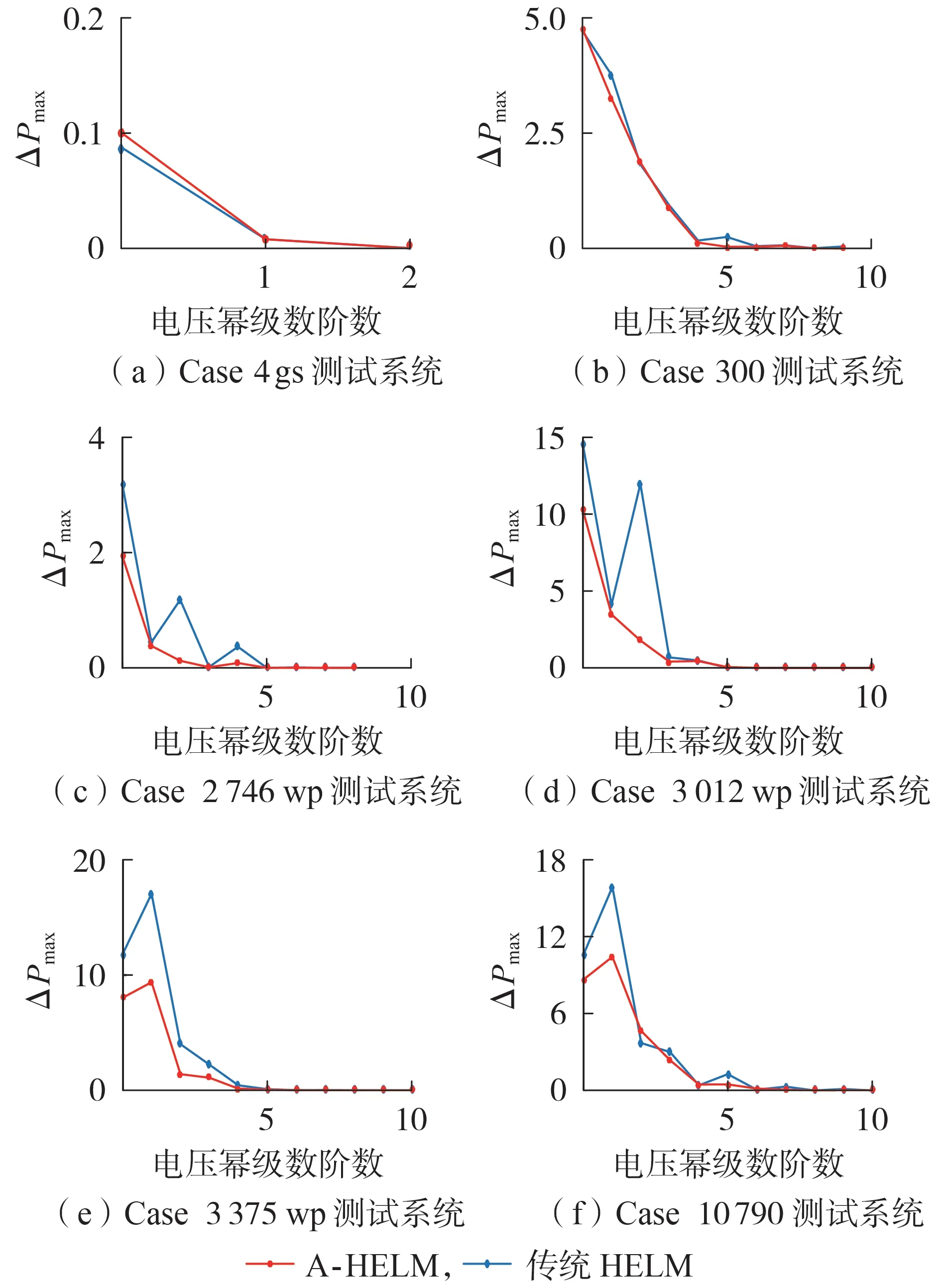
图3 不同测试系统中A-HELM与传统HELM最大功率不平衡量变化趋势对比Fig.3 Variation trend comparison of maximum power unbalance between A-HELM and traditional HELM in different test systems

由上述分析可知，与传统HELM 相比，A-HELM基于节点导纳矩阵和平衡节点电压自动生成更适用的幂级数初始点，使得A-HELM 的潮流收敛趋势更加平滑，从而减少了潮流收敛所需的电压幂级数阶数，因此，自适应幂级数初始点的选取方法使得AHELM比传统HELM具有更好的潮流收敛性。

3.3 计算效率对比

本节进一步验证所提A-HELM 串行计算方法和A-HELM 并行计算方法的计算效率。在内存需求方面，在求解全纯嵌入潮流模型的过程中，A-HELM 幂级数系数递归求解方程组的系数矩阵元素均为系统网络节点导纳值，在较大规模的实际算例中该系数矩阵占用内存的情况如附录C 表C8 所示。由表可知：该系数矩阵为常数矩阵且具有很高的稀疏度，因此，在编程时可采用稀疏格式存储矩阵，并以该格式进行科学计算；实际求解时，A-HELM 系数矩阵占用的内存略高于传统NR 法的雅可比矩阵占用的内存，但由于A-HELM 系数矩阵是系统节点导纳矩阵的一种变形，因此，在系统网络拓扑结构不发生变化时，该系数矩阵数值不变，相较于传统NR 法的雅可比矩阵，无须对该系数矩阵进行反复更新和存储。

A-HELM 串行计算方法、A-HELM 并行计算方法以及传统HELM 在求解不同规模测试系统时的潮流计算耗时对比如附录C 表C9 所示。由表可知：A-HELM 串行计算方法的计算耗时短于传统HELM的计算耗时，A-HELM 并行计算方法的计算耗时显著短于A-HELM 串行计算方法和传统HELM 的计算耗时；与传统HELM 相比，A-HELM 串行计算方法的计算效率平均提升28.86 %，其中，对于Case 2 746wp测试系统，A-HELM 串行计算方法的计算效率提升了40 % 以上。由于A-HELM 的幂级数初始点比传统HELM 更有利于潮流收敛，A-HELM 达到收敛所需电压幂级数阶数更低，计算量更小，缩短了整体用时，此外，A-HELM 简化了传统HELM 的算法逻辑，这使得求取每阶幂级数系数的耗时更短，从而在整体上提升了算法的计算速度。

为更直观地体现A-HELM 并行计算方法在求解电力系统潮流时的高效性，本文将A-HELM 串行计算方法的计算耗时与A-HELM 并行计算方法的计算耗时之比定义为加速比，加速比越大说明A-HELM并行计算方法的计算效率越高。表3 给出了不同测试系统潮流计算中的加速比。

表3 不同测试系统潮流计算中的加速比Table 3 Acceleration ratios in load flow calculation of different test systems

由表3 可知：对于不同规模的测试系统，加速比均稳定在4～5 之间，这说明A-HELM 并行计算方法具有较好的加速效果；测试系统规模越大，A-HELM并行计算方法的加速效果越明显，这是由于随着系统规模的增大，采用Padé 近似求解节点电压的总计算量也急剧增加，而对各节点电压Padé 近似的并行化可提升A-HELM 算法的计算效率，加快电力系统潮流的求解速度。