基于深度学习的直流配电网分布鲁棒优化调度方法

2023-11-11卫志农周亦洲孙国强

电力自动化设备 2023年10期

卫志农，徐昊，陈胜，周亦洲，孙国强

（河海大学能源与电气学院，江苏南京 211100）

0 引言

新型能源体系背景下［1］，电网中风电、光伏等新能源的大规模接入成为支撑其发展的重要举措［2］。然而，由于分布式电源出力的随机性和间歇性，配电网的消纳能力受到限制［3-4］，这给电力系统的安全稳定运行造成了巨大的威胁。相比于交流配电网，直流配电网一方面减少了交直流变换环节，提高了系统的转化效率，另一方面无须控制无功功率和频率，稳定性和可靠性更高，在处理分布式电源的不确定性方面具有较大优势［5］，便于光伏、储能等分布式电源的接入［6-7］。因此，开展直流配电网优化调度的研究具有重要意义。

准确刻画新能源不确定性是制定优化调度策略的关键［8］。当前常用于处理分布式电源不确定性问题的方法主要是随机规划［9］和鲁棒优化［10］。文献［11］基于历史数据获得可再生能源出力的概率密度函数，采用蒙特卡罗模拟来生成大量场景以处理清洁能源的不确定性。文献［12］在底层建立各设备模型，在顶层进行容量配置，构建了两阶段随机优化模型来确定系统在给定容量配置条件下的成本期望。但随机规划需假定随机变量服从某一种确定的分布，且需要大量的样本进行模拟，导致其效率偏低，调度结果缺乏鲁棒性［13］。鲁棒优化则在一定程度上改善了随机规划调度策略的鲁棒性。文献［14］建立了交直流配电网的二阶锥鲁棒优化模型，通过无功电压的控制策略来协调无功电压设备和交直流变电站，致力于寻找最优的鲁棒控制策略。然而，鲁棒优化完全忽略了不确定变量的概率分布信息，在最恶劣场景下进行调度决策，调度结果过于保守。

针对上述问题，分布鲁棒优化方法较好地结合了随机规划和鲁棒优化的特点［15-16］，在最恶劣概率分布下进行优化决策，以其优良的特性得到了广泛应用［17］。文献［18］构建了基于数据驱动的交直流配电网分布鲁棒模型，处理了分布式电源和负荷的不确定性。文献［19］在考虑配电网灵活性的基础上建立供需平衡的两阶段日内分布式优化调度模型，实现了对高渗透率分布式电源配电网的高效求解。文献［20］利用深度学习从历史数据中获取可再生能源出力的经验概率分布，构建基于分布鲁棒的网络重构模型。然而，上述基于场景的分布鲁棒模型求解过程复杂，需要反复迭代识别最恶劣概率分布，计算效率低。而对于未来高比例光储渗透的新型配电网，模型求解复杂度急剧上升，难以满足配电网实时决策调度的需求。因此，利用数据驱动类方法提高基于场景的分布鲁棒优化调度模型的求解效率，对保障电力系统的安全稳定运行具有重要意义。

为此，本文构建了基于深度学习的直流配电网分布鲁棒优化调度模型。首先，建立了传统的直流配电网基于场景的分布鲁棒物理模型，利用列与约束生成（column and constraint generation，CCG）迭代方法求解，以此生成大量的训练数据；其次，以光伏出力、负荷、范数置信度为输入，以最恶劣概率分布为输出，建立深度学习模型，采用生成的训练数据对深度学习模型进行训练；然后，根据实时输入的光伏出力、负荷、范数置信度，基于训练好的深度学习模型预测得到最恶劣的概率分布，构建最恶劣概率分布下的单层随机规划模型，获取等效的分布鲁棒优化模型的调度策略；最后，采用33 节点的直流配电网测试系统进行仿真，验证了深度学习的有效性。

1 直流配电网分布鲁棒优化调度模型

1.1 确定性直流配电网优化调度模型

1.1.1 目标函数

直流配电网确定性优化调度模型以系统运行成本最小为目标，具体如下：

式中：t为调度时刻；i为节点编号；T为总的调度时段（本文取24）；Ωsub为上级电网集合；为上级电网分时购电价格；Δt 为相邻调度时段间隔；为上级电网的购电功率；l 为储能编号；Ωess为储能集合；clt为储能充放电的成本系数；分别为储能的充电和放电功率；Npv为光伏机组数量；为弃光惩罚的成本系数；为弃光功率；Nbus为总节点数；η为切负荷惩罚系数；Pi，t，cut为切负荷功率。

1.1.2 直流支路潮流约束

基于二阶锥规划的直流支路潮流模型如下［21-22］：

式中：Ωdc为直流节点集合；Bdc为直流支路集合；Pi，t为注入节点的有功功率；vi，t为节点电压幅值的平方；Pij，t为流过支路ij的有功功率；lij，t为流过支路ij的电流的平方；rij为直流支路ij 的电阻；F(i)表示以节点i为首端节点的支路的末端节点集合；T(i)表示以节点i 为末端节点的支路的首端节点集合；为光伏注入的有功功率；为负荷功率。式（2）和式（5）为节点功率平衡约束，式（3）为二阶锥松弛后的支路容量约束，式（4）为支路电压降落方程。其余运行约束包括储能、光伏机组、上级电网购电、系统安全、切负荷约束，具体表达式见附录A。

1.2 数据驱动的分布鲁棒优化模型

为适应光伏出力的随机性和节点负荷的波动性，在1.1节确定性优化模型的基础上构建如下两阶段基于场景的分布鲁棒优化模型。将上级电网购电功率和储能的充放电功率作为第一阶段调度变量，其在获知光伏实时出力之前进行决策，不随实际场景变化而变化。将弃光量和切负荷量作为第二阶段调度变量，其在获知光伏实时出力之后进行决策，实时调整。

1.2.1 目标函数

考虑光伏出力不确定后的分布鲁棒优化模型如下：

式中： f1为第一阶段调度成本； f2，k为在第k个场景下的第二阶段调度成本；pk为第k 个场景发生的概率；K 为筛选得到的典型场景数；为第k 个场景下的弃光功率；Pi，t，k，cut为第k个场景下的切负荷功率。

1.2.2 模型约束

考虑光伏出力不确定后的分布鲁棒优化模型约束包含两部分。第一部分与1.1 节确定性模型的约束相同，包括直流潮流约束（式（2）—（5））、储能装置运行约束（式（A1）—（A7））、光伏机组约束（式（A8）、（A9））、上级电网购电约束（式（A10））、系统安全约束（式（A11）、（A12））和切负荷约束（式（A13））。第二部分是综合范数的约束条件。理论上，离散场景的初始概率取值的可行域Ω 为任意范围，但为了更加符合实际情况，本文构建了以初始概率分布为中心、1-范数和∞-范数为约束条件的不确定概率分布集合Ω，如式（9）所示。

式中：θ1、θ∞分别为1-范数和∞-范数允许的概率偏差限值；pk0为第k个场景下的初始概率值。

根据文献［23］，参数θ1、θ∞的计算方式如下：

式中：M 为历史总样本数；α1、α∞分别为1-范数和∞-范数的不确定概率置信度。

1.3 模型求解

综上，由1.2.1节和1.2.2节构成的基于场景的分布鲁棒模型的通用形式表达如下：

式（12）—（16）所构建的是一个min-max-min 的3 层优化问题，与传统的鲁棒优化仅仅优化最恶劣情况下的调度策略不同的是，基于场景的分布鲁棒致力于求解决策变量{pk}，获得K个典型场景的最恶劣概率分布情况，以此来求得期望成本的最大值。

采用CCG 算法求解基于场景的分布鲁棒模型，其将模型分解为主问题和子问题迭代求解。主问题在子问题识别的最恶劣概率分布下求解满足所有约束条件的最优第一阶段调度决策，提供模型的下界值U1，主问题如下：

式中：ψ为替代第二阶段调度成本的辅助变量；m为迭代次数；n为迭代次数上限为经m次迭代后求解得到的第k个场景下的最恶劣概率分布；为第m次迭代之后的第二阶段调度变量值。

子问题是在主问题求得的第一阶段调度策略下，识别最恶劣的概率分布，提供给主问题进一步迭代计算，并提供模型的上界值U2，子问题如下：

由于子问题（式（23）—（26））中内层优化的第一阶段调度变量及各典型光伏场景的出力均已知，内外层优化变量在约束中无耦合，因此可以进一步拆分为式（27）和式（28）所示的2个模型单独求解。

利用CCG 迭代的方式求解基于场景的分布鲁棒模型步骤见附录B［24］。

2 基于深度学习的直流配电网分布鲁棒调度方法

第1 章中构建的分布鲁棒优化模型需要进行反复迭代来识别最恶劣的概率分布，获取最恶劣概率分布下的最优调度决策，其求解时间长、效率低。因此，本文采用基于深度学习的方法辅助求解，替代分布鲁棒优化的迭代求解过程。将第1 章分布鲁棒模型输入参数中的光伏出力、负荷、范数置信度作为输入，将输出参数中的最恶劣的概率分布作为输出构建深度学习模型，直接对典型场景的最恶劣概率分布进行预测。然后，根据预测得到的最恶劣概率分布构建单层随机规划模型获取等效的分布鲁棒调度决策。

基于深度学习的直流配电网分布鲁棒调度方法包括深度学习模型的构建、训练样本生成以及基于深度学习预测结果的单层随机规划模型构建三部分。

2.1 深度学习模型构建

基于上述分析，本文构建的深度学习模型以光伏出力、系统负荷、范数置信度为输入，以典型场景的最恶劣的概率分布为输出，具体如下：

式中：I为模型输入；O为模型输出。

采用ReLU 函数作为深度学习模型的非线性激活函数，函数表达式如下：

式中：φ为上层神经元的输出；f(φ)为下一层神经元的输入。

因此从输入到输出的映射可以采用如下的方式表达：

式中：u0为初始输入；rz、uz分别为隐藏层z的线性映射和激活函数的输出；Z为隐藏层集合；|Z|为隐藏层数；W、ρ分别为需要通过训练学习的权重和偏差。此外，因为输出为概率分布，需满足以下约束：

本文采用Adam 算法对深度学习模型进行训练。具体过程为在前向传播中计算输入的乘积和对应的权重，利用激活函数作用于这些乘积的总和，通过在神经网络的反向传播中回传相关误差，计算损失函数及其对于各个参数的梯度，更新权重参数W和偏置参数ρ，实现对模型的训练。

选用均方误差δMSE作为损失函数，计算公式如下：

式中：yi为实际值；为预测值；N为总样本数。

Adam算法的权重更新公式如下：

式中：φt为待更新的Adam 算法权重；δ为学习率；μ为平滑参数；分别为经过误差修正后梯度的平均值和方差，具体的计算公式如式（39）所示。

式中：ϑt、τt分别为梯度的平均值和方差；σ1、σ2为衰减因子。

选用平均绝对误差δMAE和决定系数δR2作为深度学习模型的评价指标，判断模型的可行性，其计算公式分别如下：

式中：yˉ为真实值的平均值。

2.2 训练样本生成

2.2.1 光伏出力

基于光伏出力历史数据，考虑一定程度上的光伏出力波动，服从正态分布N(1，(σpv)2)，其中σpv为光伏出力波动标准差，具体如下：式中：Ppv0，i，t为光伏机组的预测出力。

2.2.2 负荷需求

采用正态分布N(，(σL)2)模拟负荷的变化，其中为系统负荷功率均值，σL为负荷波动标准差。考虑负荷的季节性变化，抽样时和σL是随机变化的，但在一个月内认为其是保持不变的。

2.2.3 范数置信度

1-范数和∞-范数均为服从［0.2，0.99］区间内均匀分布的随机数。

根据第1 章构建的分布鲁棒模型，采用CCG 算法迭代求解，记录每一次输入的光伏出力、负荷、范数置信度和对应输出的典型场景最恶劣概率分布，进而构成深度学习模型的训练和测试样本。

2.2.4 样本筛选

为保证样本的准确性，需要对样本进行筛选，筛选条件如式（44）所示，将不收敛样本剔除。

式中：ε为迭代收敛精度。式（44）表示分布鲁棒模型的上下界需要满足收敛条件，概率分布之和严格为1，否则将该不可行样本踢除。

2.3 最恶劣概率分布下的单层随机规划模型

根据实时输入的光伏出力、负荷、范数置信度，基于上述训练好的深度学习模型预测得到最恶劣的概率分布，将1.2节分布鲁棒优化模型中的概率分布直接固定为预测获取的最恶劣概率分布，即可将式（12）—（16）所示的3 层分布鲁棒模型转化为式（45）—（49）所示的最恶劣概率分布下的单层随机规划模型。

综上所述，基于深度学习的直流配电网分布鲁棒调度框架如附录C图C1所示。

3 算例分析

3.1 算例参数

本文选取33 节点的直流配电网系统进行测试，系统结构和参数见文献［25］，系统中的负荷功率预测值和光伏典型场景出力如附录C 图C2所示，储能装置的相关参数如附录C 表C1 所示。本文算例在处理器为2.8 GHz、内存为16 GB 的台式计算机上采用GAMS24.8.2，调用GUROBI求解器进行求解。

3.2 光伏历史场景的获取及训练样本生成

由于难以获取大量的光伏历史数据，本文以光伏预测值为期望，以0.5 为方差，采用正态分布的方式随机生成500 个光伏出力场景，并赋以10 %～20 %的波动，采用K-means 聚类方法，通过求解每一类场景的数量得到其概率值。

为保证训练样本的普适性和多样性，本文选取一个月的光伏出力和负荷数据作为输入，在GAMS平台调用GUROBI 求解器进行求解，记录物理模型的输入和输出的结果生成训练样本，用于在Python平台构建深度学习模型。

3.3 深度学习模型设置

深度学习模型是在Python 平台上设计的，该模型分别由10个神经元的输入层，1 024、512、256个神经元的隐含层和10 个神经元的输出层的全连接神经网络构成，采用的激活函数为ReLU。另外，整个模型采用Adam 优化器，损失函数为δMSE，将最大学习次数和学习率分别设为300 和0.01，批量大小设为128。整个模型在处理器为2.8 GHz、内存为16 GB的台式计算机上运行，运行时间为132 s。

3.4 深度学习辅助有效性分析

经过筛选，共得到10 000个有效的训练样本，以8∶2 的比例划分为训练集和测试集，调用Python 平台的keras 模型进行训练，最终通过训练计算得到δMSE=2.0×10-5、δMAE=2.5×10-3、δR2=0.989。

3.4.1 物理模型与深度学习模型优化调度效果对比

随机选取4 个样本的最恶劣概率分布的预测值与真实值的对比如图1所示，误差对比如表1所示。

表1 各样本误差对比Table 1 Error comparison of samples

图1 预测值与真实值的对比Fig.1 Comparison between prediction values and true values

由图1 和表1 可知，随机抽取的4 个样本的预测值和真实值的最大相对误差为0.064，平均相对误差为0.018。这意味着深度学习预测得到的最恶劣概率分布与基于场景的分布鲁棒模型求得的最恶劣概率分布之间的误差较小。为了比较两者在调度成本和计算时间方面的差别，将原始基于场景的分布鲁棒模型转化为最恶劣概率分布下的单层随机规划模型，其调度成本和计算时间的对比如表2所示。

表2 物理模型和深度学习模型效果对比Table 2 Comparison of effects between physical model and deep learning model

由表2 可知，通过深度学习预测得到的调度成本与实际相比的误差小于10-3数量级，但是计算效率能提高4～5 倍，计算速度大幅加快的同时也保证了预测结果的精确性，基本满足优化调度的要求。

3.4.2 样本数对深度学习模型的影响

本节对不同样本规模下深度学习模型的训练效果进行了对比分析。不同样本数下深度学习模型的训练效果如表3 所示，并随机选取一组未参与训练的样本对不同样本数训练下深度学习模型的预测精度进行对比，不同样本数训练下得到的深度学习模型的预测效果如表4所示。

表3 不同样本数下的模型效果对比Table 3 Comparison of model effects under different sample numbers

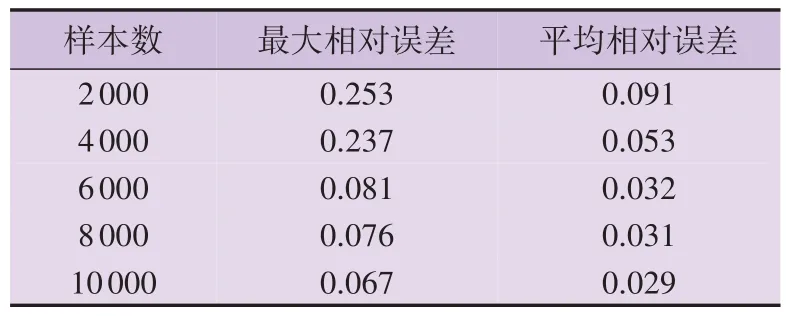
表4 不同样本数下的预测效果对比Table 4 Comparison of prediction effects under different sample numbers

由表3 可知，随着样本数逐渐增加，深度学习模型的δMSE和δMAE逐渐减少，δR2逐渐增大，说明样本数越多，深度学习模型对数据的拟合程度和精度越高。当样本数达到8 000 以上时，拟合程度逐渐趋于饱和，此时继续增加样本数，对深度学习模型精确程度的影响逐渐减小。这是因为通过更多样本的学习，数据中的特征信息能够更好地融合，神经网络在反向传播时的误差也就越小，各个权重参数和偏置参数更加精确，此时深度学习模型已经学习到足够精确的参数，而当样本数继续增加时，由于样本是在一定范围内变化的，之前的样本数已经足以学习到样本数据特征的分布规律，所以进一步增加样本数对模型精度的影响会逐渐减小。由表4 可知，随着样本数增加，预测样本的最大相对误差和平均相对误差都随之减小，模型更加精确，也进一步验证了表3的结论。

3.4.3 光伏历史场景数量对深度学习模型的影响

本节通过改变光伏历史场景数量来验证其对深度学习模型的影响。设置α1=0.5、α∞=0.9，取典型场景数量K=10。光伏历史数据取100～10 000 进行计算，结果如附录C 图C3 所示。由图可知，随着光伏历史场景数据的增加，各类总成本减少，并且逐渐接近，这是因为历史数据的增加使得概率分布允许偏差限值减小，从而降低了求解问题的保守度。通过对比发现，不论历史数据量是多少，总成本大小依次为1-范数、∞-范数、综合范数，这是由于1-范数约束通过限制所有典型场景概率的总体偏移程度控制模型的保守性，∞-范数约束通过限制各个典型场景概率的最大偏移程度控制模型的保守性，在不同程度上都存在着一定的片面和极端情况，而综合范数约束与获得的实际运行数据更加贴切，且保证其在合理的范围内波动，所以保守性有一定程度的降低。

3.4.4 不同置信区间对深度学习模型的影响

通过设置不同的置信度α1和α∞来比较深度学习模型的预测结果，计算得到每次的调度总成本。设历史数据个数M均为1 000，聚类后的离散场景K均为10，结果如附录C 表C2 所示。由表可知，随着α1、α∞的增加，θ1和θ∞的值随之增加，总成本值也随之增加。这是因为若置信度增加，则置信区间增大，所包含的不确定性增大，需要更多出力。值得注意的是，当α∞=0.2 时，不论α1取0.2、0.5 还是0.9，总成本都不变；同样地，当α∞=0.5 时，不论α1取0.5 还是0.9，总成本都不变。所以可以得出如下结论：当α1＞α∞时，调度成本与α1=α∞时一致。原因是当α1取值较大时，1-范数约束条件对概率置信集合的确定不起约束作用，只有∞-范数起约束作用。