转向架非主体结构件模态频率规划与设计验证

2023-11-10沈龙江陈国胜钟晓波李家琛

铁道机车车辆 2023年5期

沈龙江，秦烺，陈国胜，钟晓波，李家琛

（1 大功率交流传动电力机车系统集成国家实验室，湖南株洲 412001；2 中车株洲电力机车有限公司，湖南株洲 412001）

随着轨道车辆结构强度方面的研究日益深入，模态分析、匹配和规划越来越多地成为研究的重点，而这些研究主要集中于车体、构架、轮对等主体结构，例如机车车体和转向架模态分析研究［1］、地铁车辆转向架构架模态匹配方法研究［2］、基于模态分析的列车轮对结构优化研究［3］等。而文中的研究对象是转向架非主体结构件，例如天线、扫石器、撒沙、轮缘润滑、脚蹬、管线等设备的安装支架。这些部件需要满足多样化的功能需求，但一般没有单独的设计标准，通常依据EN 13749-2011［4］标准中定义的安装于构架或轴箱上部件振动加速度载荷进行强度计算，但是该定义是基于准静态的方法，忽略了模态频率共振因素，然而近年来大量失效案例表明，共振是引起工程结构失效的重要原因，且多数表现为疲劳形式［5］，而共振疲劳与结构固有模态频率、轮轨激振频率密切相关［6］，这就说明对转向架非主体结构件的模态频率规划是缺失的，有必要开展深入研究。

另外，为了验证上述模态频率规划是有效的，有必要开展模拟实际运行载荷频谱的随机振动试验，在此过程中可以不断地优化和验证转向架非主体结构件特别是悬臂件的可靠性［7］。 IEC 61373-2010［8］标准中的功能振动试验量级对应的是未经加速度比例系数放大的运行数据，但这些运行数据来源于欧洲轨道车辆，该标准中定义的振动功率谱幅值和频率范围与国内车辆实际服役条件仍存在一定的差异，故有必要结合国内线路实测振动频谱分析转向架非主体结构件振动试验量级。为了提高设计验证效率，还有必要进行仿真计算，文中将结合示例进行分析。

1 模态频率规划研究

文中梳理了来自轮轨系统的激振频率并与IEC 61373-2010［8］的随机振动试验频率范围进行对比，主要包括车轮多边形频率、钢轨波磨频率、轨枕通过频率、P2 共振频率等多方面，其中前两者是车辆在轨道上运行一段时间之后可能会产生的，而后两者属于车辆与轨道系统的固有频率。

1.1 车轮多边形频率

车轮多边形表现为车轮周向磨耗不均，往往有一个主导阶数（危害最大），给定车速下其对应多边形主导通过频率。车轮多边形会持续激发轮轨界面固定频率的振动，其频率为式（1）：

式中：f1为频率；v1为速度；n为多边形阶数；L为车轮周长。

例如某地铁在轮径0.83 m、5 阶多边形、60 km/h 工况下的激振频率为32 Hz，某机车在半磨耗轮径1.2 m、24 阶多边形、100 km/h 工况下的激振频率为177 Hz。作为对比，根据高速动车组线路试验数据，在不同车辆、不同轮径、不同踏面状态的情况下，产生车轮多边形磨耗的转向架轴箱振动中出现了接近的频率，即550~650 Hz 附近的振动主频［9］。

若已发现车轮多边形问题，可以根据车轮直径范围、多边形主导阶数、车辆主要运行速度范围等情况分析多边形激振频率范围。

1.2 钢轨波磨频率

钢轨波磨是沿钢轨纵向接触表面出现的周期性不平顺现象，在不同的铁路系统均有出现［10］。根据我国地铁线路调查，在不同的波磨特征、轨道结构形式和运营条件下，钢轨波磨通过频率范围可达50~840 Hz［10］。该频率与波长、车辆通过速度相关，钢轨波磨激振频率为式（2）：

式中：f2为钢轨波磨激振频率；v2为速度；λ1为波长。

设车速为71 km/h，若轨道波磨长度为230 mm，则激振频率约为85 Hz；若波磨长度为30 mm，则激振频率约为657 Hz。

若已发现钢轨波磨问题，可以根据钢轨波磨的波长、车辆在波磨区段的主要运行速度范围等情况分析钢轨波磨激振频率范围。

1.3 轨枕通过频率

轨枕通过频率与轨枕间距、车辆通过速度相关，轨枕通过频率为式（3）：

式中：f3为轨枕通过频率；v3为速度；λ2为波长。

可以根据车辆主要运行速度范围分析轨枕通过频率范围。例如轨枕间距L为0.6 m，最高运行速度为120 km/h 情况下，最高轨枕通过频率为55.6 Hz，而速度160 km/h 对应74 Hz，速度350 km/h对应162 Hz。

1.4 P2 共振频率

P2 力是车辆通过轨道低接头、焊缝的时间历程中产生轮轨冲击力的第2 个峰值，是簧下质量和轨道质量在轨道弹性系统中振动所引起的响应力，频率一般在30~100 Hz 之间，持续时间较长［11］，故对轨道车辆系统影响较大。P2 共振可能导致低阶车轮多边形［7］。

设m为簧下质量+局部轨道段质量+轨枕质量，k为轨道垂向刚度，则频率近似计算为式（4）：

1.5 轮轨激振频率与随机振动试验频率的对比

IEC 61373-2010［8］是针对轨道车辆设备进行随机振动试验的标准，其中针对构架或车轴上安装设备的试验频率范围是：构架上为2~250 Hz；车轴上为10~500 Hz。与轮轨激振频率对比见表1，可见随机振动试验可以覆盖轨枕通过和P2 共振频率范围，不能完全覆盖车轮多边形和钢轨波磨频率范围。虽然标准中的频谱曲线也可以通过延长6 dB/倍频程衰减线延伸到更高频率，但延伸段对应的加速度谱密度是逐渐衰减的。

表1 轮轨激振频率与随机振动试验频率对比

1.6 模态频率优化分析

在转向架非主体结构设计时应进行模态分析和优化，使其固有频率尽可能避开表1 中的轮轨激振频率范围，具体而言：

（1）对于车轮多边形和轨道波磨频率，由于其频率跨度范围很广，需要首先搜集实际线路主激振频率，然后计算出结构多阶模态频率，若存在频率重合则需要调整结构和迭代计算，一般可选的频率间隔参考系数为优选=1.414（参考TB/T 3115-2005［12］中要求车体一阶弯曲自振频率与转向架的点头和浮沉自振频率的比值应大于1.4倍），次选=1.19。

（2）根据经验建议构架上结构件的一阶模态频率有效高于100 Hz，则可以避开P2 共振频率、160 km/h 以下车辆的轨枕通过频率等轮轨系统固有频率；建议轮对上结构件的一阶模态频率有效高于250 Hz，这是以表1 中典型车轮多边形频率177 Hz 的1.414 倍为边界，从而规避了主要的轮轨激振频率，这对所有车辆转向架都是有意义的。

（3）一般结构刚度的大小与模态频率的高低正相关，故为了改变结构的某阶次模态频率，可以从改变该阶次模态振动方向的刚度着手。

2 试验与仿真研究

2.1 线路振动测试

选取国内某120 km/h 地铁转向架上的天线梁开展了正线全线振动测试。由于该车辆的车轮存在12~13 阶多边形（部分小曲线路段还存在短波轨道波磨），故该测试分为车轮旋修前和旋修后两组，通过数据分析得到了纵向、横向和垂向振动加速度功率谱密度并与标准对照如图1~图3 所示。

图1 天线梁纵向加速度频谱

图2 天线梁横向加速度频谱

图3 天线梁垂向加速度频谱

由于IEC 61373-2010［8］功能振动试验量级取的是运行数据中的平均量级加上标准偏差，故在图1~图3 中主要针对实测的均值曲线与标准曲线进行对比，结论如下：

（2）在高于标准试验频率的250~1 000 Hz 频段（图中对标准频谱曲线进行了延伸），实测仍然存在一定的振动量级，甚至存在较高的峰值。

（3）在车轮旋修前，天线梁的振动加速度功率谱密度在纵向和垂向上明显高于标准，特别是在30~150 Hz 频段。

（4）在车轮旋修后，振动量级有所降低，部分频段的实测均值低于标准。

（5）实测与标准载荷谱的差异很大，对于新车或线路条件较好情况可以采用标准载荷谱，若车轮多边形等异常则建议采用实测载荷谱。

上述车轮旋修前的实测振动量级可以作为存在车轮多边形或轨道波磨等轮轨激振频率情况下的代表，说明此时转向架非主体结构件的服役边界条件比标准更为恶劣；而车轮旋修后消除了车轮多边形的影响，虽然仍存在轨道波磨，振动量级降低到了标准范围之内，说明车轮多边形对振动量级的影响很大。

2.2 基于线路实测数据的试验和仿真

为了检验转向架非主体结构件的振动疲劳强度，主要开展模拟长寿命振动试验。根据IEC 61373-2010［8］，为了缩短试验时间，试验量级需要基于功能振动量级放大β倍（β为加速度放大系数，基于该标准中的疲劳曲线推导，构架上β=5.66；车轴上β=3.78）。由于试验量级r.m.s. 值等于相应ASD 谱面积的平方根如图4 所示，故对每一个实测ASD 频谱对数坐标（f，ASD），可以按（f，β2×ASD）开展模拟长寿命试验，标准试验持续时间为纵向、横向和垂向各5 h。

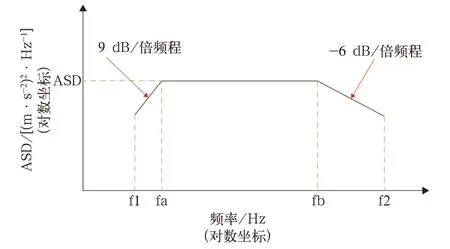
图4 ASD 频谱

采用Workbench 的仿真计算方法如图5 所示，必须首先完成Modal 模态计算，然后将Random Vibration 计算与Modal 关联，选取约束条件和振动频谱的方向，输入上述对数坐标（f，ASD）或（f，β2×ASD），完成等效应力计算。

均衡在摄影创作中的应用……………………………………………………………………………………………李强（1.63）

图5 Workbench 振动仿真计算示意图

2.3 放大的试验量级

若已知存在车轮多边形等更加恶劣的服役边界条件，但没有线路实测数据，则需要一种放大的试验量级用于试验、仿真及结构优化。实际上对比IEC 61373-1999［13］与IEC 61373-2010 这2 个版本可知，其采用的线路实测数据相同但加速度放大系数计算方法不同，IEC 61373-2010 版基于典型金属材料的疲劳寿命曲线考虑了时间截止极限，而IEC 61373-1999 版本中放大系数完全与运营寿命和试验时间之间的比例正相关，故计算得到的加速度放大系数β更大（为7.83，不区分构架上或车轴上），故模拟长寿命振动试验量级更大。另外该标准中考虑的部件使用寿命为25 年，若提高到目前普遍要求的车辆使用寿命30 年，则β将进一步提高到8.19，由此得到的模拟长寿命振动试验量级与IEC 61373-2010［8］标准对比见表2。

表2 一种放大的模拟长寿命振动试验量级与标准对比

3 模态优化和仿真示例

3.1 示例说明

一种L 型板管夹座开裂问题如图6 所示，为了解决该问题考虑采用C 型槽代替L 型板作为管夹座，2 种方案对比如图7 所示。

图6 管夹座开裂问题

图7 2 种管夹座方案对比

3.2 仿真计算对比

为了验证优化方案的可行性，进行了模态计算和基于IEC 61373-2010［8］的模拟长寿命振动仿真计算，结果对比见表3，如图8 所示。

图8 2 种管夹座振动强度仿真对比

表3 2 种管夹座方案计算对比

通过上述对比可知，原方案模态频率偏低，容易与表1 中的轮轨激振频率产生共振，故不符合文中的模态规划要求，另外模拟长寿命振动仿真应力偏大，尤其是Z向最大应力位于焊缝附近，仿真验证不通过；而优化方案的模态频率较高，且远远超出了IEC 61373-2010［8］随机振动试验的载荷频率范围，相应的模拟长寿命振动仿真应力也很小，仿真验证通过。