基于振动的机车轴箱轴承故障诊断

史 鸣，潘长领，许自强

（1 洛阳市轨道交通集团有限责任公司，河南洛阳 471000；2 郑州地铁集团有限责任公司，郑州 450003；3 中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081）

滚动轴承在旋转设备中起着至关重要的作用，其工作状态直接影响到整台设备的运行。据调查，在应用滚动轴承的机械设备中，其造成的故障占比约为30%。每年我国因为滚动轴承异常而诱发的列车故障都会造成较大损失，严重影响人们生命财产安全。国内对于滚动轴承故障检测起于20 世纪80 年代，主要的检测手段有轴温检测、振动信号检测、Fourier Transform、BP 神经网络、Empirical Mode Decomposition 等。一些机构分别研发了轴温报警装置，采取在轴承轴箱上加装温度传感器来完成对轴承故障状态的诊断［1］。轴承运行早期发生微弱故障时，其温度与正常轴承温度近乎相同，只有故障严重到一定程度才会引起轴温明显上升，因此，该方法在故障发展早期不适用。某大学采用振动分析法研发的滚动轴承自动检测系统JK864n，以共振解调技术为核心，借助装配在轴承座的电子传感器对轴承振动信号进行采集分析，完成轴承故障诊断［2-3］，该方法具有检测精度高、诊断效率快及投资成本低等特点，比较适用于轴箱轴承的诊断维修，但如何设置带通滤波提升信噪比对故障检测结果的可靠度具有重要影响。

文中从滚动轴承故障机理入手，提出了基于峭度值、小波分析、Hilbert 包络谱分析的方法来对滚动轴承进行故障诊断［4］。首先利用峭度值对轴承状态做整体判断，其次根据小波变换可以从杂乱无章的信号中进行消噪提取出有用信号的特点，阐述了小波去噪的步骤和方法，并将峭度值、小波分析、Hilbert 包络谱分析3 者结合用于实测滚动轴承外圈和内圈的故障诊断当中，效果理想［5］。文中主要特点一是利用小波进行降噪，克服了大量噪音给直接应用Hilbert 包络谱分析造成的干扰，大大提高工作效率及诊断可靠性；二是利用Hilbert包络谱分析进一步确定故障特征频率，准确识别故障与位置。

1 滚动轴承故障机理及特征频率

1.1 故障机理

一般情况下，造成轴承振动的内部因素主要有运行缺陷、构造特性及制造偏差等，外部因素主要指轮对传动轴上其余零部件之间的相互作用，在这2 种因素共同施加下，轴在外界施加的强度及负荷下运转时，会引起轴承及其总成系统的振动。在这一整体振动中，不考虑轴承内部构造特性和制造偏差，文中主要研究运行缺陷对整个系统所造成的影响。滚动轴承的工作环境比较复杂，故障信号不可避免被掺杂噪音，怎样从采集到的振动信号中将噪音筛除，突出显示由运行缺陷导致的振动信号是文中轴承故障诊断的关键环节［1］。

1.2 故障特征频率计算

滚动轴承主要由轴承内外圈、滚动体、保持架等部分组成。各部分的故障特征频率计算方法式（1）~式（4）［6-7］：

内圈故障特征频率：

外圈故障特征频率：

滚动体故障特征频率：

保持架故障特征频率：

式中：D为滚动轴承的节圆直径；n为滚动轴承的转速；d为滚动轴承滚动体的直径；z为滚动轴承滚动体的个数；α为滚动轴承的接触角。

2 小波技术在故障诊断中的应用

2.1 小波去噪

小波分析可以处理Fourier 变换不能有效处理非平稳信号的难题，滚动轴承实际工作时，不可避免受到外界环境噪声干扰，振动信号中冲击成分含量较高，因此探索一种能消除噪音干扰，加强振动信号中故障成分，有效提取振动信号故障特征的分析手段十分必要［8-9］。小波分析不仅能提供较强的时间分辨率，在频域也有较强的定位能力，还能克制信号干扰，较好处理复杂的非稳态信号。小波技术去除噪音流程如图1 所示。

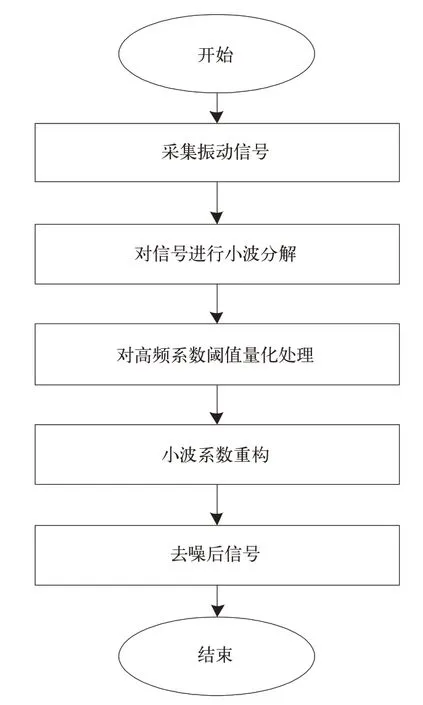
图1 小波技术去除噪音流程

在去除噪音步骤中，第3 步阈值的选取是小波技术降噪流程中的重点，阈值选择未达到最优将会对信号降噪的效果产生不利影响。一般地，小波分析进行去噪处理常见的有3 种方法［1］：

（1）默认阈值降噪法

主要应用了ddencmp 及wdencmp 这2 个函数，ddencmp 负责获得振动信号的默认阈值；wdencmp主要用来对小波实施降噪处理。

①ddencmp 函数

使用方法为［THR，SORH，KEEPAPP，CRIT］=ddencmp（IN1，IN2，X）。其中，参数X为振动信号，IN1 取值’den’或’cmp’，去噪用’den’，压 缩用’cmp’；IN2 取 值’wv’或’wp’，选 择 小 波 时用’wv’，选择小波包时用’wp’。THR 为返回阈值；SORH 为软、硬阈值选择参数；KEEPAPP 为保存处理信号；CRIT 仅在小波包时使用表示熵名。

②wdencmp 函数

主 要 使 用 方 法 为［XC，CXC，LXC，PERF0，

PERFL2］=wdencmp（’S’，X，’wname’，N，THTR，SORH）；wname 为所用的小波函数，S 取值为’gbl’或’lvd’，’gbl’为采用相同阈值处理所有层信号，’lvd’为用不同阈值分别处理不同层，N 取值为小波分解的层数，XC 为将要去噪的信号，［CXC，LXC］即XC 的 小 波 分 解 构 造，PERF0 及PERFL2 用百分比表示去躁所保留的能量成分。

（2）给定阈值降噪法

在实际工作中，采用wthresh 函数，借助经验公式，得出小波降噪的最佳阈值，该法可靠性较高。wthresh 函数使用方法为y=wthresh（X，SORH，T）；y 为生成的线信号，T 即THR，指阈值；SORH取值’s’为软阈值，SORH 取值’h’为硬阈值，计算软硬阈值时：ythard=wthresh（y，’h’，thr），ytsoft=wthresh（y，’s’，thr）。

（3）硬性降噪法

又称强制降噪法，即采用一刀切的方式去除小波分解后的所有高频成分，该方法操作简单方便，但极易造成振动信号中的有用成分丢失。

文中是在MATLAB 语言下进行小波信号分析与处理，主要利用离散小波的分解与重构实现对采集信号的去噪处理。下面介绍小波去噪等方法的MATLAB 函数［10］。

MATLAB 中实现小波分解的函数是wavedec，指令：［C，L］= wavedec（X1，N，’wname’），其中，X1 为振动信号；N 取值为正整数，代表尺度；wname 为小波名字。

小波分解后需要重构振动信号，MATLAB 中实现小波重构的方法：X1=wrcoef（’type’，C，L，’wname’），type 为对分解后的振动信号进行重构，type 取值为自然数，可以用d 表示。

比 如：［c，l］= wavedec（X0，4，’db4’）；即 对振动信号X0 用db4 小波进行4 层分解；

d4=wrcoef（’d’，c，l，’db4’，4）；

d3=wrcoef（’d’，c，l，’db4’，3）；

d2=wrcoef （’d’，c，l，’db4’，2）；

d1=wrcoef（’d’，c，l，’db4’，1）；

即对分解后信号进行重构，给d1，d2，d3，d4赋值。

2.2 结合峭度值、小波分析和Hilbert 包络谱分析的研究方法

（1）推算峭度值：首先通过公式推算出峭度值K，并初步诊断滚动轴承是否发生了早期故障（正常运行的轴承峭度值约为3），出现故障时需要对信号做进一步故障分析，为式（5）：

式中：xi为振动信号瞬时振幅值；p(x)为振动信号幅值的概率密度函数；μ为振动信号振幅均值；σ为振动信号的标准差。

（2）小波分解重构系数：精选合理的小波基对目标振动信号进行小波分解，以便得到各层低高频信号，而后去掉噪声干扰，再重新构造每层的信号。

对于给定信号，小波包尺度函数与小波函数为式（6）：

式中：尺度函数μ0(x)为信号的低频特性；小波函数μ1(x)为信号的高频特性；h(k)为高通滤波器；g(k) 为高通滤波器，进行多层小波包分解时［11］，为式（7）：

式中：i=0，1，……

小波重构算法为式（8）：

式中：n=2i，j∈Z，d为小波包系数。

（3）Hilbert 变换包络谱分析：对重构后的轴承信号做Hilbert 包络并进行谱分析，进一步判断故障情况。Hilbert 变换能够将轴承的振动信号转换成解析信号，转换后的信号由实、虚2 模块构成，其中前者指振动信号本身，后者指振动信号HiLbert 变换的结果［12］。实际振动信号的包络值即转换后解析信号的振幅值，其次再借助Fourier Transform 对包络信号进行处理，最终获得包络谱。

设(t)是任一时间序列g(t)的HiLbert 变换，表达式为式（9）：

g(t)的解析信号z(t)可表示为式（10）：

包络信号a(t)为式（11）：

3 故障试验

现有某车车轴箱轴承197726 型双列圆锥滚子轴 承，滚 子 数：21；接 触 角：7.666 7°；滚 子 直 径：27.74 mm；中径：186.626 mm；主要试验数据见表1。试验采用3 个轴承，分别编号I、II、III 号，其中I号轴承是外圈故障、II 号轴承是内圈故障、III 号是正常轴承。3 个轴承的时域波形如图2 所示。峭度计算结果如图3 所示。

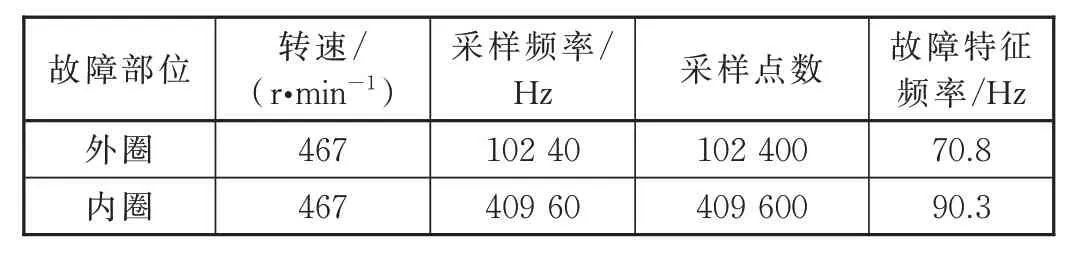
表1 实验数据

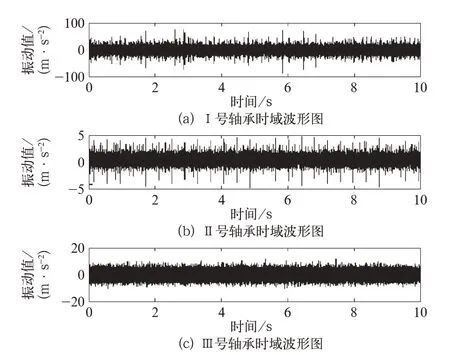
图2 3 个轴承的时域波形图

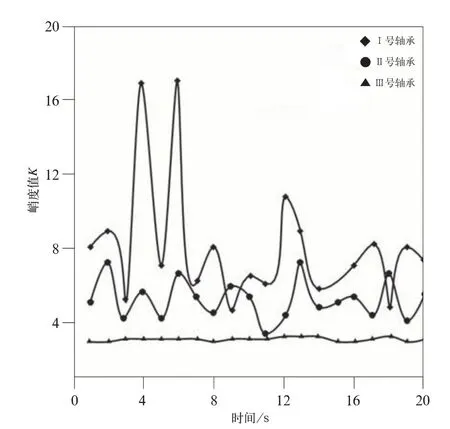
图3 峭度值计算结果

由峭度值计算结果可以看出，I、II 号轴承峭度值变化较大，远超出正常范围，III 号轴承的峭度值约为3，在正常范围内。在滚动轴承故障检测中，峭度值K作为加速度的参考量，也就是说峭度值K取值只能代表故障变化的快慢程度，并不能反应故障的大小，因此峭度值K在检测轴承故障状态是否变化方面十分灵敏。在滚动轴承故障发生的初期，故障一般呈上升趋势急剧变化，故峭度值显著增大，但故障发展到一定程度不再变化时，峭度值也不再变化。因此，峭度值应结合其他参数共同使用，不能单独作为评判指标。

时域波形图中，III 号正常轴承振动信号幅值较小，且无明显周期性毛刺谱线；而I、II 号故障轴承，谱线图中均存在明显冲击，包含较多杂音，且无法判断出内圈故障还是外圈故障。为进一步确定故障具体情况，消除振动信号中噪声干扰，突出显示信号有用成分，文中对I 和II 号再实施小波分解及重构。先对I 号轴承的振动信号进行各层离散，文中多次对数据仿真后选取以db4 为小波集合体，然后采用wrcoef 函数对振动信号实施二次组合，I 号故障轴承小波离散及重组后的振动信号如图4 所示［1］。

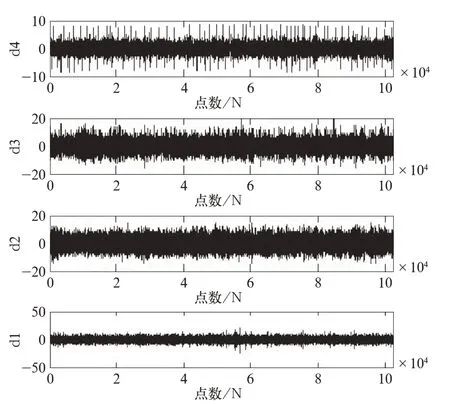
图4 Ⅰ号滚动轴承离散小波处理细节信号

由图4 中可知，各层的细节信号依然存在冲击成分，但仍无法诊断故障位置。为进一步确认故障具体信息，需要提取滚动轴承各个部位的故障特征频率，选取db4 做Hilbert 包络并进行谱分析，结果如图5 所示。

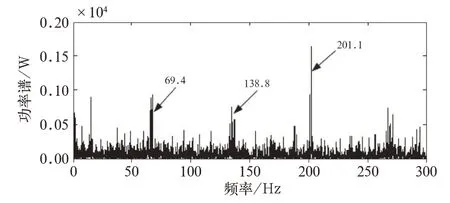
图5 I 号滚动轴承细节信号的包络图谱

由图5 可以看出，I 号轴承细节信号的尖峰频率为69.4、138.8、201.1 Hz 处，与外圈故障的特征频 率70.8 Hz、2 倍 频141.6 Hz、3 倍 频212.4 Hz 的理论计算值相对接近，结论与事实一致［1］。同时可以看到，0~50 Hz 内也出现了尖峰值，这是因为运行不久的轴承，主要受轴旋转、外部振动等固有因素的影响使能量聚集在低频段，不可避免。

采取同样的手法对II 号滚动轴承进行处理，小波技术处理后的每层细节信号如图6 所示，不难发现，各层细节信号都有冲击成分，但依然无法获得故障发生的部位。为了获取故障特征频率，对图6中细节信号做Hilbert 包络并进行谱分析，最终结果如图7 所示［1］。

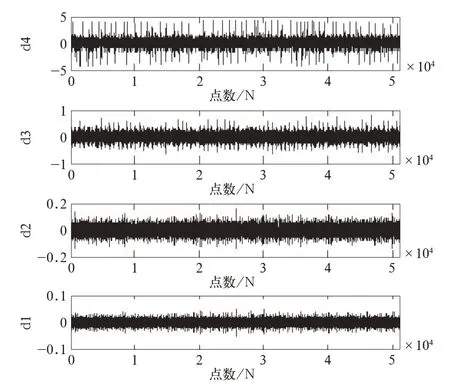
图6 II 号滚动轴承离散小波处理细节信号

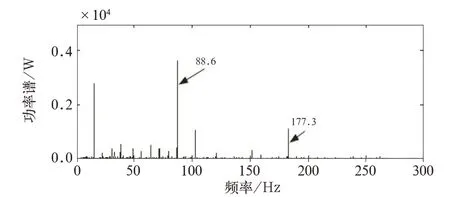
图7 II 号轴承细节信号的包络谱图

由图7 可以看出，在0~50 Hz 内出现了尖峰值，这是因为刚开始运行的轴承会受轴旋转、外部振源振动等固有因素的影响使能量聚集在此频段。关键是各层细节信号在88.6、177.3 Hz 处都呈现出显著的峰值，与滚动轴承内圈故障特征频率90.3 Hz、2 倍 频180.6 Hz 的 理 论 值 相 对 接 近，所以，可以诊断此滚动轴承的内圈发生了故障，结论与事实相符［1］。

4 结 论

通过对轴承故障数据解析，峭度指标对初期冲击类轴承振动信号十分敏感，适用于判断滚动轴承早期表面损伤类故障。在轴承故障检测中，峭度值K作为加速度的参考量，其取值仅代表故障变化的快慢程度，并不能反应故障的大小，只能粗略对轴承整体状态做判断。

小波分析利用不同的尺度将振动信号划分到不同的频带之内，消除噪音干扰的同时加强振动信号中故障成分的表现，同时，其在处理振动信号低频成分时能够具备较好的频率分辨率，处理振动信号高频成分时也具备较好的时间分辨率，解决了短时傅里叶变换中时间窗口恒定不变的问题，但它不能确定初期微弱信号的故障特征频率，也不能诊断出轴承故障的具体部位。采用Hilbert包络变换对小波包分解得到的细节信号做进一步包络谱分析，然后将图中尖峰值频率与计算出的故障特征频率做对比，进一步确认故障部位。

试验证明，将峭度值、小波分析和Hilbert 包络谱分析3 者结合用于滚动轴承的故障诊断中，可以有效提取出故障特征频率并诊断出故障位置，解决了傅里叶变换不能有效处理非平稳信号难题，取得了较好的效果。