轨道交通槽形梁桥静动力特性研究综述及展望

2023-11-10吴天群张智凯朱华中杨贤亮刘全民

铁道标准设计 2023年11期

吴天群，张智凯，朱华中，杨贤亮，刘全民

(1.南昌铁路勘测设计院有限责任公司,南昌 330002; 2.华东交通大学土木建筑学院,南昌 330013;3.中国铁路南昌局集团有限公司,南昌 330000; 4.江西地方铁路开发有限公司,南昌 330001)

引言

槽形梁是由道床板、边梁组成的一种下承式开口薄壁结构,与其他桥梁相比,槽形梁的边梁既可作为主要受力构件,又可抑制轮轨噪声的传播、防止车辆倾覆[1],同时能显著降低结构的建筑高度,在线路高程和桥下净空受限的情况下,槽形梁具有很强的竞争力。

槽形梁最早应用于1952年英国建造的罗什尔汉铁路桥梁,在此之后,槽形梁得以在国外的铁路桥梁和轨道交通桥梁中推广应用。巴黎地铁13号线的塞纳河路段采用了预应力槽形梁,法国里尔、智利圣地亚哥和荷兰鹿特丹的一些高架地铁段也均为预应力槽形梁,印度新德里地铁3号线近20 km的高架路段也成功使用了槽形梁形式,日本也已经形成了相应的槽形梁设计标准。

随着我国槽形梁设计理论和施工技术水平的提高,1995年我国第一座单线铁路连续槽形梁桥——葛水河铁路桥(图1)的建成,标志着槽形梁的工程应用得到进一步发展。

图1 葛水河铁路桥

在之后的广梅汕铁路畲汕段、天津京山特大桥先后采用了预应力混凝土铁路槽形梁[2],京沈高铁饶阳河特大桥以及板石山2号桥均成功应用了双线简支槽形梁,且运营多年状况良好。随后在我国城市轨道交通中也陆续使用槽形梁桥,预制预应力混凝土单线槽形梁,又称U形梁,第一次在广州地铁2号线得到应用,继而在上海、南京、重庆等城市轨道交通高架线(表1)中得到推广应用[3-4]。

表1 轨道交通高架线中槽形梁的应用

可以看出,国内外对于槽形梁的施工建造技术已经基本完善,槽形梁在铁路和城市交通中得到了长足的发展。但与箱梁相比,槽形梁的抗扭刚度和横向抗弯刚度较弱、中性轴偏低、边梁和道床板结合部位存在应力集中等问题,仍然是影响槽形梁结构安全的重要原因。

1 轨道交通槽形梁桥截面形式

槽形梁主要由边梁和道床板构成,边梁截面形式主要有I形、Γ形(直墙式或斜墙式)、箱形(图2)以及城市轨道交通U形截面,对于道床板一般有板式和箱形截面[5]。各截面形式及特点见表2。

表2 各截面形式特点

图2 槽形梁截面主要形式

在槽形梁的工程应用中发现,直墙式边梁和道床板连接处受力较为复杂,容易产生应力集中现象,从而导致混凝土开裂。采用斜墙式边梁可改善连接处受力,但会导致槽形梁顶部过宽,增大工程量。箱形截面边梁在边梁处设置横隔板,不仅可以改善结构受力,同时还可以在箱内锚固预应力筋,有着较好的外观效果。

当前铁路槽形梁根据线路的类型可以分为双线铁路槽形梁和单线铁路槽形梁。图3(a)所示为双线铁路槽形梁,相比单线铁路槽形梁,其横向较宽,横向抗弯刚度较弱,桥梁结构中心线与线路中心线不在同一位置,当列车单线通行时由于偏心荷载引起的扭矩对槽形梁受力不利。工程中多采用加大道床板厚度和全跨布置横向预应力筋的方式,但道床板的加厚不仅会使得结构自重增大,还会降低槽形梁截面的中性轴,增大了预应力损失,而且横纵预应力束交叉布置,施工工艺要求较高。之后有人提出关于双线槽形梁新的设计方案,在端支座处的道床板下设置横梁来改善受力,如图3(b)所示,只在横梁中布置横向预应力束,其他位置道床板厚度相应减小,如上海轨道交通6号线就成功采用这种结构形式。图3(c)为葛水河单线铁路槽形梁桥,单线铁路槽形梁其桥梁中心线和线路中心线重合,可以有效避免由于偏心荷载引起的扭矩。

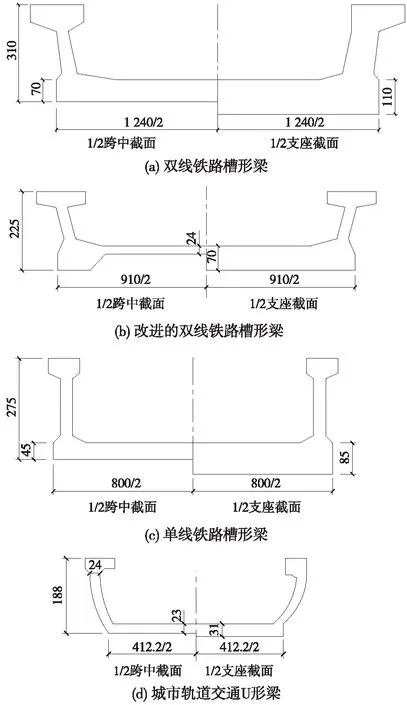
图3 不同线路槽形梁截面(单位:cm)

城市轨道交通U形梁,如图3(d)所示,道床板厚度比单线和双线铁路槽形梁的要小,道床板跨度只有双线的一半,采用U形截面形式,优化了槽形梁截面内受力情况,很大程度减少了槽形梁的横向弯矩,取消了道床板中横向预应力筋,降低了道床板厚度,极大地减小了槽形梁的自重,上海轨道交通8号线、16号线及南京轨道交通2号线等高架段均采用了这种结构形式。

还有学者针对槽形梁混凝土易开裂问题提出槽形钢-混凝土组合梁[6-7]、波纹钢腹板组合槽形梁[8-10]等结构形式,采用波纹钢腹板能有效解决腹板受剪而发生屈曲的问题,还可以减轻槽形梁自重,但是用钢量相对较大,应用有限。针对槽形梁桥的静力和动力特性,拟从计算模型研究、力学性能研究、温度梯度研究以及振动噪声研究4个方面回顾槽形梁国内外研究现状。

2 轨道交通槽形梁桥计算模型

当前轨道交通桥梁结构趋于大型化,体系趋于复杂化,在对其进行分析时,为便于设计人员能直接按照简单梁理论进行计算,建立简化计算模型,因而提出有效宽度的概念。通常将一定宽度的道床板视为边梁翼缘,与边梁组成计算截面,用材料力学的方法进行简化计算,使按照简化求得的边梁应力及挠度与实际桥梁一致,这个宽度就称之为有效宽度,假设道床板的应力分布在有效宽度内完全相同,如图4所示。其中2be为道床板有效宽度,2b为道床板宽度,阴影部分为组成的计算截面。需要注意的是,有效宽度的取值要使简化计算和理论计算得到的边梁应力分布基本一致,以便能真实地反映道床板中正应力分布的不均匀状况。

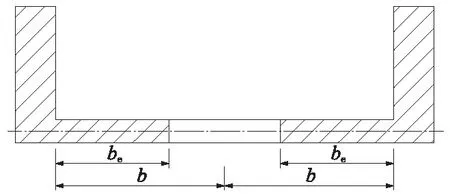
图4 有效宽度内道床板与边梁组成的计算截面

《铁路桥涵混凝土结构设计规范》[11]中关于箱梁有效宽度的规定是折减系数乘以板的宽度,折减系数主要取决于桥梁的宽跨比。而对于槽形梁的有效宽度,江新元和胡匡璋[12]提出规范中T形截面梁有效宽度的规定对于槽形梁也基本适用;周坚和涂令康[13]推导了道床板有效宽度的计算公式,并给出了供设计人员参考的有效宽度折减系数的图表;陆光闾[14-15]运用能量法提出道床板作为边梁翼缘作用的有效宽度公式,并结合连续槽形梁桥的空间作用分析给出了不同截面处有效宽度折减系数值。

当前槽形梁桥的空间分析法主要有解析法和有限元法。一般来说,当桥梁形状规整和边界条件比较简单时,运用解析法[16-17]可以快速分析桥梁受力状态,而对于工程中的变截面桥梁结构,难以根据实际情况来构建相应的桥梁简化模型。因此,一般采用有限元法并建立有限元模型的方式[18-19]进行桥梁空间分析。

槽形梁结构受力有着显著的空间特性,杆系计算模型很难准确分析槽形梁结构的真实应力状态,因此大多数槽形梁结构分析采用空间板壳计算模型和三维实体有限元模型。司万胜[20]分析了3种计算模型在铁路槽形梁计算中的应用,指出平面杆系计算模型在分析槽形梁受力状态时有很大不足,相比之下空间板壳模型可以准确分析槽形梁在弯扭共同作用下的力学特性;而对于三维实体有限元模型,不仅可以准确反映槽形梁的局部应力情况,还可以分析边梁和道床板结合部的复杂应力情况。

基于此,其他学者多使用实体有限元模型进行槽形梁应力和内力的研究。欧阳辉来[21]通过ANSYS中的实体单元建立槽形梁三维模型,分析槽形梁在传力锚固、恒载以及运营阶段的应力和变形,得出槽形梁结构在竖向荷载作用下会发生横向变形,其中边梁上翼缘内倾,相反下缘发生外斜的变形,使得边梁上下翼缘应力呈现出不同的变化规律。张文格等[22]通过建立三维实体有限元模型,得出运梁过程中的不平衡支撑基本不影响槽形梁跨中截面的横向变形,但对于跨中区域混凝土横向应力和其抗剪性能的影响较大。

3 轨道交通槽形梁桥力学性能研究

槽形梁是一种复杂的空间板梁组合结构,同时又属于开口薄壁构件,相比上承式结构,其抗扭性能较差、空间受力和变形复杂、构造要求高。因此,需要研究槽形梁的力学性能来保障槽形梁在施工和运营中的安全性和耐久性。国内外学者从应力分布、剪力滞效应、截面设计参数等方面研究了槽形梁的力学性能。

3.1 道床板横向计算

对于一般的轨道交通梁式桥,混凝土桥面板与主梁共同受力,在横桥向,结构自重、二期荷载、列车活载等会产生横向内力。对于桥面板横向内力计算,一般采用简支梁与连续梁模型。

槽形梁为下承式结构,道床板是槽形梁设计的关键要素之一。与上承式桥梁相比,下承式道床板代替了传统的桥面板结构,道床板横向受力的计算跨度增大,导致腹板对道床板的约束作用减弱。同时,槽形梁道床板竖向刚度相对边梁的竖向刚度较小,列车活载直接作用在道床板,再横向传递给两侧的边梁。由此可见,槽形梁的横向受力较为关键,在设计时应充分考虑,防止混凝土由于横向应力过大开裂。

李学斌等[23]通过梁体底板横向静载试验得出跨中和梁端均在底板下缘线路中心线偏外侧腹板处出现最大横向拉应变。江新元和胡匡璋[12]通过分析单线和双线试验桥中道床板的横向弯矩影响线,认为道床板最大横向弯矩值应该综合考虑恒载以及最不利活载的组合,并且给出了常规计算时的桥中心线和板端的横向弯矩系数。马坤全等[24]使用有限元分析小半径曲线段铁路槽形梁横向受力情况,得出在活载作用下跨中道床板顶面横向受压,底面横向受拉,且桥梁中心线横向应力远大于板边。何涛[25]在进行分片式槽形梁设计时,通过三维实体模型分析得出底板最大横向拉应力,进行钢筋混凝土配筋设计。张文格等[22]分析了在运梁过程中槽形梁的横向受力情况,角隅处横向应力偏大,受力最大位置在道床板下表面。

3.2 应力分布研究

在荷载作用下,槽形梁受力的空间特征表现为:边梁不仅发生竖向弯曲变形,而且会发生槽口处横向变形。边梁横向位移随着荷载增大而增大,此时槽口逐渐减小,即两侧边梁朝着相对的方向移动。由于弯曲和扭转的共同作用,导致槽形梁边梁的上缘部分应力分布出现不均匀现象;道床板则受纵向弯矩和横向弯矩共同作用,产生双向弯曲;边梁和道床板结合处往往受弯扭共同作用,容易出现应力集中现象[26]。

为提高梁端道床板的承载能力,往往在槽形梁端支座道床板处增加端横梁,该方法在一定程度上减小了端支座处道床板的横向应力,但对跨中道床板的作用并不显著[27-28]。陈波和赵晓波[29]采用施加初应变的方式来模拟预应力筋张拉,得出横向预应力筋的布置使得作用在道床板上的荷载向两侧边梁传递,而横纵预应力筋交叉布置,有效避免了道床板与边梁结合处的应力集中现象。

3.3 剪力滞效应研究

槽形梁边梁位于道床板两侧,荷载作用下的剪力流在由边梁向道床板横向传递的过程中,由于剪切变形会使剪力流出现滞后现象,导致正应力在道床板边缘处最大,桥梁中心线位置处最小。考虑剪力滞效应可真实地反映槽形梁的应力和位移分布情况,而忽略剪力滞的影响会使得槽形梁的实际应力大于设计应力,影响桥梁安全。因此,在槽形梁桥的设计计算和理论分析中,必须要充分考虑剪力滞效应的影响。

桥梁的剪力滞问题一般采用能量法[14,30]、势能原理、余能原理[13]来求解。但对于槽形梁,在进行剪力滞效应计算时,不仅要避免在设计时众多因素的影响,还要避免人为假设和简化模型带来的计算误差,所以采用解析解的方法来计算剪力滞效应有一定困难,而有限元和计算机技术的发展,使得更多学者使用有限元软件来分析槽形梁的剪力滞问题。有限元分析中一般使用剪力滞系数表示槽形梁的剪力滞效应,剪力滞系数=考虑剪切变形最大正应力值/按照初等梁理论计算得出的正应力值。

段敬民和钱永久[31]考虑剪切变形和剪切滞后翘曲应力的自平衡条件,提出了精确分析槽形梁静态和力学性能的方法。韦成龙和李斌[32]基于最小势能原理提出有限段法,可以分析变截面槽形梁剪切和剪力滞的双重影响。HU等[33]对简支梁桥的受力性能进行了理论研究,通过有限元分析验证了理论解的准确性,得出槽形梁整体弯曲和桥面板局部弯曲是引起槽形梁变形和应力的两个主要因素,同时由于剪力滞后效应,槽形梁的最大挠度可以放大到1.0～1.2倍。王淼和顾萍[34]为计算施工阶段和正常使用阶段槽形梁的力学特性,采用SAP90建立了槽形梁实体有限元模型,最终得出道床板的有效宽度和剪滞系数。卫星等[35]采用有限元法分析了W形连续槽形梁在顶推过程中的剪力滞效应。孙大斌[36]通过建立连续槽形梁的实体单元模型进行剪力滞效应分析,并计算出槽形梁的边支座截面、中支座截面和主跨跨中截面剪力滞系数分别为1.29、1.30、1.14,所求结果均比箱形截面的规范值要大。

3.4 截面设计参数研究

槽形梁边梁和道床板设计参数是影响槽形梁力学性能的关键因素之一,因此也有学者在这方面进行了分析研究。梁高增加会增大边梁的截面抗弯刚度,增大边梁承受纵向弯矩的能力,减小跨中截面道床板纵向拉应力、竖向位移[37]。同时,道床板厚度对槽形梁力学特性的影响也不容忽视,随着道床板厚度增加会使槽形梁的纵向压应力和竖向位移减小,相反会增大截面的横向应力[38]。可以看出,相比道床板厚度增加,边梁高度对力学性能的改变更为重要,但梁高受建筑高度和建造成本的限制,还需要结合实际工程情况确定。

4 轨道交通槽形梁桥温度梯度

桥梁结构中混凝土材料导热性能差,在日照、风速等外界环境影响下,混凝土桥梁温度场呈非线性分布,而其产生的温度应力和变形会使得桥梁结构出现开裂情况,影响桥梁结构安全、耐久性[39-41]。桥梁截面形式以及日照时间和日照强度、风速等是造成桥梁温度场发生变化的重要因素。在日照辐射较强的地区,太阳照射下桥梁产生的温度应力甚至可能会超过活载应力,因此针对桥梁温度梯度的研究就显得极为重要。

薛嵩等[42-43]建立了考虑大气环境参数、桥梁方位走向、梁体遮挡作用的槽形梁斜拉桥热力学分析模型,得出边梁高度、混凝土表面辐射吸收率、大气透明度系数等参数对槽形梁的竖向温差模式影响不大;又以应力等效为原则,拟合出如图5所示的槽形梁箱室温差模式,槽形梁边梁上缘最大温差为20 ℃,边梁腹板内温差符合指数函数分布,而在边梁下缘,最大温差为2.5 ℃,在0.2 m范围内线性变化至0 ℃。董旭等[44]结合实际监测与有限元模型,得出U形梁的横向温度梯度在朝阳侧腹板中部较为明显,而在其他部位较小;对于竖向温度梯度,在腹板处为分段函数,在道床板处为指数函数。梁岩等[45]通过建立实体有限元模型,发现槽形梁的竖向温度不呈线性变化,图6所示为结构所施加的第1种温度梯工况,槽形梁的横纵应力和竖向位移都会受到竖向温度梯度的影响,系统温差增大会导致槽形梁的横向纵向位移增大。

图5 槽形梁箱室的温差模式[42](单位:cm)

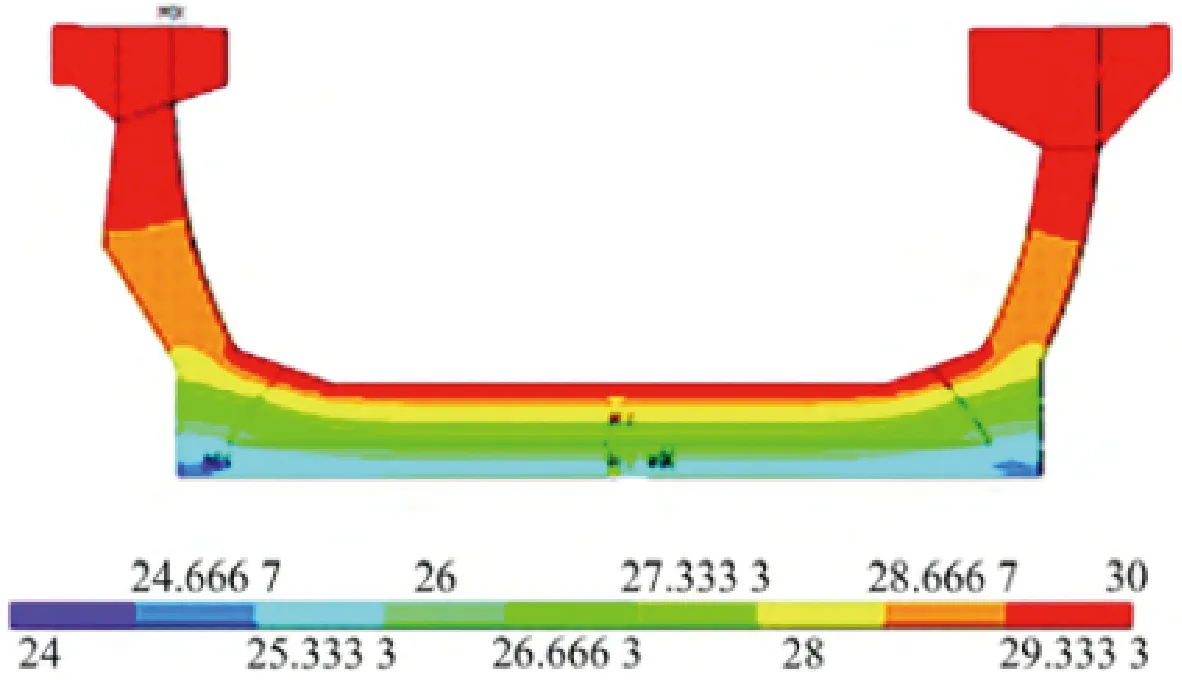
图6 竖向温度梯度下的温度分布示意[45](单位:℃)

对于桥梁的温度梯度模式,国内外研究和规范多针对于普通T梁和箱梁。槽形梁不同于上述桥梁,属于开口薄壁结构,本身受太阳辐射面积大,其温度梯度分布模式有很大不同。因此,对于槽形梁的温度梯度情况还需要进一步分析确定,以期能形成温度梯度模式标准。

5 轨道交通槽形梁桥振动与噪声研究

轨道交通槽形梁结构虽然可以有效减少轮轨噪声等传播,但对于桥梁本身结构噪声问题却没有得到很好的解决。桥梁结构噪声主要是以低频为主,具有较强的穿透力和传播力,危害着桥梁附近居民的身心健康。因此,对槽形梁结构噪声进行理论研究,同时探究减振降噪的相关措施有着重要意义。

目前对于槽形梁振动研究多采用车桥耦合模型,曾峰等[46]基于ANSYS和SIMPACK软件形成如图7所示的桥梁模型和车辆模型计算系统,计算轮轨激振力,并加载到耦合模型中,最终得出轨道交通槽形梁结构的振动响应。

图7 车桥耦合模型[46]

针对槽形梁的减振降噪研究,刘林芽等[47]研究发现,槽形梁腹板横向、道床板垂向振动加速度以及槽形梁结构噪声的峰值频率均在63 Hz左右;同时分析腹板、道床板以及翼缘板厚度和腹板半径等因素对槽形梁结构噪声的影响,认为腹板厚度增大会使远场点的噪声有一定程度减小;翼缘板厚度对槽形梁结构噪声的影响较小,而道床板厚度增加,可以减少桥梁附近结构噪声,相反对远场点的结构噪声影响甚微[48]。

韩江龙等[49]也得出增加道床板厚度相比增加腹板厚度的降噪效果要好,槽形梁翼缘板的横向振动响应最大,最大振动加速度级为107.2 dB。宋晓东和李奇[50-51]为对比声屏障、高弹性扣件和梯形轨枕3种措施的减振降噪效果,采用车-轨-桥模型以及声学有限元/无限元方法,得出声屏障可以有效控制钢轨噪声,而高弹性扣件和梯形轨枕可以有效降低U形梁结构噪声。李克冰等[52]采用车桥耦合动力理论和间接边界元法,对比槽形梁各构件的声压贡献系数,得到了如图8所示的声压贡献系数等值线图,证明了地面附近的噪声基本由道床板产生。