高速铁路大跨度钢桁架-混凝土板组合梁斜拉桥稳定性研究

2023-11-10刘振标夏正春胡方杰余万庆

铁道标准设计 2023年11期

刘振标，夏正春，胡方杰，余万庆，施洲

(1.中铁第四勘察设计院集团有限公司桥梁设计研究院,武汉 430063; 2.西南交通大学土木工程学院,成都 610031)

引言

近年来,我国高速铁路桥梁建设发展迅速,新型桥梁结构形式不断发展。其中,钢桁架-混凝土板组合梁斜拉桥因其自重轻、跨越能力大、经济性好且能够充分发挥钢材和混凝土两种材料的力学性能而颇受设计者们的青睐[1-3]。在铁路钢桁架-混凝土板组合梁斜拉桥受力中,主梁钢桁架在自重、列车荷载以及斜拉索力作用下整体压弯受力,部分钢桁架杆件为受压状态,其整体及部分杆件的稳定性问题值得关注。

桥梁稳定问题由来已久,也有大量研究成果[4-7]。理想线弹性稳定分析结果能够提供一定的参考,但由于忽略了结构在制造、安装等带来的施工误差以及材料非线性因素影响,导致高估了结构的稳定性[8-9]。随着稳定理论及有限元计算的发展,非线性因素对稳定影响能够予以准确考虑,并应用于复杂桥梁结构的稳定性分析。施洲等[10]依托双主跨2×360 m下承式钢桁架拱桥开展考虑几何初始偏位、几何和材料双重非线性因素影响的稳定性分析,分析结果表明,在运营阶段各荷载组合下结构的最小稳定系数为10.152,考虑最大几何初始偏位以及双重非线性因素影响下结构最小稳定系数为2.392,均满足规范要求。赵曼等[11]采用有限元计算方法对跨度128 m新型铁路应急钢桁梁的稳定性进行研究,结果表明:横向风压在大于和小于0.6 kPa时,结构的失稳形式不同;不同方向的几何初始变形仅对该方向的失稳模态影响显著。吕梁等[12]依托南京长江五桥工程,分析几何与材料非线性因素影响下该桥的稳定系数,得到施工和运营阶段下结构最小非线性稳定系数分别为2.20和2.23,且均满足规范要求的结果。马明等[13]对新月型拱桥的极值点稳定问题进行了研究,结果表明,当提高混凝土强度等级或钢管混凝土的含钢率时,能够提高该桥的极限承载能力;考虑双重非线性因素影响后,对结构的稳定系数影响显著。闫纾梅[14]通过数值模拟与理论分析,对某钢桁梁斜拉桥开展稳定性分析,研究结果表明,该桥在施工期间的第一类和第二类稳定系数均满足要求,而该桥的失效路径是部分斜拉索的应力首先达到破断强度而退出工作,使得主桁受力增大,达到该桥的极限承载力。童小龙等[15]以钢筋混凝土受压构件为例,从可靠度指标方面入手分析了结构稳定系数的取值范围,并指出当第一类稳定系数为4.0时,并不能完全保证结构发生第二类失稳时的可靠指标达到目标可靠指标。既有文献也表明,是否考虑非线性影响因素对桥梁结构的稳定系数量值影响显著。

目前,既有桥梁稳定性研究主要集中在钢结构桥梁,涉及大跨度钢桁架-混凝土板组合梁斜拉桥的稳定性研究相对较少,而高速铁路大跨度钢桁架-混凝土板组合梁斜拉桥研究则更少。基于主跨300 m深茂铁路深江段虎跳门水道特大桥主桥斜拉桥,采用有限元软件ANSYS建立大桥空间杆系有限元模型,分析其在运营阶段不同荷载(恒载、列车活载、风荷载)作用下的稳定性,并探讨几何初始变形、几何非线性和几何及材料双重非线性因素对桥梁稳定性的影响规律。

1 钢桁架-混凝土板组合梁斜拉桥稳定性理论

铁路钢桁架-混凝土板组合梁斜拉桥在自重、列车荷载、斜拉索力作用下,主梁和桥塔承受巨大的轴力及一定的弯矩,对于钢桁架-混凝土板组合梁,除组合梁整体稳定外,其受压的弦杆、腹杆等构件还存在局部杆件稳定性问题。根据失稳的性质,铁路钢桁架-混凝土板组合梁斜拉桥的稳定问题可以分为两类[16-17]。第一类是理想线弹性稳定分析,但对于大跨度铁路钢桁架-混凝土板组合梁斜拉桥而言,考虑制造、运输、安装导致结构的几何初始变形以及材料非线性因素影响的稳定分析更为关键,即第二类稳定分析,其基本方程为

(KE(k)+KG(k)+K1(k))×U=P

(1)

式中,KE(k)为考虑初始几何偏差的桥梁结构的弹性刚度矩阵;KG(k)为考虑初始几何偏差的几何刚度矩阵;K1(k)为考虑初始几何偏差的大位移刚度矩阵;k为桥梁结构初始几何偏差参数;U为节点位移向量;P为节点荷载向量。

在进行考虑几何初始变形的第二类稳定分析时,可通过改变k的大小来考虑不同程度的几何初始变形。由于大位移刚度矩阵K1随着荷载增大而不断变化,使得式(1)的总体刚度矩阵也在不断变化,导致其求解也变得更为困难。文献指出[7,18],增量迭代法在求解非线性稳定问题时具有较好的效果,因此,在采用ANSYS进行第二类稳定分析时多采用增量迭代法,根据结构荷载-位移曲线中的突变点,求解得到桥梁稳定系数λ。

铁路钢桁架-混凝土板组合梁斜拉桥主梁的钢桁架正弯矩区上弦杆、负弯矩区下弦杆以及传递剪力较大梁段的腹杆[19]在自重及列车外荷载下承受显著的轴向压力,其在压力荷载下可能会发生失稳破坏。压弯构件在弯矩作用平面内的整体稳定计算公式为[20]

(2)

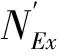
2 工程概况及有限元模型

2.1 工程概况

新建深茂铁路虎跳门水道特大桥主桥为设计时速250 km的上承式钢桁架-混凝土板组合梁斜拉桥,其跨径布置为(64+80+300+80+64) m,大桥结构形式如图1所示。大桥设计荷载为双线ZK荷载。大桥主梁由桁间距13 m的两片桁架及其上铺设Π形混凝土桥面板组成的高5.9 m钢桁架-混凝土板组合梁,混凝土桥面板与钢上弦杆通过PBL剪力键及剪力钉连接。混凝土桥面板在主梁中心线处高40～70 cm,在钢桁架上弦杆处高1.2 m。主桥钢桁架采用N形桁式,桁高4.3 m、节间长度4 m,每个节段长12 m,包括3个节间。中跨下层的钢弦杆之间采用X撑作为下平联,边跨下层的钢弦杆之间采用混凝土板作为桁架下平联,既能够增大主梁的纵、横向刚度,同时作为压重避免边跨主梁支座出现负反力。钢桁架上弦杆采用倒Π形截面,其上设置剪力钉与上层桥面板相连;主跨下弦杆为H形截面,边跨及次边跨为箱形截面,其中在边跨下弦杆内填充混凝土以形成PBL加劲型矩形钢管混凝土,提升主梁的承载能力、稳定性及刚度。主跨及边跨的主梁横截面如图2所示。全桥共设有48对斜拉索,斜拉索锚固于主梁上弦节点处,提升了桥面板的整体性。

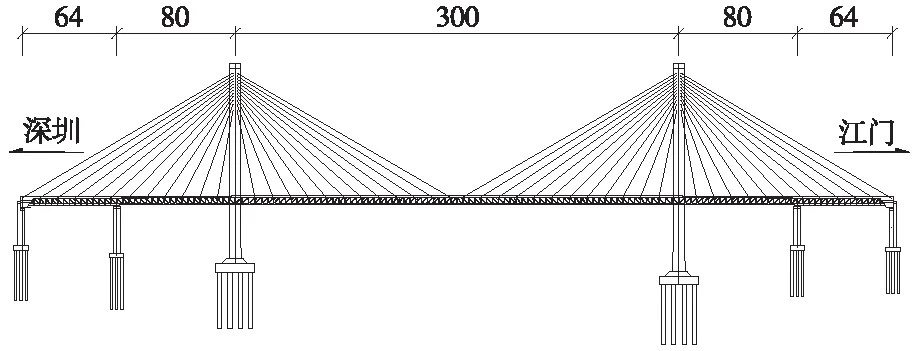
图1 主桥立面布置(单位:m)

图2 主梁横截面(单位:mm)

主梁钢结构均采用Q345qD钢材,剪力钉采用材料为ML15圆柱头焊钉。钢桁架-混凝土板组合梁斜拉桥桥面板预制部分采用C60高性能混凝土,为减小混凝土收缩徐变对主梁受力的影响,通过现浇C60补偿收缩钢纤维混凝土将预制桥面板与主梁连接。

虎跳门大桥主梁通过钢桁架加劲混凝土形成以混凝土桥面板受力为主的钢桁架-混凝土板组合梁,其梁高远小于常规钢桁架梁(14.0～16.0 m),与铁路钢箱梁的梁高(5.0 m左右)较为接近。与常规钢桁架梁相比,该桥型的稳定性问题尚缺少可以参考的文献资料,因此,该桥型的稳定性问题值得进一步研究,研究成果可以为后续同类桥型的稳定性研究提供参考。

2.2 有限元模型

针对高速铁路大跨度新型钢桁架-混凝土板组合梁斜拉桥,为探索其稳定性,依托虎跳门水道特大桥主桥工程,采用有限元软件ANSYS建立以空间梁单元为主的空间杆系有限元模型(图3),以分析其稳定性能。有限元模型中,除斜拉索采用空间杆单元(LINK8)模拟外,其余杆件均采用空间梁单元(BEAM188)模拟,混凝土桥面同样等效为空间梁单元。由于斜拉索锚固在钢上弦节点板处,因此,在建模时斜拉索与桥塔和钢上弦之间采用共用节点的方式进行连接。通过约束方程来模拟主梁与墩及桥塔之间约束,其中主梁与辅助墩及连接墩之间约束竖向、横向自由度,释放顺桥向的自由度;主梁与桥塔之间约束竖向及横桥向自由度,在顺桥向设置刚度为1 000 kN/m的弹簧单元来模拟黏滞阻尼器。全桥共计2 315个节点以及3 416个单元。

图3 有限元模型

在稳定性分析中,主要考虑桥梁在运营过程中所承受的荷载,包括恒载、列车活载以及风荷载。在ANSYS有限元模型中通过施加重力加速度模拟一期恒载,二期恒载和列车活载采用梁单元荷载模拟。其中,二期恒载设计值为171 kN/m,列车活载为双线ZK活载。

3 线弹性稳定分析

3.1 线弹性稳定分析

为了解大跨度铁路钢桁架-混凝土板组合梁斜拉桥在运营阶段的稳定性,采用有限元弹性屈曲分析求解其在4种不同列车荷载与恒载组合下的稳定系数及失稳模态。各荷载组合工况及相应工况下前5阶稳定系数如表1所示。

表1 前5阶线弹性稳定系数

由表1可以看出,运营阶段不同荷载组合下,结构稳定系数各不相同。其中,工况4(恒载+主跨双线列车活载+横风荷载)的一阶稳定系数最小,为7.639,大于规范要求的4.0,表明其具有良好的稳定性。工况2与工况1相比,考虑横风荷载后,结构的一阶稳定系数降低1.312,减小幅度为13.79%;工况4与工况3相比,考虑横风荷载后,结构的一阶稳定系数降低0.993,减小幅度为11.50%,表明横风荷载会降低桥梁结构整体稳定性。此外,4个工况下第二、三阶稳定系数和第四、五阶稳定系数分别相同,表明第二、三阶失稳模态和第四、五阶失稳模态为对称失稳模态。

以最不利工况为例,其前5阶失稳模态如图4所示。由图4可以看出,第一阶失稳模态形式为主梁整体纵飘及塔纵弯失稳;第二、三阶失稳形式和第四、五阶失稳模态形式分别相同,均为桥塔处主梁局部杆件横向失稳。

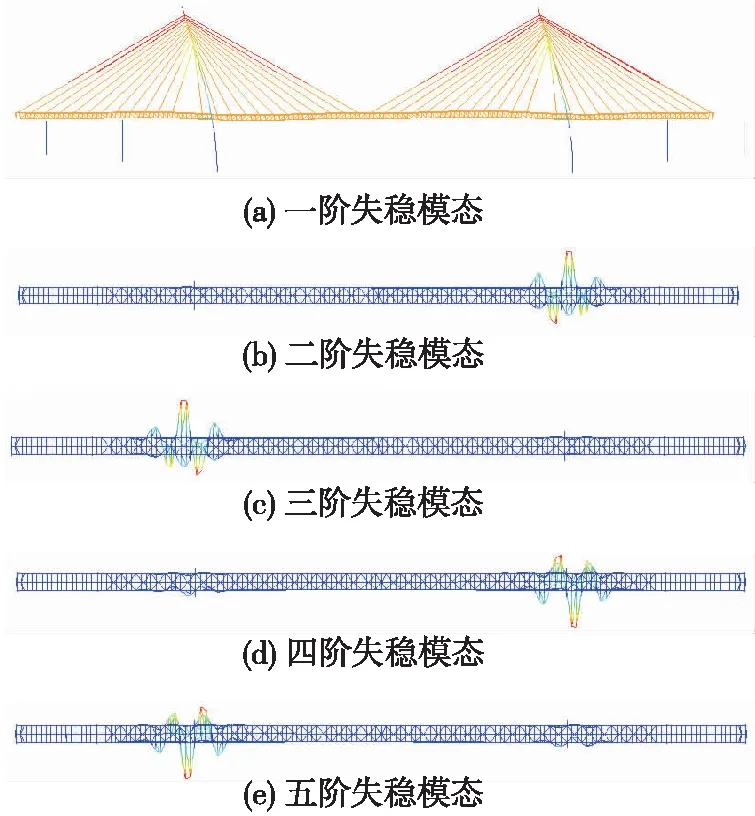
图4 工况4前5阶失稳模态

3.2 考虑几何初始变形影响的线弹性稳定分析

用于桥梁结构的材料(钢材、混凝土等)在制造加工、运输及安装等过程中,由于材料自身缺陷、技术人员失误等因素,会造成桥梁结构在运营前出现不同程度的缺陷。TB10091—2017《铁路桥梁钢结构设计规范》[21]规定,结构几何初始变形k不应超过L/1 000,其中L为计算跨径。为研究不同程度几何初始变形对铁路钢桁架-混凝土板组合梁斜拉桥稳定性的影响规律,选取k为L/3 000、L/2 000和L/1 000进行考虑几何初始变形的线弹性稳定分析。在ANSYS有限元模型中,几何初始变形分别考虑一、二、四阶代表性失稳模态变形结果来施加,并考察其对稳定性的影响[10]。各工况在考虑不同初始变形的线弹性稳定分析结果如表2所示。

表2 考虑几何初始变形影响的线弹性稳定系数

由表1和表2可知,考虑几何初始变形后,稳定系数均有不同程度的减小,其中在工况1下,结构一阶稳定系数由9.511降低至8.463,降低11.02%;在工况3下,结构一阶稳定系数由8.632降低至7.855,降低9.01%。此外,各工况下二阶和四阶线弹性稳定系数表现出与一阶稳定系数相似的变化规律,当考虑最大几何初始变形(k=L/1 000)后,最不利工况(工况4)的二阶和四阶稳定系数分别为7.293、8.060,满足规范要求。桥梁结构稳定系数与几何初始变形呈现负相关的变化规律,当几何初始变形增大时,结构稳定系数逐渐降低。考虑初始变形的影响后,仅使得结构的稳定系数有所减小,但结构的失稳形式未发生变化。以工况4为例,其前5阶失稳形式与未考虑初始变形的失稳形式完全一致。

4 非线性影响下稳定性分析

根据线弹性稳定分析结果,工况4(恒载+主跨双线列车荷载+横风荷载)为运营阶段下的最不利工况,故以工况4为基础,开展对铁路钢桁架-混凝土板组合梁斜拉桥的第二类稳定分析。在第二类稳定分析中几何初始变形仍取k=L/3 000、k=L/2 000和k=L/1 000,初始变形的施加方法与考虑初始变形的线弹性稳定分析施加方法相同。

4.1 几何非线性对桥梁稳定性影响

在桥梁结构的稳定性分析中,几何非线性(即P-Δ效应)的影响不容忽视。在ANSYS有限元模型分析中,考虑几何非线性的影响,可通过打开几何非线性开关(NLGEOM,ON)来实现。考虑几何非线性影响下不同几何初始变形结构在工况4下的稳定系数结果见表3。由表3可知,当仅考虑几何非线性时(即k=0),结构一阶稳定系数由7.639减小为6.781,相比于线弹性分析结果,稳定系数降低11.23%。当k=L/3 000时,一阶稳定系数减小5.09%;而当k=L/1 000时,一阶稳定系数减小至5.703,减小率达到15.90%。此外,结构二阶和四阶稳定系数与线弹性稳定系数相比均有不同程度的减小。当k=0时,结构二阶和四阶几何非线性稳定系数分别减小0.458、0.988,减小率分别达到5.44%、10.13%;几何非线性稳定分析下,考虑最大几何初始变形(k=L/1 000)后,二阶和四阶稳定系数分别降低13.84%、14.61%。由此可见,桥梁结构的稳定系数与几何初始变形呈现出负相关的变化规律。由于文中最大几何初始变形仅为L/1 000,当其继续增大时,结构的稳定系数减小幅度将会更大。

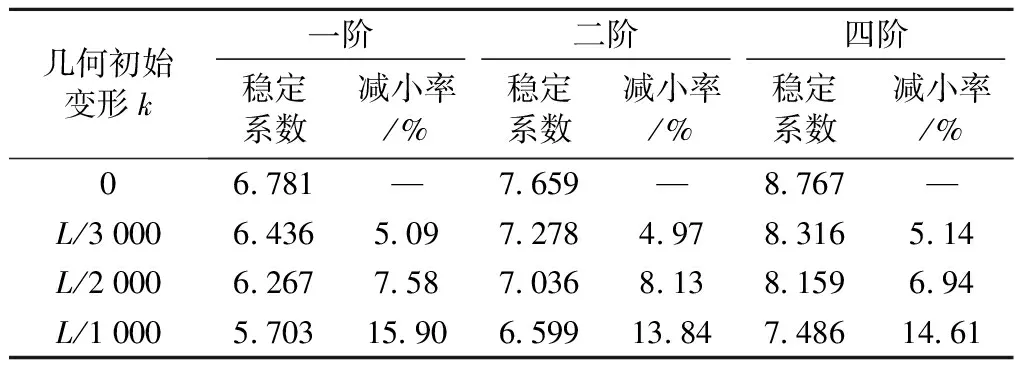
表3 不同几何初始变形下考虑几何非线性稳定系数结果

考虑几何非线性影响下,不同几何初始变形稳定分析中结构的荷载-跨中纵向位移曲线如图5所示。当荷载较小时,随着荷载逐渐增大,荷载-位移曲线呈线性增大;在跨中纵向位移达到2.0 m左右时,曲线斜率变小,纵向位移的增加速度逐渐加快,表明此时结构进入弹塑性状态;当跨中纵向位移达到3.2 m左右时,曲线斜率进一步减小,可认为此时结构已进入塑性状态,失去承载能力。其原因是当跨中纵向位移达到2.0 m左右时,位于桥塔处的下弦杆开始出现横向微小变形,随荷载增大,该变形不断发展,当跨中纵向位移达到3.2 m左右时,由于该下弦杆局部失稳导致结构失效。此外,当初始变形较小时,荷载-位移曲线近似重合,但随着几何初始变形增大,荷载位移曲线逐渐分离,但不同初始变形下荷载-位移曲线的变化规律相同。

图5 考虑几何非线性的一阶稳定系数与跨中纵向位移曲线

4.2 几何与材料双重非线性对稳定性影响

在ANSYS有限元模型中,考虑材料非线性的非线性稳定分析可以通过定义材料的应力-应变关系来实现,虎跳门大桥稳定性分析中,Q345qD钢材的应力-应变关系采用双线性随动强化模型BKIN来模拟,C60混凝土材料的应力-应变关系采用多线性随动强化模型MKIN模拟,如图6所示。考虑不同几何初始变形的双重非线性稳定系数见表4。

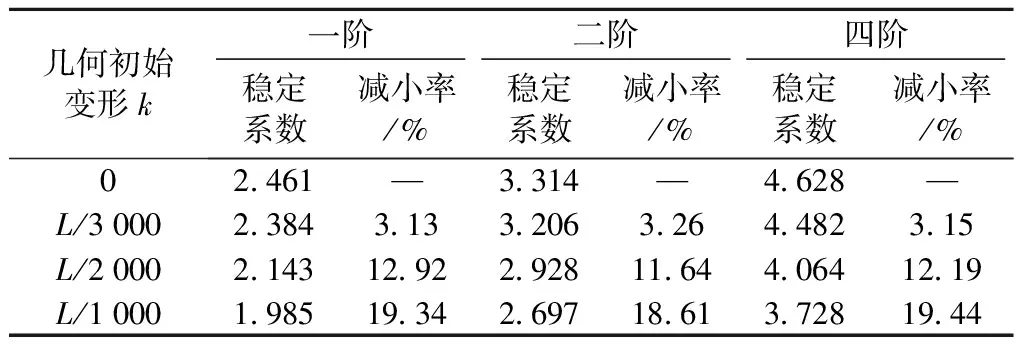
表4 不同几何初始变形下的双重非线性稳定分析结果

图6 材料应力-应变关系曲线

由表4可知,当仅考虑双重非线性影响时(k=0),结构稳定系数由7.639减小为2.461,相比于线弹性分析结果,稳定系数降低67.78%,与几何非线性分析相比,稳定系数降低63.71%;当k=L/3 000时,稳定系数减小3.13%,而当k=L/1 000时,稳定系数仅为1.985,减小率达到19.34%,此外,结构二阶和四阶稳定系数的减小率分别达到18.61%、19.44%。线弹性稳定分析得到的稳定系数明显大于考虑双重非线性稳定分析的结果,表明线弹性稳定分析会显著高估铁路钢桁架-混凝土板斜拉桥的整体稳定性。

考虑不同几何初始变形的双重非线性稳定分析下结构的荷载-纵向位移曲线如图7所示。由图7可见,考虑双重非线性影响的荷载-位移曲线与仅考虑几何非线性影响的曲线表现出相同的变化规律。在荷载较小时荷载-位移曲线为直线,当跨中纵向位移达到1.0 m时,荷载-位移曲线斜率减小,最终当跨中纵向位移达到1.3 m时,斜率进一步减小,此时结构失去承载能力。其原因仍为靠近桥塔处的下弦杆局部失稳而导致结构的整体失稳。当结构纵向位移达到1.0 m时,曲线斜率明显大于仅考虑几何非线性因素影响的曲线斜率,并且结构处于弹塑性状态的时间更短,进一步说明材料非线性对铁路钢桁架-混凝土板组合梁斜拉桥的稳定性影响更大。

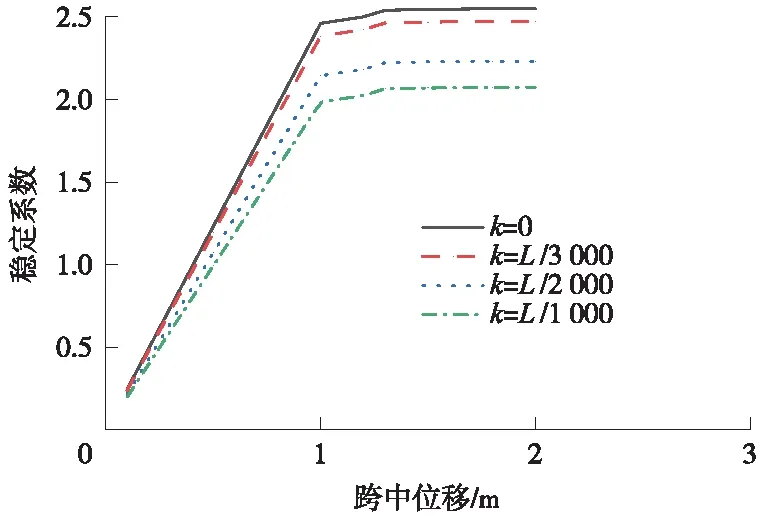
图7 考虑几何及材料非线性的稳定系数与跨中纵向位移曲线

4.3 不同类型稳定系数对比分析

铁路钢桁架-混凝土板组合梁斜拉桥在工况4荷载作用下,线弹性稳定分析与非线性稳定分析的稳定系数见表5。由表5可知,在k=L/1 000时一阶线弹性稳定系数与几何非线性稳定系数差值最大为1.448,k=L/2 000时与双重非线性稳定系数最大差值为5.489,降低幅度分别达到20.25%、71.92%,表明材料非线性对该桥稳定性的影响程度远大于几何非线性,在考虑几何初始变形以及非线性因素的影响后才能够准确地评估铁路钢桁架-混凝土板组合梁斜拉桥的整体稳定性。当考虑L/1 000的几何初始变形后,一阶线弹性稳定系数、几何非线性稳定系数和双重非线性稳定系数分别减小0.488、1.078和0.476,降低幅度分别达到6.39%、15.90%和19.34%,表明几何初始变形对铁路钢桁架-混凝土板组合梁斜拉桥稳定性的影响在20%以内。同时考虑最大几何初始变形(k=L/1 000)、几何非线性和材料非线性因素的影响时,铁路钢桁架-混凝土板组合梁斜拉桥的一阶稳定系数仅为1.985,TB 10095—2020《铁路斜拉桥设计规范》[22]中规定,钢斜拉桥的第二类稳定系数应不小于1.7,表明铁路钢桁架-混凝土板组合梁斜拉桥整体稳定性良好,能够满足结构的使用需求。此外,结构二阶和四阶稳定系数表现出与一阶稳定系数相似的变化规律,考虑最大几何初始变形和非线性的影响,稳定系数分别为2.697、3.782,进一步表明铁路桁架-混凝土组合梁斜拉桥的稳定性良好。