一道2022年江西预赛试题的多解探究与变式
2023-11-10徐凤旺尹正波
中学数学研究(江西) 2023年11期
成 敏 徐凤旺 尹正波
贵州师范大学数学科学学院 (550025)
1 试题呈现
分析:这是2022年全国高中数学联赛江西赛区的一道根式函数求最大值的试题.文[1]通过三种方法求得该函数的最大值,并对其试题进行了相应的变式,读后深受启发,于是对该题做进一步的探究,得到了不同于文[1]中的三种解法和试题的几个变式,与大家一起分享.
2 试题解析



评注:此解法通过换元法,构造二次函数,将问题转化为二次函数的Δ≤0,即可求得该函数的最大值.
解法3:(构造随机变量X的分布列)由题意可得,可构造随机变量X的分布列为:

Xxy+5yz+5zx+5P131313
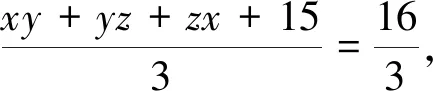
评注:此解法通过构造随机变量X的分布列,结合(EX)2≤EX2,求得函数的最大值.
3 试题变式

3.1 三元形式的变式





评注:此变式是将不等式每一项根号下未知数的幂从“1”变为“2”得到.


评注:此变式是将不等式每一项根号下的未知数的系数和常数项改变得到.


评注:此变式是通过改变不等式每一项的幂得到.


评注:此变式是通过改变不等式每一项根号下的代数式的结构得到,将每一项根号下未知数的个数从“1”元变为“2”元.


评注:此变式是通过改变不等式每一项根号下的未知数的幂和系数得到.
3.2 四元形式的变式




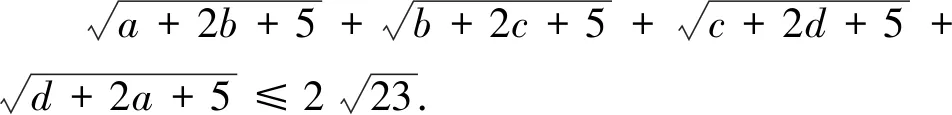

上述变式7到变式12均是在变式1到变式6的基础上改变的,将未知数的个数从“3”元变到“4”元,变式7到变式12的证明方法分别对应变式1到变式6的证明方法,证明方法一致,此处不再叙述.
