一道椭圆模拟题的解法与结论推广
2023-11-10湛怀玉
湛怀玉
湖南省长沙市南雅中学 (410027)
1 试题呈现


图1
该试题考查圆锥曲线的综合应用,涉及的主要考点有:椭圆几何性质的应用,直线与椭圆位置关系及求最值等.第(1)小题,由于求的是角的余弦值,因而与三角函数、三角恒等变换知识或与向量运算紧密结合,体现知识间的相互渗透应用;第(2)小题,求两线段长度之积的最大值,设出直线的斜率,以此为参数,表示出长度之积,利用函数或均值不等式求最值.
2 试题解析
首先看第(1)小题的解法.


点评:解法1根据直线MN与直线AC平行,转化为斜率相等,然后转化为角的关系.再利用斜率的定义,得到角的三角函数,最后利用三角函数的诱导公式和二倍角公式求解的.

点评:解法2联立直线与椭圆方程分别求得点M、P的坐标后,转化为向量坐标,然后利用两向量夹角坐标公式求得数量积,较为简捷.
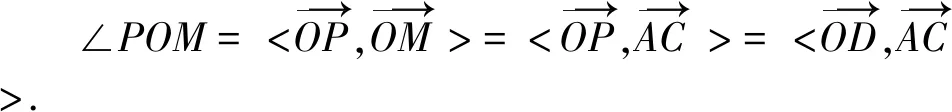
点评:解法3根据直线MN与直线AC平行,转化为两向量夹角相等,然后利用两向量夹角坐标公式求得数量积,充分展现了向量求解夹角问题的优越性.
下面再来看第(2)小题的解法.


下面采用三种解法求解PQ·MN的最大值.

点评:解法1整体设参后将表示为关于参数倒数的二次函数,分离、配方利用二次函数的最值知识求解.

点评:解法2整体设参后将OM2·OP2表示为关于参数倒数的函数,求导、利用导数研究函数的单调性知识求解,体现了导数的工具作用.

点评:解法3首先求得OM2+OP2=5(定值)后,利用重要不等式求得最值.相比而言,解法3是一种最为简捷的方法,但要注意具备定值和等号成立的条件.
3 结论推广
在上面解答试题的过程中,我们可以看到,直线MN与PQ的斜率之积为定值,那么对于一般情形的椭圆是否有同样的结论?经探究,于是我们得到下列结论1.

证明:以A是椭圆长轴的左端点(左顶点),且点P、C、M在x轴的上方为例来证明.
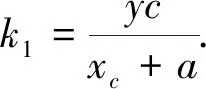
试题第(2)小题是求具体椭圆中PQ·MN的最大值,那么,能否将第(2)推广为一般情形?经探究,于是我们得到下列结论2.

证明:以A是椭圆长轴的左端点(左顶点),且点P、C、M在x轴的上方为例来证明.

