一道测试题的求解、溯源与拓展
2023-11-10张志刚
张志刚
山东省宁阳县复圣中学 (271400)
一、试题呈现
A.8 B.10 C.9 D.其他三个答案都不对
本题在无显性方程条件下,探求二元三角函数的最值问题,考查数学运算、逻辑推理、数学抽象等核心素养,试题设计简洁清新,思维跨度较大,颇具综合性、挑战性和选拔性.
二、试题解答
思路一 分步消元








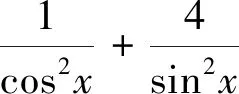
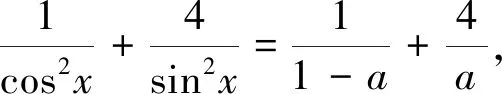
点评:通过本解法,我们可进一步体会导数讨论函数(含高次多项式函数、分式函数、三角函数、数列等)单调性的普适性,体会知识之间的有机衔接与融合.


点评:“二次方程有解则判别式大于等于0”是学生最早接触、最为熟悉、最易掌握的方法.美中不足的是,上述解答在得到方程ma2-(m+3)a+4=0后,需对二次项系数分类讨论,如何规避分类讨论简化问题呢?由于“三个二次”紧密相联,可转而讨论相应不等式恒成立问题.
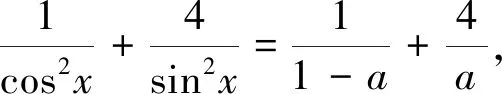

思路二 直接消元

点评:本解法借助常数“1”的两次代换及柯西不等式工具求出最小值,需要考生具备较强的观察能力和代数变形能力.
思路三 高等数学观点
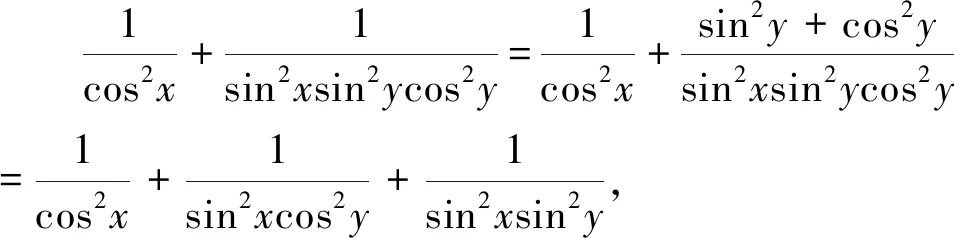
点评:尽管在理论上偏导数法是便捷的,但在实际解题过程中,中学生却面临不小的挑战.例如,学生理解偏导数法的原理需要较长的过程,求偏导运算对于学生而言也是陌生的,求解方程组需要较强的运算求解能力,等等,在此仅供读者参考.
除了上述思路,本题作为选择题,自然也可考虑代入验证法,当然从逻辑上是不严谨的,也非真实的命题意图.
三、试题探源

二者函数解析式的构造方式和解法基本一致,下面运用不等式放缩解答上题,其他解法不再赘述.

A.18 B.16 C.8 D.6

四、试题拓展
1.互换变量

由于本题中变量x,y的地位相同,故交换二者的位置不影响结果.
2.置换函数

参照以上解法解答,可知变换两个三角函数的名称不影响结果.
3.常值推广

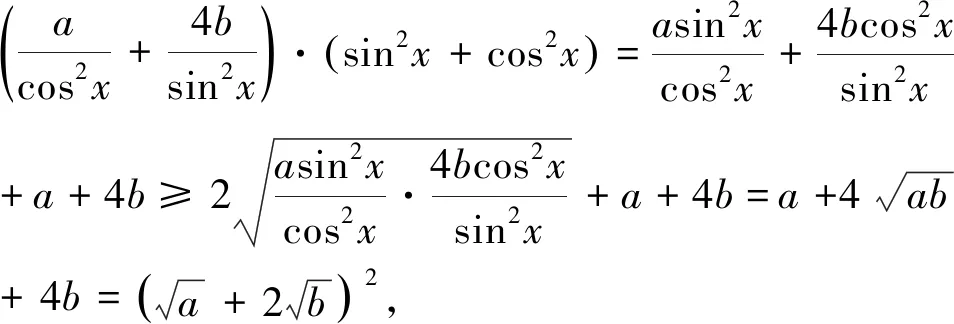
五、类题训练
1.(2020年北京大学强基计划测试题)函数


2.(2021年清华大学强基计划测试第10题)已知函数设f(x)的最大值为M,最小值为m,则( ).
3.(2020年上海交通大学强基计划测试第24题)函数在上的最小值为 .
4.(2022年清华大学新领军TACA数学二试题第2题)已知正实数a,b满足a+2b=1,I为的最小值,则[I]= .
注:若实数a满足n≤a 二元函数最值问题历来是高考、竞赛、高校强基计划测试等选拔性考试的热点,题目一般是函数、方程与不等式等知识的综合应用试题,技巧性较强.为此,教师要引导学生深刻剖析题设条件,挖掘隐含信息,揭示问题本质,捕捉解题灵感,构建解决方案.学生在感知确认、抽象概括、合情推理、操作运算等思维活动中,多角度、多层次地思考问题,综合运用各种方法,提出新视角、新观点、新设想,逐步学会有逻辑地思考数学问题.
六、结语
