基于海量数据分析的电力工程动态智能监控技术研究

李 玺，张维堂，常健翔，李敏银

（1.国网甘肃省电力公司，甘肃兰州 730030；2.国网陇南供电公司，甘肃陇南 746000；3.国网庆阳供电公司，甘肃 庆阳 745000）

科学合理、高效有序地推进电力工程建设，是促进经济迅速发展的重要举措之一[1-2]。近年来随着电力工程的不断推进，发输配变等各环节自动化、信息化的逐步完善，电网公司对于电力工程投资的精准性、工程建设的质量等要求也越发严苛。因此，对于电力工程监控的重要性也日益凸显[3-4]。在该工程建设过程中，积累了海量的工程数据。而如何结合大数据分析技术实现电力工程的智能化监控，成为了亟待解决的问题[5-7]。大数据分析技术在电力领域的应用主要集中在负荷预测、故障诊断与运维检修等方面[8-10]，其在电力工程监控方面的应用仍然较少。

针对此问题，该文将大数据分析技术应用于电力工程监控中，并实现了对该工程的动态智能化监测，进而为电网公司电力工程的高效投资、精益管理与高质量发展建设提供了保障。

1 动态智能监控体系架构

文中通过对电力工程数据的综合分析，从进度、成本及质量三方面构建了工程动态智能监控指标体系。如图1 所示，该体系涵盖了可研、初设、施工与竣工验收等不同阶段的20 个监控指标。

图1 电力工程动态智能监控指标体系

2 监控算法设计

该文基于标度法（Scaling Method，SM）[11]与先验算法（Apriori）[12]提出了电力工程动态智能监控算法的框架设计方案，其流程如图2 所示。

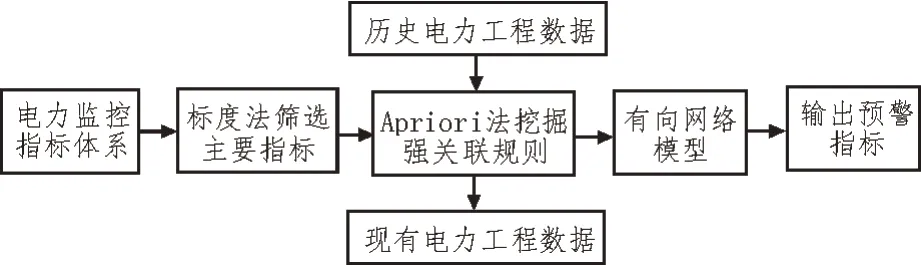
图2 基于SM-Apriori的电力工程智能监控算法

首先在电力工程监控指标体系的基础上，采用标度法筛选出工程项目的主要影响指标；然后在Apriori 算法的基础上，利用历史电力工程数据挖掘监控指标之间、监控指标与项目总目标之间的强关联规则；之后，构建电力工程动态智能监控的有向网络模型；最终将现有工程数据输入该模型，从而获得电力工程的监控预警结果。

2.1 基于SM的主要影响指标筛选

为实现电力工程的精准监控，此次采用标度法从中筛选主要影响指标。算法包括以下几个步骤：

1）通过咨询行业专家，采用数字1-9 来描述第k层指标相对于第k-1 层指标的重要程度。不同数字标度的含义，如表1 所示。

表1 1-9标度值的含义

2）构建第k层n个指标相对于第k-1 层元素的判别矩阵可表征为：

式中，mij为指标的标度与指标标度的比值。其计算方式为：

3）计算判别矩阵的最大特征根及对应的特征向量：

式中，λmax和W(k)分别为M(k)H的最大特征根与对应的特征向量。

4）查找表2，并根据式（4）进行一致性校检。

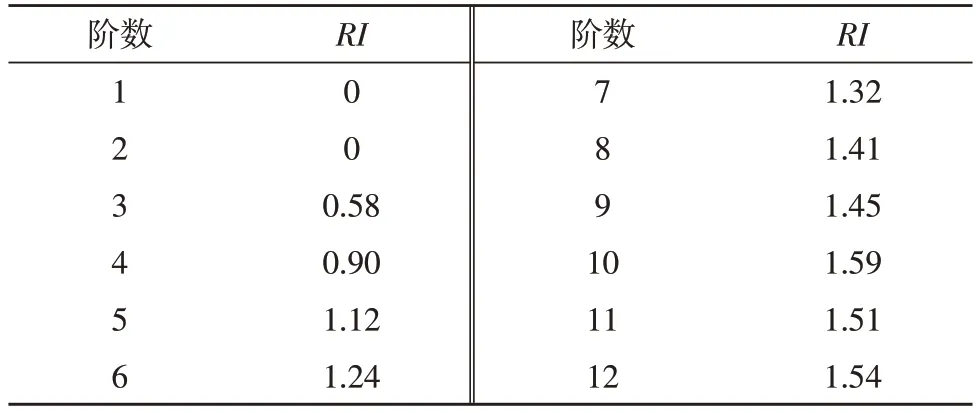
表2 RI取值表

式中，RI为平均随机一致性系数，其可根据阶数n的大小查找表2 获取；CR为随机一致性参数，且当CR＜0.1 时，满足一致性校检。

5）计算各监控指标的权重系数。

首先对W进行标幺化，得到第k层指标相对于第k-1 层指标的权重向量W*(k)：

进一步计算第k层指标相对于目标的权重向量Q(k)：

式中，Q(k-1)为第k-1 层相对于目标的权重向量。

2.2 Apriori算法

在电力工程N条数据样本中，监控指标a的所有取值构成其项集A，监控指标b的所有取值构成项集B。

支持度可描述项集A与B中监控指标同时出现的比例：

式中，S(A→B)为项集A对于项集B的支持度，λ(A,B)则为项集A与B同时出现的样本数。

置信度则是描述在项集A发生的前提下，项集A与项集B中监控指标出现的概率：

式中，C(A→B)为项集A对于项集B的置信度；λ(A)为项集A出现的样本数。

而提升度则是描述项集A出现导致项集B出现的概率：

式中，L(A→B)为项集A对于项集B的提升度；λ(B)为项集B出现的样本数。

当支持度、置信度及提升度均满足以下最小阈值的条件时，说明项集之间存在强关联关系；反之，则说明项集之间的关联关系较弱。

式中，Sσ、Cσ和Lσ分别为支持度、置信度与提升度的最小阈值。

仅满足式（10）中最小支持度阈值的项集，便是频繁项集。

Apriori算法利用了频繁项集的两个重要性质[13]：

1）频繁项集的所有非空子集也为频繁项集；

2）非频繁项集与其他项集或事件的并集也是非频繁项集。

Apriori 算法的核心思想是[14-15]：从最小的项集出发构建候选项集，计算支持度并筛选出频繁项集；然后通过连接操作形成下一阶项集作为新一轮的候选项集，且再次计算支持度，并筛选出频繁项集；如此经过多轮循环，直至无法生成新的频繁项集为止；最终计算所有频繁项集的置信度及支持度，进而输出项集之间的强关联规则。

基于Apriori 算法的电力工程动态监控算法，如图3 所示[16]。

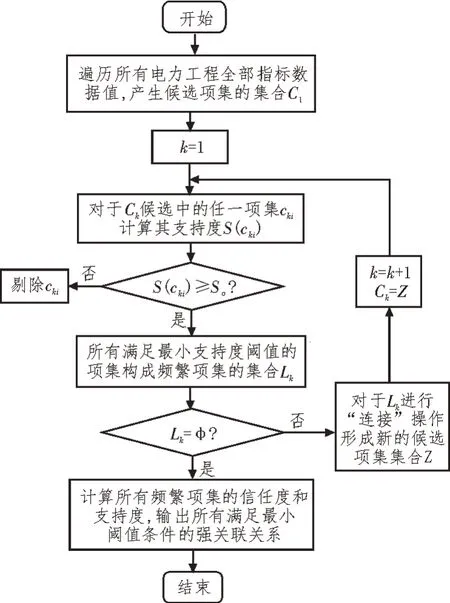
图3 基于Apriori算法的关联规则挖掘

2.3 构建有向网络模型

有向网络模型可表示为G(Vi,Vj,θij)，关联规则Vi→Vj对应的是有向网络模型中的一条有向边。其起点与终点分别为监控指标Vi及Vj，边θij的权重则为关联规则的置信度。有向网络模型的构建示意图，如图4 所示。

图4 有向网络模型构建示意图

2.4 监控预警指标获取

收集现有电力工程项目各监控指标的偏差情况，计算偏差置信度为：

式中，αi为第i个指标的偏差置信度，di为现有电力工程项目中第i个监控指标出现偏差的项目数量，D则为现有电力工程项目总数。

以每个指标为起点，并根据有向网络模型，沿着监控指标间的加权边计算每个监控指标误差导致项目最终出现偏差的置信度：

式中，φi为第i个监控指标偏差导致项目最终出现偏差的置信度；q为目标节点。

最后，判断φi是否大于监控阈值φmax的指标。若是，则判定该监控指标存在风险，并将其作为预警结果输出。

3 算例分析

该文从某实际电力工程业务系统中，导出共2 500 条数据作为实验样本。预处理时对于某个监控指标：其中若存在负向偏差，则该指标值记为1；否则，该指标的值为0。同时，在Matlab 平台上对所设计的监控算法进行仿真验证。

3.1 关联规则挖掘结果

将支持度、置信度及提升度的阈值分别设置为0.05、0.4 和1，通过Apriori 算法进行监控指标之间的关联规则挖掘，且总共得到22 条强关联规则。所有强关联规则的相关指标，如图5 所示。

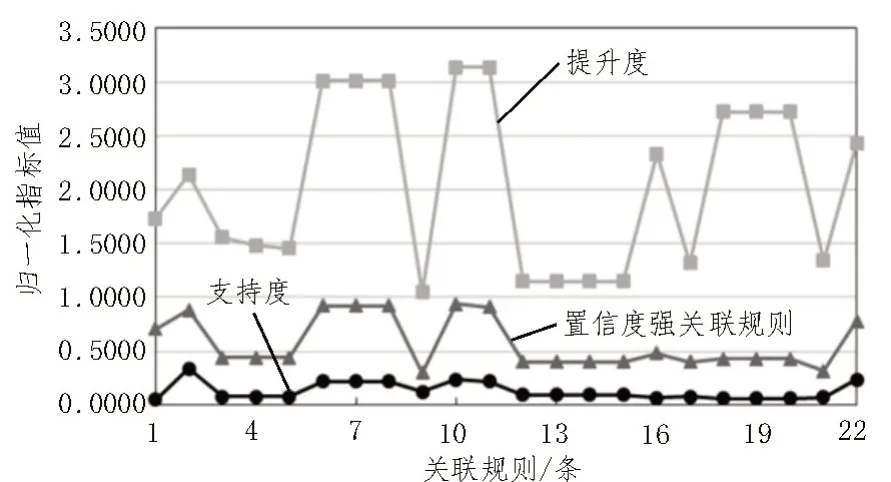
图5 强关联规则的相关指标

以第1 条强关联规则“项目申报及审批进度（项集A）→开工时间（项集B）”为例进行说明分析，其3 个指标值分别为0.051 3、0.705 9 和1.729 4。上述指标说明：“项目申报及审批进度”和“开工时间”同时出现偏差的比例为5.13%，且在“项目申报及审批进度”出现偏差的项目中，有70.59%的项目在“开工时间”指标上也出现了偏差。此外，“项目申报及审批进度”出现偏差还导致“开工时间”出现偏差的概率提升了1.729 4 倍。

3.2 监控预警应用结果分析

将该文方法应用于某电网公司现有的124 个电力工程项目的动态智能监控中。通过数据收集获得各项监控指标的偏差置信度，再利用有向网络模型计算其导致项目出现偏差的可能性。测试将项目偏差置信度的阈值设置为20%，以此判决是否发出预警。监控预警应用结果，如表3 所示。

表3 监控预警应用结果

由表可知，物资配送进度a5、开工时间a6、完工时间a8、竣工结算b6以及隐蔽工程验收全覆盖c45 个监控指标，有较大可能会导致项目在进度、成本与质量方面存在偏差。故应加强对此类环节的管控，以降低项目偏差的风险。

4 结束语

该文利用SM 和Apriori 算法对海量电力工程数据进行处理与分析，实现了电力工程的动态智能监控。数值实验结果表明，该算法能够挖掘不同监控指标对电力工程项目偏差风险的内在关联关系。同时在现有电力工程的监控应用中，还发现物资配送进度、开工时间等监控指标易导致项目偏差风险的增加，因此需加强对上述指标相关环节的管控。但目前该方法仅能识别某些环节的风险，而无法实现更加精细化的风险识别定位，这将在后续研究中开展。