四面体图与完全图字典积的平均首达时间

倪 琦，周 环，吕宁宁，潘向峰

(1.安徽大学 数学科学学院,合肥 230601；2.安徽工业经济职业技术学院公共教学部，合肥 230051)

平均首达时间是有限随机游走的重要性质参数之一,被广泛用于各种网络的动态研究,国内外学者致力于研究其数值计算和理论表达式。[1]陈海燕[2]等通过多项式方法推导出了强连通非周期有向图上随机游走的平均首达时间的表达式,并利用这个新的公式给出了强正则图与完全图的二元运算(弱直积、直积、卡氏积)生成图上的平均首达时间。文献[3]和[4]分别给出了Johnson 图J(n,3)的特征值与相应的特征重数。王志俊[5]等确定了图G 与连通正则图H 的字典积图的特征多项式和邻接谱。倪湘钧[6]等研究了强正则图与完全图的字典积的平均首达时间。图的字典积是一种二进制运算，它可以从旧图生成新图。与笛卡尔积和图的强积等其他二元运算不同,图的字典积不满足交换律,其特征多项式一般不能由两个组成图的特征多项式确定。[5]

受到上述文献的启发,基于连通的强正则图是直径为2 的一类距离正则图这一事实,本文继续深入研究直径为3的一类距离正则图Johnson图J(n,3)与完全图字典积的平均首达时间和电阻距离以及度积基尔霍夫指数、凯梅尼常数等图不变量。文献[7]阐述了基尔霍夫指数近年来的研究情况。这里只讨论无向的简单连通图,如无特殊说明将遵循文献[8]中的符号和术语。

1 预备知识

定义1[9]Johnson 图J(n,m)定义如下:其中n是N元集合N={1,2,3,…,n}的元素个数,顶点集V(J(n,m))由N 的m元子集构成,显然图中有个点,其中任意两点相邻当且仅当它们中仅有一个元素不同。易见J(n,m)是m(n-m)正则图,其直径为min(m,n-m)。例如,J(n,0)是一个单点;J(n,1)是一个完全图Kn;J(n,2)是三角形图T(n),见图1。

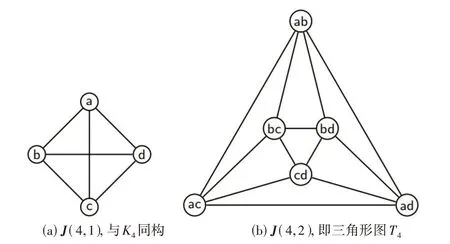
图1 n=1和2时的Johnson图

Johnson 图J(n,3)的直径为min(3,n-3)。本文主要研究Johnson 图G=J(n,3)(n≥6)与完全图字典积的平均首达时间,以下对J(n,3)不再指明n≥6。

如果让d(x,y)表示两个顶点x,y之间的距离,Δ(x,y)表示与x,y都相邻的顶点数量,n2(x)是与点x距离为2的点y的数目,A(G)是G的邻接矩阵,简记为A,那么特征为n的Johnson图G具有以下性质[3，10]:

2)G是连通且正则的,正则度为3(n-3)；

3)n2(x)=(n-3)(n-4),∀x∈V(G)；

4)A(G)的不同特征值是3(n-3),2n-9,n-7,-3,其特征重数分别为1,n-1,

5)如果d(x,y)=1,那么Δ(x,y)=n-2；

6)如果d(x,y)=2,那么Δ(x,y)=4。

由文献[3]和[11]可知,矩阵A满足等式即Hoffman多项式h(A)=J,即

其中：J是全1矩阵；I是单位矩阵。

因此

这里表示Ak的ij元素。

命题设H是m阶完全图,其邻接矩阵特征值为m-1,-1,对应重数分别为1,m-1。

定义2两个图G和H的字典积G[H]具有顶点集V(G)×V(H),其中(u1,v1)与(u2,v2)相邻当且仅当u1和u2在G中相邻,或u1=u2且v1和v2在H中相邻。

定 理1[5]设图G的特征值为λ1,λ2,λ3,…,λn(λ1≥λ2≥λ3≥…≥λn),正则图H的特征值为μ1,μ2,μ3,…,μm(μ1≥μ2≥μ3≥…≥μm),则相应字典积图G[H]的特征值为λ1m+μ1,λ2m+μ1,λ3m+μ1,…,λnm+μ1,μ2,μ3,…,μm,且μ2,μ3,…,μm的重数等于n。

本文主要讨论的是Johnson 图J(n,3)与完全图字典积的平均首达时间,利用定理1,G[H]仅有五个不同的邻接谱:3mn-8m-1,2mn-8m-1,mn-6m-1,-2m-1,-1,且对应重数[4]分别为1,n-1,。J(n,3) 的例子见图2。

定理2[2]设G是一个强连通非周期有向图,则G上随机游走是不可约非周期的马尔科夫链,P是概率转移矩阵,存在多项式f(x)=xn+a1xn-1+a2xn-2+…+an-1x+an,其中f(1)≠0 且f(P)是一个行向量相同的矩阵,那么∀i,j∈V(G),有

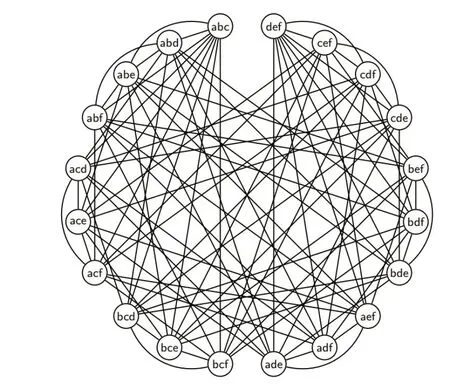
图J(6,3)

其中：π是马尔科夫链的平稳分布；πj是其第j个分量。

由于P是图上的概率转移矩阵,即不可约非负的随机矩阵,因而1是P的最大特征值,且重数为1,从而可得P的极小多项式为q(x)=(x-1)f(x),故研究满足定理2条件的f(x)只需研究q(x),进一步研究该字典积图的平均首达时间。[6]

下面字典积图G[H]中任意两点的电阻距离可由任意两点间的平均首达时间给出。

定理3[12]设G是连通图,边数为m,则对∀i,j∈V(G),有

对于连通图G,考虑N(G)=显然它是实对称矩阵,该连通图的度积基尔霍夫指数可由N(G)的特征值表示,其中D(G)=diag(d1,d2,…,dn),A(G)是图G的邻接矩阵,其第i行第j列的元素为1当且仅当点i与点j相邻,否则为0;di是顶点i在图G中的度[6]。

定理4[13]设G是一个阶数为n且边数为m的连通图,则Kf*(G)=其中λi表示N(G)的特征值,λ1≥λ2≥λ3≥…≥λn。

由于字典积G[H]为3mn-8m-1正则图,故D(G[H])=diag(3mn-8m-1,3mn-8m-1,

…,3mn-8m-1),从而N(G[H])=A(G[H])。又 由A(G[H]) 的特征值可知N(G[H])的特征值为

定理5[14]设G是一个具有m条边n个点的连通图,则Kf*(G)=2mKe(G)。

定理6[15]设G是一个具有m条边n个点的连通图,则(1 -λk)=2mτ(G),其中λi是N(G)的特征值且满足λ1≥λ2≥λ3≥…≥λn,τ(G)是G的生成树数目。

2 主要结果

当无向图是连通且非二部的,我们也可以应用定理2 来计算平均首达时间[2]。J(n,3)是一类Johnson图,它是一种距离传递图,具有多种良好的性质。很显然Johnson 图J(n,3)(非二部)与完全图的字典积上的简单随机游走是不可约非周期的马尔科夫链,下面我们给出的J(n,3),都默认它是非二部的。

下面给出Johnson 图J(n,3)与完全图的字典积中任意两点间的平均首达时间。设G是特征为n的Johnson 图J(n,3),A是G的邻接矩阵。设H是Km,则G[H]是一个3mn-8m-1 正则连通图,阶为。由文献[5]可知,G[H]的邻接矩阵表达式为A(G[H])=A(G)⊗J+I⊗A(H),其中J表示全1 矩阵,⊗表示张量积。根据定理1,G[H]仅有五个不同的特征值:3mn-8m-1,2mn-8m-1,mn-6m-1,-2m-1,-1,极小多项式为(x-3mn+8m+1)(x-2mn+8m+1)(x-mn+6m+1)(x+2m+1)(x+1)。

因为H是Km,所以对于∀v1,v2∈V(H),v1和v2相邻,于是只需对u1,u2进行分类讨论。根据定理2,可以得到如下结论。

定理7对G[H]上的简单随机游走,对∀i=u1v1,j=u2v2∈V(G[H]),有

(1)若u1与u2邻接,i与j邻接,则

(2)若u1与u2不邻接且d(u1,u2)=2,i与j不邻接,则

(3)若u1与u2不邻接且d(u1,u2)=3,i与j不邻接,则

(4)若u1=u2,i与j邻接,则

证明设P是G[H]上简单随机游走的概率转移矩阵,则P=A,极小多项式为

由于q(x)=f(x)(x-1),因此

经过计算可得

而A3(G[H])的对角线子矩阵为

其非对角线子矩阵为

下面，对i,j分情况讨论:

(1)若u1与u2邻接,i与j邻接,则由上面的式子及(1)、(2)和(3)

因此,

(2)若u1与u2不邻接且d(u1,u2)=2,i与j不邻接,则

(3)若u1与u2不邻接且d(u1,u2)=3,i与j不邻接,则

(4)若u1=u2,i与j邻接,则

因为该字典积图为无向图,所以EiTj=EjTi。对任意i,j∈V(G[H]),可以得到两点间的电阻距离公式

接下来,利用计算出的G[H]的特征值,推导出与[G[H]有关的一些图不变量:度积基尔霍夫指数、凯梅尼常数以及生成树个数。此外,基于G[H]上任意两点间的平均首达时间,给出G[H]上任意两点间的电阻距离。图G和图H的参数确定了这些图不变量。文献[12]刻画了度积基尔霍夫指数与N(G)特征值之间的关系。

定理8设G是具有特征n的Johnson图J(n,3),H为m阶完全图,其字典积G[H]的度积基尔霍夫指数为

又由A(G[H])的特征值可知N(G[H])的特征值为

对应重数分别为

则由定理4可得

由上可知,对于凯梅尼常数,利用定理5和定理8可以直接推出。

定理9设G是具有特征n的Johnson图J(n,3),H为m阶完全图,其字典积G[H]的凯梅尼常数为

定理10设G是具有特征n的Johnson图J(n,3),H为m阶完全图,其字典积G[H]的生成树数目是

其中τ(G[H])是字典积G[H]的生成树的数目,k1=n-1,k2=。

2 结束语

本文通过研究文献[2]中赋权有向图上随机游走平均首达时间的表达式以及文献[5]中两个简单图的特征值与其字典积的特征值的关系,在文献[6]研究具有三个不同特征值的强正则图(非二部)与完全图的字典积的基础之上,根据Hoffman 多项式进一步去研究具有四个不同特征值的Johnson 图J(n,3)和完全图字典积的邻接矩阵及其特征值,再利用多项式方法推导出所生成的字典积上两点间的平均首达时间、电阻距离以及一些重要的图参数。