图神经网络研究与进展

许荣斌， 许智强， 王吉祥， 谢 莹*

( 1. 莆田学院 机电与信息工程学院， 福建 莆田 351100；2. 福建省金融信息处理重点实验室， 福建 莆田 351100 )

0 引言

近年来， 神经网络模型成功地推动了模式识别和数据挖掘领域的相关研究。 受卷积神经网络(CNN)、 递归神经网络(RNN)和图自编码器(GAE)等端到端深度学习模式的影响， 目前机器学习方法已具备自动提取特征的能力[1]。 深度学习的成功， 部分归因于计算资源如Graphics Processing Unit(GPU)的快速发展、 大规模训练数据的可用性以及深度学习从结构化欧式空间数据(如图像、 文本和视频) 中提取潜在表示的高效性。 以图像数据为例， 研究者可以在欧式空间中将图像数据表示为正则网格， CNN 能够利用图像数据的平移不变性、 局部连接性以及组合性， 提取出有意义的特征。 这些特征不仅可以与整个数据集共享， 还可用于各种图像分析工作[2]。

尽管深度学习在捕捉欧式空间数据的潜在表示方面表现出色， 但随着数据以非欧式空间(图结构形式)表达的激增， 深度学习在越来越多应用场景下的适用性面临挑战。 例如， 在电子商务中， 使用基于图结构的推荐系统可以利用用户和产品之间的交互实现精确推荐[3]； 在化学研究领域， 分子被建模为图结构， 再确定其生物活性以进行药物发现[4]； 在引文网络中， 文章通过引用关系相互链接， 再将其分类为不同的组[5]。图结构数据的复杂性对现有机器学习算法产生了重大挑战。 由于图结构往往不规则且节点数量和邻居数量不确定， 各种基础操作(如卷积)在图像中容易实现， 在图结构上却非常复杂。 此外，现有机器学习算法的核心假设是实例之间相互独立。 对于图结构数据而言， 由于每个实例都受到与其他实例相关的各种链接(如引用、友谊、交互等)的影响， 该核心假设不再成立[6]。

在深度学习方法扩展到图结构数据的研究进程中， 受CNN、 RNN 和GAE 的启发， 过去几年已形成新的泛化和重要操作的定义， 以处理复杂的图结构数据。 例如， 可以将图结构卷积泛化为二维卷积。 如图1 所示， 可将图像视为图结构的一种特殊情形， 其中像素由相邻像素相连。 与二维卷积类似， 可通过对节点的邻域信息加权平均来执行图结构卷积。 CHEN 等重点介绍了若干图神经网络结构[1]， 专注于解决网络嵌入问题。 Li等将图结构网络定义为从关系数据中学习的构建块， 以统一图神经网络框架[5]。 Scarselli 等首次阐述图神经网络(GNN)[7]， 概述了非欧式空间中针对图和流形结构的深度学习方法。 Lee 等对应用不同注意机制的图神经网络进行了研究[8]。本文概述了当前最新的图神经网络技术， 详细阐述每种类型的图神经网络的代表性模型和性能比较； 同时， 收集了丰富的图神经网络资源，包括基准数据集、 开源库和实际应用； 最后，研讨图神经网络的理论进展， 分析了现有方法的局限性， 并提出了三个可能的未来研究方向: 模型深度、 平衡伸缩性和异构性/动态性的讨论。

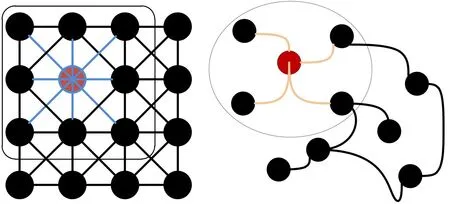
图1 欧式空间数据(左)与非欧式空间数据(右)

1 图的定义及表示

1.1 图的基本概念

本文使用大写黑斜体字符来表示矩阵， 使用小写黑斜体字符来表示向量。

定义1(图) 图表示为G＝(V，E)， 其中V是顶点或节点的集合，E是边的集合。vi∈V表示V中第i个节点。 节点v的邻域定义为N(v)＝{u∈V ｜(v，u)∈E}。 邻接矩阵A∈Rn×n中，如果vi和vj之间有边， 则Aij＝1， 否则Aij＝0。图可能具有节点属性X， 其中A∈Rn×d是节点特征矩阵。

定义2(有向图) 有向图是节点间有方向的图。 无向图被视为具有逆方向对的一对边的特例， 如果两个节点相连， 则这两个边具有逆方向。 当且仅当邻接矩阵对称时， 图是无向的。

1.2 基本图谱论

图论傅里叶变换是一种基于图拉普拉斯矩阵的离散傅里叶变换， 并已成为图信号分析的一项基本工具。 它的主要作用是将图信号从空域(顶点上) 的f(t) 转换到谱域(频域)的F(ω)，能够将图信号分解成不同频率分量的线性组合。 在传统的(连续) 傅里叶变换中， 此方法已被广泛应用于信号处理和分析。 相对而言， 图论傅里叶变换更适用于处理包含图结构的数据:

式(1)中，ω为角频率，t为时间， e-iωt是基函数。 此基函数与拉普拉斯算子的关系如下:

此形态与特征值分解方程Lu＝λu一致。 因此，e-iωt可以看作拉普拉斯算子的特征函数， 而ω则与特征值相关。 图拉普拉斯矩阵对应着图结构上的拉普拉斯算子。 此时把拉普拉斯算子的特征函数换成拉普拉斯矩阵的特征向量， 即可把傅里叶变换迁移到图结构上进行工作。

对于一个具备个顶点的图G， 可将它的拉普拉斯矩阵L作为傅里叶变换中的拉普拉斯算子。L是实对称矩阵， 对其进行如下特征分解:

式(3)中，U是一个正交化的特征向量矩阵UUT＝UTU＝I，I是单位矩阵，T 为转置操作，Λ是特征值的对角阵。U提供了一个具有完全正交性的图结构上基底，对图结构上的任意向量f，均可通过U中特征向量的线性组合进行表示:

式(4)中，ul是U的第l个列向量， 也是对应特征值λl的特征向量。 采用这些特征向量来取代原先傅里叶变换式(1)中所使用的基底， 从而将原本的时域转换为顶点上的空域。 经过这样的处理， 图结构上的傅里叶变换便得以重新定义:

式(5)中，λl表示第个l特征值，f(i)对应第个节点上的特征，ul(i) 表示特征向量ul的第i个元素。 推广到矩阵形式为UTf。

2 图神经网络模型

本章具体阐述将深度学习扩展到图结构数据上的重要图神经网络模型。 这里将图神经网络分为基于谱域的模型和基于空域的模型。

2.1 基于谱域的图神经网络

谱域上的图卷积在深度学习向图学习发展的历程中具有重要的作用。 在该领域中， 谱域图卷积网络、 切比雪夫网络与图卷积网络因其代表性被广泛推崇。

(1)谱域图卷积网络

图卷积网络模型可以视为对图信号x的三个步骤变换:

①对空域中的图信号x进行图论傅里叶变换， 从而得到其傅里叶系数表示F(x)＝UTx；

②在谱域中定义可参数化的卷积核gθ， 并将其作用于傅里叶系数形式的图信号， 得到卷积后的图信号gθUTx；

③将卷积后的谱域信号进行图论傅里叶逆变换， 从而将其转换成空域中的图信号表示F-1(gθUTx)＝UgθUTx。

最终得到简洁的图卷积形式:

式(6)中，UTg整体为一个可参数化的卷积核θ。虽然此前模型为谱域图卷积指明了方向， 但仍存在改进空间。 实现该类神经网络， 需要付出高昂的成本:

①计算图拉普拉斯矩阵的特征向量， 其复杂度为O(n3)(其中n为节点数量) ， 在大规模图中计算可行度低；

②每次前向传递， 需要进行的矩阵运算， 操作非常耗时；

③每层需要n×dl×dl＋1个参数来定义卷积核， 当图规模较大时， 参数过多造成计算量大且较难拟合；

④该谱域卷积方式在空域上没有明确意义，无法明确地局部化到顶点上。

接下来介绍推动谱域图卷积实用化的模型。

(2)切比雪夫网络

为了突破先前提出的谱域图卷积网络的限制， 研究者Defferrard 等提出了一种新的谱域图卷积网络[2]。 该网络实现了快速局部化和低计算复杂度， 采用了切比雪夫多项式的展开逼近方法。 切比雪夫网络提出了更先进的加速方案， 即将gθ(Λ) 近似为阶切比雪夫多项式的截断形式:

式(7) 中，Tk是k阶切比雪夫多项式，＝2Λn/λmax-In是对角矩阵， 它可以实现将特征值对角化， 并将其映射至区间[- 1，1]。 切比雪夫多项式被选用的原因在于其优秀的性质， 即可实现循环递归求解:

考虑从初值T0＝1，T1＝x出发， 利用递推公式(8) 进行递推， 可以轻松地求解k阶系数Tk的取值。 对于L， 引入＝2L/λmax-In式， 以实现其K次多项式运算。 该式具有保持K-局部化(即节点仅受其周围的K阶邻居节点影响) 的特性， 有助于实际应用中的性能和效果提升。 在实际操作中， 采用对称归一化拉普拉斯矩阵Lsym来替代原来的L， 以更好地满足现实应用中的需求。

(3)图卷积网络

基于切比雪夫网络的设计思路， Kipf 等提出了一种经典的图卷积网络， 进一步简化网络结构并减少计算量[3]。 此方法将切比雪夫网络中的多项式卷积核限定为1 阶， 使得图卷积的计算可以近似成一个关于对称归一化拉普拉斯矩阵的线性函数。 尽管这样的限制带来了节点只能被周围1 阶邻接点影响的问题， 但是通过叠加这样多层的图卷积层， 可以将节点的影响力扩展到阶邻居节点， 同时也让节点对阶邻居节点的依赖变得更加灵活。 实践中， 叠加多层1 阶图卷积和节点扩散也取得了良好的效果。 由于拉普拉斯矩阵的最大特征值可以近似取λmax＝ 2， 1 阶图卷积可以写为:

式(10) 中，是参数矩阵，Z∈Rc×d是图卷积之后的输出。

现实应用常常将多层图卷积叠加以构建一种图卷积网络(如图2 所示)。

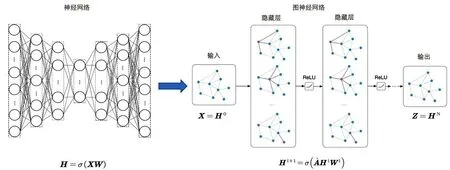
图2 从神经网络到图神经网络

该网络的第1 层用H1表示该层节点矩阵， 用W1表示该层的参数矩阵。 定义符号为卷积操作， 则基于激活函数σ(·)的每层图卷积定义为:

尽管谱域图神经网络有着坚实的理论基础，并且在实际任务中已经取得了显著的成功， 但其存在一些明显的局限性。 首先， 许多谱域图神经网络需要对拉普拉斯矩阵进行分解以获取特征值和特征向量， 这是一项计算复杂度较高的操作。虽然切比雪夫和图卷积网络在简化了处理步骤之后已经不需要这一步， 但是它们在计算时仍然需要将全图存入内存， 这会消耗大量的存储空间。此外， 谱域图神经网络的卷积操作通常作用在图拉普拉斯矩阵的特征值矩阵上， 这些卷积核参数无法迁移到另一个图结构上。 因此， 谱域图神经网络通常只能应用在一个单独的图结构上， 而这会大大限制这些模型的跨图学习和泛化能力。

谱域图神经网络模型通常具有高度的复杂性， 并且受到较多局限， 因此相对于空域图神经网络， 其后续研究相对较少。 然而， 图谱分析提供了一种非常有效的分析工具， 并且谱域图卷积的研究始终没有停止。 例如， 一些研究在图小波网络中引入了更高级的滤波器， 谱小波与积分算子设计了更为稳定的滤波器[9]； GRAND＋＋定义一种无谱方法求解一小组稀疏、 对称和条件良好的线性系统， 并且忽略了拉普拉斯或核谱的评估[10]。 这些研究为谱域图卷积的发展提供了新的思路和探索方向。

2.2 基于空域的图神经网络

空域图卷积神经网络比其他形式的网络更早被广泛应用， 其核心理念在于对邻接点的空域信息进行直接聚合， 这种理念非常贴合人的直觉。此类方法的关键在于如何将欧式空间中的卷积操作扩展到图结构上。 考虑定义一种可在邻居数量不同的节点上进行操作的方法， 并保持类似于GNN 中的权重共享特性。

(1)GraphSAGE

早期图神经网络及图嵌入方法存在缺陷: 在同一图结构上进行测试时， 对于未参与训练的节点， 是无法获取其嵌入表示的。 这类方法主要基于直推式学习框架， 即假设测试节点与训练节点处于同一图结构中， 并且在训练过程中考虑了图结构中所有节点。 图卷积网络主要应用于半监督/直推式学习， 但也可以改进为归纳式学习。Hamilton 提出了一种基于归纳式学习的图神经网络模型——GraphSAGE， 该模型主张通过共同聚合邻接节点信息的函数来获取节点的嵌入表示[11]。 在训练模型时， 只需通过学习该聚合函数， 即可实现对未知节点的泛化能力。 目前后续研究主要聚焦在如何定义该聚合函数以及基于此定义可学习的图神经网络。

(2)消息传递神经网络

无论是图卷积网络还是GraphSAGE 模型，空域图神经网络都采用某种形式的邻居节点进行信息传递， 以实现节点状态的更新。 实际上， 几乎所有的图神经网络都可以视为某种形式的消息传递， 因此消息传递神经网络作为空域卷积的形式化框架被提出[12]。 类似于GraphSAGE 的聚合与更新操作， 消息传递神经网络将图神经网络的消息传播过程分解为两个步骤: 消息传递和状态更新。

(3)图注意力网络

注意力机制(Attention Mechanism)已经成为许多深度学习模型必不可少的模块， 例如在自然语言处理的机器翻译任务中。 最近流行的大规模预训练模型ChatGPT[13]也是基于全注意力结构Transformer[14]构建的。 简而言之， 注意力机制通过给不同输入元素赋予不同的权重， 来区分它们的重要性， 从而抽取更关键的信息， 提高模型的效果。 因为在图结构中各节点的重要性不同， 因此可以将注意力机制应用于图神经网络， 形成图注意力网络[15]。

2.3 图同构网络

图神经网络取得优秀成就与它的表达力密切相关， 图同构网络是图神经网络表达力的经典研究——Weisfeiler-Lehman 测试下的重要模型。 图同构问题旨在判别两个图在拓扑结构上是否相同。 Weisfeiler-Lehman 测试是一种有效的、 近似的图同构检验方法。 首先， 通过聚合每个节点以及其邻居的标签， 再通过哈希函数生成新的节点标签， 之后不断重复这个过程， 直到每个节点的标签达到稳定状态。 如果在某些迭代中， 两个图的节点标签不同， 则可以判定这两个图是不同的。 在Weisfeiler-Lehman 测试中， 进行次迭代后，会得到一个高度为的节点子树， 如图3 所示。

图3 K 次迭代之后的Weisfeiler-Lehman 子树

此为一棵高度为K＝2、 根节点为1 的子树模式。 右侧为展开的子树模式中节点的重复状态。 Weisfeiler-Lehman 子树是核方法中的常用工具， 用于计算两个图的相似度。 相关工作证明了Weisfeiler-Lehman 测试可以作为图神经网络表达能力的上限[16]。

总而言之， Weisfeiler-Lehman 测试和图同构网络是探索图神经网络表达能力问题的重要里程碑[17]， 对推动图相关领域的发展具有重要意义。

3 图神经网络公开资源

图结构数据的广泛应用使得图神经网络在许多领域得以大放异彩。 本节将分别介绍基准图数据集、 评估任务， 并详细探讨图神经网络在各个领域的实际应用。

3.1 基准数据集

在图神经网络中， 数据集通常被归为四大类， 即引用网络图结构、 生物化学图结构、 社交网络图结构和其他类型图[3]。 常用的基准数据集如表1 所示。 其中， 引用网络图是由文章引用关系构成的网络； 生物化学图是化合物或蛋白质等生物分子之间相互作用所构成的网络； 社交网络图则是包含个人、 用户或其他实体及其联系的网络； 其他类型如手写体数据集(MNIST)、 语言学习项目中获得的知识图(NELL)结构、 分子图(MUTAG)结构等。

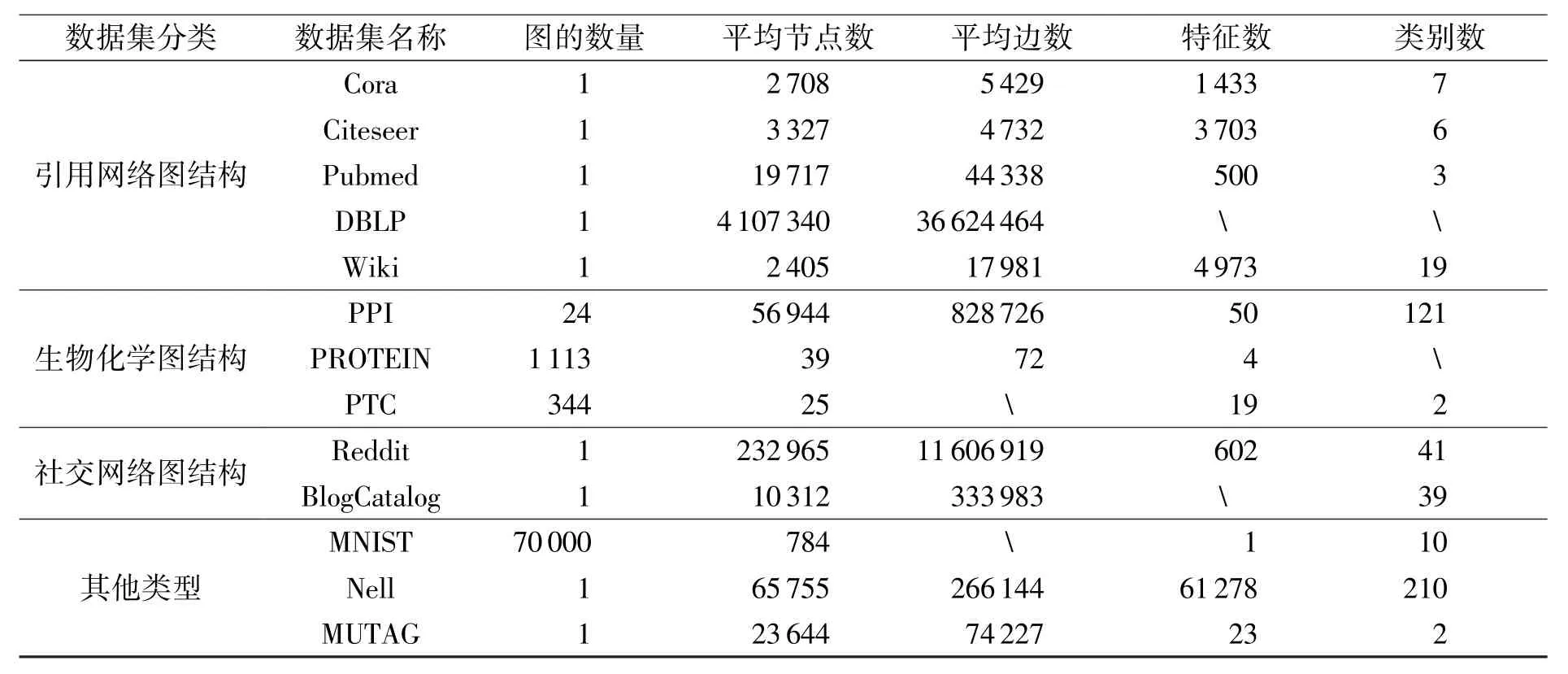
表1 常用的基准数据集

3.2 评估任务

节点分类、 边分类和图分类是评估图神经网络性能的常见任务。

(1)节点分类

在节点分类任务中， 通常采用基准数据集来进行训练、 验证和测试的标准分割。 通过多次运行， 可记录平均准确率或F1 得分。 使用同一种训练、 验证和测试分割方案， 可能会低估模型的泛化误差。 此外， 由于不同的方法采用了不同的训练技巧， 例如超参数调整、 参数初始化、 学习率衰减和早停等， 因而可能存在有偏差的分类结果[18]。

(2)边分类

包括边的分类、 链路预测等。 如推荐系统领域， 利用图神经网络对用户之间的关系进行分类， 可以帮助推荐系统更加准确地推荐内容。 在边分类中， 需要考虑边的结构信息， 也需要考虑两个节点之间的结构信息和边的拓扑结构。 例如两个节点的共同邻居数、 边的传递性等， 这些结构信息可以作为边的特征。 进一步考虑联合边和节点的特征， 这可以提供更丰富的上下文信息，帮助提高边分类的准确性[19]。

(3)图分类

在图分类任务中， 存在实验设置上的歧义和不一致性。 通常采用十折交叉验证方法来评估模型， 但这种方法容易出现同时在测试集中进行模型选择和模型评估的问题。 为了解决这一问题，Errica 等提出了内部保留集技术和双重交叉验证方法， 并使用这两种方法来相对公平地比较了图神经网络方法[20]。

(4)任务所涉及开源库

Amazon DGL(Deep Graph Library)提供了快速实现图神经网络模型的方案[21]。 Fey 等在PyTorch 中发布了名为 Kumo PyG ( PyTorch Geometric)的学习库， 包含可实现多种图神经网络模型的代码[22]。 除此之外， 还有TensorFlow图神经网络[23]等开源库可供选择。

3.3 实际应用

广泛应用于不同任务和领域中的图神经网络还包括网络嵌入、 图生成和时空图预测等通用任务以及其他与图相关的任务如节点聚类[24]、 链路预测[19]和图切割[25]等。 各种类型的图神经网络， 包括GCN、 GAT、 GraphSAGE 和DCNN 等，均可处理不同类型的任务。 此外， 图神经网络在推荐系统、 分子结构分析、 自然语言处理、 计算机视觉和社交网络等不同领域也得到了广泛应用。

(1)机器视觉

在机器视觉领域中， 图神经网络的应用场景包括场景图生成、 点云分类和动作识别。 其中，场景图生成模型可以利用图神经网络将图像转化为语义图[26]， 或者在已给定场景图的情况下生成逼真的图像[27]。 对于三维点云， 图神经网络可将其转化为最近邻图或上点图[28]， 并使用ConvGNN 分析其拓扑结构以进行分类和分割。在动作识别方面， 人体的关节可以形成图结构。此时， 考虑到人类关节位置的时间序列， 图神经网络被用于学习人类行动模式[29]。 除了上述在计算机视觉领域中的应用场景， 图神经网络还被广泛应用于其他领域， 如少样本图像分类[6]、 语义分割[30]、 视觉推理[31]和问答[32]等方向。

(2)自然语言处理

在自然语言处理领域， 图神经网络的应用越来越受到关注。 其中， 文本分类是最常见的一种应用， 它通过文档或单词之间的相互关系来推断出文档标签[33]。 此外， 在自然语言数据中可能包含内部的图结构， 例如句子的句法树(该树定义了句子中单词之间的句法关系)。 为了处理这一问题， 研究人员提出了句法GCN 模型[34]， 并将其应用到机器翻译任务中。 另一个应用是图-序列学习， 通过给定抽象单词的语义图， 生成具有相同含义的句子。 相关研究人员提出了一些模型， 并将其应用于图-序列学习和机器翻译任务[35]。 除此之外， 还有一个反向任务: 序列-图学习， 它可以利用句子生成语义图或知识图， 以支持知识发现过程[36]。

(3)交通预测

图神经网络在交通领域的应用非常广泛。 对于智能交通系统而言， 基础任务之一是精确地预测交通网络中的交通速度、 交通量和道路密度，这对于实现智能交通具有至关重要的意义。 研究者设计邻居子集深度神经网络来预测时空数据[37]， 该方法将深度神经网络和子集选择方法相结合， 从附近的道路中提取有用的输入。 可以通过拥塞周期模式选择适当的输入子集进行训练， 以减少输入数据维度并避免非高峰时段自由流量的人为高相关性。 另一方面， 出租车需求预测也是交通领域中的另一工业级别应用。 Wu 等提出一种深度神经网络， 该网络利用多源城市数据捕获特定的地理空间和时间依赖性， 用于城市规模的出租车需求预测[38]。 在时间依赖性方面，通过引入时间元数据， 建立了时间引导模块， 增强了时间间隔之间的相关性。

(4)推荐系统

基于图的推荐系统采用物品和用户作为节点， 通过对物品与物品、 用户与用户、 用户与物品之间的关系和内容信息进行分析， 可以产生高质量的推荐结果。 推荐系统的核心是对与物品相关联用户的重要性进行评分， 因此可以被视为一个链路预测问题。 在预测用户和物品之间的缺失链路方面， Li 等提出的神经网络是通过展开矩阵分解公式来设计的， 并通过使用所有单个观察条目进行端到端训练来学习[5]。 Solairaj 等则结合spikeNN 和情感分析生成已知评分的潜在过程，从而完成了缺失链路的预测任务[39]。

(5)化学领域

在化学领域， 图神经网络被广泛应用于研究分子的图结构， 其中节点表示原子， 边表示化学键。 分子图的节点分类、 图分类和图生成是分子学习中的三个主要任务， 这些任务被用于学习分子性质[4]， 蛋白质-配体结合亲和力[40]以及药品设计[41]。

(6)其他应用

除了以上提到的领域和任务， 图神经网络还可以应用于芯片设计[42]、 虚假新闻检测[43]、 程序验证[44]等工作。

4 讨论与总结

图神经网络具有强大的数据分析能力， 但由于图结构具备高度复杂性， 相关研究仍面临一些挑战。 为此， 笔者提出了三个未来方向， 以应对这些挑战。

(1)模型深度

深度学习中深层神经网络的架构是核心， 在处理图数据时， 需要合理采用深度学习方法。Kim 等的研究表明， 随着图卷积层数的增加，ConvGNN 的性能会急剧下降[45]。 这是由于图卷积层将相邻节点的表示程度处理得越来越接近，在理论上， 如果有无限数量的图卷积层， 所有节点的表示将会收敛到单个点， 对相关工作有负面的影响。

(2)平衡伸缩性

多数图神经网络难以适应大型图的深层架构。 这是因为当堆叠多个GCN 时， 节点的最终状态涉及其大量邻居的隐藏状态， 从而导致反向传播的高复杂性。 虽然一些方法试图通过快速采样、 分层采样和子图训练来提高模型效率， 但是它们仍然无法处理具有大规模图结构的深层架构所需的可扩展性。

(3)动态性和异构性

自然界中的图结构通常是动态和异构的。 为了更好地适应动态和异构图结构， 需要研究新的图卷积方法。 现有的图神经网络通常假设图是同质的， 并且所有节点和边缘都具有相似的特征，这在处理多类型或多模态的异构图时存在困难。因此， 需要进一步研究如何应用异构图的新方法， 以实现对动态和异构图的更高效准确的建模。

本文对图神经网络进行了全方位的概述。 将图神经网络分为两大类: 基于谱域的图神经网络和基于空域的图神经网络， 并提供了详细的分类方法。 论文还对同类别和不同类别中的方法进行了回顾、 比较和总结。 此外， 本文还介绍了图神经网络广泛的应用领域， 讨论了数据集、 开源代码等。 最后， 探讨了图神经网络三个未来发展方向， 旨在推动图神经网络更好地服务于各种实际应用场景。