智能井液压控制系统流体瞬变特性分析

熊浪，何东升，栾京生，李若岚，郑家乐

(西南石油大学机电工程学院，四川成都 610500)

0 前言

智能完井系统是近年来新型的油藏管理开发技术，采用电信号控制流量控制阀容易受到地层磁场干扰，并且井下环境恶劣，其稳定性及适用性得不到很好的保障。为了使流量控制阀长时间稳定工作，常常利用全液压控制的方式来代替电信号控制，形成了长管线液压控制体系[1]。这导致控制系统的液压管线长时间处在井下连续变化温度的环境中。而液压管线油液输送过程中，液压油的流体参数对环境温度变化十分敏感，直接影响地面打压信号向解码器系统的传输，且油液在流动过程中会因为各种原因的影响而发生水力瞬变，产生的过高或者过低的压力对管线及解码器系统造成一定破坏[2-3]。而现阶段传统管道瞬变流分析方法忽略了温度的影响，不适于井下液压管线系统的实际工况，采用这种方式务必会产生较大误差。

为探讨井下液压管线非恒温瞬变流现象，研究地面压力信号在管线内部的变化情况，作者将管道瞬变流基本方程组应用于液压控制管线，考虑温度压力变化及含气量对密度、黏度以及液压油体积模量等相关流体特性影响，结合边界条件求解得到液压管线流体末端压力随时间的变化情况，与20～100 ℃(梯度20 ℃)流体参数为定值下末端压力信号响应对比，探讨了温度梯度变化对压力信号影响；并且基于所得井下液压系统瞬变理论模型对井下长管线潜在的水锤问题进行了研究，对比分析了不同含气率及含气率一定时各个温度下水锤压力波动变化情况。

1 井下液压系统瞬变模型

1.1 基本控制方程

有压管道瞬变流遵循流体力学的三大定律，即质量守恒、动量守恒和能量守恒定律，以及相关的本构方程。在不考虑热交换的前提上，运动方程和连续性方程可全面表达瞬变流变化规律，经推导其一维瞬变流控制方程组[4]为

(1)

式中：v为平均流速，m/s；p为断面压力，Pa；g为重力加速度，m/s2；α为管道与垂直方向倾角；hf为摩阻损失，无量纲常数。

管路中波速a与流体及管壁特性相关，对于常用的金属管，可采用下式：

(2)

式中：K为流体体积弹性模量，Pa；E为管壁弹性模量，Pa；e为管壁厚度，m；ρ为流体密度，kg/m3；c1为根据管子支撑情况所确定系数。

1.2 摩阻类型

管线一维控制方程常常采用拟稳态假设，即计算稳态流动时摩阻来代替管内瞬变流动摩擦损失，但最近几年来国内外理论和实验研究表明：这种假设不能准确地预测压力波衰减和波形畸变过程[5]。故为提高模拟精度，采用国外最新研究一维非常规瞬变流模型，即Vitkovsky模型[6]，该模型由稳态摩阻损失和非稳态摩阻损失组成，弥补了Brounone计算非恒定摩阻模型的不足。公式表征为

(3)

式中：hfs为稳态摩阻，其中f为稳态流动下管道摩擦因数，与流动状态相关；kv=0.03，为Vitkovsky衰减系数；SGN(v)表征流体方向，若v≥0则SGN(v)=1，若v<0则SGN(v)=-1。

1.3 特征线法

特征线法(MOC)是瞬变流计算常用的一种方法，可以将瞬变流控制方程组转换成特殊的常微分方程，然后求得便于计算机编程计算的有限差分方程。此处忽略重力的影响，采用简化特征线法得到特殊全微分组如下：

(4)

由于摩阻项不能直接求解，需将方程组转换为有限差分形式，所以首先将管道等分为n段，每段长Δx，每个单元的时间步长为Δt，但是Δt和Δx必须满足CFL条件，即：

(5)

节点记为(xi,tn)，构造如图1所示的差分网格。

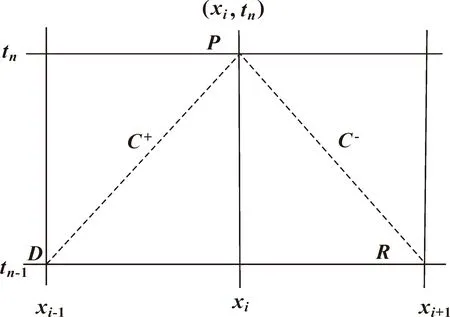
图1 差分网格

式(5)分别沿着正负特征线DP和PR方向积分得：

(6)

对于拟稳态中的摩阻项常用显示近似、线性隐式近似、ε近似以及非线性隐式近似[7]。充分考虑精度要求及避免反复迭代，故选用工程上常用的线性隐式近似：

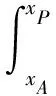
(7)

最后，利用特征线差分网格表示为

(8)

(9)

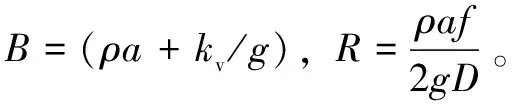
2 流体参数影响因素分析

2.1 温度对流体参数影响分析

温度对液压油的各个流体参数存在显著影响，井下各处储层温度各不相同，导致流体流经井下管线时，内部流体参数发生变化，从而引起压力流量发生改变，因此必须要了解储层温度与井深之间的关系，才能计算流体参数在管线内部发生的变化。由于不同地貌特征及温度气候各处地温梯度关系各不相同，故根据杨绪充[8]对东营地区地温与深度的研究数据，得到油井各处温度和井深的线性关系，并将得到数据进行线性拟合，如图2所示。

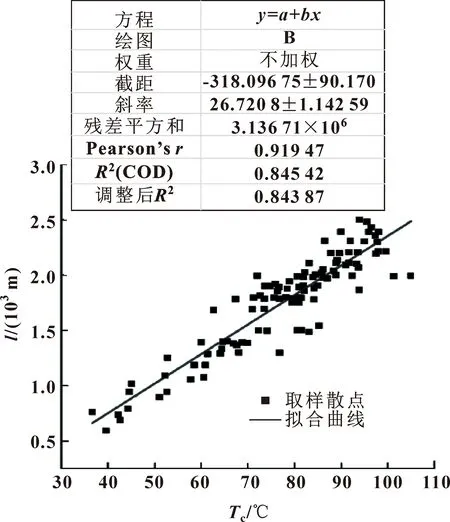
图2 东营凹陷地区温度梯度随井深变化

图2中储层温度与井深的线性关系表示为

Tc=T0+ζ·l

(10)

式中：Tc为储层温度，℃；T0为初始温度，℃；ζ为地温梯度系数，℃/m。

2.1.1 黏温-黏压特性

井下液压管线处于一个温度持续变化的复杂环境中，管线中流体的黏度受温度的影响较大，工程中常用的Roelands黏温-黏压关系式[9]为

η=η0exp{(9.67+lnη0)[(1+5.1×10-9p)Z·

(11)

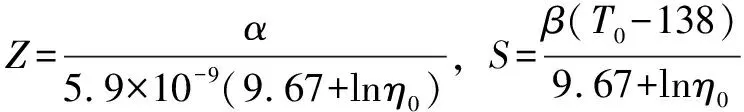
式中：η0为环境黏度；α为黏压系数，取2.2×10-8m2/N；β为黏温系数，取0.040 2；T0为环境温度，取313.5 K。

2.1.2 密压-密温特性

通常而言液压油的密度随压力温度变化很小，几乎可忽略不计，被认为是不可压缩流体。但在井下高温高压的环境下，液压油内部性质会发生一定的变化，必须考虑温度压力对于密度的影响，进行校正。液压油密度是温度及压力的函数，在实际工程及文献中经常用经验公式[10]来计算温度、压力与液压油密度的关系：

ρ=

(12)

2.1.3 温度压力对体积模量的影响

温度、压力不仅影响液压油的黏度和密度，还会影响其体积模量K：

(13)

式中：A、B1-B4表示液压油特性系数。32号液压油特性系数如表1所示。

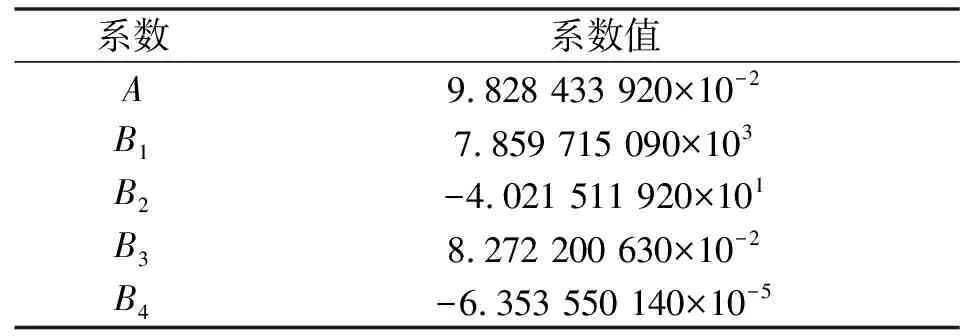
表1 32号液压油特性系数

2.2 考虑含气量对液压油流体参数影响

近年来，含气瞬变流一直是研究的热点。井下管线内在打压过程中，不可避免会掺杂少许气体，对于管线内液压油中的空气，一般以两种形式存在：溶解于油液中和未溶解于油液中。对于油液的流体参数，溶解于油液中的空气是没有影响的，故仅考虑未溶解于油液的空气的影响。通常使用综合密度、综合黏度及综合体积模量分别表示[11-12]。

(14)

ηzong=η(1+0.015Cu)exp[αp-β(T-T0)]

(15)

(16)

式中：ρaSTP为标准状态时空气密度，取1.293 kg/m3；ρlSTP为纯油密度，取872 kg/m3；Cu为含气量；pSTP为标准状态压力，取0.101 315 MPa；psat为饱和状态时压力，取0.2 MPa；p为油液压力；T为油液温度；k为空气比热，取1.4；η为油液标准黏度；α为黏压系数，取2.2×10-8m2/N；β为黏温系数，取0.040 2 K-1；T0为液压油初始温度，取288.6 K。

3 案例计算结果及分析

3.1 参数敏感性分析

为确定管线的管径、壁厚等因素影响，完成井下管线优化选型，为井下管线含气瞬变流模型确定初始参数，结合管道子模型选取原则[13]，利用AMESim搭建如图3所示的井下液压长管线计算模型并结合如图4所示地面打压信号进行参数敏感性分析。

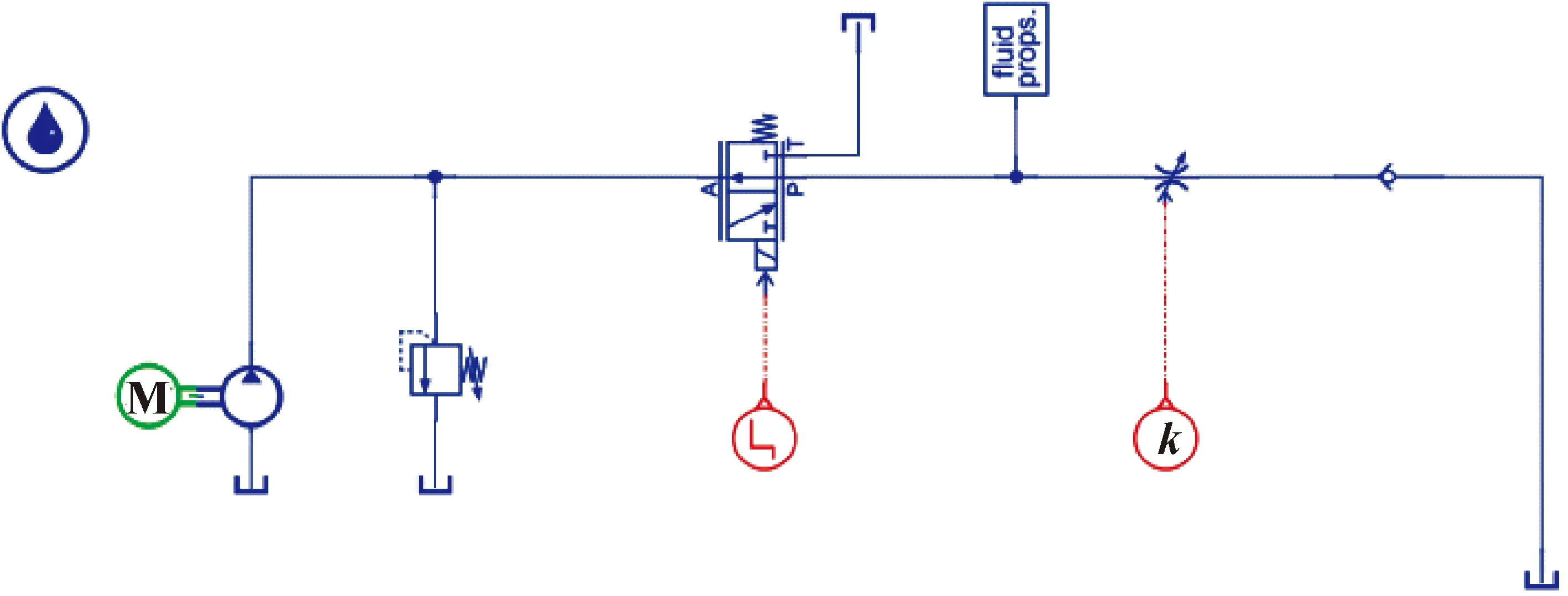
图3 井下管线工作模型

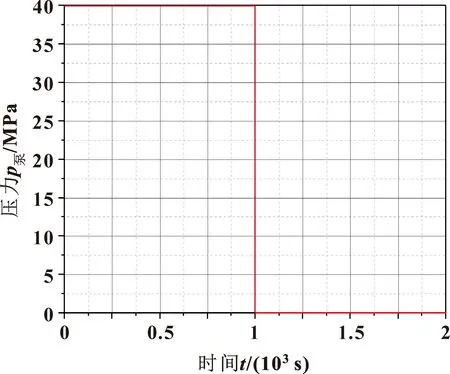
图4 控制平台压力信号

3.1.1 管径大小的影响

以管径作为研究对象，利用AMESim批处理功能，分析管径d为2～7 mm(梯度1 mm)时管线末端压力变化如图5所示。

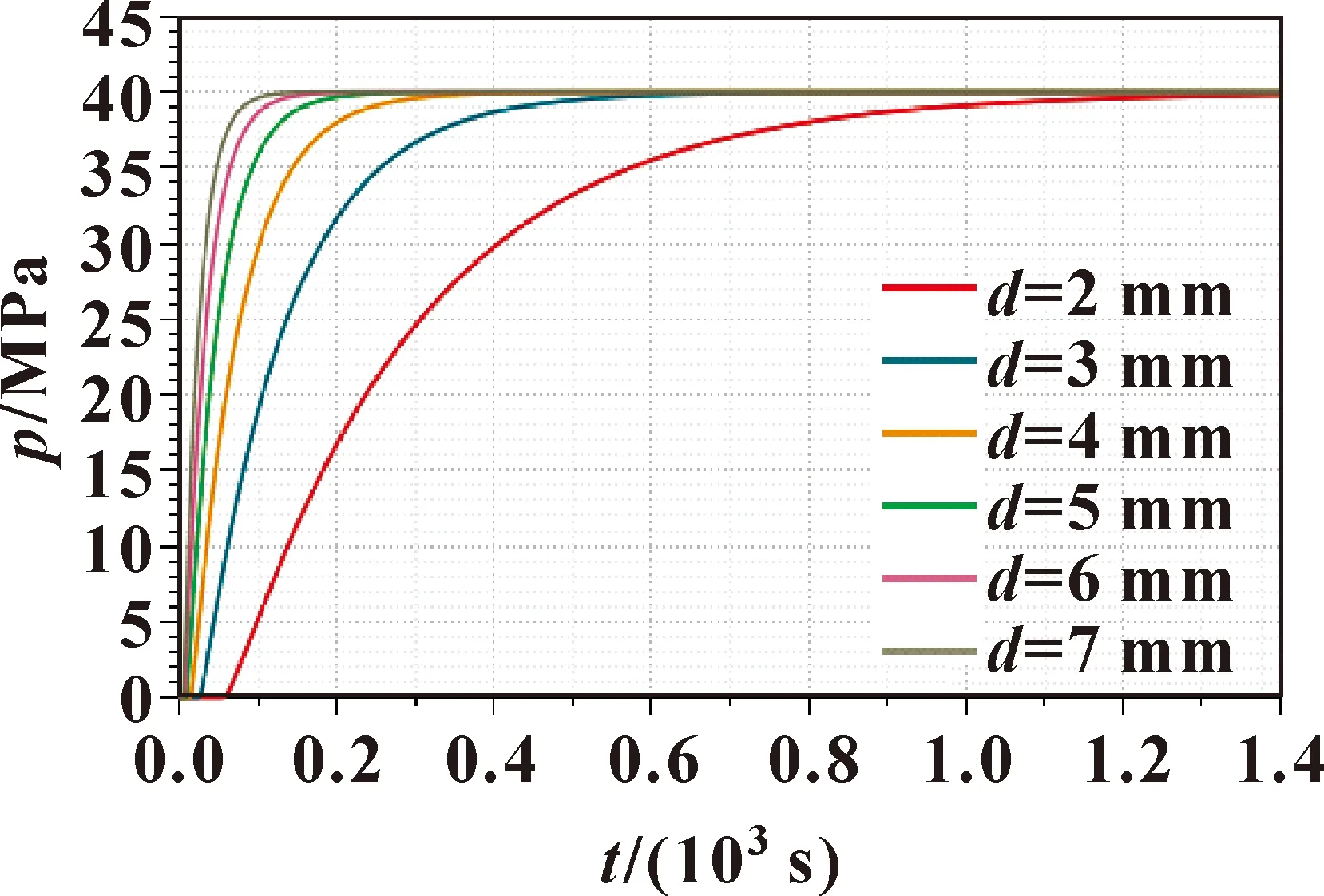
图5 管线末端压力曲线(变化管径)

由图5可知：在压力不变的情况下，管径越大管线末端压力信号传递越快，压力到达稳定值所需要时间越短。但是由流量变化曲线(图6)可知，管径越大末端造成的波动越大。因此结合实际工程情况，选择管径为3.048 mm。

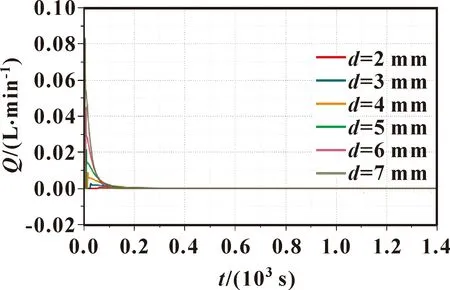
图6 管线内流量曲线

3.1.2 管线壁厚的影响

同理分析壁厚对末端压力的影响，将管线壁厚t设置为1～4 mm(梯度1 mm)，运行仿真，得到管线末端压力变化情况如图7—8所示。

图7 管线末端压力曲线(变化壁厚)

由图7和图8可知：随着壁厚的增加，管线末端压力响应越迅速，但总体上来看，壁厚的增加对管道末端压力影响不大，故可忽略管壁的影响。结合实际工程，在现场应用的管线外径为6.35 mm，内径为3.048 mm，壁厚为1.651 mm，材料为316L不锈钢，弹性模量为210 GPa。

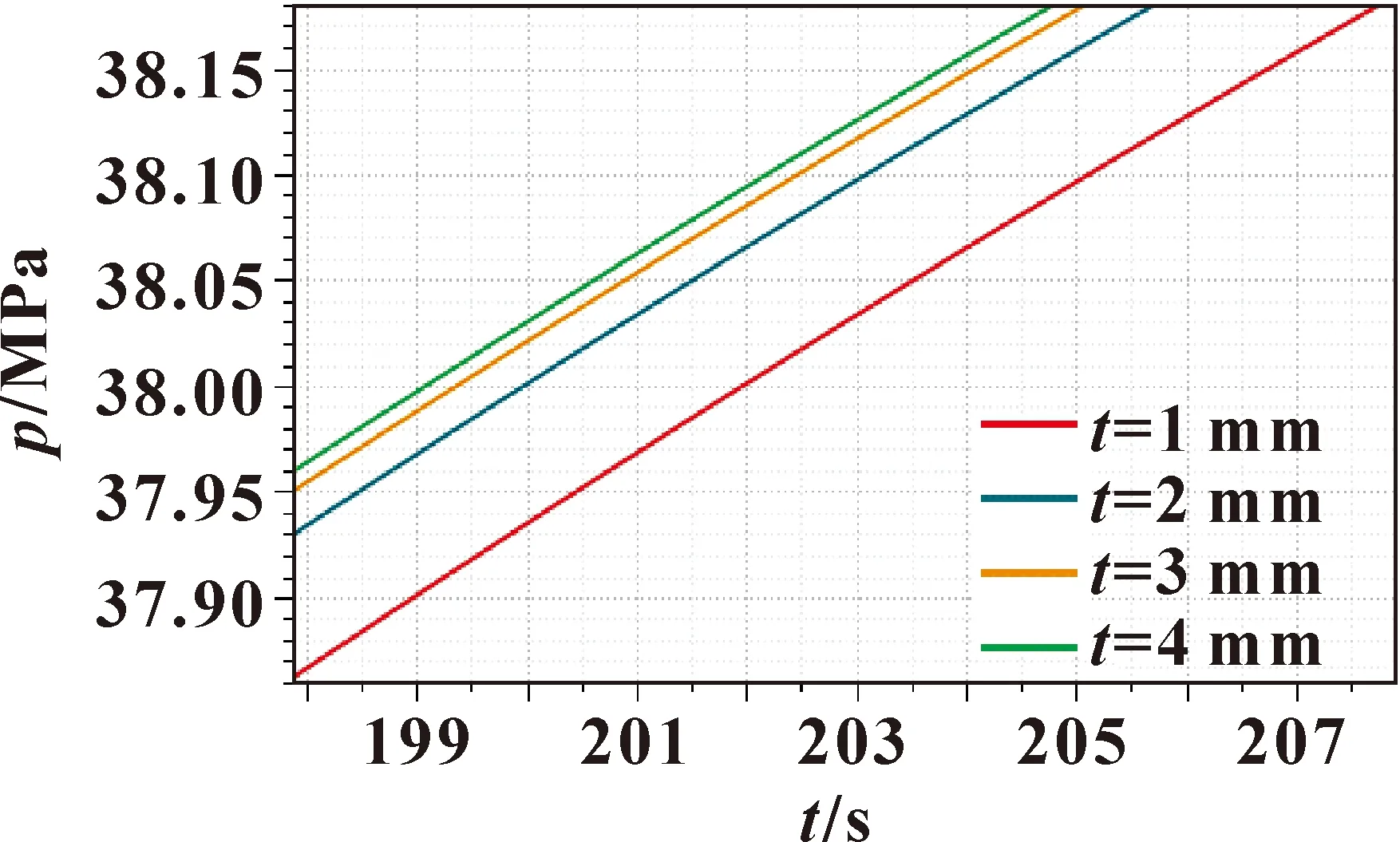
图8 管线末端压力曲线详图

综上所述可得，井下液压管线瞬变流仿真参数如表2所示。

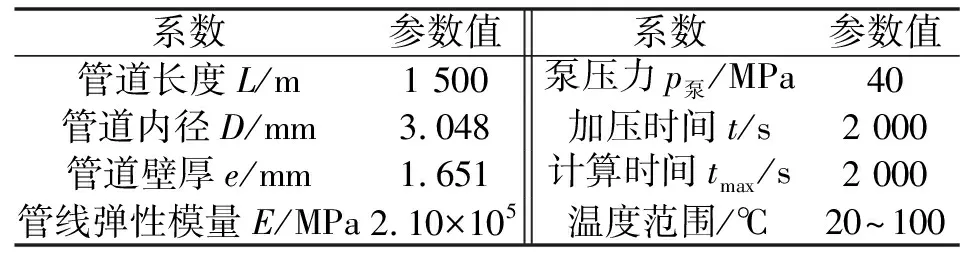
表2 仿真参数

3.2 数值计算模型

井下液压长管线属于一维管道模型范畴，基本控制方程由连续性方程与动量方程组成。结合流体参数影响因素分析，总结出如下形式瞬变流的内部节点流体参数数值求解模型：

(17)

(18)

(19)

通常情况下，瞬变分析总是从稳态分析开始的，假设该时刻t=0，利用地温梯度计算出各个节点的温度值，然后利用式(8)、公式(17)—(19)计算出各个节点的值，然后得到v、p的初始值；在t=Δt时刻，基于初始值和以求出各节点的流体参数值，通过式(8)、公式(17)—(19)计算得到各节点上的v、p值。以此类推，则可计算得到在不同时刻t=2Δt，t=3Δt，…，t=NΔt的v、p值，通过MATLAB进行编程的计算框图如图9所示。

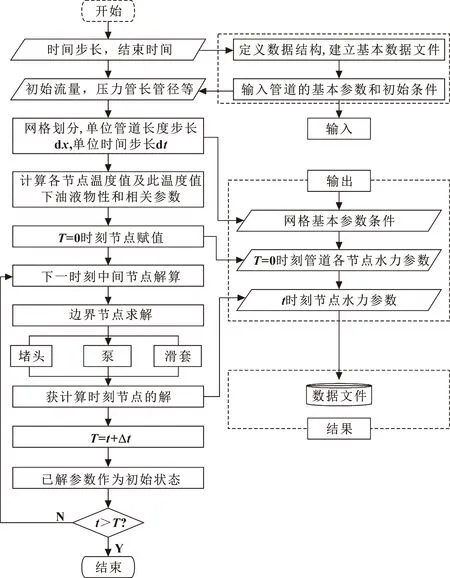
图9 程序框图

3.3 数值结果分析

3.3.1 管线末端值响应问题

要完全得到管线各个位置的压力、流量的分布情况，不仅需要上述推导过程，还需要确定管线的初始流动状态以及管线两端的初始状况，即管线的边界条件。针对不同的问题，边界条件的取法一般有以下两种：一是管线系统边界节点处的压力或流量为常数；二是结合相容方程确定边界处节点的平衡条件。作者结合地面液压控制平台给解码器施加压力信号的情况可知，当压力信号未达到解码器之前，管线末端阀门可视为关闭状态。因此对于末端压力响应可确定的初始条件和边界条件：

(20)

当含气率一定时，定温度设置流体参数条件下与考虑地温梯度条件下末端压力值的变化情况如图10所示。可知：考虑温度梯度和定参数分析管线内瞬变流，其管线末端压力达到稳定值存在较大差异，并且温度越高，流体参数及摩阻值越小，末端压力响应越快；温度梯度对末端压力信号影响介于定参数60～80 ℃影响之间；且根据计算结果，管线末端达到泵压力大小的95%(38 MPa)大概需要200 s，达到100%泵压力大小需要796.12 s，管线末端压力响应具有一定时长延迟。由于井下流量控制阀各个开度动作需要泵压达到指定压力才进行相应动作，所以这个延迟时间是作者研究重点，可为井下流量控制阀的开度动作提供参考。

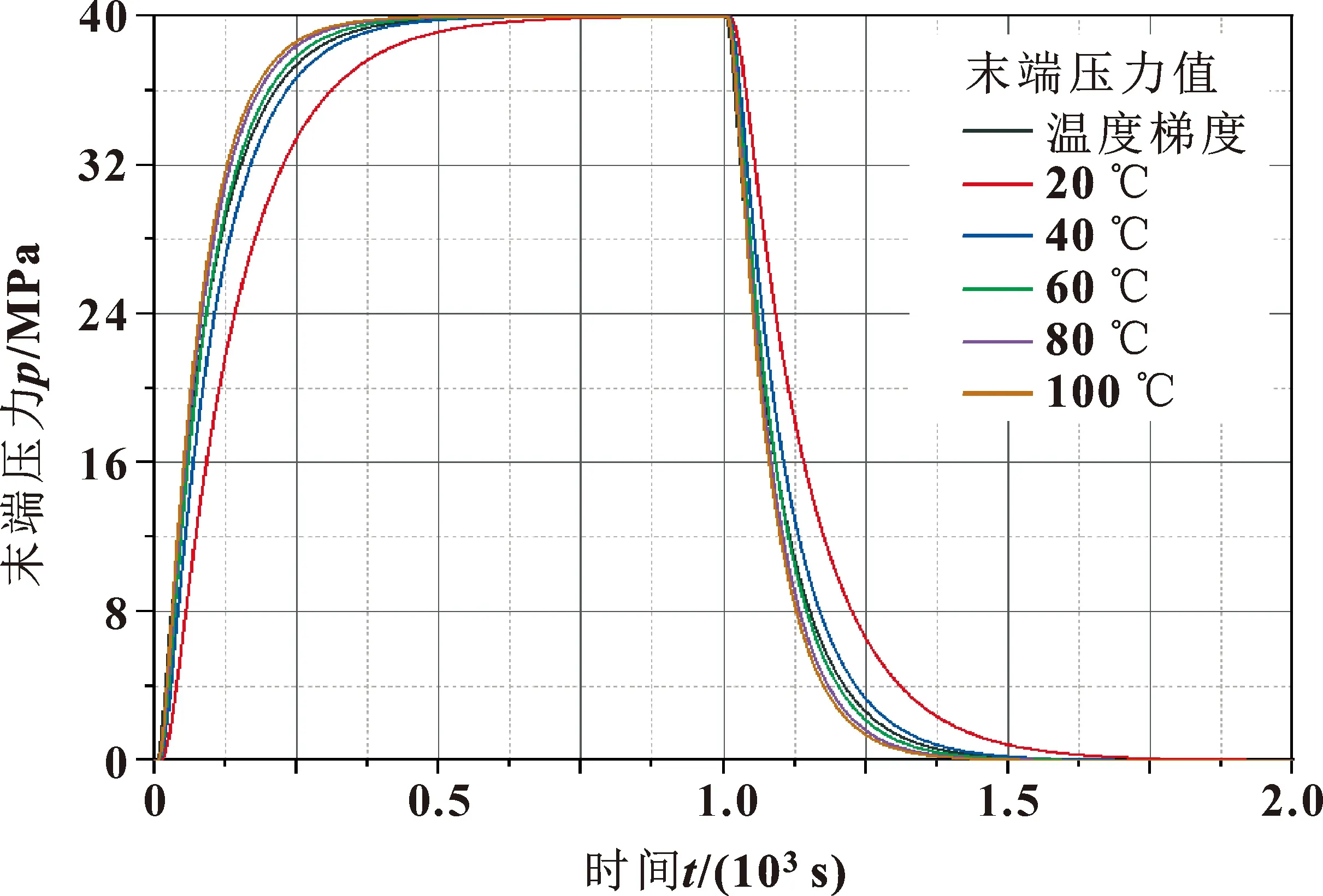
图10 管线末端压力信号的变化情况

管线内空气含量直接会影响管线内流体参数，从而影响管线内流体压力和流量变化，但是液压油流体性质决定含气量不会太高，故此分析含气量Cu为0、0.5%、1%时管线末端压力的变化情况，如图11所示。可知：含气量对管线末端的压力存在影响，含气量越高，则管线末端达到稳定压力的时间越长，但是油液中含气率过小而导致对末端压力响应影响不是特别明显。

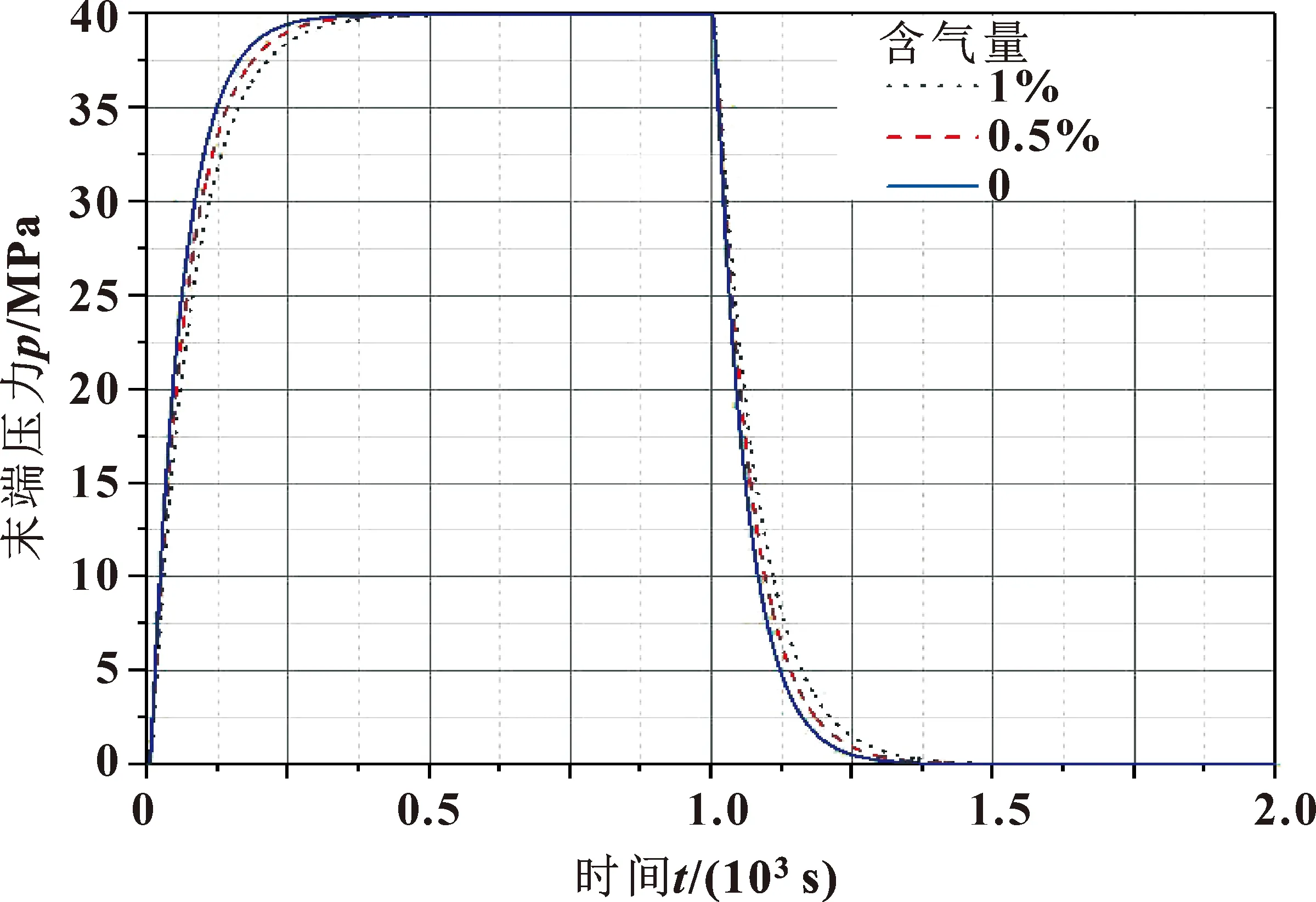
图11 不同含气量等线末端压力对比

3.3.2 水锤问题

在压力管道系统中水锤问题是经常会遇到的现象，通常水锤瞬间造成的高压，甚至有可能是管道可承受压力的几十倍或者几百倍，对压力管道系统造成严重破坏，故对解码器达到最大压力后可能引起的水锤问题展开研究。管线水锤问题对应的物理模型的控制方程同式(8)、公式(17)—(19)，而水锤问题对应的边界条件分析如下。

管线上游边界：

当解码器开启并稳定运行时，出口末端可视为节流阀，以孔口出流的方式来确定压力与流量的关系，由此可知管道下游边界[14]：

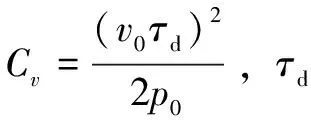
与传统水锤问题不同的是，井下管线产生的水锤会受到温度与含气率的影响，故对井下管线受温度与含气率影响分别展开研究。不同温度下数值模拟结果如图12所示。

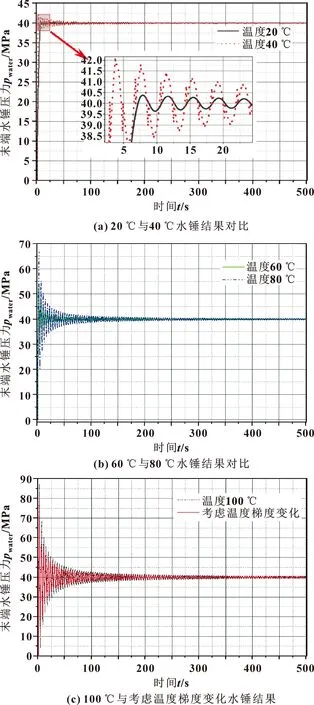
图12 不同温度下水锤仿真结果

由图12可知：温度变化对于末端水锤影响十分显著，随着温度的升高，末端水锤压力值越大，水锤变化幅度也越大，温度20 ℃时，水锤峰值为42.15 MPa，而温度为100 ℃，水锤峰值为87.26 MPa。这是由于流体黏度、密度及体积模量随温度升高而减小，从而导致摩阻系数f、特征阻抗B等相关系数减小，末端节点水锤幅值随时间的损耗降低。并且考虑地温梯度变化水锤现象与温度100 ℃水锤变化情况大致相同，但各时间段水锤幅值均小于定参数温度100 ℃，最大水锤幅值为79.92 MPa，故在管线末端材料的选用，管线设计中需考虑潜在水锤危害对解码器系统造成的影响。

同理分析含气量Cu为0、0.5%、1%时管线末端水锤的变化情况，如图13—14所示。

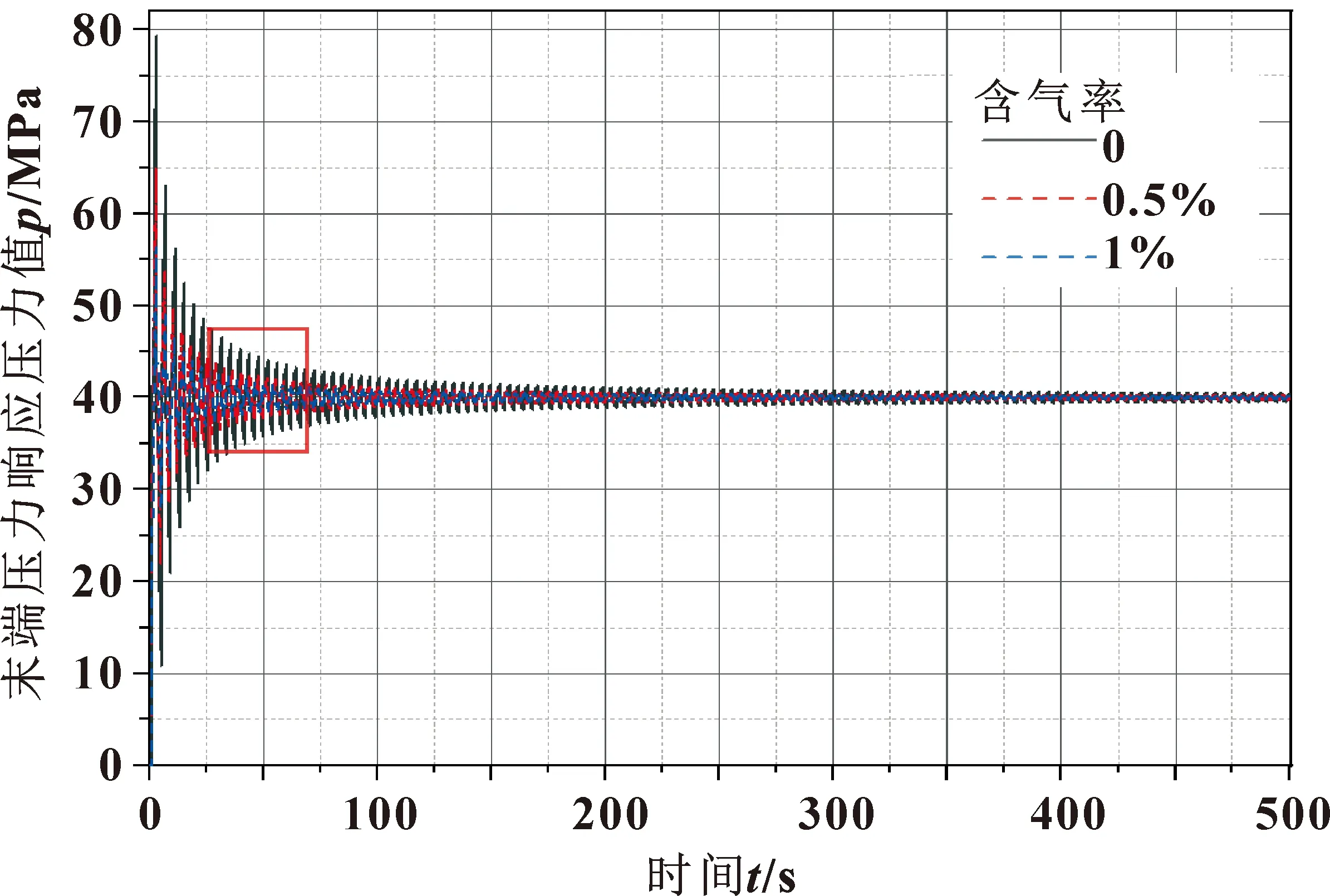
图13 不同含气率下末端水锤结果对比

由图13—14可知：随着含气率的增大，管线末端水锤压力峰值在减小，当含气率为0时，管线末端压力峰值为79.92 MPa；而含气率为1%时，管线末端压力峰值减小到了57.10 MPa；同时由图14可以看出，含气率越小，水锤周期越短，压力波动时间越长且压力峰值在尖点处越尖锐。

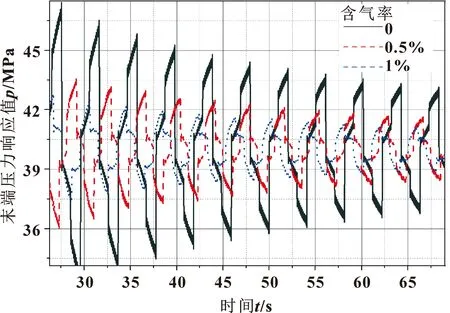
图14 不同含气率下末端水锤结果对比详图

4 结论

(1)建立非等温系统管线含气瞬变流模型，利用特征线法求解得到管线的数值解模型，在编程过程中加入了温度压力梯度变化及含气率对液压油密度、黏度及体积模量等因素影响，为小管径、非恒温含气瞬变流问题研究提供了一种思路。

(2)通过对井下管线模型进行参数敏感性分析，发现管线管径、空气含量对管线压力及流量变化影响较大，管壁厚度的影响可忽略不计。且对于管线末端压力响应来说，管径越大，压力信号响应速度越快，但是末端流量波动越大。结合工程实际选取管线管径3.048 mm，管壁厚度1.651 mm。流体参数对含气量变化较为敏感，但对于末端压力作用效果不明显，而对于潜在管线水锤影响尤为突出，含气率越小水锤峰值越大，水锤周期越短，压力波动时间越长且压力峰值在尖点处越尖锐

(3)智能井系统管线末端能够接收到来自地面的压力信号，但是会受到温度压力梯度变化的影响。根据计算结果，考虑温度梯度及含气量与定参数条件管线末端压力值差异较大，从20～100 ℃定参数末端压力值看，温度越大，末端压力响应越快，考虑温度梯度及含气量达到泵压力的95%需要时间200 s，达到100%泵压力需要796.12 s，因此可以看出管线末端响应存在较长时间的延迟，仿真结果可为流量控制阀开度动作提供参考；而温度对于水锤影响更为显著，温度越高，水锤峰值及变化幅度越大；考虑地温梯度的水锤现象，水锤幅值为79.92 MPa，故在管线设计中，需要消除潜在水锤危害对解码器系统造成的影响。