基于模糊RBF的液压压裂泵同步研究

戚伟，杨波，晁宇

(新疆大学机械工程学院，新疆乌鲁木齐 830017)

0 前言

随着国内的一些老旧油田资源的陆续枯竭，压裂增产作业需求迅速增加，同时页岩气等非常规化石能源的开采也成为包括我国在内的许多国家战略选择。而压裂车作为压裂核心装备，开始被用于常规油气田的压裂增产和页岩气等非常规化石能源的压裂开采。而压裂泵是压裂车在压裂施工时的重要组成部分。压裂车通过所搭载的压裂泵，将高压、大排量的压裂液通过井口压入地层产生地层裂缝，然后将支撑剂挤入裂缝，进而加速油气资源的渗透。其中压裂泵在工作时，液压缸的同步性对压裂效率和系统脉动有很大的影响。随着压裂技术的发展，对其自动化、智能化控制应用在设备的要求也不断提升。

近些年来国内外研究人员针对液压系统同步问题，根据不同场景和不同要求给出了不同的控制策略。例如，2005 年，WIENS等[1]设计了一款分流阀，分流比例可以随着阀芯转动角度不同而不同，该阀提高了同步精度，减少了能量损耗。2007年燕山大学的赵静一等[2]对分流阀的结构进行了改进，利用轴向缝隙式可变节流口直接调节同步阀流量，经试验验证，利用改进的分流阀进行液压同步控制同步精度得到极大改善。2010年燕山大学的赵瑜[3]针对变位机双马达液压同步控制问题，基于模糊控制理论和神经元控制理论，设计了模糊滑模变结构控制器和神经元 PID 控制器，实验结果表明：两种控制器都可以使液压同步系统控制精度得到提升，鲁棒性变强，但神经元 PID控制精度略胜一筹。2016年重庆大学的于今[4]利用模型参考自适应的前馈补偿控制策略对模锻液压机液压同步系统进行同步控制，试验结果表明：该控制策略在系统存在大偏载差异的情况下可以很好地自动纠正偏差，与传统PID控制相比具有更高的控制精度和响应速度，并且对不同的工况适应性较强。2019年山东建筑大学的李洪龙、逄波[5]针对双缸四柱液压机位移同步的功能要求，采用分数阶PID控制策略进行液压缸位置同步控制，实验结果表明：采用分数阶PID控制策略对双缸四柱液压机位置同步进行控制，满足了工作中位移同步控制的要求并且其稳定性更好、精度高和鲁棒性更强。2020年燕山大学的贾鑫龙[6]利用模糊PID控制算法对16 000 t 海上浮托安装平台进行液压同步控制，仿真结果表明：同步性较好，达到期望要求。

以上可见，目前液压缸同步策略，多是从流量控制元件、流量补偿元件以及一些PID或其他改进算法改善控制效果。以上控制策略虽能达到液压缸的同步，但是控制精度低，同步误差较大，容易受到外界扰动影响，系统稳定性差。根据以上传统控制存在的问题，通过伺服阀控液压缸数学模型设计了位置跟踪器和同步控制器，构造出基于模糊RBF神经网络+交叉耦合控制策略，该控制策略在给定模糊控制规则的基础上融入了收敛速度快、抗干扰能力强的RBF神经网络。仿真结果表明：该控制策略响应速度快、控制精度高、抗干扰能力强，对液压压裂泵同步系统的实际应用提供了参考。

1 系统建模

1.1 位移传感器建模

放大器的作用是把电压误差信号转化为阀的电流信号进而控制阀的开口大小。其偏差电压信号为

Ue=Ur-Uf

(1)

式中：Ur为给定电压信号值，V；Uf为反馈电压信号值，V；Ue为偏差电压信号值，V。

放大器数学表达式为

i=KaU

(2)

式中：i为放大器输出电流，A；U为放大器输入电压，V；Ka为增益系数，V/A。

位移数学表达式为

(3)

传递函数为

(4)

式中：X为位移传感器检测到液压缸输出位移，m；U为位置传感器输入电压，V；Kf为增益系数，V/m。

1.2 伺服阀建模

阀控缸原理示意如图1所示，用经典控制理论的分析方法对其进行线性分析。

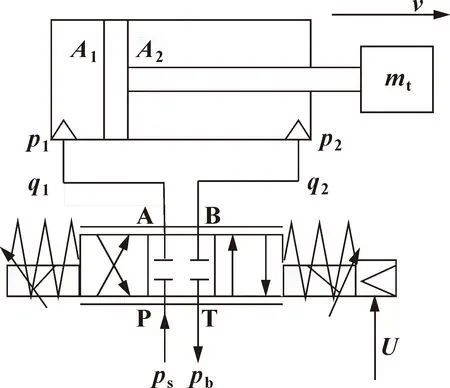
图1 阀控缸原理

(1)伺服阀线性化流量方程

阀控缸伺服位置系统动态分析是在零位工作条件下进行的，其增量与变量相等，所以用变量本身表示它们从初始条件下的变化量，即流量方程为

qL=KqXv-KcpL

(5)

式中：qL为伺服阀的输出流量，L/s；pL为负载压力，Pa；Kq为流量增益，m2/s；Kc为压力系数，m5/(s·N)；Xv为阀芯位移量，m。

(2)阀控缸的流量连续性方程

(6)

式中：Ctp=Cip+Cep/2为总的泄漏系数，反映液压缸泄漏对负载流量的影响；Ap=1/2(A1+A2)为活塞的平均面积；V1=V2=Vt/2，Vt为压液缸的总容积；A1、A2分别为液压缸无杆和有杆腔有效面积，m2；V1、V2分别为液压缸进回油腔的容积，m3；Cip、Cep分别为液压缸的内外泄漏系数，m3/(s·Pa)。

(3)缸与负载的动力学方程

液压动力元件的动态特性与负载特性有关[7]。在这里忽略缸与活塞之间的摩擦阻力等非线性因素情况下，则动力学方程为

(7)

由A2=nA1得，

(8)

式中：mt为总质量，kg；K为负载弹性刚度，N/m；Bp为黏性阻尼系数，N·s/m；FL为负载力，N。

(4)模型求解

联立方程式(5)(6)(8)进行拉氏变换得阀芯位移与液压缸位移之间的传递函数为

XP(s)=

(9)

将式(9)传递函数简化为

(10)

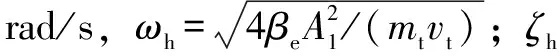
所以开环传递函数为

(11)

式中：ωv为伺服阀固有频率；ζv为伺服阀阻尼比；kafv为kakfkv/A1，kv为伺服阀增益。

2 控制器设计

模糊控制的优点是利用编写的控制规则进行控制，对被控模型没有过高的要求；缺点是受外界影响较大，抗干扰能力较弱，精度不高。RBF神经网络结构简单、收敛速度快、抗干扰能力强，克服局部极小值问题，网络连接权值与输出呈线性关系[9]。但RBF神经网络在控制过程中没有控制规则的参与，同时对被控模型要求较高。通过分析比较两者的优缺点，将两者优点结合起来，利用RBF 神经网络整定模糊控制的隶属度函数，也利用控制规则进行学习，可以极大地改善系统性能[10]。控制器原理如图2所示。

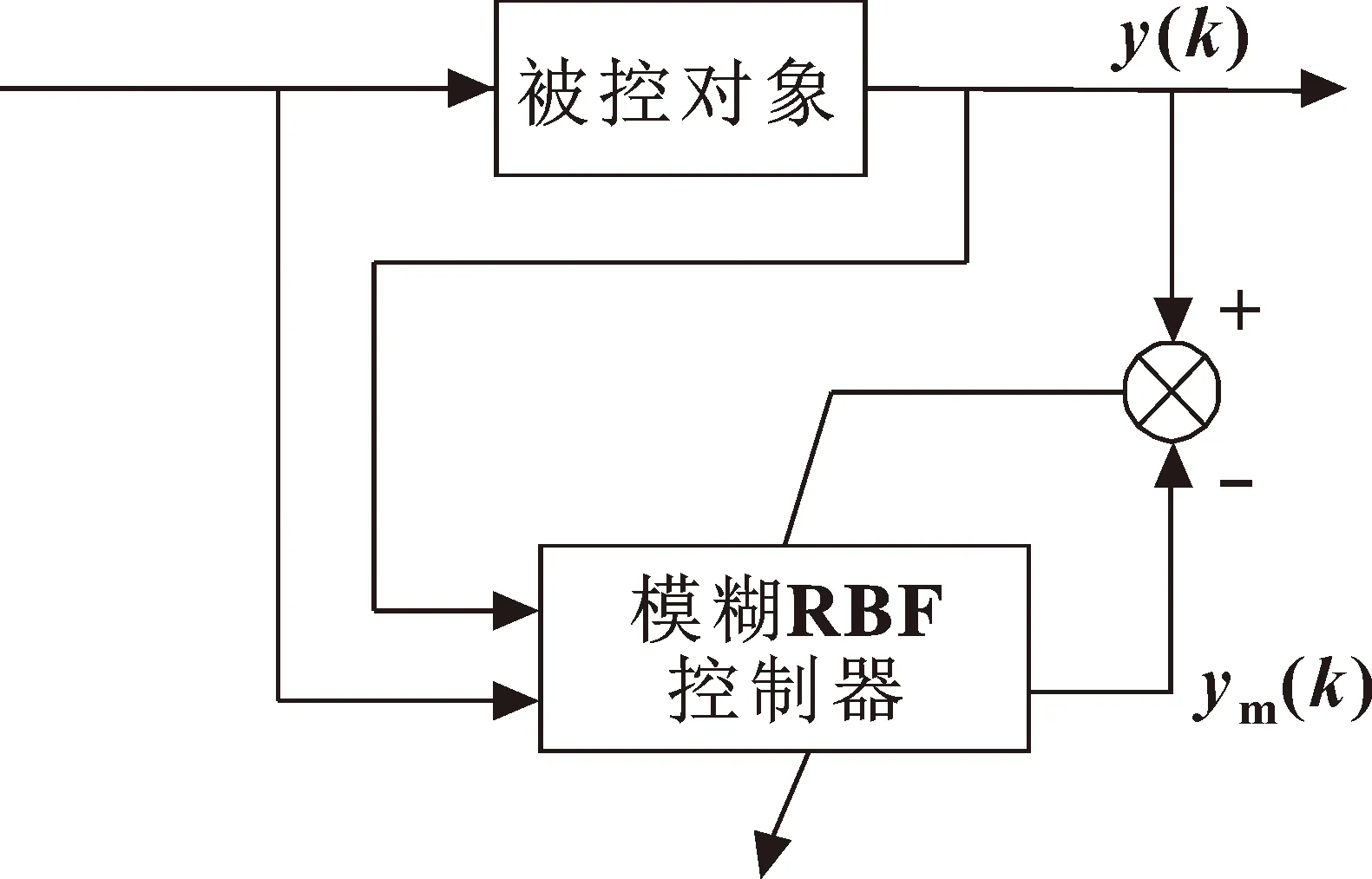
图2 模糊RBF控制原理

2.1 模糊RBF结构

模糊RBF结构如图3所示。x代表神经元输入，即阀控缸伺服系统给定位移输入，y代表阀控缸伺服系统位移实际输出，ym为阀控缸伺服系统经过模糊RBF神经网络控制的输出值。

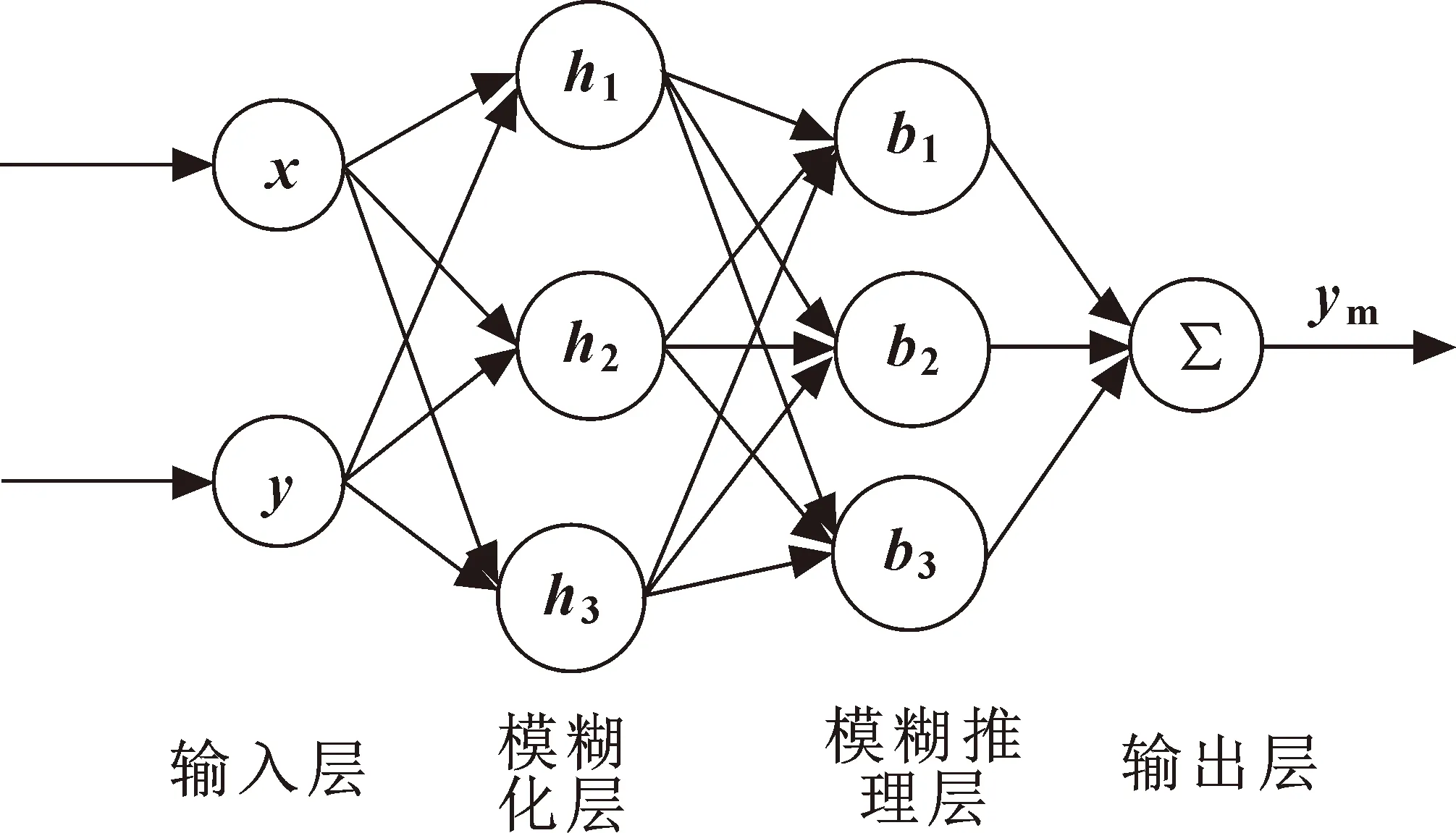
图3 模糊RBF结构原理

(1)输入层

输入层的各个节点与输入量的各个分量连接，对该层的每个节点i的输入，输出表示为f1(i)=xi。

(2)模糊化层

采用高斯型函数作为隶属函数，即表示为f2

(12)

(13)

式中：i=1，2；j=1，2，3，…，n；bij、cij分别为隶属函数的宽度值与中心值。

(3)模糊推理层

完成模糊规则的匹配，实现各节点间的模糊运算。其输出表达式为f3

(14)

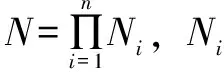
建立模糊规则如表1所示，按照E与ΔE模糊化的结果，结合模糊规则表和隶属度函数在MATLAB中编写出49条模糊规则。

表1 模糊规则

模糊规则确定后，比例系数Kp、积分系数Ki、微分系数Kd的控制曲面如图4所示。

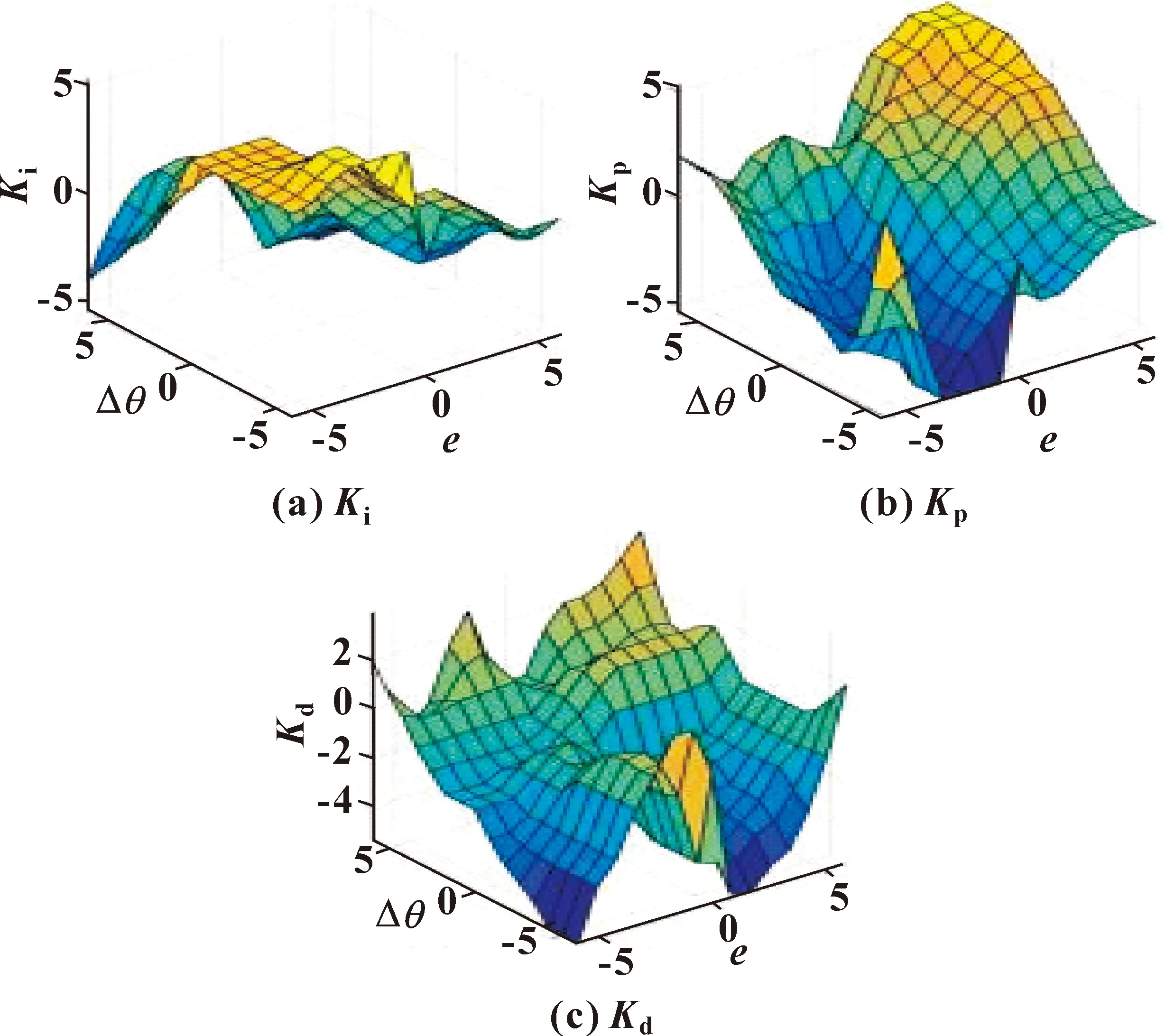
图4 控制曲面

(4)输出层

实现规则间的推理，表示为f4

(15)

式中：ω为连接权矩阵。

2.2 模糊RBF的更新公式

利用梯度下降法对参数进行更新[11]，其y、ym为阀控缸系统的实际输出值和网络的输出值，定义网络的损失函数为

e(k)=y(k)-ym(k)

(16)

(17)

迭代更新算法如下：

ω(k)=ω(k-1)+Δω(k)+α[ω(k-1)-

ω(k-2)]

(18)

η[y(k)-ym(k)]f3

(19)

bj(k)=bj(k-1)+Δbj+α[bj(k-1)-bj(k-2)]

(20)

(21)

cij(k)=cij(k-1)+Δcij(k)+α[cij(k-1)-

cij(k-2)]

(22)

(23)

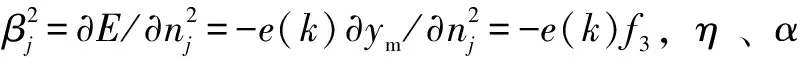
3 同步控制策略

液压系统同步控制策略有主从同步、等同同步、交叉耦合同步控制[12]。主从同步以一个液压缸的输出信号作为主输出信号，同时将该主输出信号作为其他液压缸的输入信号以达到同步控制的效果，这种控制策略会导致从动缸有累计误差，并且从动缸动作始终滞后于主动缸[13]。等同控制是将每个液压缸各自形成一个控制单元，由各自控制系统控制，各个支路之间分别独立，互不干扰，所以各支路之间耦合作用小[14]，同步误差受各液压缸的运动参数影响。“交叉耦合”控制使两个被控对象之间产生相互作用，把控制结果经过耦合控制器反馈到前面各自的控制器中，完成实时同步控制，其控制效果优于其他两种控制策略[15]。基于以上分析，选用同步精度高的交叉耦合同步控制策略。控制原理如图5所示。

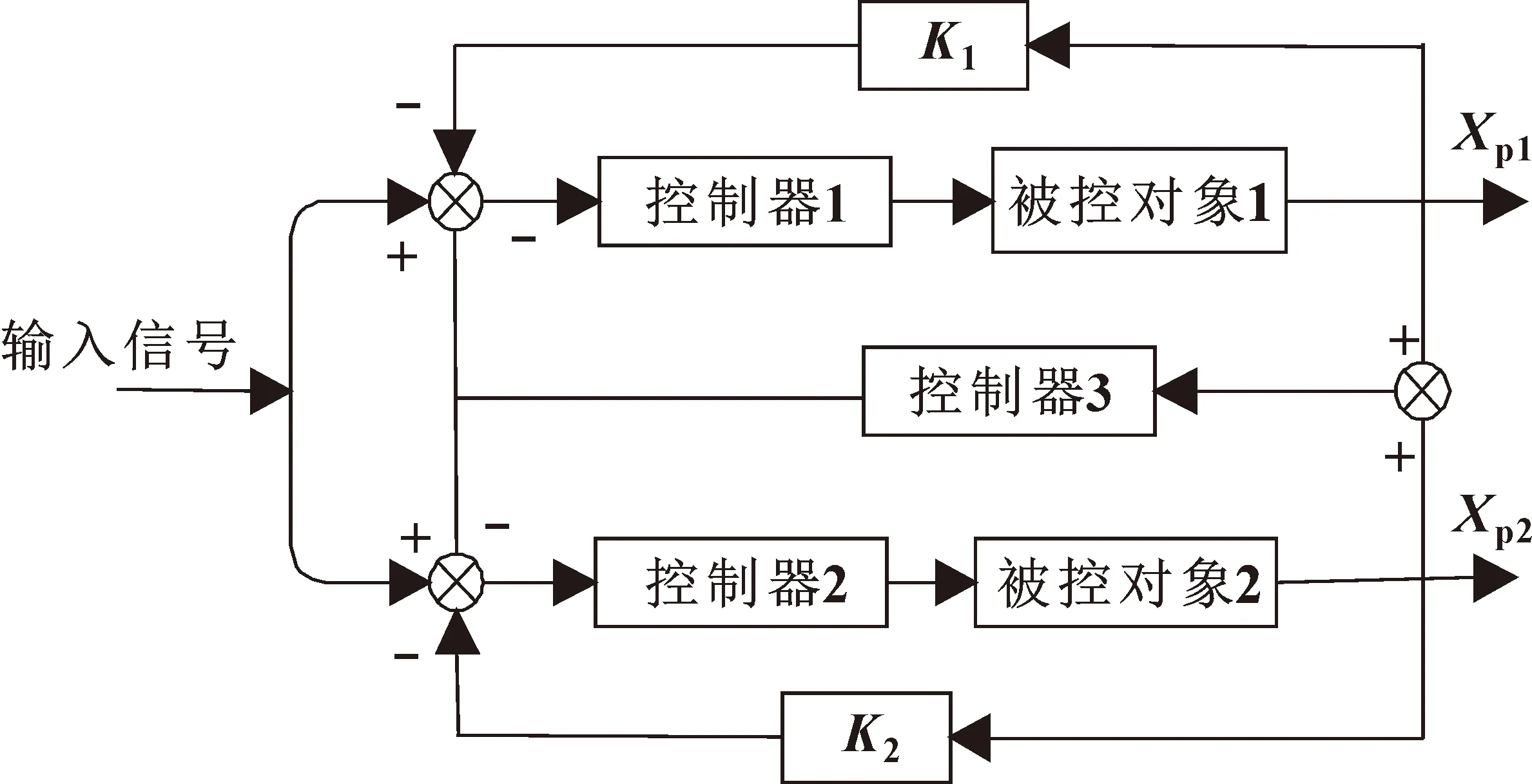
图5 交叉耦合控制原理

4 仿真结果分析

根据以上推出的数学模型，在MATLAB/Simulink软件中进行模型搭建，利用s函数编写运行程序，分别研究PID、模糊PID、模糊RBF三种不同控制策略下，液压缸的同步控制效果。仿真模型参数设置如表2所示。

表2 模型参数

4.1 阀控缸控制策略验证

系统结构如图6所示，输入阶跃信号目标值为0.50 m，控制系统响应曲线如图7所示，PID控制系统在1.9 s达到稳定状态；模糊PID控制系统1.1 s达到稳定状态；模糊RBF在0.7 s达到稳定状态。模糊RBF相比PID控制响应时间缩短63.2%，与模糊PID相比响应时间缩短36%。可以看出，模糊RBF控制系统响应时间短响应速度最快。

图6 Simulink系统结构

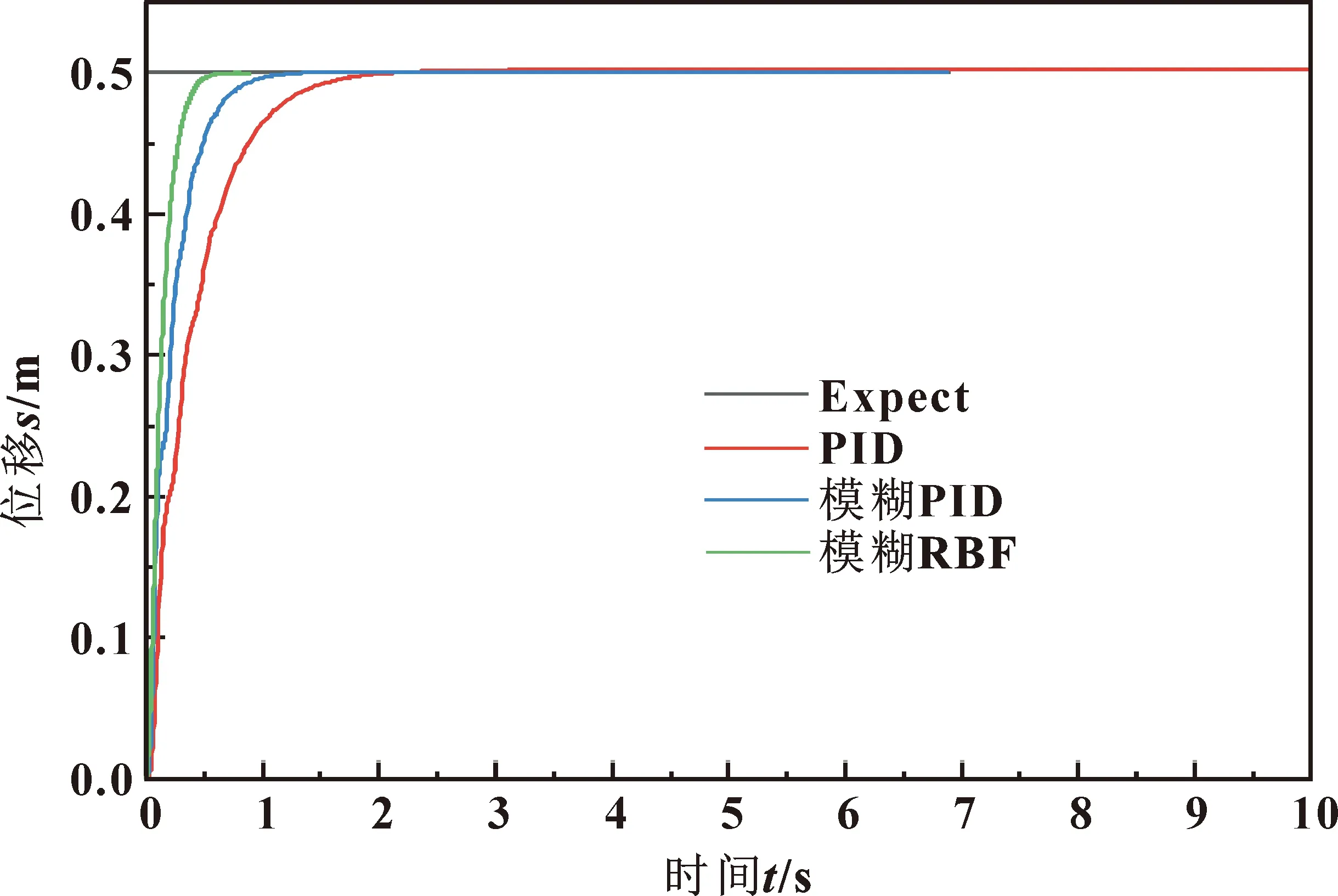
图7 系统响应曲线

误差响应曲线如图8所示，传统PID控制跟踪误差为1.6 mm；模糊PID控制误差为0.7 mm；模糊RBF控制误差为0.4 mm。

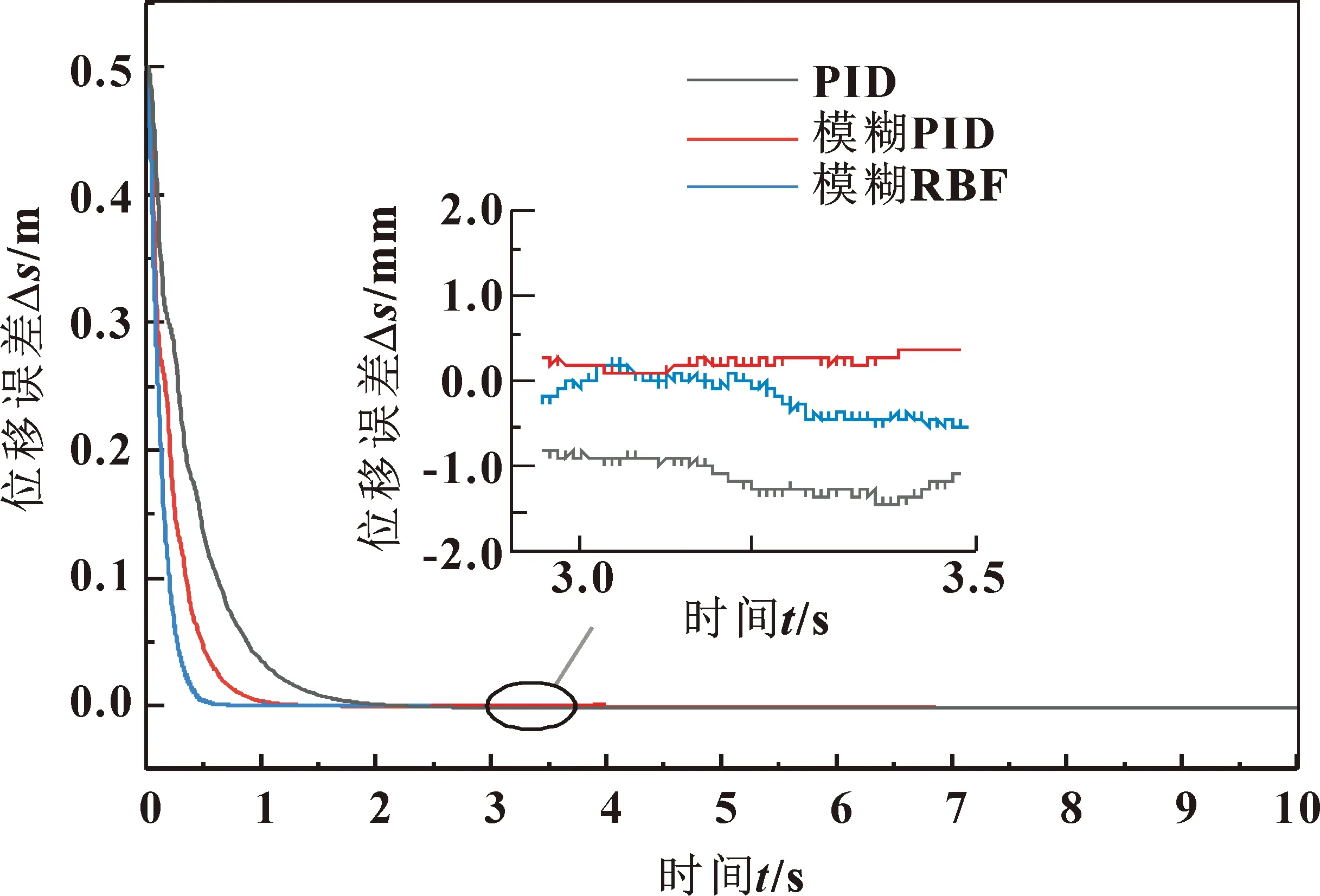
图8 误差响应曲线

当系统在2 s时受到扰动，其响应曲线如图9所示，PID波动值为14 mm，调整时间为0.7 s；模糊PID波动值为5 mm，调整时间为0.5 s；模糊RBF波动值2 mm，调整时间为0.2 s。可以看出模糊RBF控制系统抗干扰能力强，鲁棒性最好。

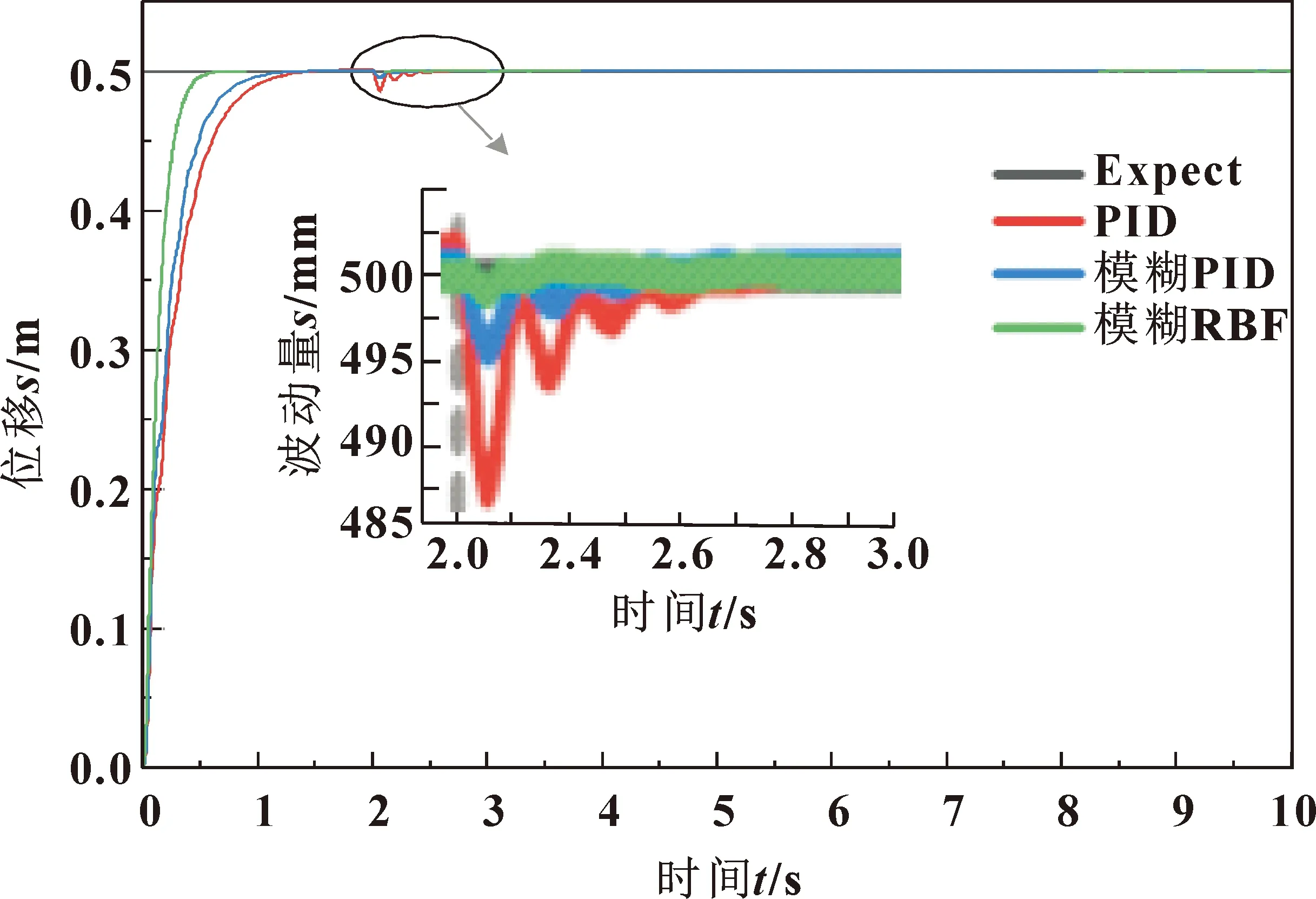
图9 系统加入干扰响应曲线

4.2 模糊RBF交叉耦合同步策略验证

采用交叉耦合控制策略对两缸同步性能进行验证，系统结构如图10所示。两液压缸同步曲线如图11所示，同步误差如图12所示。从图12可以看出：缸1与缸2同步跟踪性能较好，同步误差在0.5 s时出现较大波动，最大同步误差为4.5 mm，0.5 s之后同步误差很快调整，控制在-0.7～1.2 mm之内，控制精度和同步误差达到预期效果。

图10 模糊RBF交叉耦合程序

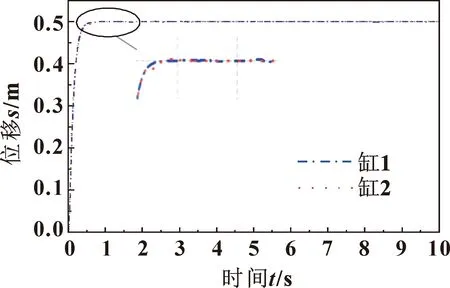
图11 交叉耦合模糊RBF同步位移跟踪曲线

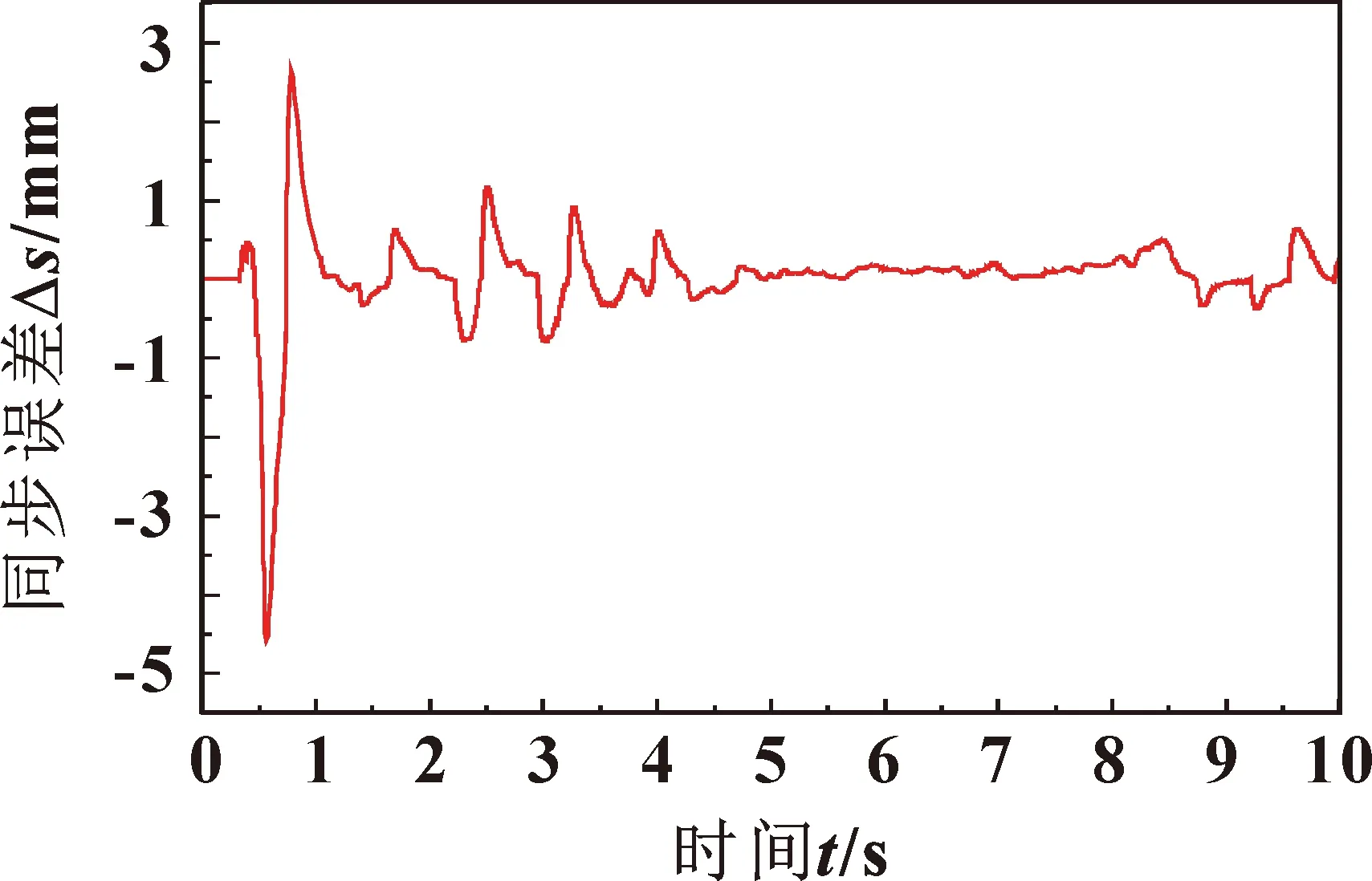
图12 模糊RBF交叉耦合同步跟踪误差曲线

5 结论

针对液压式压裂泵液压缸不同步现象，提出采用模糊RBF+交叉耦合的控制策略。经仿真验证，该控制策略控制效果可观，为后期液压式压裂泵同步控制实验提供理论基础。

(1)以阀控缸为研究对象，搭建数学模型，分析模糊控制与RBF神经网络控制的优劣，提出模糊RBF神经网络+交叉耦合控制策略。

(2)设计传统PID位置跟踪控制器、模糊PID位置跟踪控制器、模糊RBF位置跟踪控制器控制伺服阀。经仿真验证，在不加干扰时，模糊RBF在0.7 s达到稳定状态，模糊RBF相比传统PID控制响应时间缩短63.2%；与模糊PID相比，响应时间缩短36%，在响应速度和控制精度方面模糊RBF最佳；在2 s时加入扰动时，PID波动值为14.0 mm，调整时间为0.7 s；模糊PID波动值为5.0 mm，调整时间为0.5 s；模糊RBF波动值2.0 mm，调整时间为0.2 s。3个控制器中模糊RBF控制器的鲁棒性明显优于其他两种控制器，其控制效果最佳，达到预期效果。

(3)同步控制器选用交叉耦合同步控制，经仿真验证，模糊RBF交叉耦合同步控制最大同步误差为4.5 mm，同步误差基本控制在-0.7～1.2 mm之内，控制精度和响应速度达到预期目标。