节流孔直径和分布对静压气浮主轴稳态性能的影响

马城辉，王鹏峰，朱远哲，高翔，李孝禄，李运堂

(1.中国计量大学机电工程学院，浙江杭州 310018；2.中国计量大学现代科技学院，浙江杭州 310017)

0 前言

随着高速加工技术的不断进步，现代机械制造业向高速、高精度和高效率的方向快速发展，相对于传统油脂润滑，静压气浮主轴因具有转速快、精度高、无污染和摩擦损耗小等优点，成为高速机床加工设备的核心部件[1-3]。

静压气浮主轴以气体作为润滑介质，气体可压缩性导致主轴承载能力和刚度偏低，很难适用于大承重工况，因此，多年来，国内外学者对影响静压气浮主轴承载能力和刚度等稳态性能的结构参数和工作参数进行了大量研究。CUI等[4]采用有限元法研究了节流孔直径对静压气浮主轴承载能力和刚度的影响，认为随节流孔直径增加，主轴承载能力提高、刚度先增大后减小。GAO等[5]发现主轴转速超过20 000 r/min，承载能力随节流孔排数增加而降低。CHEN等[6]认为平均气膜厚度较小时，增加节流孔处的沟槽面积有利于增大静压气浮主轴承载能力和刚度。程志勇等[7]以静压气浮主轴为研究对象，发现当单排节流孔数量为8时，主轴承载能力最佳。李育隆等[8]认为静止时静压气浮主轴的承载能力随节流孔数增加而增大，节流孔数越多，承载能力提升幅值越小。SONG等[9]指出静压气浮主轴表面螺旋槽结构有利于提高承载能力和稳定性。LI等[10]提出具有更高承载能力新型静压气浮主轴结构，采用有限差分法计算其承载能力。XIAO等[11]指出在高速大偏心率时，转速越高，静压气浮主轴承载能力和刚度越大。ZHANG等[12]采用有限差分法分析了静压气浮主轴的稳态性能，结果表明：随着偏心率和转速的增大，主轴承载能力提高、高度角先增大后减小。胡俊宏等[13]认为增加转速、偏心率和供气压力均能提高主轴承载能力。崔海龙等[14]研究发现静压气浮主轴的承载能力和刚度随供气压力的提高而增加。

随着对静压气浮主轴的研究深入，学者发现加工误差和装配误差影响主轴稳态性能。WANG等[15]研究发现静压气浮主轴的承载能力和刚度随正弦波纹幅值增大而减小。SHI等[16]采用有限差分法研究转子轴套装配倾角对静压气浮主轴稳态性能的影响，结果表明：在小偏心率下，承载能力和刚度随着倾角的增大而减小。

针对静压气浮主轴结构参数对其性能的研究，现有文献只考虑节流孔直径、数量以及排数的影响，关于节流孔直径变化和位置分布对主轴稳态性能影响的研究很少。本文作者采用有限元法分析静压气浮主轴稳态性能，研究转速、偏心率和平均气膜厚度不同时直径系数(相邻节流孔直径比)和分布系数(相邻节流孔间隔比)对主轴性能的影响，为优化主轴结构、提高主轴稳态性能提供参考。

1 有限元法求解静压气浮主轴性能

1.1 静压气浮主轴结构

静压气浮主轴以气体作为润滑介质，外部压缩气体通过节流孔进入主轴间隙，形成一定承载能力和刚度的气膜，支承转子浮于轴套中。传统静压气浮主轴结构如图1所示，节流孔直径相同且均匀分布于轴套圆周上，hm、ω、c、d、D、L和φ分别为平均气膜厚度、转速、偏心距、节流孔直径、主轴直径、主轴长度和高度角，x、y和z分别表示主轴轴向、径向和周向坐标，h和θ分别为静压气浮主轴圆周内任意点的气膜厚度和该点与轴心连线与y轴负半轴的夹角。

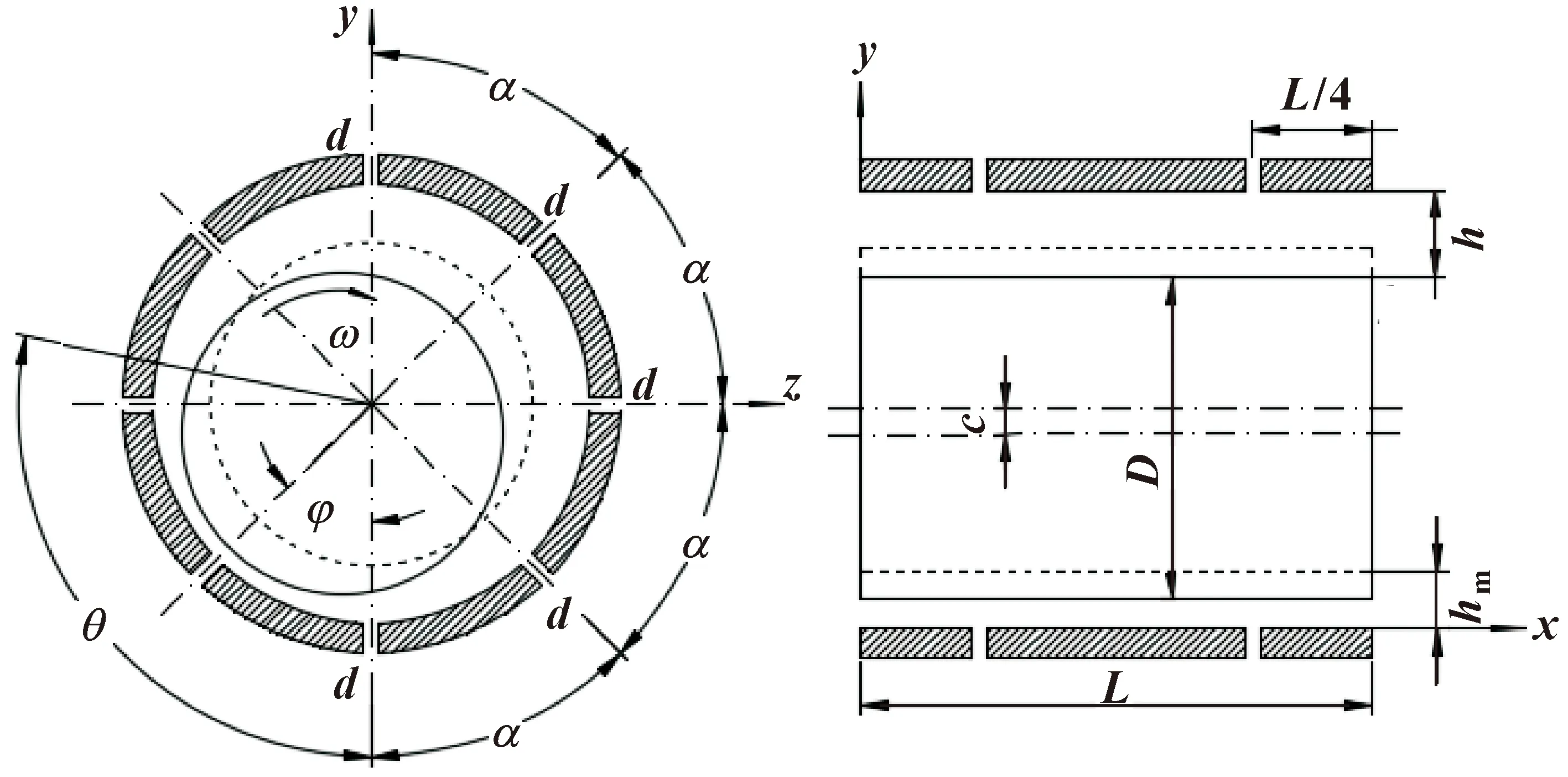
图1 传统静压气浮主轴结构

(1)

为分析节流孔直径和分布对静压气浮主轴性能的影响，提出如图2所示的新型主轴结构，节流孔直径由d1至di逐渐减小，di=d1·γi-1(i=2，3，…，n)，γ为直径系数。节流孔i到i+1间的夹角为αi(i=1，2，3，…，n-1)，αi+1=δαi且α1+α2+…αn-1=180°，δ为分布系数。

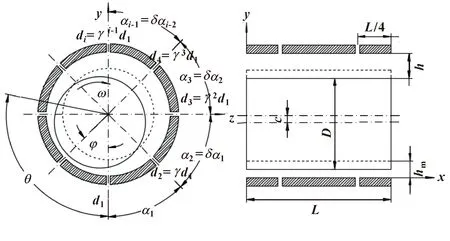
图2 新型静压气浮主轴结构

1.2 主轴性能的计算方法

根据气体运动方程、连续性方程和状态方程建立气膜内量纲一稳态雷诺方程

(2)

定义量纲一压方函数

(3)

代入式(2)可得

(4)

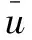
将计算域展开成如图3所示的平面网格，并划分成2mn个如图4所示三角形单元体。

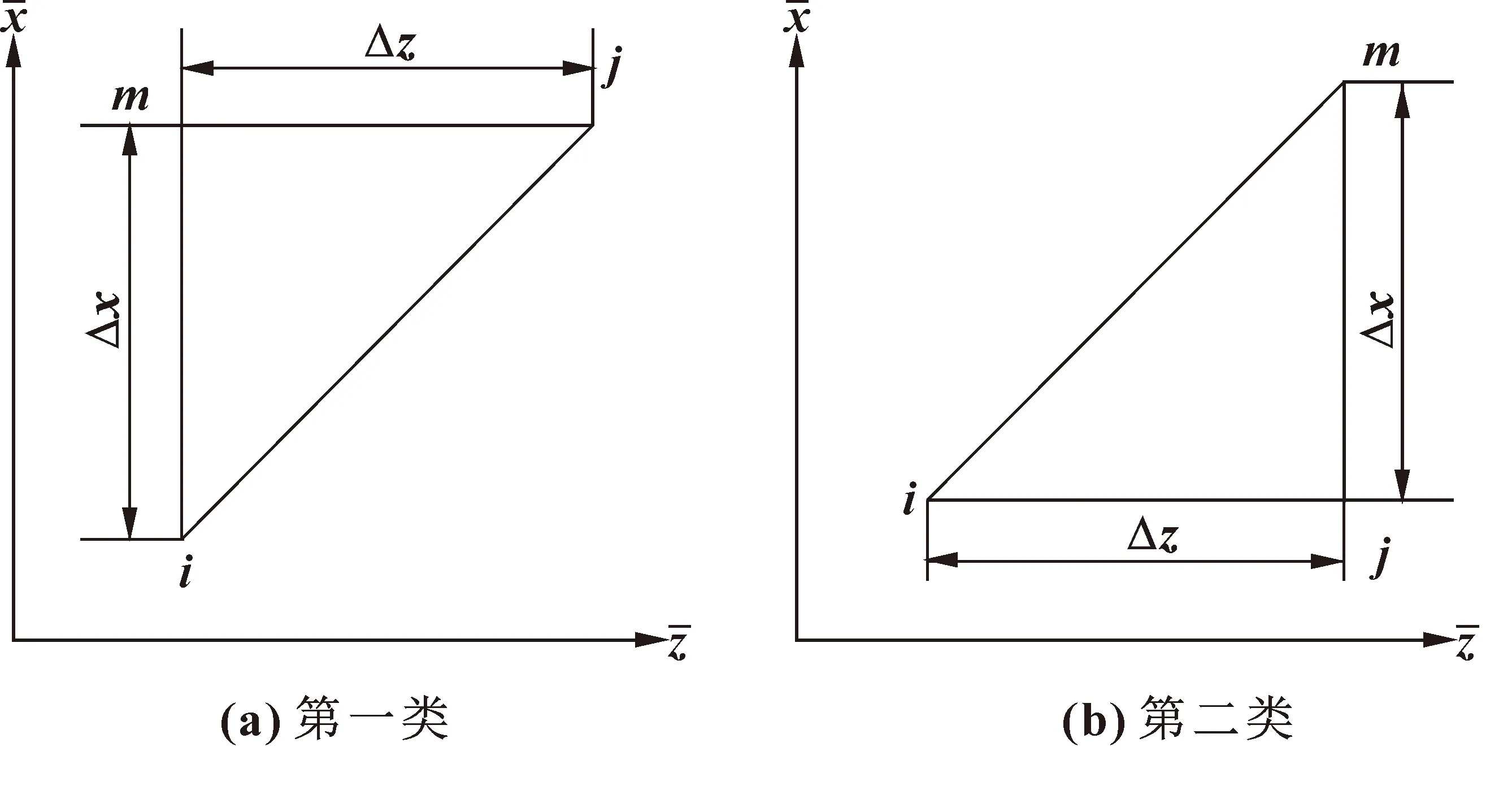
图4 两类三角形单元体

由图3可知包含三种边界条件

式中：ns是对称边界的法线；pd为节流孔出口处气体压力。

应用伽辽金加权余量法和弱解公式得

(5)

将式(5)写成三角形单元体面积积分之和

(6)

f=NeTfe

(7)

式中：

δf=NeTδfe=δfeNe

(8)

f1/2=NeT(f1/2)e

(9)

(10)

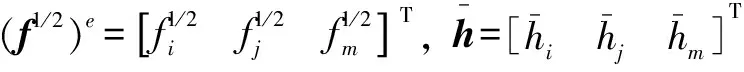
将式(7)—(10)代入式(6)得式(11)与(12)

(f1/2)e=0

(11)

(12)

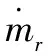
(13)

ψr=

(14)

βk=[2/(k+1)]k/(k-1)

式中：k为气体常数，空气取k=1.4。

将式(11)的积分项展开，得到量纲一雷诺方程的泛函式(15)，采用超松弛迭代法求解式(15)，得到未知节点压力，求出每一个单元体的量纲一承载能力式(16)。

(15)

(16)

由三角形单元体的量纲一承载能力可求得y、z方向上的量纲一承载能力

(17)

(18)

式中：k=1，2，3，…，m。由y、z上的量纲一承载能力可求得静压气浮主轴总的量纲一承载能力

(19)

高度角

(20)

对量纲一承载能力进行量纲化后得到静压气浮主轴的承载能力：

(21)

刚度：

(22)

2 结果与讨论

2.1 计算参数

计算不同结构下静压气浮主轴承载能力、刚度和高度角，分析直径系数和分布系数对主轴稳态性能的影响。计算参数如表1所示，结构Ⅰ为均匀分布等节流孔直径的传统结构；结构Ⅱ分布系数取1，直径系数取0.9～0.98；结构Ⅲ分布系数取1.05～1.2，直径系数取1；结构Ⅳ分布系数取1.05～1.2，直径系数取0.9～0.98。主轴结构参数及气体特性如表2所示。

表1 不同结构静压气浮主轴计算参数

表2 主轴结构参数及气体特性

2.2 网格数的选取

采用有限元法时，计算域划分网格数越多，计算结果精度越高，消耗时间越多。为保证计算精度，减小计算时间，对比分析3种不同网格数的计算结果。方案A将计算域划分成128×40的网格，生成10 240个单元体；方案B划分成192×60的网格，生成23 040个单元体；方案C划分成256×80的网格，生成40 960个单元体。取ω=0 r/min、hm=30 μm、e=0.3、d=0.2 mm，主轴结构参数及气体特性如表2所示。表3列出了传统结构主轴在不同网格数下的承载能力，可知：方案A和方案B与计算精度最高的方案C相比，相对误差均小于1%。在计算结果相差较小时，选择网格数少的方案以减少计算时间，因此采用128×40的网格进行计算。

2.3 计算结果验证

为验证有限元法计算结果的准确性，与文献[17]进行各节流孔质量流量和主轴承载能力的对比，主轴结构参数及气体特性如表2所示。对比数据如表4所示，可以看出在相同条件(hm=19.05 μm、ω=0 r/min、d=0.15 mm、e=0.5)下，各节流孔处流量系数的相对误差均小于0.5%，承载能力的相对误差仅为0.006%，对比结果证明有限元计算结果的准确性。

表4 计算结果对比

2.4 气体压力分布

转速为零，由于结构对称性，气体压力沿轴向和周向对称分布，hm=30 μm、e=0.2、d=0.2 mm，不同结构的静压气浮主轴气体压力分布如图5(a)—(d)所示，轴向与周向坐标为计算域中的网格位置，最大气体压力和最小气体压力分别出现在节流孔1处和节流孔5处。

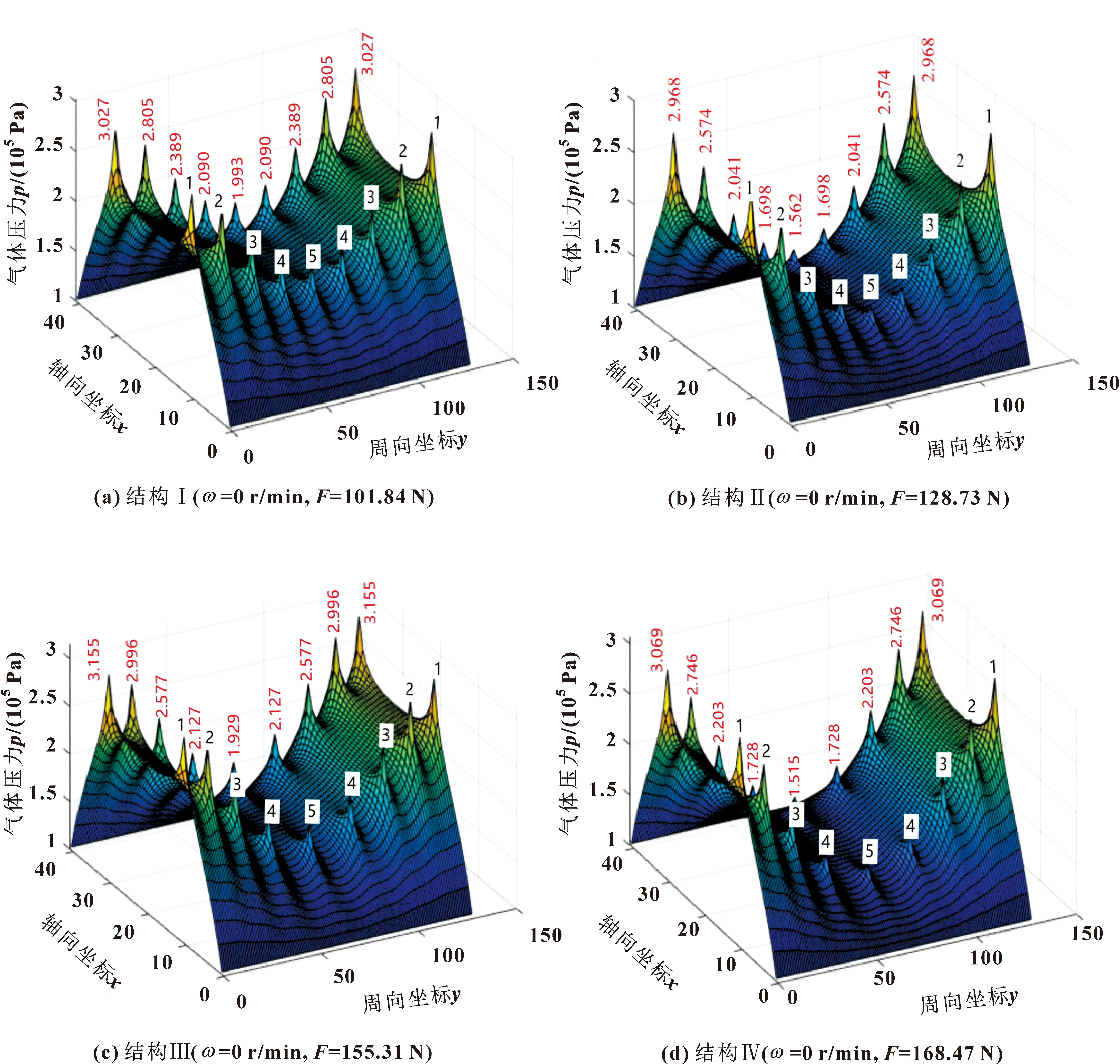
图5 不同主轴结构的气体压力分布

对比图5(a)(b)可知：当节流孔均匀分布时，直径系数的减小造成节流孔1处的气体压力升高，节流孔5处的气体压力降低，导致孔1和孔5的压力差明显增大，承载能力由101.84 N增加至128.73 N，表明降低直径系数γ能提高主轴承载能力。对比图5(a)(c)，当节流孔直径相同时，增加分布系数增大了节流孔1和节流孔5处的压力差，同时承载能力由101.84 N增加至155.31 N，表明增大分布系数δ能提高主轴承载能力。对比图5(a)(d)可知，增大分布系数δ同时减小直径系数γ，承载能力由101.84 N变化至168.47 N。对比4种结构的气体压力分布及承载能力可知，结构Ⅱ、结构Ⅲ、结构Ⅳ均能增大主轴内部气体压力差，提高主轴承载能力，其中结构Ⅳ对主轴内气体压力影响最大，提高主轴承载能力最显著，结构Ⅲ对主轴气体压力和承载能力的影响大于结构Ⅱ。结果表明：减小直径系数和增大分布系数有利于提高主轴承载能力。

2.5 主轴承载能力和刚度分析

图6为不同平均气膜厚度、偏心率、转速时直径系数和分布系数对主轴承载能力的影响。由图6可知：相同参数下，结构Ⅱ、结构Ⅲ相比结构Ⅰ具有更大的承载能力，结构Ⅱ的承载能力随直径系数的增大而降低，结构Ⅲ的承载能力随分布系数的增大而提高。平均气膜厚度越小，主轴承载能力越大，同时直径系数和分布系数对承载能力的影响越显著，对比图6(a)(b)和(d)(e)可知，偏心率对主轴承载能力影响较大，偏心率越高，主轴承载能力越大。对比图6(b)(c)和(e)(f)可知，当转速从0 r/min提高至2×104r/min时，主轴承载能力变化不明显，表明当转速低于2×104r/min时，转速变化对主轴承载能力的影响较小。

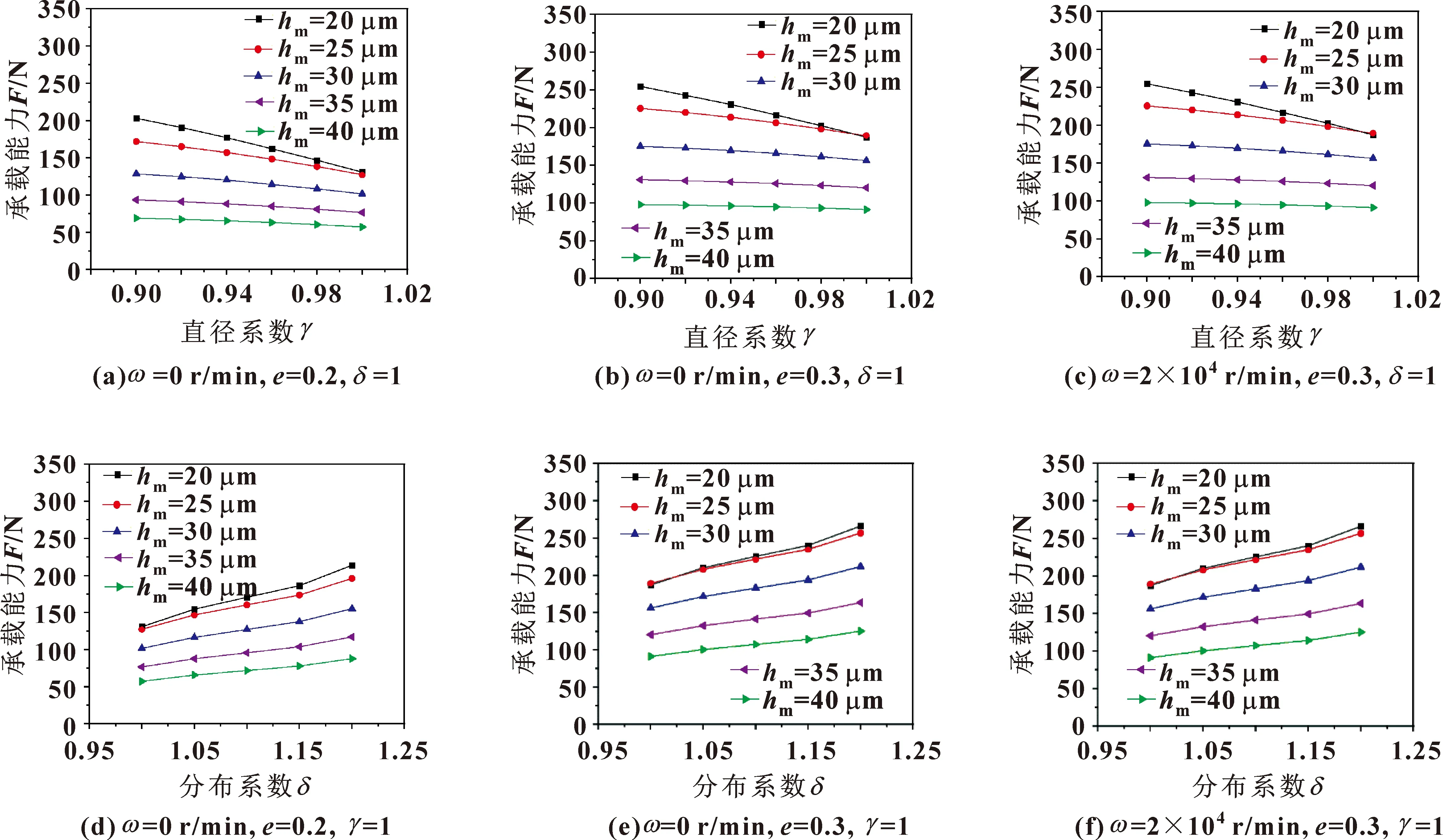
图6 不同工作参数下直径系数和分布系数对承载能力的影响

图7为不同平均气膜厚度、偏心率、转速时直径系数和分布系数对主轴刚度的影响。由图7可知：当平均气膜厚度较小时，结构Ⅱ、结构Ⅲ的刚度明显高于结构Ⅰ。从图7(a)—(c)和(d)—(f)看出：结构Ⅱ的刚度随直径系数的增加而减小，结构Ⅲ的刚度随分布系数的增加而增大；平均气膜厚度越小，主轴刚度越大。对比图7(a)(b)和(d)(e)可知：与承载能力不同，增大偏心率会导致主轴刚度降低，且偏心率对刚度的影响在平均气膜厚度小时比较明显，当平均气膜厚度大于30 μm时，偏心率对刚度的影响可忽略。对比图7(b)(c)和(e)(f)可知，当转速从0 r/min提高至2×104r/min时，主轴刚度变化不明显，表明当转速低于2×104r/min时，转速变化对主轴承载能力的影响较小。

2.6 高度角分析

高度角特性表征了稳定工作时转子质心与轴套质心的相对位置。由图8可知：当节流孔均匀分布时，直径系数增大，主轴高度角增大；当节流孔直径相同时，增大分布系数主轴高度角减小。随着平均气膜厚度的增大，高度角先减小后增大，且平均气膜厚度越大，直径系数变化对高度角的影响越小。对比图8(a)(b)和(d)(e)可以看出：当气膜厚度小于30 μm时，增大偏心率，主轴的高度角增加；当气膜厚度大于30 μm时，随着偏心率的增大，主轴高度角减小。对比图8(b)(c)和(e)(f)可知：提高主轴转速能增大主轴高度角，且平均气膜厚度越小，转速对高度角的提升越显著。

3 结论

采用有限元法求解静压气浮主轴内气体流动雷诺方程，研究不同直径系数和分布系数时主轴承载能力、刚度和高度角，并探讨不同工作参数对不同结构主轴性能的影响，得出结论：

(1)与传统主轴相比，变节流孔直径和节流孔非均匀分布主轴具有更大的承载能力、更大的刚度和更小的高度角：直径系数越小，主轴承载能力和刚度越大，高度角越小；分布系数越大，主轴承载能力和刚度越大，高度角越小。

(2)随着平均气膜厚度的增大，主轴承载能力和刚度减小，高度角先减小后增大；平均气膜厚度越大，承载能力、刚度和高度角随直径系数和分布系数的变化幅值越不显著。

(3)在小偏心率下(e<0.5)，当直径系数和分布系数取值一定时，偏心率增大，主轴承载能力增大；当气膜厚度小于30 μm时，随着偏心率的增大，主轴刚度减小而高度角增加；当气膜厚度大于30 μm时，随着偏心率的增加，主轴高度角减小而刚度变化不明显。

(4)在低转速时(ω<2×104r/min)，转速的增大对主轴承载能力和刚度的影响不显著，但会导致主轴高度角增大。