大型液压成形装备快降运动曲线的平稳性设计与控制

严建文，杨晨，刘琼，李磊，秦永红，陈黄祥

(1.安徽理工大学机械工程学院，安徽淮南 232000；2.合肥合锻智能制造股份有限公司，安徽合肥 230601；3.合肥工业大学机械工程学院，安徽合肥 230009)

0 前言

大型液压成形装备活动横梁在下降过程中需要快速地完成合模，以防止材料温度变化等原因造成成形质量的问题。目前大型液压成形装备活动横梁快降过程存在速度突变，导致液压系统产生较大的冲击和偏载。针对冲击和偏载问题，国内外学者在液压系统结构、控制算法和运动曲线等方面进行了深入的研究。

在液压系统结构优化方面，部分学者采用调节插装阀开度[1]、增大卸载管路[2]、应用蓄能器[3]以及顶置式缓冲装置[4]的方式，在一定程度上取得了缓解冲击振动的效果。与改变液压元件方案不同，CHEN等[5]利用三通比例阀，设计了一种新型电液控制系统，有效降低了液压机锻造过程中的振动和冲击问题。在实际应用中需要频繁调节阀口的开度，因此对阀体会产生一定的影响。LYU等[6]为了实现液压系统的高精度位置跟踪和较高运动性能要求，设计了独立阀控和泵控组合的控制方案，并通过实验验证了方案的可行性。组合控制需要对多个目标进行实时控制，对控制要求较高。因此，系统结构上的优化研究能够减轻活动横梁快降过程中的冲击和振动问题，但是传统结构优化方案对液压元件的控制性能要求较高。

在控制算法优化方面，预测型多模式控制技术[7]、TS神经网络控制方案[8]和径向基函数神经网络技术[9]均得到了相对较好的稳定性控制结果。但仍存在跟踪误差，无法适应多变的生产环境。TONY THOMAS等[10]利用滑模控制器对液压的实际运动进行跟踪控制，有效地减轻了超调震荡现象。由于传统滑模控制的滑模模型通常被设计为线性超平面，仅能保证系统状态的渐近收敛，因此可以进一步优化相关控制算法的应用。SHAO等[11]在此基础上设计了一种基于SMOD的自适应反推终端滑模控制器，在液压位置伺服控制的仿真验证中提高了系统的鲁棒性。综合分析不同控制算法的方案，实际生产中难以单独引用控制算法完成对活动横梁快降运动的控制过程，无法满足活动横梁快降运动的控制需求。

在运动曲线方面，LI等[12]分析了直驱伺服压力机中运动曲线误差对冲压性能的影响问题，得出了可以使用适当误差准则减小后续误差的理论结果，需要在研究的基础上加强对误差曲线的设计优化工作。王俊、李明[13]基于工艺要求对伺服压机的行程曲线进行了优化，对运动过程中产生冲击的点进行三次B样条曲线拟合，得到较好的工艺运动曲线，减小了装备的噪声、振动和冲击。根据插值拟合的曲线在一定程度上改善了速度拐点的冲击现象，但是整体的运动过程在理论上仍然存在冲击和振动现象。DU等[14]针对活动横梁变速下落运动的研究，首先分析了三次多项式运动轨迹。但是三次曲线对于速度骤变引起的冲击效果应对能力较差，不能彻底改善运动过程中产生的冲击问题。其次，采用多岛遗传算法对无冲击最速下降曲线进行优化，得到合理的五次运动曲线方程[15]，有效地应对了活动横梁快降中存在的冲击问题。上述研究表明，通过运动曲线的优化能够更好地减缓运动冲击，但是如何在减小冲击的同时提升快降速度、提高生产效率，仍有待进一步研究。

针对上述问题，本文作者设计大型液压成形装备快降液压系统，采用NSGA-II算法优化活动横梁的五次运动曲线，设计模糊PID控制器。通过仿真和实验进行验证，以期得到适用于大型液压成形装备快降运动规律与平稳性控制的方法，解决活动横梁高速运动中产生的较大冲击问题。

1 液压系统建模

大型液压成形装备中活动横梁的运动过程基本分为7个阶段，其中T1至T2为快降阶段，T2至T3为减速阶段，T3至T4为工进阶段，T4至T7为压制及保压阶段，T7至T10分别为开模、快速回程和减速阶段，如图1所示。传统方案活动横梁运动过程中设置多处减速点，使活动横梁在T4时达到合适的压制速度，但是活动横梁存在较大的惯性，会在速度拐点处产生较大冲击。因此，为了减轻运动冲击，选择难以解决的快降起点至合模过程的冲击问题进行分析。

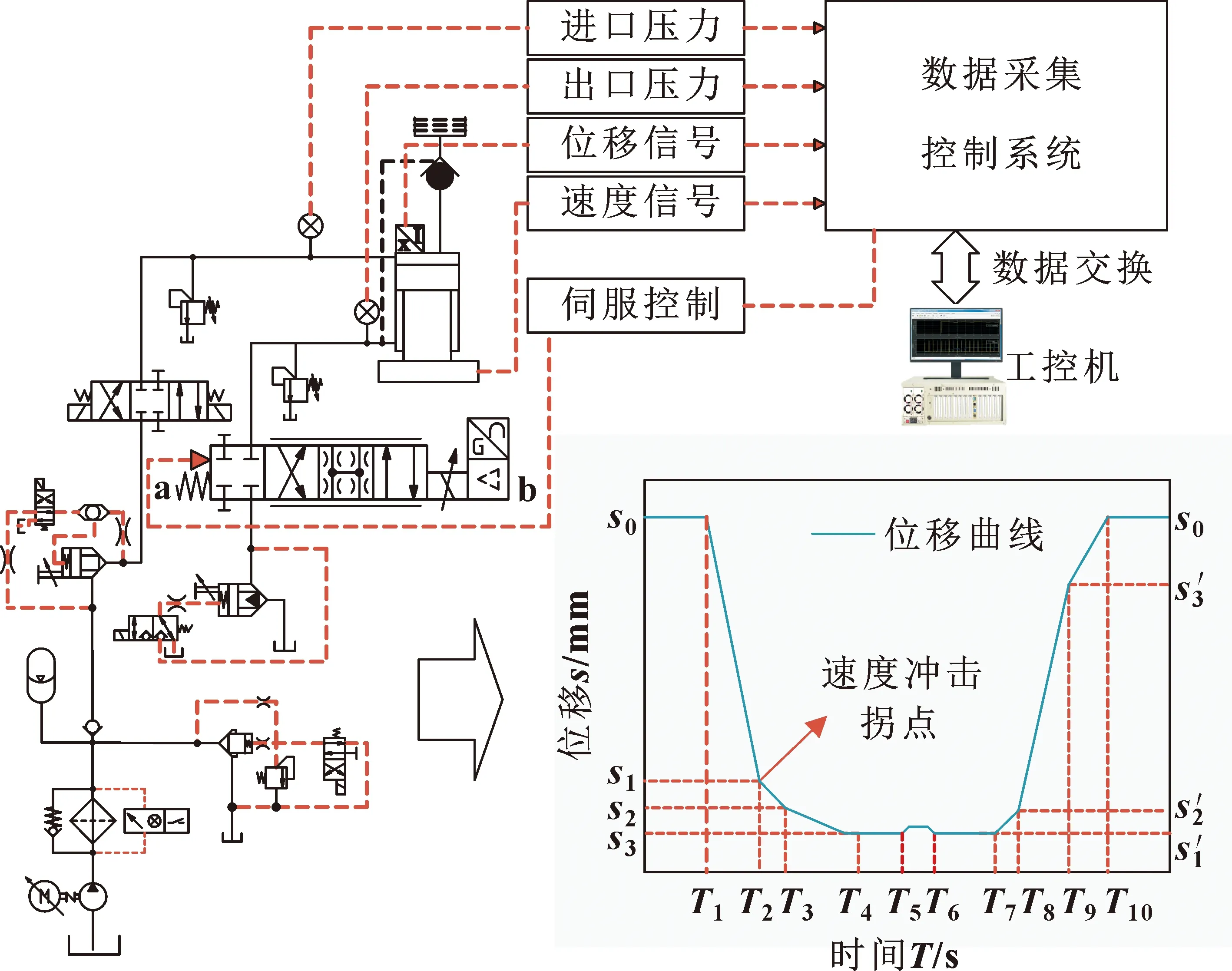
图1 液压系统和工作过程位移

1.1 液压系统快降过程建模

为了在活动横梁快速下降过程中对运动曲线实现精准控制，重新设计了成型液压机的液压油路及控制系统，如图1所示。在回油路上设置高频响阀，精确控制油路中的流量大小。采用带有内置位移传感器的油缸，由计算机处理位移信号并输出控制信号，实现对活动横梁下降过程中速度和压力的实时稳定控制。为了保证活动横梁快速下降的过程中系统压力和管路中流量的稳定性，在进油路中设置充液阀与油箱直接连接，以满足快下过程中系统的稳定性要求。

由于活动横梁快降过程中无负载力作用，可得该伺服系统框图，如图2所示。

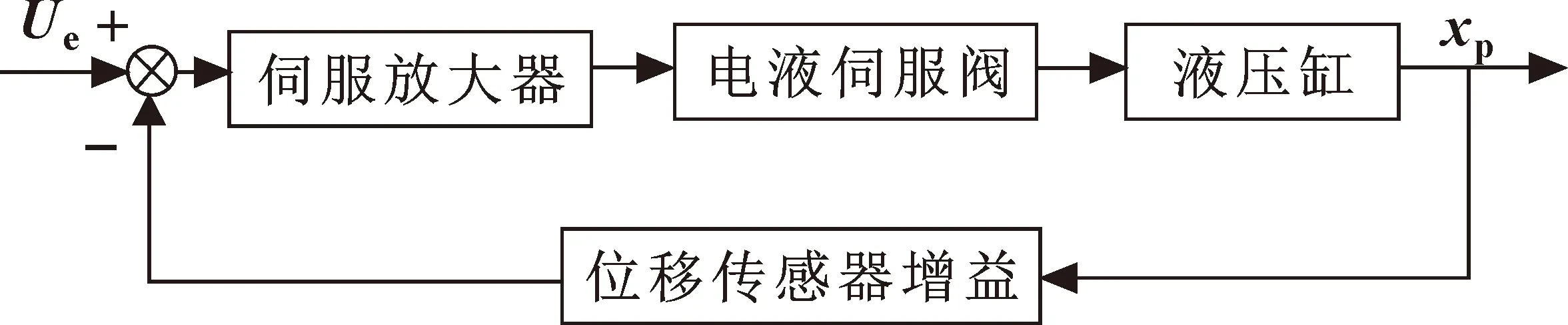
图2 伺服系统位移反馈框图

在实际运行中，活动横梁快降系统主要以电液伺服阀[16]控制液压缸位移的方式实现。系统结合相关参数，可将常用电液伺服阀近似成二阶振荡系统[17]，其中电液伺服阀的开环传递函数如式(1)所示

(1)

其中：Ksv为伺服阀的流量增益；Gsv为Ksv=1时的伺服阀传递函数；ωsv为伺服阀的固有频率；ξsv为伺服阀的阻尼比。

根据实况分析，活动横梁快降过程中外负载为0，根据分析可得液压缸位移xp对阀的输入指令xv的传递函数为

(2)

其中：Kq为流量系数；Ap为液压缸活塞有效面积；ωh为液压缸固有频率；ξh为液压阻尼比，一般取0.1～0.2。

此外，伺服放大器的电流ΔI与输入电压Ug近似成比例，采用伺服比例放大器增益Ka表示：

(3)

位移传感器增益数学模型为

(4)

其中：If为反馈电流信号；Y为液压缸活塞位移。联合式(1)—(4)可得到高频响比例伺服阀阀控液压缸系统传递函数，如图3所示。

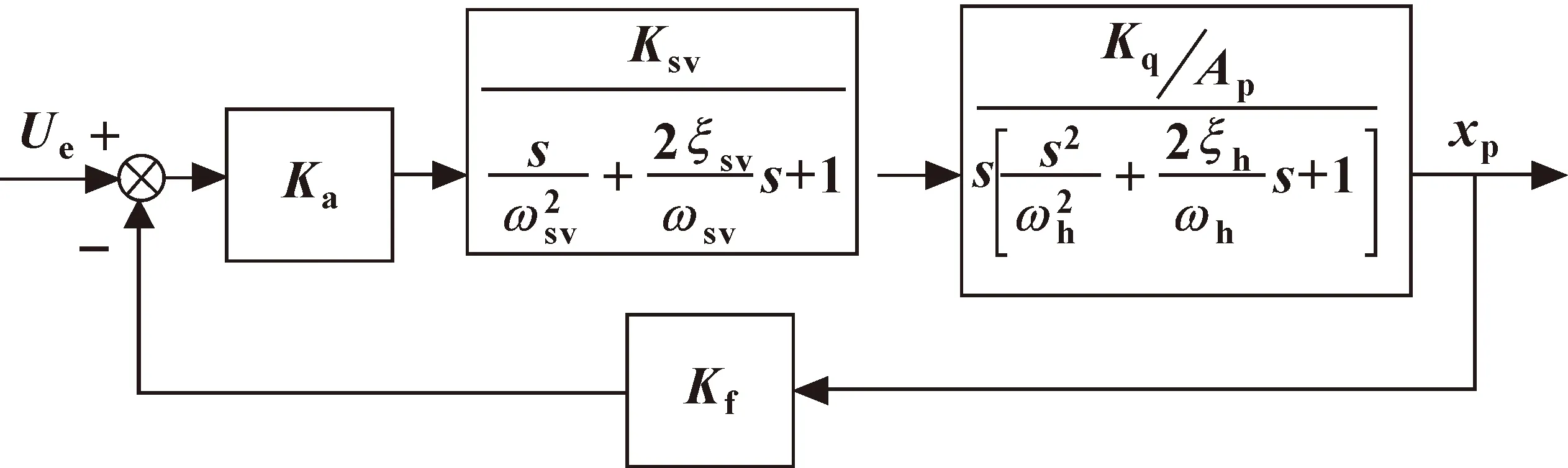
图3 液压回路控制系统传递函数框图

由图3可得系统开环传递函数为

(5)

其中：Kv=KqKfKaKsv/Ap。

1.2 快降曲线的平稳性设计

运动轨迹曲线优化在工业上已经进行多方面的应用，其中以三次B样条曲线[18]、贝塞尔曲线[19]和五次样条曲线[20]为主。文中选择应用性较强的五次样条曲线建立目标运动曲线函数，优化五次运动曲线模型，以得到活动横梁最佳下降规律。

以最短运动时间和最小冲击为约束条件，列出五次运动曲线一般表达(式(6))和约束方程组(式(7))：

(6)

(7)

其中：A0、A1、A2、A3、A4和A5为多项式系数；t为活动横梁运动时间；Y为运动位移；v为运动速度；a为运动加速度；J为加加速度。

根据图1所示活动横梁下降运动曲线的运动特点可知，在快速下降过程中所设计的五次运动曲线分为变加速和变减速2个运动阶段。结合运动起点和终点状态，五次运动曲线优化的初始条件设置如下：

起点条件：Y(t0)=Y0，v(t0)=v0，a(t0)=a0,J(t0)=J0。终点条件：Y(ts)=Ys，v(ts)=vs，a(ts)=as，J(ts)=Js。其中：t0为起点时间；ts为运动终点时间；Y0、v0、a0和J0为起点位移、速度、加速度和加加速度，相对应的Ys、vs、as以及Js为运动终点处的位移、速度、加速度和加加速度。

为了得到最优解的结果，需要给出合理的约束条件。活动横梁在理想极限状态下做自由快降运动，并根据参数设置五次运动曲线优化的状态约束条件。根据已知系统参数对最大加速度、最大速度进行求解，相关参数的求解过程如下：

(8)

式中：F为油缸活塞杆所受的滑块重力；F1为快降时进油口的负压对活塞的拉力；F2为快降时出油口处产生的压力反作用力；f为活塞杆运动时所受阻力；m为滑块质量；a1为活动横梁下落过程中的平均加速度；t1为下降时间；s为理论下降位移；g为重力加速度；p1为油缸进油口的压力；A1为进口活塞面积；p2为油缸出油口的压力；A2为出油口活塞杆底部与油液接触面积；fc为油缸黏性摩擦系数；v1为活塞杆运动速度；F3为减速时油缸出油口对活塞杆的最大反作用力；f′为减速时油缸所受最大摩擦力；a2为活塞杆的最大减速度；p3为油缸出油口所受最大压力。

1.3 控制器设计

为了研究新型运动模型对减小快降冲击、提高位移精度和克服非线性运动的效果，设计了自调整模糊PID控制器。具有良好自适应特性、结构简单和工作稳定性的模糊PID控制器[22-23]能够弥补PID控制器的不足，与系统和运动模型匹配。

研究中设计的模糊PID控制器以位移误差建立PID模块与模糊逻辑控制器的相互作用系统。以位移误差和误差变化率作为输入，经模糊逻辑控制器输出实时的Kp、Kd和Ki，如图4所示。

图4 模糊PID控制器作用流程

通过模糊PID控制器的特性分辨位移误差和误差变化率与设定模糊控制器输出值，控制高频响阀口开度。然后，根据相应的控制要求完成模糊规则的设定和输出参数的量化。其中，模糊规则决定着模糊控制器的运行质量，不同的运动情况需要具体设置特定的模糊规则。为了实现高精度控制，系统模糊规则设定如表1所示。

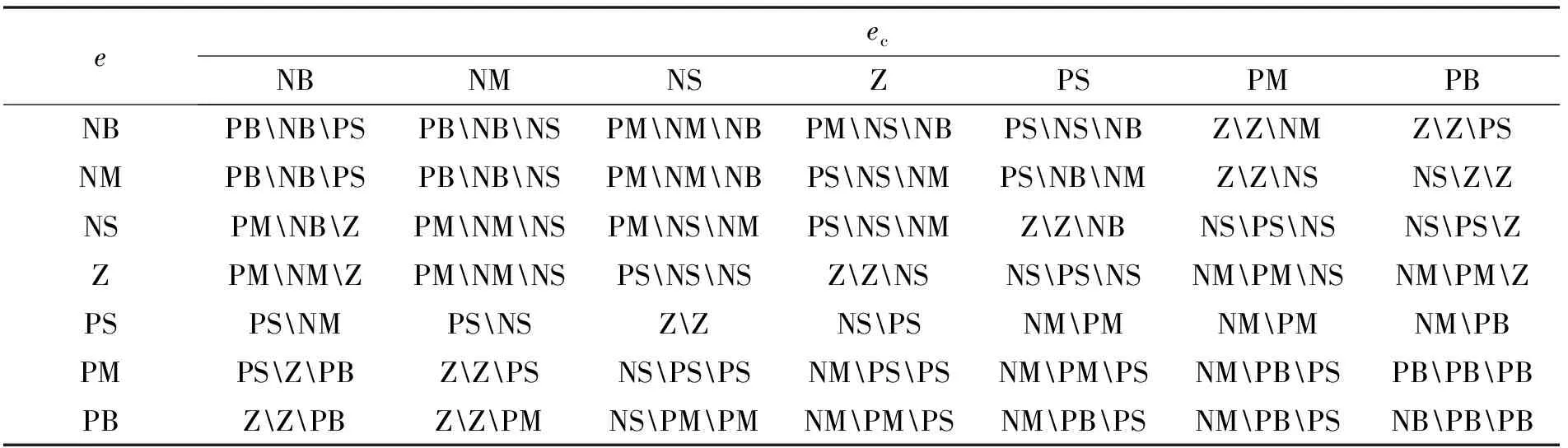
表1 高频响阀模糊PID控制中Kp、Ki、Kd模糊规则

2 AMESim 和Simulink联合仿真

2.1 仿真系统的结构

根据图1所示液压系统原理，在AMESim中构建液压系统仿真模型，同时在Simulink中建立控制系统，控制系统建模如图5所示，具体液压元件仿真参数设定如表2所示。通过软件联合[24]，进行仿真测试。

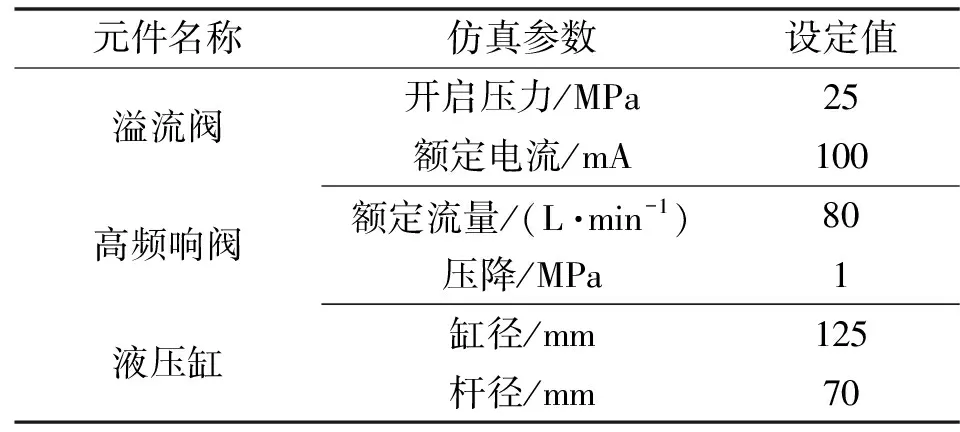
表2 液压系统仿真中主要液压元件参数

图5 仿真控制原理

此外，结合控制系统设计及活动横梁运动范围参数，最终设定模糊控制器的输入跟踪误差e和误差变化率ec的量化论域为(-0.6，-0.4，-0.2，0，0.2，0.4，0.6)。在实验仿真中得出输出变量比例系数Kp、积分系数Ki和微分系数Kd的量化论域。Kp为(0，5，10，15，20，25，30)，Ki为(0，0.09，0.17，0.25，0.33，0.5)，Kd为(0，0.05，0.1，0.15，0.20，0.25，0.3)。其次，量化因子是对误差e和误差变化率ec的转化参数，参照油缸行程的设定0.6 m，可以得出Ke=0.6/0.6，Kec=0.6/0.6。

2.2 曲线优化求解

针对建立的模型、约束条件和已知参数选取NSGA-II 算法[21]，求解方程最优解。其中：初始条件Y0=0 m；v0=0 m/s；a0=0 m/s2；t0=0 s；Ys=0.6 m；amax=6 m/s2。优化得到满足最快速度、最小冲击和最短时间条件的最优解，如图6所示。

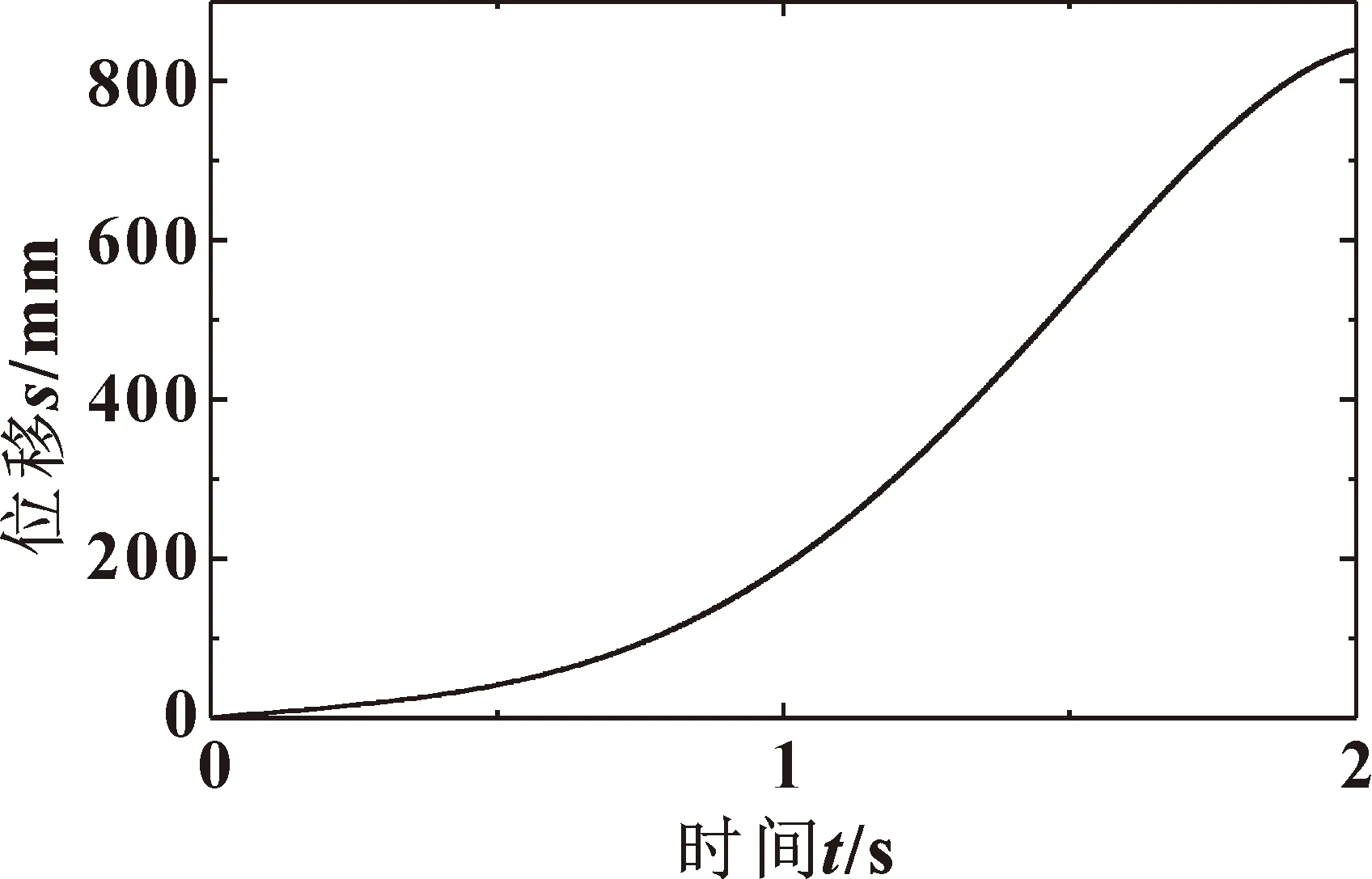
图6 活动横梁快降优化运动曲线

2.3 仿真结果分析

控制模型对优化后五次运动曲线的跟踪，仿真结果与跟踪误差分别如图7、8所示。

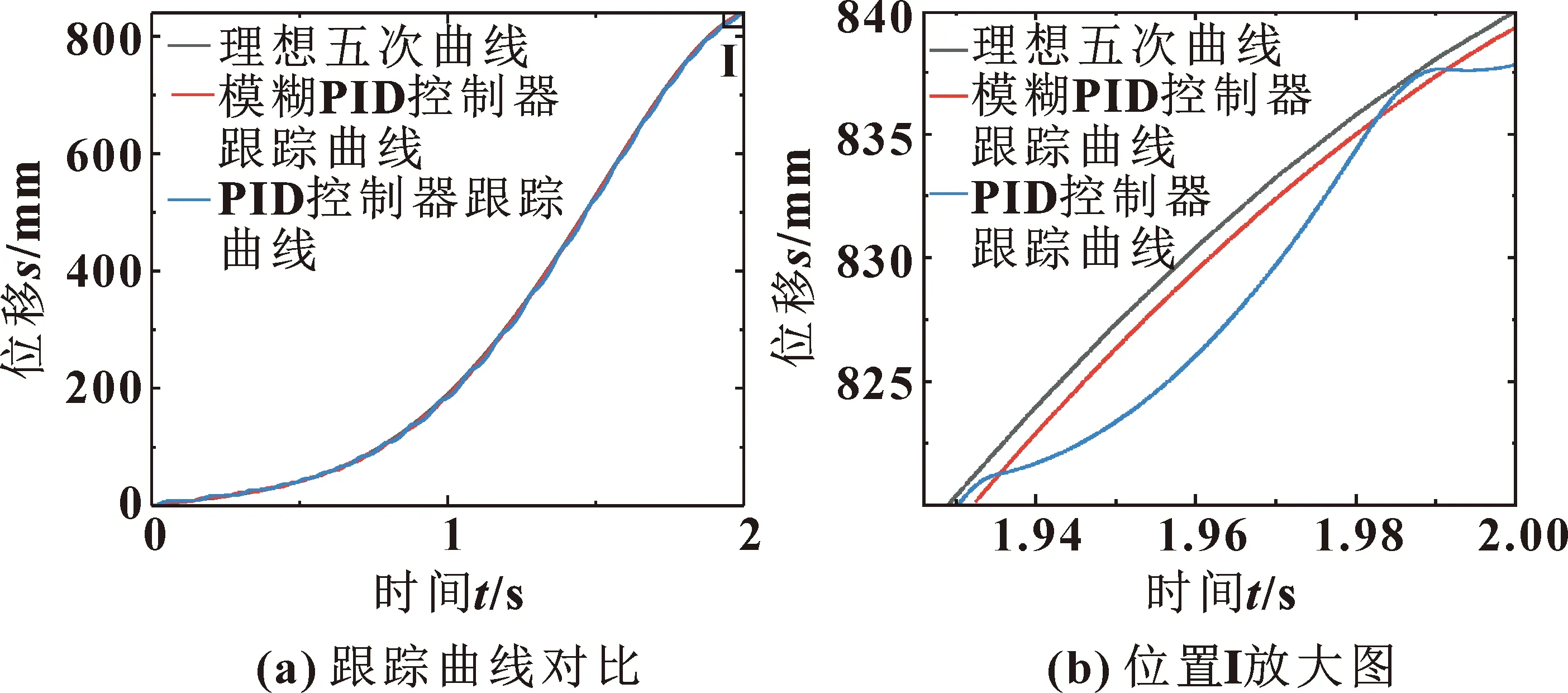
图7 仿真位移跟踪曲线

由图7可知：在1.94 s之后，模糊PID控制器系统下的仿真位移跟踪状态稳定。由图8可知：在1.4 s后，位移误差逐渐稳定。其中，PID控制器作用下的终止误差为2.18 mm，模糊PID控制器作用下的终止误差仅为0.66 mm。

图8 仿真过程位移误差对比

图9 仿真运动速度对比

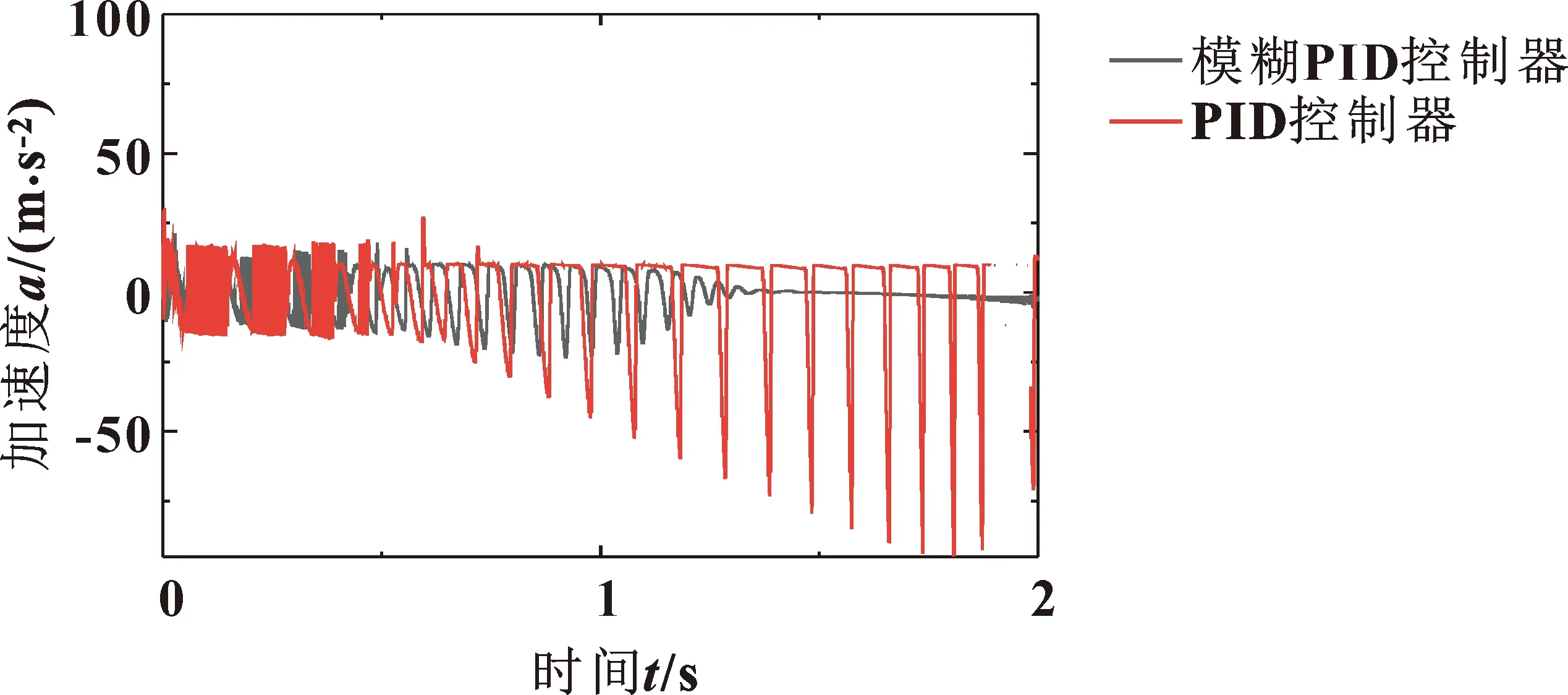
图10 仿真运动加速度对比

由图11知：活动横梁运动阶段，PID控制器方案中存在51.611 MPa的压力突变波动，而模糊PID控制器模型中压力波动最大仅为16.632 MPa。此外，1.4 s后模糊PID控制器模型下的压力值逐渐趋于平稳，PID控制器模型中的压力波动则逐渐加大震荡。

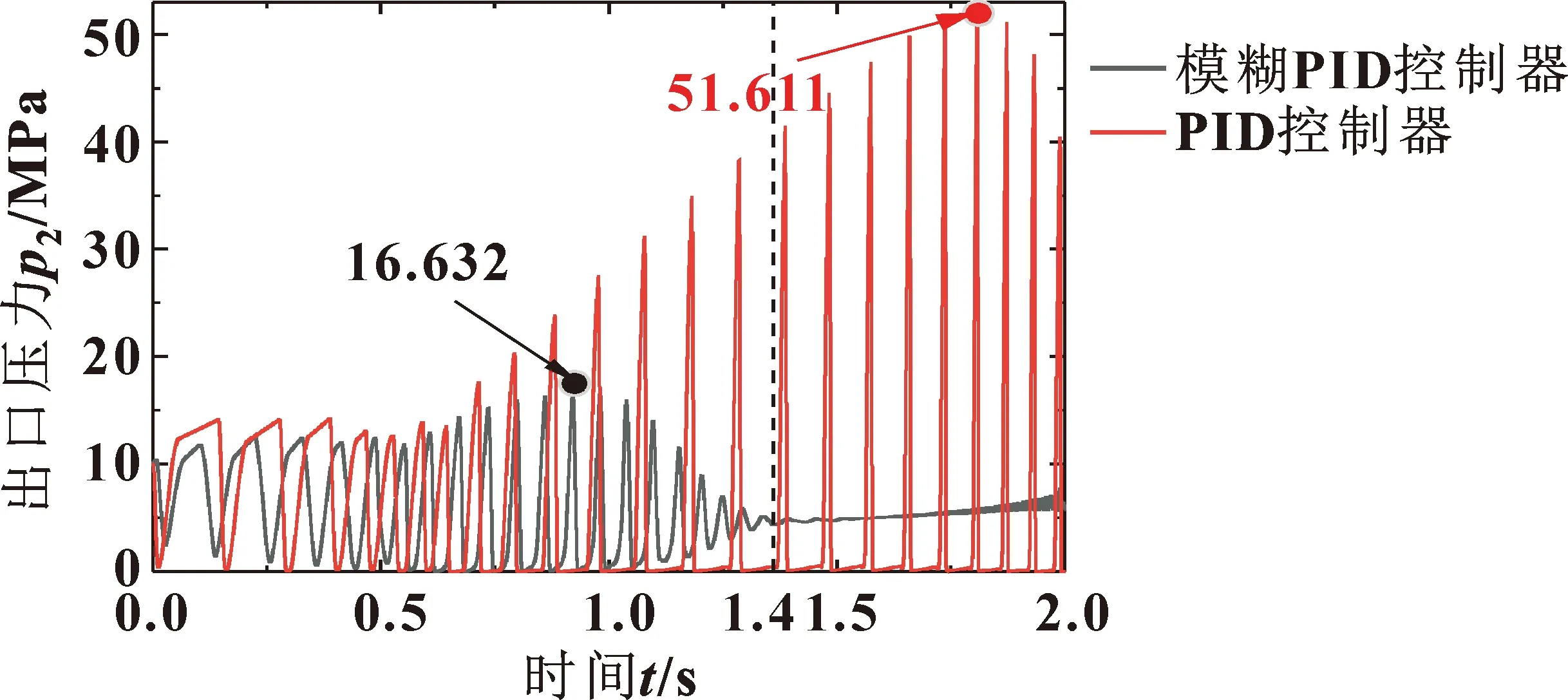
图11 仿真中出油口压力对比

3 实验验证

为了进一步验证优化后的五次运动曲线模型仿真分析的正确性和有效性，搭建了液压成形装备实验台，如图12所示，表3为液压元件及其相关参数。通过控制主缸，完成对理想五次运动曲线的跟踪。

表3 实验用液压元件型号

液压机还设置了压力传感器和速度传感器等。将传感器安装在液压机框架及回油路中，用于监控系统的运行状态。控制系统集成在电气柜和控制台中，主要由个人计算机、工控机、采集卡以及输出卡等组成。其中，个人计算机作为主控计算机通过网线与作为目标计算机的工控机进行TCP/IP数据交换。最后，在实验中设置PID和模糊PID控制系统对照组，分别应用于曲线的运动控制。

3.1 位移跟踪实验分析

实验结果如图13—17所示。实验选用2种控制方案分别匹配运动模型进行验证。

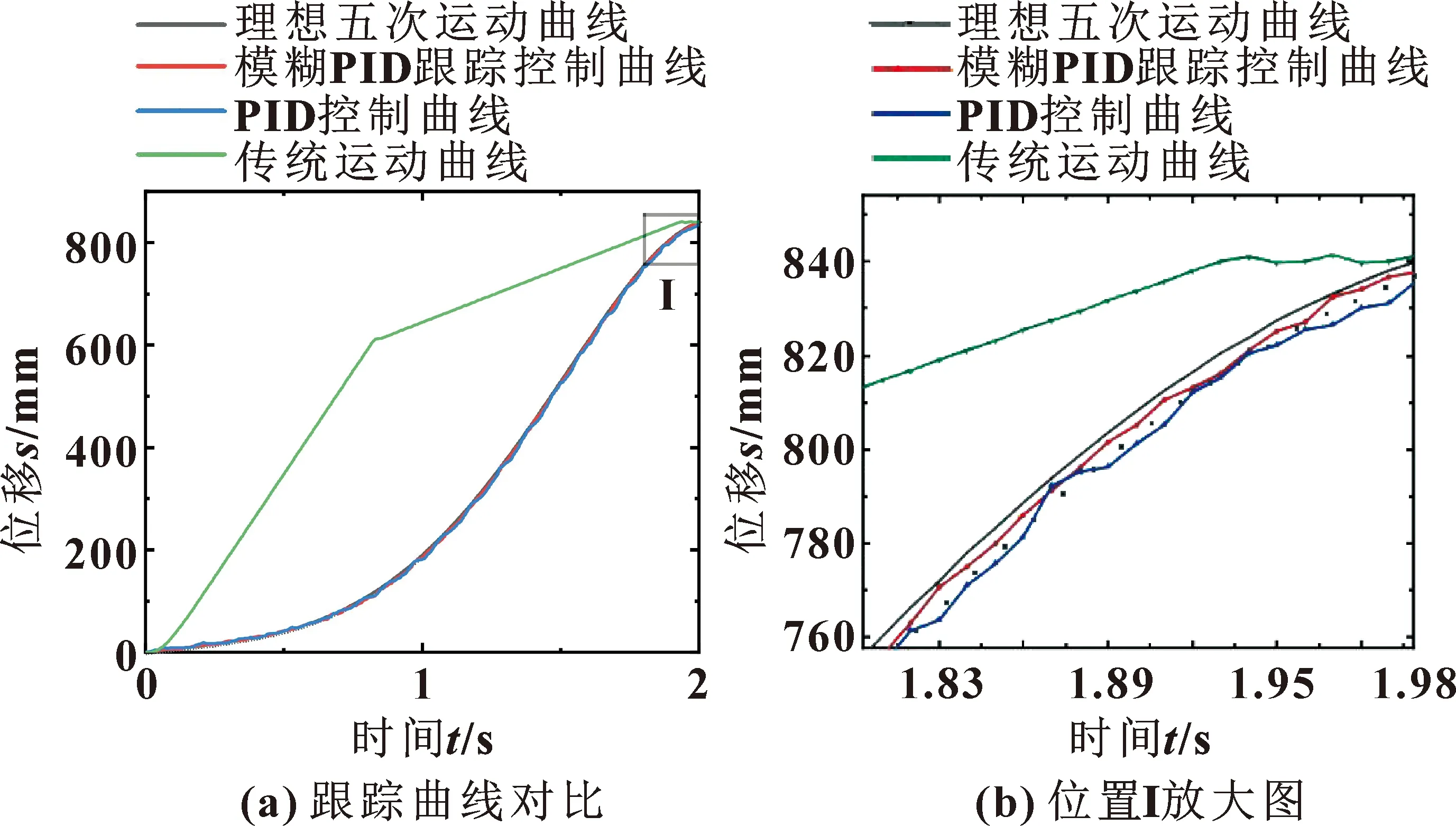
图13 实验位移跟踪曲线对比

由图14—16可知：在2种控制器模型下，活动横梁在0.8 s内都存在震荡现象。其中，模糊PID控制器下的误差在-2～1 mm内，PID控制器在此时间内的位移误差范围为-5～1 mm，存在较大的误差震荡。

图14 实验位移运动跟踪误差

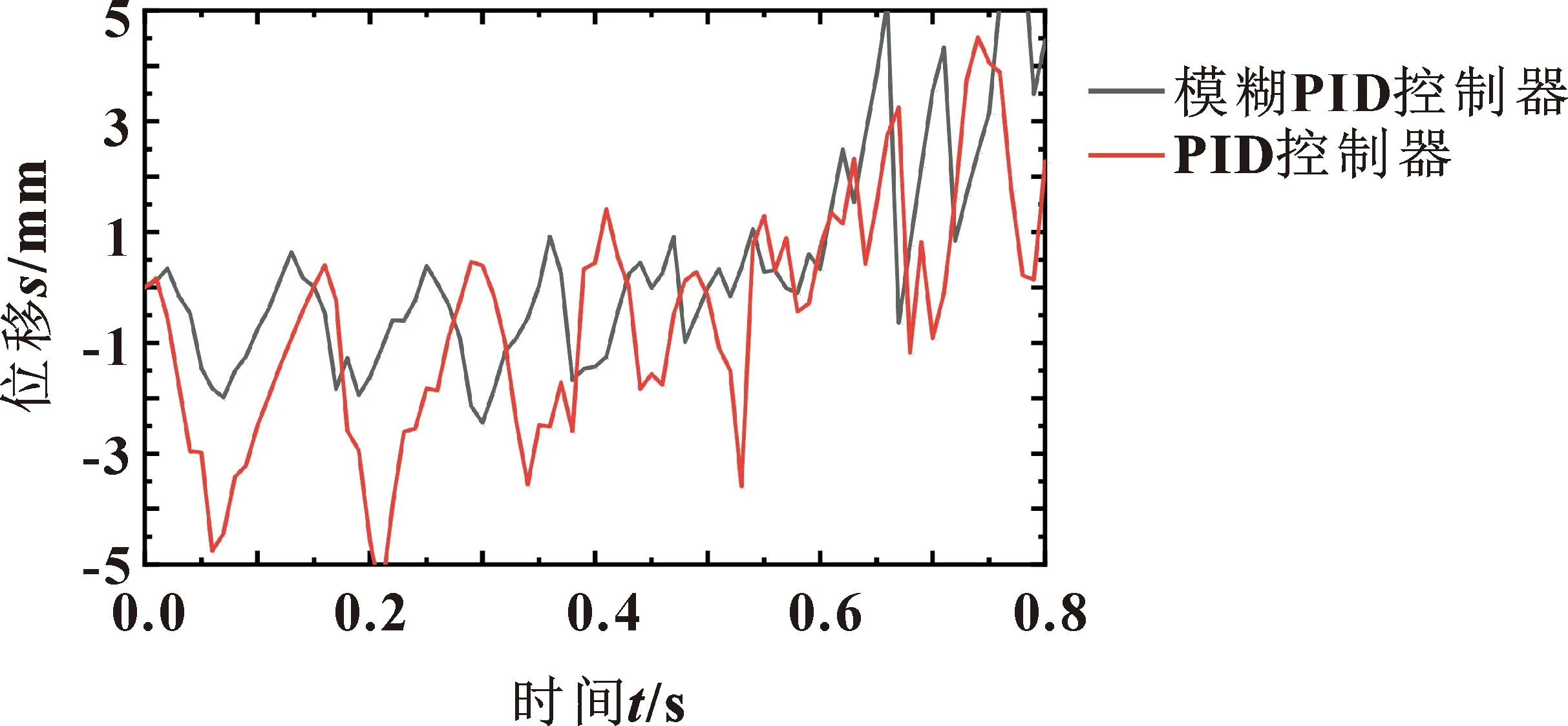
图15 图14中局部放大A

图16 图14中局部放大B

其次，0.8 s后在2种控制器作用下的实际位移曲线逐渐趋于平稳，模糊PID控制器位移终止误差仅为2.7 mm，PID控制器终止运动时的位移误差为4.02 mm。

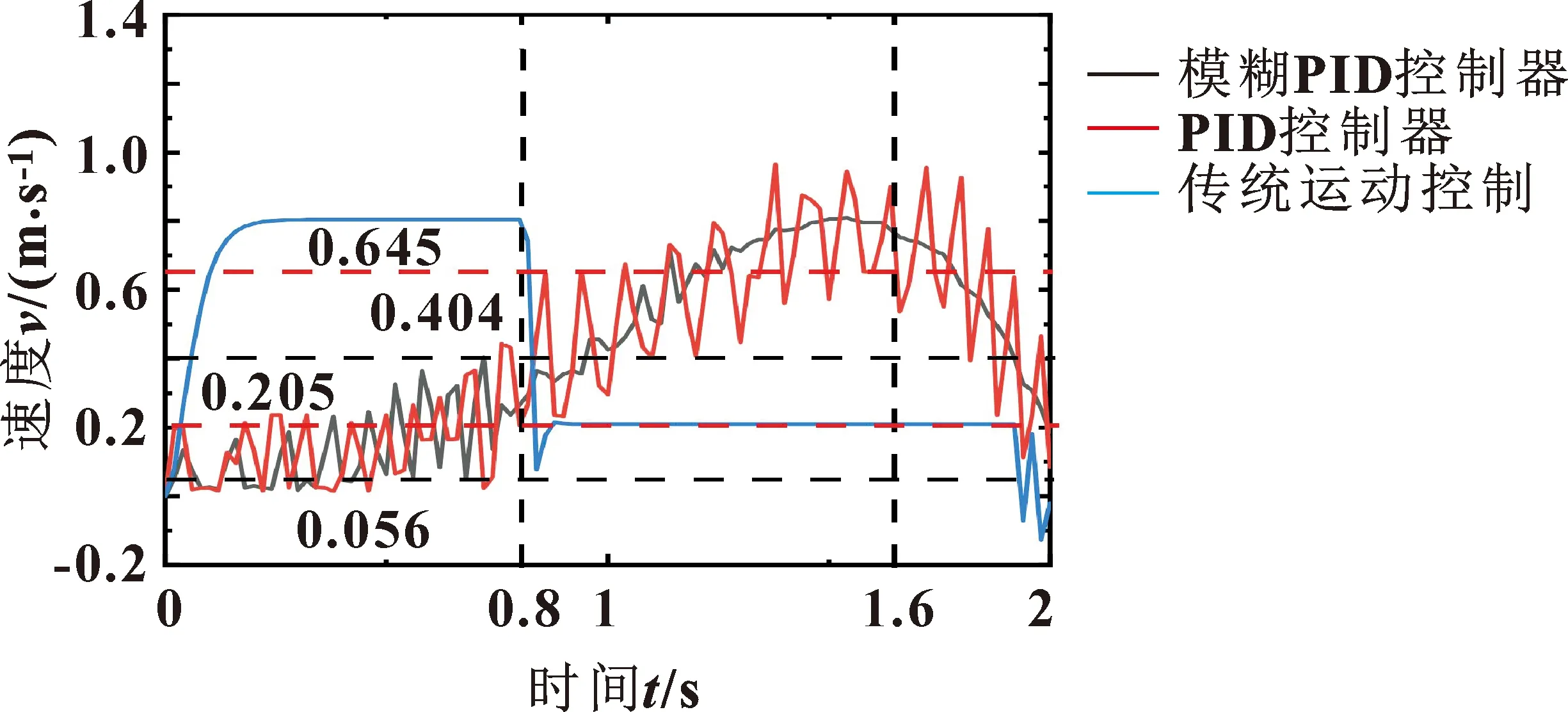
图17 实验运动速度曲线对比

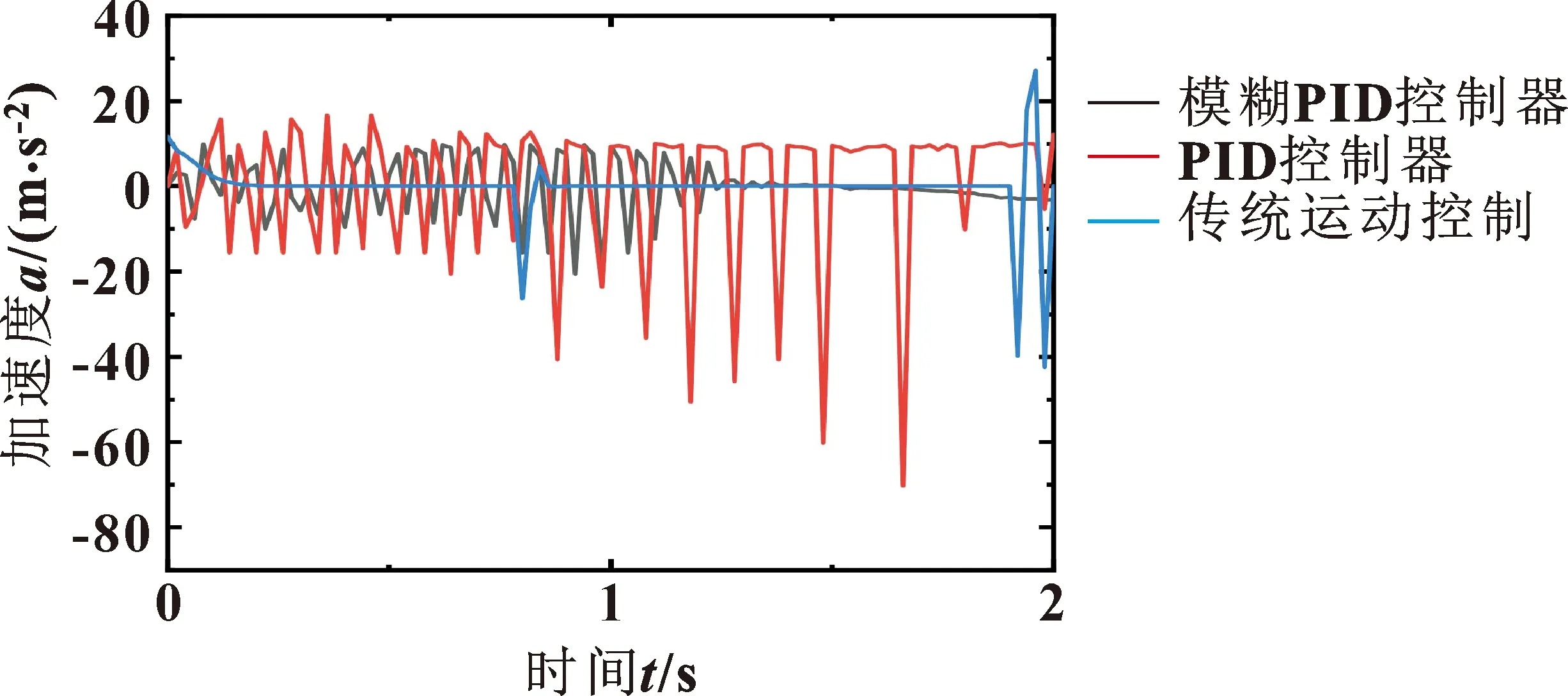
图18 实验运动加速度曲线对比

3.2 系统平稳性提升分析

通过仿真和实验分析可知，与传统的运动模型相比，优化后的五次多项式运动曲线较好地消除了运动过程中的速度突变问题。在活动横梁快速运动的过程中，该运动模型最大程度上消除了速度突变带来的冲击和振动问题。同时，工控机Simulink Realtime 平台在模糊PID控制器和高频响阀的配合下能够完成较好的生产应用，为更先进的控制算法应用提供基础。

3.3 控制器应用分析

如图13—16所示，在活动横梁运动过程中，0～0.8 s内，2种控制器作用下的运动都存在一定的波动。但是在模糊PID控制器的作用下，位移误差相对于PID控制器减小了1.95 mm。同时由图17—18可得：在模糊PID控制器模型下，活动横梁运动过程中无较大的速度拐点且1.6 s后运动速度能够稳定减小。

4 讨论

通过仿真和实验分析可知，模糊PID控制器能够解决活动横梁下降过程中的非线性冲击振动与位移误差的问题。但是，五次运动曲线是否能够应用于各种大型复合材料成形装备之中，仍然需要大量的实践应用，且在控制器应用之前，需要对模糊PID控制器的输入和输出模糊论域进行多次测试，从而找到合适的范围。

在未来的研究中，考虑将不同的具有平稳特性的曲线运用到优化模型之中，采用高性能的控制算法应用到成形装备控制过程，促进高速成形装备的产业化应用。

5 结论

为了解决活动横梁快降过程中的冲击和振动问题，提出了基于五次运动曲线的平稳性控制方法，仿真和实验结果均表明运动冲击和振动明显减小，可实现活动横梁无冲击的、高精度的非线性运动控制。在模糊PID控制器系统中，活动横梁位移跟踪误差为2.7 mm，最大速度冲击波动降低了21%，有效提升了装备服役过程的稳定性。

该设计能够对现有大型液压机的设计和平稳性控制提供有效参考，且经过不断的改进，能够满足更为苛刻的工艺要求，实现大型液压成形装备高精度和高稳定性能的提升。